三视图
- 格式:docx
- 大小:100.92 KB
- 文档页数:5





第8讲三视图,体积与表面积的计算[知识梳理]1.空间几何体的结构特征2.空间几何体的三视图1.多面体的表(侧)面积因为多面体的各个面都是平面,所以多面体的表面积就是所有侧面的面积之和,表面积是侧面积与底面面积之和.2.柱、锥、台和球的表面积和体积3.常见几何体的侧面展开图及侧面积题型一空间几何体的三视图(高频考点题,多角度突破)考向一已知几何体,识别三视图1.(东北四市联考)如图,在正方体ABCDA1B1C1C1中,P是线段CD的中点,则三棱锥PA1B1A的侧视图为()考向二已知三视图,判断几何体的形状2.一个几何体的三视图如图所示,则该几何体的直观图可以是()考向三已知三视图中的两个视图,判断第三个视图3.(石家庄质检)一个三棱锥的正视图和俯视图如图所示,则该棱锥的侧视图可能为()【针对补偿】1.(济南模拟)如图,多面体ABCDEFG的底面ABCD为正方形,FC=GD=2EA,其俯视图如图所示,则其正视图和侧视图正确的是()2.(北京)某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为()A.32B.2 3 C.22D.23.(南昌一模)如图,在正四棱柱ABCDA1B1C1D1中,点P是平面A1B1C1D1内一点,则三棱锥PBCD的正视图与侧视图的面积之比为()A.1∶1 B.2∶1 C.2∶3 D.3∶2[知识自测]1.将边长为1的正方形以其一边所在直线为旋转轴旋转一周,所得几何体的侧面积是( )A .4πB .3πC .2πD .π2.(全国甲卷)如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为( )A .20πB .24πC .28πD .32π3.正三棱柱ABC A 1B 1C 1的底面边长为2,侧棱长为3,D 为BC 中点,则三棱锥A B 1DC 1的体积为______.题型一 空间几何体的表面积与侧面积(基础拿分题,自主练透)(1)(课标Ⅰ)某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形,这些梯形的面积之和为( )A .10B .12C .14D .16(2)一个六棱锥的体积为23,其底面是边长为2的正六边形,侧棱长都相等,则该六棱锥的侧面积为______.【针对补偿】1.(全国Ⅰ卷)如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是283π,则它的表面积是( )A.17π B.18π C.20π D.28π2.(黑龙江省大庆中学期中)一个体积为123的正三棱柱的三视图如图所示,则这个三棱柱的侧视图的面积为()A.6 3 B.8 C.8 3 D.12题型二空间几何体的体积(高频考点题,多角突破)考向一求以三视图为背景的几何体的体积1.(课标Ⅱ)如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分所得,则该几何体的体积为()A.90π B.63π C.42π D.36π考向二不规则几何体的体积3.如图,在多面体ABCDEF中,已知ABCD是边长为1的正方形,且△ADE,△BCF 均为正三角形,EF∥AB,EF=2,则该多面体的体积为()A.23 B.33 C.43 D.32考向三 柱体与锥体的内接问题4.(2015·湖南卷)某工件的三视图如图所示,现将该工件通过切削,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为⎝ ⎛⎭⎪⎫材料利用率=新工件的体积原工件的体积( )A.89πB.827π C.24(2-1)3π D.8(2-1)3π【针对补偿】3.(新课标全国Ⅱ卷)如图,网格纸上正方形小格的边长为1(表示1 cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3 cm ,高为6 cm 的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为( )A.1727B.59C.1027D.134.(山东)由一个长方体和两个14圆柱体构成的几何体的三视图如下图,则该几何体的体积为______.题型三 球与几何体的切接问题 考向一 正方体(长方体)的外接球1.(天津)已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为18,则这个球的体积为______.考向二 直三棱柱的外接球2.已知直三棱柱ABC A 1B 1C 1的6个顶点都在球O 的球面上,若AB =3,AC =4,AB ⊥AC ,AA 1=12,则球O 的半径为( )A.3172 B .210 C.132D .310【针对补偿】5.(广州市综合测试)一个六棱柱的底面是正六边形,侧棱垂直于底面,所有棱的长都为1,顶点都在同一个球面上,则该球的体积为( )A .20π B.205π3C .5πD.55π6[A 基础巩固练]1.(浙江)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm 3)是( )A.π2+1B.π2+3C.3π2+1 D.3π2+3 2.(山西省高三考前质量检测)某几何体的三视图如图所示,若该几何体的体积为37,则侧视图中线段的长度x 的值是( )A.7 B .27 C .4D .53.(课标Ⅲ)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )A .π B.3π4 C.π2D.π45.某三棱锥的三视图如图所示,该三棱锥的表面积是( )A .28+6 5B .30+6 5C .56+12 5D .60+125。
三视图在设计和制造产品时,三视图是非常重要的工具。
它提供了产品的正面、侧面和顶面的视图,以便更好地理解产品的外观和尺寸。
三视图通常用于制造机械、汽车、建筑以及其他工业和工程领域中的产品设计。
什么是三视图?三视图是指一个物体或产品的正、侧、顶三个方向的视图。
每个视图展示物体或产品的不同面,以便观察和描述其外观和尺寸。
通过组合这些视图,我们可以获得一个全面的、立体感的理解。
三视图通常用于制图和设计中,以便准确地定义产品的形状和尺寸。
每个视图都是从不同的角度观察物体或产品,以确保从各个方向都可以得到必要的信息。
三视图的类型三视图通常包括正视图、侧视图和顶视图。
每个视图都提供了一个特定的角度和视角,以便全面了解产品的形状和结构。
正视图正视图是从产品的正面观察的视图。
它显示了产品的前方轮廓,包括外形和特征。
正视图是最常用的视图之一,因为它提供了产品最直观的外观。
侧视图侧视图是从产品的侧面观察的视图。
它显示了产品的侧面轮廓,包括任何突出部分、凹槽或其他重要特征。
侧视图提供了产品的横向尺寸和形状信息。
顶视图顶视图是从产品的上方观察的视图。
它显示了产品的上方轮廓,包括任何平面特征和凹槽。
顶视图通常用于确定产品的长度、宽度和高度。
三视图的重要性三视图对于产品的设计和制造非常重要。
它们提供了产品外观、尺寸和比例的信息,以便设计师和制造商能够准确地构建产品。
帮助设计与制造三视图是设计师和制造商之间进行沟通和理解的重要工具。
通过观察和分析三视图,设计师可以更好地理解产品的外观和尺寸,从而更好地进行设计和制造。
简化复杂性许多产品都具有复杂的形状和结构。
三视图可以将复杂的产品拆分为简单的部分和平面,从而使设计和制造变得更加简单和可行。
提供准确度和一致性三视图提供了准确的尺寸和比例,以便设计师和制造商可以按照相同的标准进行工作。
这确保了产品的一致性和质量。
三视图的制作制作三视图需要一些专业的工具和技能。
下面是一些常见的制作三视图的方法:手绘在计算机绘图软件出现之前,手绘是制作三视图的主要方式。
视图和三视图:
(1)视图:当我们从某个角度观察一个物体时,所看到的的图像叫做物体的一个视图。
视图也可以看做物体在某个角度的光线的投影,对于同一物体,如果从不同的角度观察,所得到的视图可能不同。
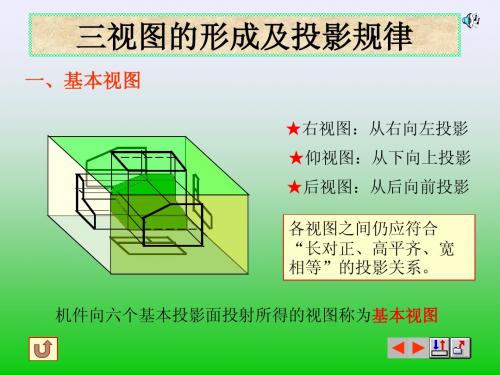
(2)三视图:一个物体在三个投影面(正面、侧面、水平面)内同时进行正投影,得到三种图形,叫做三视图。
主视图:在正面内得到的由前向后观察物体的视图,叫做主视图;俯视图:在水平面内得到的由上向下观察物体的视图,叫做俯视图;左视图:在侧面内得到的由左向右观察物体的视图,叫做左视图。
三视图中各种视图分别是从不同方向表示物体的,三者结合起来就能够较全面的反映物体的形状。
三视图反映物体的特征如下:
主视图反映几何体的长和高;
俯视图反映几何体的长和宽;
左视图反映几何体的宽和高。
常见几何体的三视图:
1、(2011四川达州,3,3分)如图是由几个相同的小正方体搭成的一个几何体,它的左视图是()
A、B、
C、D、
考点:简单组合体的三视图。
分析:根据左视图是从左面看到的图判定则可.
解答:解:左面看去得到的正方形从左往右依次是2,1,故选B.
点评:本题考查了几何体的三视图,从正面看到的图叫做主视图,从左面看到的图叫做左视图,从上面看到的图叫做俯视图.
n
2、(2011四川广安,9,3分)由个相同的小正方体堆成的几何体,其视图如下所示,则
的最大值是()
A .18
B .19
C .20
D .21
考点:三视图,由三视图确定物体的个数
专题:视图与投影
分析:综合主视图和俯视图,可知该几何体由三层组成,最底层最多有7个小正方体,第二层最多有7个小正方体,第三层最多有4个小正方体,故最大为7+7+4=18.
解答:A
点评:解决此类问题要具备空间想象能力,根据主视图与俯试图的形状来想象出几何体的组合方式,确定该物体的行数、列数和层数,确定出每层可能的最多小正方体的个数后即可判断.
3、(2011,四川乐山,4,3分)如图,在正方体ABCD ﹣A 1B 1C 1D 1中,E 、F 、G 分别是AB 、BB 1、BC 的中点,沿EG 、EF 、FG 将这个正方体切去一个角后,得到的几何体的俯视图是( )
A. B. C. D. 考点:简单组合体的三视图。
分析:找到从上面看所得到的图形即可,注意所有的看到的棱都应表现在俯视图中. 解答:解:从上面看易得1个正方形,但上面少了一个角,在俯视图中,右下角有一条线段.
故选B .
点评:本题考查了三视图的知识,主视图是从物体的正面看得到的视图.
n
n
4、(2011四川泸州,10,2分)如图是一些大小相同的小正方体组成的几何体的主视图和俯视图,则组成这个几何体的小正方体最多块数是()
A.8
B.10
C.12
D.14
考点:由三视图判断几何体.
分析:主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形,再根据主视图与俯视图得出答案。
解答:解:根据几何体的主视图和俯视图,可以得出从主视图看最少有6个,从俯视图看,最左边正方形前后可以有三列,分别有三个,故最多有3×3+3=12个,故选C.点评:此题主要考查了三视图的概念.根据从俯视图看,最左边正方形前后可以有三列,分别有三个从而得出答案是解决问题的关键.
5、由一些大小相同的小正方体搭成的几何体的俯视图如右图所示,其正方形中的数字表示该位置上的小正方体的个数,那么该几何体的主视图是()
A、B、C、D、
【答案】B
【考点】由三视图判断几何体;简单组合体的三视图.
【专题】几何图形问题.
【分析】俯视图中的每个数字是该位置小立方体的个数,分析其中的数字,得主视图有3列,从左到右分别是1,2,3个正方形.
【解答】解:由俯视图中的数字可得:主视图右3列,从左到右分别是1,2,3个正方形.故选B.
【点评】本题考查了学生的思考能力和对几何体三种视图的空间想象能力.注意找到该几何体的主视图中每列小正方体最多的个数.
6、(2011.四川雅安,4,3分)由四个大小相同的正方体组成的几何体如图所示,那么它的
D
C B A 俯视图是( )
A B C D
考点:简单组合体的三视图。
分析:根据题意,先理解给出的几何体的三视图是怎样的,利用空间想象能力易解答. 解答:解:该几何体由四个小正方体组成,第一行有3个小正方体,故它的俯视图为B .故选B .
点评:首先分清楚几何体由几个正方体组成,然后分清楚它的三视图,继而求解.
7、(2011四川省宜宾市,6,3分)如图所示的几何体的正视图是( )
考点:简单组合体的三视图.
分析:找到从正面看所得到的图形即可,注意所有的看到的棱都应表现在主视图中 答案:解:从正面看易得第一层有1个正方形,在右面,第二层有2个正方形, 故选:D .
点评:此题主要考查了三视图的知识,主视图是从物体的正面看得到的视图.
8、(2011成都,2,3分)如图所示的几何体的俯视图是( )
A .
B .
C .
D .
考点:简单几何体的三视图。
专题:应用题。
分析:题干图片为圆柱,主视图.左视图.俯视图是分别从物体正面.左面和上面看,所得到的图形.
解答:解:圆柱的主视图为长方形,左视图为长方形,俯视图为圆形.
故选D.
点评:本题考查了圆柱体的三视图,考查了学生的空间想象能了及解决问题的能力.。