- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
D.200π cm2
高频考向探究
【方法模型】 由几何体的三视图求几何体的侧面积、体积等问题,关键是由三视图抽象出几何体的形状,然后
再进行相关计算.
高频考向探究
针对训练 [2018·莱芜] 已知圆锥的三视图如图 30-20 所示,则这个圆锥的侧 面展开图的面积为 ( )
[答案] B
[解析] 因为圆锥的侧面展开图是扇形,
课前双基巩固
考点三 直棱柱的展开与折叠
1.[2018·天门] 如图 30-5 是某个几何体的展开图,该几何体是 ( A )
A.三棱柱 C.圆柱
B.三棱锥 D.圆锥
图 30-5
课前双基巩固
2.如图 30-6 是一个长方体包装盒,则它的表面展开图是 ( A )
图 30-6
图 30-7
课前双基巩固
知识梳理 几何体 直三棱柱 直四棱柱
A.3 个
B.4 个
C.6 个
D.9 个
[答案] B [解析] 由俯视图易得最底层有 3 个立 方体,第二层有 1 个立方体,故组成该
几何体的小立方体c有 3+1=4(个).
图 30-16
图 30-17
高频考向探究
针对训练
1.[2018·丽水] 一个几何体的三视图如图 30-17 所示,该几何体是 ( A )
图 30-12
图 30-13
2.[2018·绍兴] 由 6 个相同的立方体搭成的几何体如图 30-14 所示,则它的主视图是 ( D )
图 30-14
图 30-15
高频考向探究
探究三 由视图确定几何体
例 3 [2018·青海] 如图 30-16 是由一些相同小立方体搭成的几何
体的三视图,则搭成该几何体的小立方体有 ( )
A.圆柱 C.长方体
B.圆锥 D.球
图 30-21
当堂效果检测
2.[2018·宁波] 如图 30-22 是由 6 个大小相同的立方体组成的几何体,在这个几何体的三视图中是中心对称
图形的是 ( C )
A.主视图
B.左视图
C.俯视图
D.主视图和左视图
图 30-22
当堂效果检测
3.[2018·安徽] 一个由圆柱和圆锥组成的几何体如图 30-23 水平放置,其主(正)视图为( A )
“前”字对面的字c为“真”.
图 30-8
A.认
B.真
C.复
D.习
高频考向探究
针对训练 如图 30-9①是由边长为 1 的六个小正方形组成的图形,它可以围成如图②所示的正方体,则图中小正方形顶 点 A,B 在围成的正方体上的距离是( B )
A.0 C. 2
B.1 D. 3
图 30-9
Hale Waihona Puke 高频考向探究探究二 几何体的三视图
图 30-1 D.八棱柱
课前双基巩固
知识梳理
多面体
由若干个平面围成的几何体
(1)上、下两个底面彼此 全等 ;
直
特征
(2)侧面的形状都是 矩形 ;
棱
(3)所有侧棱平行且 相等
柱
面、棱、顶点数 直 n 棱柱有 (n+2) 个面、 3n 条棱、 2n
个顶点
课前双基巩固
考点二 三视图
1.[2018·海南] 下列四个几何体中,主视图为圆的是 ( C )
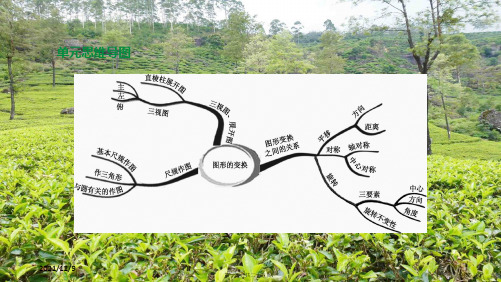
单元思维导图
第 30 课时 三视图与展开图
课前双基巩固
考点一 直棱柱
如果一个多面体的一个面是多边形,其余各面是有一个公共顶点的三角形,那么这个多面体叫做棱锥.如图 30-1 是一个四棱柱和一个六棱锥,它们各有 12 条棱,下列棱柱中和九棱锥的棱数相等的是 ( B )
A.五棱柱
B.六棱柱
C.七棱柱
先求得圆锥的母线长
l= 122 + 52=13(cmc),再根据扇形的面
积公式 S 扇形=12×10π×13=65π(cm2).
A.60π cm2 C.120π cm2
图 30-20 B.65π cm2 D.130π cm2
当堂效果检测
1.[2018·宜宾] 一个立体图形的三视图如图 30-21 所示,则该立体图形是( A )
体的三视图,则该几何体的侧面积是 ( )
[解析] 由题可知,此几何体是圆柱体,
所以该几何体的侧面展开图是一个长
方形,由比例可知底c面半径为 5 cm,高
图 30-19
为 20 cm,所以 S 侧 =2πr×h=2π×5×20=200π(cm2).
A.200 cm2
B.600 cm2
C.100π cm2
图 30-2
课前双基巩固
2.[2018·齐齐哈尔] 如图 30-3 所示的三棱柱的三视图如图 30-4 所 [答案] 4 2
示,已知△EFG 中,EF=8 cm,EG=12 cm,∠EFG=45°,则 AB 的长为 [解析] 由三视图的性质可知,△EFG 中,
cm.
边 FG 上的高等于 AB 的长,∵EF=8,
A.直三棱柱
B.长方体
C.圆锥
D.立方体
图 30-18
高频考向探究
2.[2017·常州] 如图 30-18 是某个几何体的三视图,则该几何体是 [答案] B
()
[解析] 由俯视图知是三棱柱或三棱锥,
A.圆锥 B.三棱柱
再由主视图排除三棱锥.
c
C.圆柱
D.三棱锥
高频考向探究
探究四 有关视图的计算
例 4 [2017·湖州] 如图 30-19 是按 1∶10 的比例画出的一个几何 [答案] D
图 30-23
图 30-24
4.[2018·无锡] 下面每个图形都是由 6 个边长相同的正方形拼成的图形,其中能折叠成正方体的是 ( C )
例 2 [2018·湖州] 如图 30-10 所示的几何体的左视图是 ( D )
图 30-10
图 30-11
【方法模型】判断几何体的三视图,关键是先分清每个视图观察的方向,然后想象看到的图形的形状.
高频考向探究
针对训练 1.[2018·温州] 移动台阶如图 30-12 所示,它的主视图是 ( B )
正方体 直 n 棱柱
展开图
底面形状 三角形 四边形 正方形 多边形
侧面形状 矩形 矩形
正方形 矩形
高频考向探究
探究一 直棱柱的展开图
例 1 [2018·内江] 如图 30-8 是正方体的表面展开图,则与“前” 字相对的字是 ( )
[答案] B [解析] 正方体的展开图中,相隔一个面 的平面在正方体的相对面的位置,所以
∠EFG=45°,∴AB=8c×sin45°=4 2.
图 30-3
图 30-4
课前双基巩固
知识梳理 1.三视图
主视图:从 前面 看到的图 左视图:从 左面 看到的图 俯视图:从 上面 看到的图 2.在画几何体的三视图时,应注意以下两点: (1)长 对正 、高 平齐 、宽 相等 ; (2)图中看不到的棱应用虚线表示出来.