正方体的平面展开图及三视图练习知识讲解
- 格式:doc
- 大小:386.51 KB
- 文档页数:5
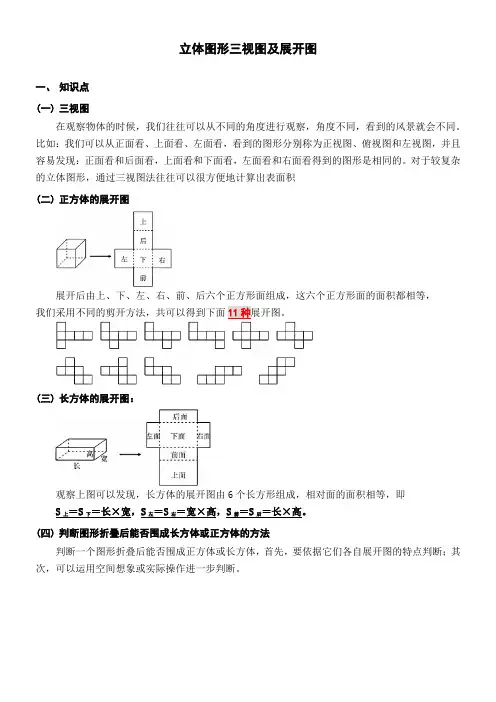
立体图形三视图及展开图一、知识点(一)三视图在观察物体的时候,我们往往可以从不同的角度进行观察,角度不同,看到的风景就会不同。
比如:我们可以从正面看、上面看、左面看,看到的图形分别称为正视图、俯视图和左视图,并且容易发现:正面看和后面看,上面看和下面看,左面看和右面看得到的图形是相同的。
对于较复杂的立体图形,通过三视图法往往可以很方便地计算出表面积(二)正方体的展开图展开后由上、下、左、右、前、后六个正方形面组成,这六个正方形面的面积都相等,我们采用不同的剪开方法,共可以得到下面(三)长方体的展开图:观察上图可以发现,长方体的展开图由6个长方形组成,相对面的面积相等,即S上=S下=长×宽,S左=S右=宽×高,S前=S后=长×高。
(四)判断图形折叠后能否围成长方体或正方体的方法判断一个图形折叠后能否围成正方体或长方体,首先,要依据它们各自展开图的特点判断;其次,可以运用空间想象或实际操作进一步判断。
二、题型(一)展开图与对立面【例1.1】水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示,如下图,是一个正方体的平面展开图,若图中的“似”表示正方体的前面,“锦”表示右面,“程”表示下面。
则“祝”、“你”、“前”分别表示正方体的________________________。
【答案】后面、上面、左面【解析】易知“你”、“程”相对,“前”、“锦”相对,“祝”、“似”相对,因此“祝”、“你”、“前”分别表示正方体的后面、上面、左面。
【例1.2】一个数学玩具的包装盒是正方体,其表面展开图如下。
现在每方格内都填上相应的数字。
已知将这个表面展开图沿虚线折成正方体后,相对面的两数之和为“3”,则填在A、B、C内的三个数字依次是___________。
【答案】3、1、2【解析】面上的数是“0”,与“B”相对的面上的数是“2”,与“C"相对的面上的数是“1”。




正方体的11种展开图打印附带讲解本文章主要带孩子认识11种正方体展开图,家人可以把它打印下来,陪孩子一起制作。
(PS:1、如果A4的纸太软不好固定,可以用纸箱、纸质购物袋等画出对应的图形进行裁剪;2、亦或者可以用包书的纸裁剪出展开图的样子,做成精美的包装纸贴在正方体外面,做一个精美的小礼盒哦)(为了方便打印,文章末尾,把所有资料汇总了一遍,可直接跳转到末尾打印11钟展开图)在正式学习之前,可以将家中的魔方拿出来,看看正方体有几面?每一面都是什么形状?以此区分一下正方体和正方形。
分别有前面、后面、上面、下面、左面、右面这六面。
接着介绍“正方体的展开图”,带着孩子观察展开图的特点,并知道其名称。
(一)首先认识一下1-4-1型,为了更形象的记忆,我把它概括为“1头4身体1脚”(头是由1个正方形组成的,身体是由4个正方形组成的,脚是由1个正方形组成的,)家人可以先把图形制作出来,然后带孩子去观察特点。
打印图纸:1-4-1打印专用:1-4-1共有6种,身体均是4个正方体,头和脚各一个,头和脚的位置可左右移动改变(二)接下来认识2-3-1型,2-3-1共有3种,头2个正方体,身体3个,脚1个。
脚的位置可左右移动改变,以此展开图为例,虽然身体部分较原来少了一个,但是恰好可以由头部多的一个补上。
操作演示时,先把身体折起来,发现身体少了一个,接着把上面脑袋部分拼好,拼好之后脑袋部分多的一个刚好可以补充身体。
2-3-1打印专用:2-3-1共有3种,头2个正方体,身体3个,脚1个。
脚的位置可左右移动改变(三)接下来认识2-2-2型,与3-3型,可以把资料打印下来,通过操作去提升动手以及想象能力。
2-2-2与3-3打印专用。

正方体展开图和三视图的初步认识1.认识立体图形和平面图形我们常见的立体图形有长方体、正方体、球、圆柱、圆锥,此外,棱柱,棱锥也是常见的几何体。
我们常见的平面图形有正方形、长方形、三角形、圆2. 立体图形和平面图形关系立体图形问题常常转化为平面图形来研究,常常会采用下面的作法(1)画出立体图形的三视图立体图形的的三视图是指正视图(从正面看)、左视图(从左面看)、俯视图(从上面看)得到的三个平面图形。
(2)立体图形的平面展开图常见立体图形的平面展开图圆柱、圆锥、三棱柱、三棱锥、正方体(共十一种)知识梳理知识梳理1 正方体的侧面展开图(共十一种)分类记忆:第一类,中间四连方,两侧各一个,共六种。
第二类,中间三连方,两侧各有一、二个,共三种。
第三类,中间二连方,两侧各有二个,只有一种。
第四类,两排各三个,只有一种。
知识梳理2 常见立体图形的平面展开图1. 棱柱:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱。
两个互相平行的平面叫做棱柱的底面,其余各面叫做棱柱的侧面。
两个侧面的公共边叫做棱柱的侧棱。
侧面与底的公共顶点叫做棱柱的顶点,不在同一个面上的两个顶点的连线叫做棱柱的对角线,两个底面的距离叫做棱柱的高。
棱柱的底面可以是三角形,四边形,五边形……我们把这样的棱柱叫分别叫做三棱柱、四棱柱、五棱柱……棱柱的表面展开图是两个完全相同的多边形(作底面)和几个长方形(作侧面)2. 棱锥:一般地,有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥。
棱锥中的多边形叫做棱锥的底面。
棱锥中除底面以外的各个面都叫做棱锥的侧面。
相邻侧面的公共边叫做棱锥的侧棱。
棱锥中各个侧面的公共顶点叫做棱锥的顶点。
棱锥的顶点到底面的距离叫做棱锥的高。
棱锥中过不相邻的两条侧棱的截面叫做对角面。
棱锥的底面可以是三角形、四边形、五边形……我们把这样的棱锥分别叫做三棱锥、四棱锥、五棱锥……棱锥的展开图是由一个多边形(作底)和几个三角形(作侧面)组成的。

三视图和展开图的认识1.定义:三视图是指一个物体在三个不同方向上的投影,包括正视图、俯视图和侧视图。
2.作用:通过三视图可以全面了解物体的形状和结构,是工程制图和建筑设计中必不可少的一部分。
3.绘制方法:(1)正视图:物体正面朝向观察者,投影在水平面上。
(2)俯视图:物体上方朝向观察者,投影在垂直于水平面的竖直面上。
(3)侧视图:物体左侧或右侧朝向观察者,投影在垂直于水平面和俯视图所在平面的斜面上。
4.定义:展开图是将一个立体图形展开成平面图形,以便于观察和计算。
(1)矩形展开图:最常见的展开图类型,适用于各种矩形容器、包装盒等。
(2)圆形展开图:适用于圆形或近似圆形的物体,如圆筒、圆盘等。
(3)三角形展开图:适用于三角形的物体,如三角尺、三角形的包装盒等。
(4)其他多边形展开图:适用于各种多边形的物体,如六边形、八边形等。
5.绘制方法:(1)矩形展开图:将立体图形的侧面沿着高展开,得到一个长方形或正方形。
(2)圆形展开图:将立体图形的侧面沿着直径展开,得到一个扇形。
(3)三角形展开图:将立体图形的侧面沿着高展开,得到一个三角形。
(4)其他多边形展开图:根据立体图形的形状和结构,选择合适的方法将其展开。
三、三视图与展开图的相互关系1.展开图可以转化为三视图:通过观察展开图,可以确定物体的正视图、俯视图和侧视图。
2.三视图可以转化为展开图:根据三视图,可以绘制出物体的展开图。
3.展开图中的信息可用于三视图的绘制:展开图中的边长、角度等信息可以用于确定三视图中的尺寸和形状。
四、实际应用1.工程制图:在建筑设计、机械设计等领域,三视图和展开图是表达物体形状和结构的重要手段。
2.制造业:在制造过程中,通过三视图和展开图可以方便地切割、加工和组装物体。
3.教育:在三视图和展开图的教学中,有助于培养学生的空间想象能力和逻辑思维能力。
4.日常生活中:展开图在包装、折叠等方面有广泛应用,如纸箱、衣物等。
五、注意事项1.准确绘制:在绘制三视图和展开图时,要注意尺寸、形状和位置的准确性。
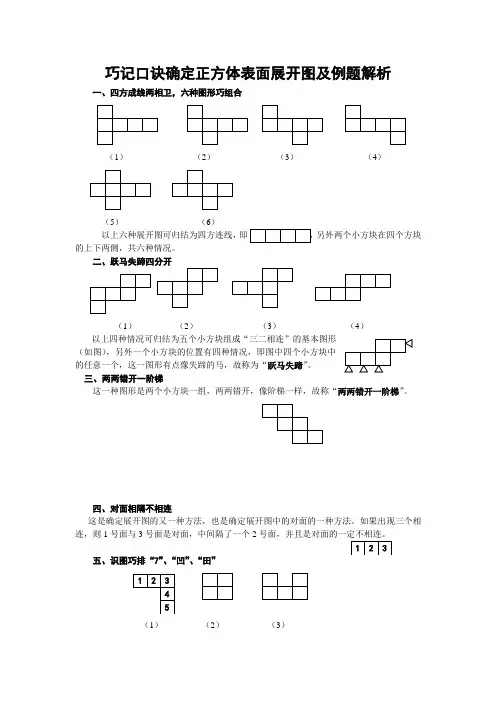
巧记口诀确定正方体表面展开图及例题解析一、四方成线两相卫,六种图形巧组合(1) (2) (3) (4)(5) (6)以上六种展开图可归结为四方连线,即另外两个小方块在四个方块的上下两侧,共六种情况。
二、跃马失蹄四分开(1) (2) (3) (4)以上四种情况可归结为五个小方块组成“三二相连”的基本图形(如图),另外一个小方块的位置有四种情况,即图中四个小方块中的任意一个,这一图形有点像失蹄的马,故称为“跃马失蹄”。
三、两两错开一阶梯这一种图形是两个小方块一组,两两错开,像阶梯一样,故称“两两错开一阶梯”。
四、对面相隔不相连这是确定展开图的又一种方法,也是确定展开图中的对面的一种方法。
如果出现三个相连,则1号面与3号面是对面,中间隔了一个2号面,并且是对面的一定不相连。
五、识图巧排“7”、“凹”、“田”(1) (2) (3)这里介绍的是一种排除法。
如果图中出现象图(1)中的“7”形结构的图形不可能是正方体展开图的,因为图中1号面与3号面是对面,3号面又与5号面是对面,出现矛盾。
如果图中出现象图(2)中的“田”形结构的图形不可能是正方体展开图的,因为同一顶点处不可能出现四个面的。
如果图中出现象图(3)中的“凹”形结构的图形不可能是正方体展开图的,因为如果把该图形折叠起来将有两个面重合。
现举例说明:例1.(2004海口市实验区)下面的平面图形中,是正方体的平面展开图的是()解析:本题可用“识图巧排‘7’、‘田’、‘凹’”来解决。
A、D都有“凹”形结构,B 有“田”形结构,故应选C例2.(2004扬州)马小虎准备制作一个封闭的正方体盒子,他先用5个大小一样的正方形制成如右图所示的拼接图形(实线部分),经折叠后发现还少一个面,请你在右图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.(注:①只需添加一个符合要求的正方形;②添加的正方形用阴影表示.)解析:本题可用“跃马失蹄四分开”来解决。


[]第14期方法与技巧]正方体的平面展开与折叠张奎甲山东省无棣县小泊头镇中学邮编:251911正方体的平面展开与折叠问题是初中数学的一个难点。
正方体的展开与折叠有助于培养学生对平面图形与空间几何体的相互转换的认识和空间想像能力,因此与正方体展开与折叠有关的试题成了中考的一个热点。
解决这类问题的方法主要有两种,一是通过动手操作来得到答案;二是通过分析正方体的结构特征,根据其平面展开图的内在规律得出结论。
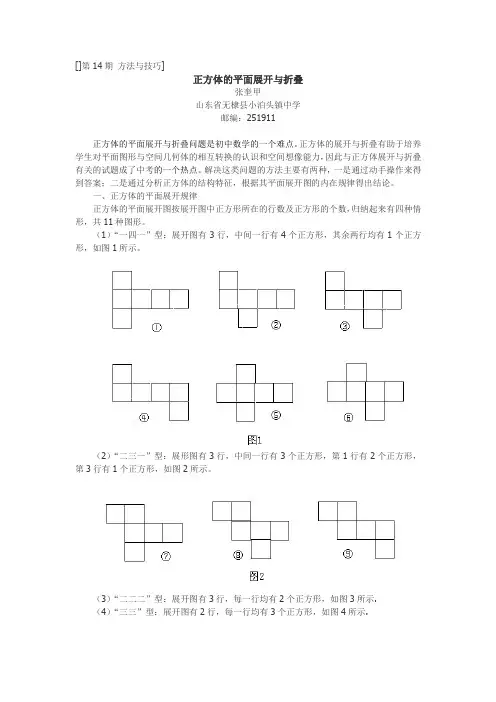
一、正方体的平面展开规律正方体的平面展开图按展开图中正方形所在的行数及正方形的个数,归纳起来有四种情形,共11种图形。
(1)“一四一”型:展开图有3行,中间一行有4个正方形,其余两行均有1个正方形,如图1所示。
(2)“二三一”型:展形图有3行,中间一行有3个正方形,第1行有2个正方形,第3行有1个正方形,如图2所示。
(3)“二二二”型:展开图有3行,每一行均有2个正方形,如图3所示.(4)“三三”型:展开图有2行,每一行均有3个正方形,如图4所示.以上是正方体平面展开图的几种形式.为方面记忆,总结口诀如下:中间四个面,上、下各一面;中间三个面,一、二隔河见;中间两个面,楼梯天天见;中间没有面,三、三连一线。
从图形我们可以看出如下规律:(1)每一个顶点至多有3个邻面,不会有4个或更多个.所以不存在“田”、“凹”、“凸”形排列;(2)“一”形排列的三个面中,两端的面一定是对面;(3)“L”形排列的三个面中,没有对面,只有邻面.二、正方体的折叠规律正方体的折叠规律与正方体的平面展开规律类似。
为方便起见,多采用填写字母的方式来确定所给图形能否折成正方体。
例如:图5中的4个图形都能折成正方体。
但图6的2个图形却不能围成正方体。
从图5、图6可以看出,由小正方形折叠成正方体,除正方体展开图规律外,还必须满足:(1)图形中要存在2A,2B,2C的条件;(2)相同字母不能在其他四个面的同列.。
正方体的11种平面展开图
正方体的平面展开图共有11种(那些经旋转或翻转后方向不同但实质相同的图形不重复计算),具体来讲分以下4类。
口诀:需背诵
正方体:中间四个面,上下各一面(6种摆法-141)
中间三个面,一二隔河见(3种摆法-132/231)
中间二个面,楼梯天天见(1种摆法-222)
中间没有面,三三连一线(1种摆法-33)
“田”“凹”应弃之
第一类:“1—4—1”型,其特点是有4个连成一排的正方形,两侧又各有1个正方形,共有6种。
口诀:中间四个面,上下各一面(上下面随便放)
第二类:“1—3—2”型,其特点是有3个连成一排的正方形,这一排正方形的一侧有1个正方形,另一侧有2个正方形(其中只有1个与中间那一排相连),共有3种。
口诀:中间三个面,一二隔河见(二三位置是固定的)
第三类:“2—2—2”型,其特点是有2个连成一排的正方形,其两侧又各有2个连成一排的正方形,只有1种。
口诀:中间二个面,楼梯天天见
第四类:“3—3”型,其特点是有3个连成一排的正方形,其一侧还有3个连成一排的正方形,只有1种。
中间没有面,三三连一线(1种摆法-33)。
正⽅体的平⾯展开图及三视图练习知识讲解正⽅体的平⾯展开图的判断问题题⽬特点:选择题,给出正⽅体相邻的三个⾯,并且三个⾯上分别标有不同的图案,要求判断其平⾯展开图是哪⼀个。
解题⽅法:排除法。
先看选择项中标有图案的⾯是否相对,若相对,排除。
然后注意到带图案的三个⾯有⼀个公共点,在原图和展开图上标出这个公共点。
最后,将其中的两个折叠后复原(如前⾯的⾯和上边的⾯),看另⼀个⾯是否符合,找出正确的答案。
注意:做题时,可将试卷旋转或颠倒⼀下判断,也可动⼿实际操作⼀下。
1.右⾯这个⼏何体的展开图形是()2.如图⼏何体的展开图形最有可能是()A、B、C、D、3.如图所⽰的正⽅体,若将它展开,可以是下列图形中的()A、B、C、D、4.如图所⽰的⽴⽅体,将其展开得到的图形是()A、B、C、D、5.四个图形是如图的展开图的是()A、B、C、D、6.如左图所⽰的正⽅体沿某些棱展开后,能得到的图形是()A、B、C、D、A B C D7.将如图所⽰表⾯带有图案的正⽅体沿某些棱展开后,得到的图形是()A、B、C、D、8.⼀个三⾯带有标记的正⽅体,如果把它展开,应是下列展开图形中的()A、B、C、D、9.下图右边四个图形中,哪个是左边⽴体图形的展开图?()A、B、C、D、10.如图,有⼀个正⽅体纸盒,在它的三个侧⾯分别画有三⾓形、正⽅形和圆,现⽤⼀把剪⼑沿着它的棱剪开成⼀个平⾯图形,则展开图可以是()A、B、C、D、11.将如图正⽅体的相邻两⾯上各画分成九个全等的⼩正⽅形,并分别标上O、×两符号.若下列有⼀图形为此正⽅体的展开图,则此图为()A、B、C、D、1.下⾯简单⼏何体的左视图是( ).2.如图所⽰,右⾯⽔杯的俯视图是( )A.B.C.D.正⾯321213、如图(1)放置的⼀个机器零件,若从正⾯看是如图(2),则其左⾯看是() 4. 若右图是某⼏何体的三种不同⽅向的图,则这个⼏何体是( )A.圆柱B.正⽅体C.球D.圆锥5. 图所⽰的物体,从左⾯看得到的图是()6、如图所⽰是由四个相同的⼩正⽅体组成的⽴体图形,它的俯视图为()7、如图2,这是⼀个正三棱柱,则从上⾯看到的图为()8、如图是由七个相同的⼩正⽅体堆成的物体,从上⾯看这个物体的图是()9、如图:是由⼏个⼩⽴⽅块搭成的⼏何体的俯视图,⼩正⽅形中的数字表⽰该位置⼩⽴⽅块的个数。
一、正方体展开图共11种,为方便大家记忆,总结如下:1.“141型”,中间一行4个作侧面,上下两个各作为上下底面,•共有6种基本图形。
2.“231型”,中间3个作侧面,共3种基本图形。
3.“222”型,两行只能有1个正方形相连。
4.“33”型,两行只能有1个正方形相连。
二、会判断哪两个面相对三、典型题目分析1、(2005·四川省)如图是一个正方体表面展开图,如果正方体相对的面上标注的值相等,那么x= ,y=2、下左图中,欲使相对两个面的数字互为相反数,则A=_____,B=____,C=___3、下右图中,哪两个数字相对?4、如图是立方体的表面展开图,要求折成立方体后,使得6在前,2在右,那么哪个面在上?5、有一个正方体,在它的各个面上分别写了①、②、③、④、⑤、⑥。
甲、乙、丙三位同学从三个不同的角度去观察此正方体,结果如下图,问这个正方体各个面的对面的是什么数?四、三视图⑥ ②④甲②③ ① 乙④ ③ ⑤ 丙562 1 34在生活中和数学中,对于不是很复杂的物体,如图所示通常从三个方向看,并画出图形,就可以大致搞清这个物体的外观了,这就是我们的课本是给出的:练习:1.如图,桌面上放着一个圆锥和一个长方体,其中俯视图形应该是( )2.下图是一个立体图形的三视图,请根据视图说出立体图形的名称( )从上面看从左面看从正面看主视图 左视图 俯视图A.圆柱B.圆台C.圆锥D.无法确定3.下列立体图形中有哪些图形的三视图都一样( ) A.圆柱 B.四面体 C.圆台 D.球4. 下面是由7块小正方体木块堆成的物体,从三个方向看到的图形如下,请同学们说出哪一个是主视图?哪一个是左视图?哪一个是俯视图?5:请同学们画出下列几何体的三视图6下图是几个小立方块所搭几何体的俯视图,小正方形中的数字表示在该位置的小立方块的个数,________图是这个几何体的主视图( )7图是由几个小立方体所搭几何体的俯视图,小正方形中的数字表示在该位置小正方体的个数。
正方体的平面展开图的判断问题
题目特点:选择题,给出正方体相邻的三个面,并且三个面上分别标有不同的图案,要求判断其平面展开图是哪一个。
解题方法:排除法。
先看选择项中标有图案的面是否相对,若相对,排除。
然后注意到带图案的三个面有一个公共点,在原图和展开图上标出这个公共点。
最后,将其中的两个折叠后复原(如前面的面和上边的面),看另一个面是否符合,找出正确
的答案。
注意:做题时,可将试卷旋转或颠倒一下判断,也可动手实际操作一下。
1.右面这个几何体的展开图形是()
2.如图几何体的展开图形最有可能是()
A、B、C、D、
3.如图所示的正方体,若将它展开,可以是下列图形中的()
A、B、C、D、
4.如图所示的立方体,将其展开得到的图形是()
A、B、C、D、
5.四个图形是如图的展开图的是()
A、B、C、D、
6.如左图所示的正方体沿某些棱展开后,能得到的图形是()
A、B、C、D、
A B C D
7.将如图所示表面带有图案的正方体沿某些棱展开后,得到的图形是()
A、B、C、D、
8.一个三面带有标记的正方体,如果把它展开,应是下列展开图形中的()
A、B、C、D、
9.下图右边四个图形中,哪个是左边立体图形的展开图?()
A、B、C、D、
10.如图,有一个正方体纸盒,在它的三个侧面分别画有三角形、正方形和圆,现用一把剪刀沿着它的棱剪开成一个平面图形,则展开图可以是()
A、B、C、D、
11.将如图正方体的相邻两面上各画分成九个全等的小正方形,并分别标上O、×两符号.若下列有一图形为此正方体的展开图,则此图为()
A、B、C、D、
1.下面简单几何体的左视图是( ).
2.如图所示,右面水杯的俯视图是( )
A.B.C.D.
正面
321213、如图(1)放置的一个机器零件,若从正面看是如图(2),则其左面看是( ) 4. 若右图是某几何体的三种不同方向的图,则这个几何体是( )
A.圆柱
B.正方体
C.球
D.圆锥
5. 图所示的物体,从左面看得到的图是( )
6、如图所示是由四个相同的小正方体组成的立体图形,它的俯视图为( )
7、如图2,这是一个正三棱柱,则从上面看到的图为
( )
8、如图是由七个相同的小正方体堆成的物体,从上面看这个物体的图是( )
9、如图:是由几个小立方块搭成的几何体的俯视图,小正方形中的数字表示该位置小立方块的个数。
请
搭出这个物体,并画出该几何体的主视图、左视图
10、由一些完全相同的小立方块搭成的几何体的三种视图,那么搭成这个几何体所用的小立方块的个数
( ) A 、6个 B 、7个 C 、8个 D 、9个
主视图 左视图 俯视图
11、如图1,是由几个小立方块所搭几何体的俯视图,小正方形中的数字表示在该位置的小立方块的个数,
这个几何体的主视图是 ( )
A .
B .
C .
D .
(A ) (B ) (C ) (D ) ( 2)
( 1) (第3题) 正面
左面 上面 6A . B . C . D .
图1
1
1
1
2
A B C D
12、下面右边的图形是由8个棱长为1个单位的小立方体组成的立体图形,这个立体图形的左视图是
( )
13、某工艺品由一个长方体和球组成(右图),则其俯视图是( )
A. B. C. D.
13、下面右边的图形是由8个棱长为1个单位的小立方体组成的立体图形,这个立体图形的左视图是
( )
14、某几何体的三视图如左图所示,则此几何体是( )
A.正三棱柱B.圆柱C.长方体D.圆锥
15、由若干个同样大小的正方体堆积成一个实物,不同侧面观察到如图8所示的投影图,则构成该实物的
小正方体个数为( )
A. 6
B. 7
C. 8
D. 9
某超市货架上摆放着“康师傅”红烧肉面,如图1是
它们的三视图,则货架上的“康师傅”红烧肉面至少有( )
A.8桶B.9桶
C.10桶D.11桶
16、下列四个几何体中,已知某个几何体的主视图、左视图、俯视图分别为长方形、长方形、圆,则该几
何体是()
A.球体B.长方体C.圆锥体D.圆柱体
17、下列几何体,正(主)视图是三角形的是( )
A. B.
主视图左视图俯视图
图1
正方体的平面展开图的判断问题答案
1.分析:由平面图形的折叠及正方体的展开图解题,注意带图案的三个面有一个公共顶点.
解:选项B、C带图案的三个面不相邻,没有一个公共顶点,不能折叠成原正方体的形式,排除;选项A 能折叠成原正方体的形式,而选项D折叠后带圆圈的面在上面时,带三角形的面在左边与原正方体中的位置不同,故选A.
点评:解题时勿忘记四棱柱的特征及正方体展开图的各种情形.注意做题时可亲自动手操作一下,增强空间想象能力.
2.C.3.C.4.D.5.A.6.B.7.C.8.D.9.B.10.C.
11.分析:此题主要根据O、×两符号的上下和左右位置判断,可用排除法.解:由已知图可得,O、×两符号的上下位置不同,故可排除A、B;又注意到O、×两符号之间的空行有3列,故选C.。