飞轮转动惯量公式与电机用飞轮例题
- 格式：pdf
- 大小：349.54 KB
- 文档页数：5
下载文档原格式
合集下载
转动惯量实例及解析
同方向性。
3. 力矩的累积效应
（1）空间累积：
力矩的功 W = ∫ M ⋅ d θ
动能定理 W
=
1 2
Jω
2 2
−
1 2
J
ω
2 1
∫ ∑ （2）时间累积 角动量定理：
r M
⋅ dt
=
Jωr 2
−
Jωr1
4. 角动量守恒定律
∑ ∑ 当
r M
=
0
时，有
r L
=
J iωr i
=
r C
说明：(1) 一个刚体
O点转动的角速度ω。
v0 L/2
L/2
O
L v0
∫ ∫ 解:碰前
3L / 2
dm
−L/2
⋅ v0
⋅x
=
3L / 2 −L/2
m 2L
v0 xdx
=
1 2
mv0L
其中 dm = m dx 2L
碰后 (J1 + J 2 )ω
v0
O x
J1
=
1 3
⋅
m 2L
⋅ 3L 2
⋅(3L )2 2
dx
J2
=
1⋅ m 3 2L
刚体定轴转动习题课
一、内容小结
1.基本概念:(1)角速度矢量 ω
(2)转动动能
Ek
=
1 2
Jω 2
∑ ∫ (3)转动惯量 J = ∆miri2 = dm⋅r2
r
×
r F
(5)角
动
量
r L
= rr × mvr = Jωr
2.
r 转动定律: M
= Jαr
r M
飞轮转动惯量计算公式详细介绍
飞轮转动惯量计算公式详细介绍 安装在机器回转轴上的具有较大转动惯量的轮状蓄能器。
当机器转速增高时，飞轮的动能增加，把能量贮蓄起来；当机器转速降低时，飞轮动能减少，把能量释放出来。
飞轮可以用来减少机械运转过程的速度波动。
具有适当转动惯量、起贮存和释放动能作用的转动构件，常见于机器、汽车、自行车等，具有较大转动惯量的轮状蓄能器。
飞轮的功能 ①将发动机作功行程的部分能量储存起来，以克服其他行程的阻力，使曲轴均匀旋转。
②通过安装在飞轮上的离合器，把发动机和汽车传动系统连接起来。
③装有与起动机接合的齿圈，便于发动机起动。
飞轮的功用 在曲轴的动力输出端，也就是连变速箱和连接做功设备的那边。
飞轮的主要作用是储存发动机做功冲程外的能量和惯性。
四冲程的发动机只有做功一个冲程吸气、压缩、排气的能量来自飞轮存储的能量。
平衡纠正一下不对，发动机的平衡主要靠去轴上的平衡块单缸机专门有平衡轴。
飞轮具有较大转动惯量。
由于发动机各个缸的做功是不连续的，所以发动机转速也是变化的。
当发动机转速增高时，飞轮的动能增加，把能量贮蓄起来;当发动机转速降低时，飞轮动能减少，把能量释放出来。
飞轮可以用来减少发动机运转过程的速度波动。
装在发动机曲轴后端，具有转动惯性，它的作用是将发动机能量储存起来，克服其他部件的阻力，使曲轴均匀旋转;通过安装在飞轮上的离合器，把发动机和汽车传动连接起来;与起动机接合，便于发动机起动。
并且是曲轴位置传感和车速传感的集成处。
在作功行程中发动机传输给曲轴的能量，除对外输出外，还有部分能量被飞轮吸收，从而使曲轴的转速不会升高很多。
在排气、进气和压缩三个行程中，飞轮将其储存的能量放出来补偿这三个行程所消耗的功，从而使曲轴转速不致降低太多。
除此之外，飞轮还有下列功用：飞轮是摩擦式离合器的主动件；在飞轮轮缘上镶嵌有供起动发动机用的飞轮齿圈；在飞轮上还刻有上止点记号，用来校准点火定时或喷油定时，以及调整气门间隙。
2转动惯量和飞轮转矩折算
n f（TL）
2.3.2 分类 • 恒转矩型机械特性（TL为常数）
•
• •
恒功率型机械特性（P为常数）
离心式通风机型机械特性 直线型机械特性
1) 恒转矩型机械特性（TL为常数）
(a) TL为反抗转矩（摩擦转矩）时， l 恒与运动方向相反，阻碍运动 l 符号总是正的 l 如：金属切削机床等（切削力）
2.4 系统稳定运行条件
2.4.1 基本要求 系统稳定运行，即电动机的机械特性与生产机械 的机械特性配合好。
2.4.2 稳定运行的含义
1) 系统匀速运转
2) 在干扰消除后，系统恢复到原运行速度
2.4.3 稳定运行的条件
n f（TM），
n f（TL）
n n０ na n’a
1) 必要条件
a
TM = TL ，方向相反，两特性曲线有
（加速， TM TL ）
2) 制动
TM TL
2.2.1 负载转矩折算（ TL 为静态转矩）
根据静态时功率守恒原则，则 1) 旋转运动
' ' P P T 出 L L L 传动效率 C P入 PM TL M
2.1.3 转矩方向的确定
1) TM与n方向一致 TL与n方向相反 2) TM与n方向相反 TL与n方向一致 TM取“+”号（拖动转矩TM） TL取“+”号（制动转矩TL） TM取“-”号（制动转矩TM） TL取“-”号（拖动转矩TL）
2.1.4 举例（如提升机）
1) 启动
TM TL Td 0
2.1 运动方程式
单轴机电传动系统如图所示：
+ω
+TM
生产机械
M
+TL
转动惯量和飞轮转矩折算
(2.2)
2 2 2 式中：J——转动惯量（ J m mD / 4 GD / 4g ）
GD2——飞轮惯量（飞轮转矩）
rad / s 2 nr / min
60
g = 9.81 m/s2
2.1.2 动态转矩Td
TM TL Td
或
TM TL Td
注：
当电动机转矩TM =负载转矩 TL时，动态转矩 Td = 0，系统处于静态或稳态，静态转矩TL也称 为稳态转矩。
2 GDL 2 jL
(当 j1 较大时) ( 取1.1~1.25)
2 式(2.4)改为： GDZ2 GDM
2) 直线运动
JZ JM J1 J L 2 2 2 m 2 j1 jL M
2 2 2 G GD GD N m / s 2 2 1 L GD M 2 2 365 2 j1 jL nM r / min 2
n n0 b点是稳定平衡点。 （∵ n > n ｂ
b b
，TM < TL ；
n < n
，TM > TL）
Ｏ
Ｔ
异步电动机拖动直流他励发电机工 作时的特性
作业： P:13 2.1 ～ 5 ， 2.7 ～ 11 （在题 2.8 中，划去
“以及折算……飞轮惯量GDZ2）
2.1.3 转矩方向的确定
1) TM与n方向一致 TL与n方向相反 2) TM与n方向相反 TL与n方向一致 TM取“+”号（拖动转矩TM） TL取“+”号（制动转矩TL） TM取“-”号（制动转矩TM） TL取“-”号（拖动转矩TL）
2.1.4 举例（如提升机）
1) 启动
TM TL Td 0
转动惯量和飞轮力矩的关系
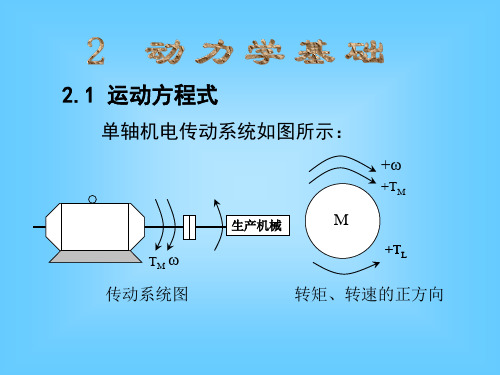
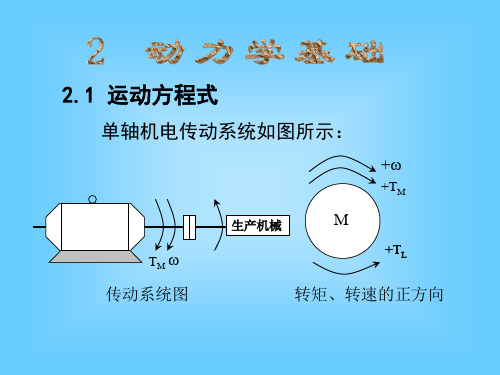
转动惯量和飞轮力矩的关系转动惯量和飞轮力矩的关系可不是一件简单的事，听起来就像是物理课上的一个老掉牙的话题，但其实这背后有很多有趣的故事哦。
想象一下，一个飞轮就像是个超级英雄，能在需要的时候给我们提供强大的动力。
它的转动惯量就像是它的身份牌，越重的身份牌，飞轮就越难以转动，但一旦它动起来，那可真是势不可挡。
你可能会想，飞轮和转动惯量之间到底有啥关系呢？哎，别急，慢慢来。
飞轮的力矩就像是小孩拉着风筝，风筝飞得越高，需要的力气就越大。
飞轮越重，转动惯量越大，要想让它转动起来，必须用更多的力矩。
这就好比你在运动的时候，想要举起一块大石头，光靠自己的力气可不够，得找个小伙伴帮忙。
这也解释了为什么在一些机械设备里，我们常常会看到飞轮的身影。
它们就是在帮助设备克服转动惯量，顺利运行。
大家都知道，惯性是物理中的“老大”，一旦飞轮转起来，简直就像是被施了魔法，转动的过程不再受到太多阻碍。
你会发现，飞轮在一些交通工具中尤其重要，像是汽车、火车、甚至是飞机。
想象一下，汽车在加速时，飞轮的力矩就像是给它打了一针强心剂，让它瞬间提速。
再比如，火车启动的时候，飞轮的转动惯量保证了它不会因为瞬间的加速而失控。
哇，这可真是个了不起的家伙，不是吗？而飞轮的设计就像是美食中的调味料，适当的添加才能让整体的性能达到最佳状态。
说到飞轮，咱们得提一下“平衡”这个概念。
飞轮在转动的时候，就像是一个调皮的小孩，随时可能摔倒，但如果设计得当，飞轮就能在转动中保持稳定。
想象一下，一个飞轮在快速旋转，它的重心就像是个魔术师，巧妙地保持平衡。
这个时候，转动惯量发挥了它的威力，让飞轮在各种环境中都能保持稳定，就算遇到风浪，也能轻松应对。
飞轮的力矩就像是一个坚实的后盾，让它在关键时刻展现出超强的能力。
再说说飞轮的应用吧，别小看它，这小东西在生活中可无处不在。
比如，洗衣机在甩干的时候，飞轮的力矩帮助衣物迅速脱水，几乎就像是给衣物上了个“干洗”的魔法。
健身器材中的飞轮，能够让你在锻炼时体验到更顺畅的感觉。
求主轴飞轮的转动惯量J
面积 10π /16 -20π /16 15π /16 -10π /16 10π /16 -10π /16
新疆大学专用
5π /16
作者： 潘存云教授
由能量指示图，得：
Amax＝10π /8＝3.93 KN-m
J
＝
Amax
/[δ
]ω
2 m
＝3.93×10/(0.05×252)
＝ 126 kgm2
Amax
选定飞轮的材料和比值H/B之后，可得飞轮截面尺寸。
盘形飞轮：
J
1 2
m
D 2
2
mD 8
2
D
选定圆盘直径D，可得飞轮的质量：
m＝Vρ
π D2B ρ =4
B
选定飞轮的材料之后，可得飞轮的宽度B。
为保证安全，飞轮的外圆线速度不能超过许用值：
新疆大学专用
铸铁飞轮： vmax≤ 36 铸钢飞轮： vmax≤ 50
新疆大学专用
作者： 潘存云教授
§7－3 飞轮主要尺寸的确定
轮形飞轮：由轮毂、轮辐和轮缘三部分组成。
主要尺寸：宽度B、轮缘厚度H、平均值径Dm
JA 轮幅
轮缘
轮毂
Dm
H
B
其轮毂和轮缘的转动惯量较小，可忽略不计。其转
动惯量为：
J
m
Dm 2
2
mDm2 4
新疆大学专用
作者： 潘存云教授
按照机器的结构和空间位置选定Dm之后，可得飞轮质量： m＝Vρ =π DmHB ρ ρ 为材料密度
驱动发电机的活塞式内燃机，主轴速度波动范围太大，势必影响输出电压的稳定性，故这类机械的 δ 应取小些；反之，如冲床、破碎机等机械，速度波动大也不影响其工作性能，故可取大些
初三物理飞轮转速问题20道
初三物理飞轮转速问题20道物理飞轮转速问题是物理学中比较重要的一个概念，也是初三物理课程的内容之一。
下面我将为你解答20道相关的问题，帮助你更好地理解飞轮转速。
1.什么是飞轮的转速？如何表示？飞轮的转速是指单位时间内飞轮旋转的圈数。
通常用r/min（每分钟转数）或rad/s（弧度/秒）来表示。
2.飞轮的转速与什么因素有关？飞轮的转速与外力、摩擦力、惯量和扭矩有关。
3.什么是飞轮的惯量？飞轮的惯量指的是飞轮旋转时对转轴的惯性作用。
飞轮的惯量越大，转动越困难。
4.飞轮的转速与摩擦力有什么关系？摩擦力越大，飞轮的转速越难以改变。
5.飞轮的转速与外力有什么关系？外力越大，飞轮的转速越容易改变。
6.飞轮的转速与扭矩有什么关系？扭矩越大，飞轮的转速越容易改变。
7.什么是飞轮的动能？飞轮的动能是指飞轮旋转时具有的能量。
8.飞轮的转速与动能有什么关系？转速越高，飞轮的动能越大。
9.如何计算飞轮的转速？飞轮的转速可以通过计算飞轮旋转的圈数和用时来求得。
例如，若飞轮旋转了10圈，用时为30秒，则转速为10圈/30秒=1/3圈/秒。
10.如何提高飞轮的转速？可以通过减小外力和摩擦力，增大扭矩来提高飞轮的转速。
11.为什么飞轮的转速比较难改变？飞轮具有惯性，惯性作用使得飞轮的转速比较难以改变。
12.在飞轮旋转时，如何改变其转速？可以通过施加外力或改变飞轮的摩擦力来改变其转速。
13.什么是角加速度？角加速度是指飞轮旋转时转速的变化率。
通常用符号α表示。
14.角加速度与飞轮的转速有什么关系？角加速度越大，转速变化越快。
15.如何计算飞轮的角加速度？飞轮的角加速度可以通过计算转速的变化值与时间的比值来求得。
例如，若30秒内转速增加了2圈，则角加速度为2圈/30秒=1/15圈/秒²。
16.什么是动力矩？动力矩是指外力或摩擦力对飞轮产生的转动效果。
通常用符号τ表示。
17.动力矩与飞轮的转速有什么关系？动力矩越大，转速变化越快。
转矩、转动惯量和飞轮转矩的折算
转矩、转动惯量和飞轮转矩的折算
例题
• 动力学
位移与角度 速度 加速度 质量、转动惯量、飞轮转矩 牛顿定律 功、功率、动能
• • • • •
折算的原则 转矩的折算 作用力的折算 转动惯量和飞轮转矩的折算 直线运动质量的折算
例1 、
• 图示的电机拖动系统中，已知飞轮矩GDm2=14.7N· m2， GD12=18. 8 N· m 2，GDL2=120 N· m 2，拖动效率η1=0.91， η2=0.93，负载转矩TL=85 N· m，转速n=2450r/min， n1=810r/min，nL=150r/min，忽略电动机空载转矩，求： • 折算到电动机轴上的系统总惯量J； • 折算到电动机轴上的负载转矩 。
2 1 GDd dn 1 + ( 2 2 2) 375 j1 j 2 j3 dt 1 2 3
800 2 2 .7 9 (3.5+ 2 + 2 + ) 2 2 2 2 2 3 375 2 0.9 2 1.5 0.9 2 1.5 2 0.9 800 4.769=10.17 N .m 2 = 375
2n f
150 2 3.1416 241.7 103 3.796KW 切削功率 P T f T 60 60
( 2 )电动机输出功率 P2
P
1 2 3
2 a
3.796 5.207KW 0.9 0.9 0.9
2 GDb2 GDc2 GDd ( 3 )系统总飞轮矩 GD GD 2 2 2 2 2 2 j1 j1 j 2 j1 j2 j3 2
2
m , GDc2 =2 .7 N· m , GDd2 =9 N· m ,各级传动效率1 = 2 =3 =90% , 动机轴), GDb2 = 2 N·
例题
• 动力学
位移与角度 速度 加速度 质量、转动惯量、飞轮转矩 牛顿定律 功、功率、动能
• • • • •
折算的原则 转矩的折算 作用力的折算 转动惯量和飞轮转矩的折算 直线运动质量的折算
例1 、
• 图示的电机拖动系统中，已知飞轮矩GDm2=14.7N· m2， GD12=18. 8 N· m 2，GDL2=120 N· m 2，拖动效率η1=0.91， η2=0.93，负载转矩TL=85 N· m，转速n=2450r/min， n1=810r/min，nL=150r/min，忽略电动机空载转矩，求： • 折算到电动机轴上的系统总惯量J； • 折算到电动机轴上的负载转矩 。
2 1 GDd dn 1 + ( 2 2 2) 375 j1 j 2 j3 dt 1 2 3
800 2 2 .7 9 (3.5+ 2 + 2 + ) 2 2 2 2 2 3 375 2 0.9 2 1.5 0.9 2 1.5 2 0.9 800 4.769=10.17 N .m 2 = 375
2n f
150 2 3.1416 241.7 103 3.796KW 切削功率 P T f T 60 60
( 2 )电动机输出功率 P2
P
1 2 3
2 a
3.796 5.207KW 0.9 0.9 0.9
2 GDb2 GDc2 GDd ( 3 )系统总飞轮矩 GD GD 2 2 2 2 2 2 j1 j1 j 2 j1 j2 j3 2
2
m , GDc2 =2 .7 N· m , GDd2 =9 N· m ,各级传动效率1 = 2 =3 =90% , 动机轴), GDb2 = 2 N·
第三章 电动机和飞轮的计算
第三章 电动机和飞轮的计算第1节 总论曲柄压力机的工作特点是一短时间的高峰负荷，单独用电动机不可能满足扭矩的急剧变化的需要，采用飞轮后则能够把电动机不断供给它的能量株存起来，压力机在完成工序时，飞轮通过降低转速输出部分贮存的能量，在空行程时，再由电动机加速飞轮，以恢复动能的贮备。
在有飞轮的压力机中，由于工作行程时的高峰负荷主要由飞轮承担，所以电动机的功率比不用飞轮时可以减小到十二分之一。
例如：有飞轮的压力机其电动机为50千瓦时，没有飞轮的压力机需要600千瓦的电动机才足以供给压力机高峰扭矩的需要。
由此可见，采用飞轮可以颇大地减小电动机的额定功率，提高电动机的利用率，降低成本。
贮存在飞轮中的总能量为：E=21J ω²千克—米 （3-1a ）式中：J —飞轮及其连接部件的转动惯量（千克—米—秒²） ω—飞轮自由旋转时的角速度(弧度/秒) 飞轮在工作行程中所供给的功为:E=21J(ω1²-ω2²)千克-米 （3-1b ）式中: ω1—飞轮的初始角速度（弧度/秒）ω2—飞轮工作行程结束时的飞轮角速度（弧度/秒）从（3—1b ）式中看出：当飞轮速度降低10％时，飞轮供给的能量为其总能量的19％，降低20％时为36％，80％为51％。
由此可见，飞轮速度降低10％比降低20％其输出能量少将近一倍。
换句话说，如果输出功相等，前者的转动惯量应该比后者大将近一倍。
从设计的角度看，应该尽量减轻飞轮的重量和尺寸。
飞轮的惯量过大，不仅增加了制造成本，而且在发生事故时加剧了灾难性。
所以，在设计计算时，应该使飞轮的速度降尽可能大些。
但是，当飞轮的速度降低时，电动机的转速也跟着降低，电机的工作电流将成比例地增加，使电机的工作情况恶化。
图（3—1）表示电机的工作电流I 与转矩M 随其转差率S 的变化情况。
从图中看出，当S 增加时M 和I 开始于S 成正比例增加促使飞轮迅速恢复原有转速，这是我们所希望的。
初三物理飞轮的练习题
初三物理飞轮的练习题题目一：飞轮的动能一个半径为8cm，质量为0.5kg的飞轮以200 rad/s的角速度旋转。
求飞轮的动能。
解析：飞轮的动能可以通过以下公式计算：动能= 1/2 * I * ω²其中，I表示飞轮的转动惯量，ω表示角速度。
由于飞轮是围绕自身转动，因此可以将它近似看作是一个实心圆盘，其转动惯量的计算公式为：I = 1/2 * m * r²其中，m表示飞轮的质量，r表示飞轮的半径。
将已知数据代入计算公式，可得：I = 1/2 * 0.5kg * (0.08m)² = 0.0024kg·m²将转动惯量和角速度代入动能计算公式，可得：动能 = 1/2 * 0.0024kg·m² * (200rad/s)² = 0.048J因此，飞轮的动能为0.048焦耳。
题目二：飞轮的角加速度一个直径为20cm，质量为1kg的飞轮，静止时被水平力拉绳加速拉动，使其在2s内转速达到每分钟1800转，求飞轮的角加速度。
解析：首先，我们需要将每分钟1800转的转速转换为弧度/秒的角速度。
1分钟 = 60秒1800转= 1800 * 2π弧度= 3600π弧度所以，飞轮的角速度为：ω = 3600π rad/60s = 60π rad/s我们使用以下公式计算飞轮的角加速度：α = (ω - ω₀) / t其中，α表示角加速度，ω₀表示初始角速度，ω表示最终角速度，t 表示时间。
因为飞轮开始时静止，所以初始角速度ω₀为0。
将已知数据代入计算公式，可得：α = (60π rad/s - 0) / 2s = 30π rad/s²因此，飞轮的角加速度为30π rad/s²。
题目三：飞轮的转动惯量一个飞轮的半径为10cm，质量为0.8kg。
通过实验得知，飞轮在固定轴上转动时，它的振动周期为2s。
求飞轮的转动惯量。
解析：根据实验得知的振动周期可求得飞轮的角频率。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
飞轮的转动惯量确定后，就可以确定其各部分的尺寸了。
需要注意的是，
在上述讨论飞轮转动惯量的求法时，假定飞轮安装在机械的等效构件上。
实际
设计时，若希望将飞轮安装在其它构件上，则在确定其各部分尺寸时需要先将
计算所得的飞轮转动惯量折算到其安装的构件上。
飞轮按构造大体可分为轮形
和盘形两种。
●轮形飞轮
图中，这种飞轮由轮毂、轮辐和轮缘三部分组成。
由于与轮缘相比，其它
两部分的转动惯量很小，因此，一般可略去不计。
这样简化后，实际的飞轮转
动惯量稍大于要求的转动惯量。
若设飞轮外径为D1，轮缘内径为D2，轮缘质量
为m，则轮缘的转动惯量为
(10.28)
当轮缘厚度H 不大时，可近似认为飞轮质量集中于其平均直径D 的圆周上，
于是得
(10.29)
式中， m D2称为飞轮矩 ，其单位为kg·m2。
知道了飞轮的转动惯量 ，就可以
求得其飞轮矩。
当根据飞轮在机械中的安装空间，选择了轮缘的平均直径D后，
即可用上式计算出飞轮的质量 m。
若设飞轮宽度为B （m），轮缘厚度为H（m），平均直径为D（m），材料密度
为ρ（kg·m3)，则
(10.30)
在选定了D并由式(10.28)计算出m后，便可根据飞轮的材料和选定的比值H/B
由式（10.30）求出飞轮的剖面尺寸H和B，对于较小的飞轮，通常取H/B≈2，
对于较大的飞轮，通常取H/B≈1.5。
由式(10.29)可知，当飞轮转动惯量一定时，选择的飞轮直径愈大，则质量
愈小。
但直径太大，会增加制造和运输困难，占据空间大。
同时轮缘的圆周速度
增加，会使飞轮有受过大离心力作用而破裂的危险。
因此，在确定飞轮尺寸时应
核验飞轮的最大圆周速度，使其小于安全极限值。
●盘形飞轮
当飞轮的转动惯量不大时，可采用形状简单的盘形飞轮，如图所示。
设m ，D和B分别为其质量、外径及宽度，则整个飞轮的转动惯量为
(10.31)
当根据安装空间选定飞轮直径D后，即可由该式计算出飞轮质量m 。
又因
，故根据所选飞轮材料，即可求出飞轮的宽度B为
(10.32)
返回
【典型例题】
旋转物体的转动惯量J与飞轮矩GD2都是表是质量元素及其相对于转轴的关系，两者概念相似，但表达的内容不同，在平时的计算和交流中常常容易混淆。
下面通过公式就能很清楚的看出两者的区别。
转动惯量=M×ρ2，其单位是kgm2
飞轮力矩=G×D2，其单位是Nm2
其中，G代表旋转物体的质量；
ρ表示基于转轴的旋转半径；
D表示基于转轴的旋转，直径D=2ρ。
因此GD2=4g×J
在电机起动计算中，转动惯量直接影响起动时间的计算，一旦出错，会使计算结果相去甚远，甚至是作出相反的结论。
对此，我们在工程计算时一定要保持高度的敏感性。
例5 在一台用电动机
作原动机的剪床机械系
统中，电动机的转速为
n m=1500 r/min 。
已知折
算得电机轴上的等效阻
力矩 M r 的曲线如图
（ a ）所示，电动机的
驱动力矩为常数；机械系
统本身各构件的转动惯
量均忽略不计。
当要求该
系统的速度不均匀系数
为 δ≤ 0.05 时，求安装在
电机轴上的飞轮所需的
转动惯量 J F 。
解 取电动机轴为等效构件
（1）求等效驱动力矩 M
d
图中只给出了等效力矩M
r
的变化曲线，并知道电动机的驱动力矩为常数，
但不知其具体数值。
根据一个周期内等效驱动力矩 M
d
所做功等于等效阻力矩 M d 所消耗功的原则可得
求最大盈亏功[W]
在图中画出等效驱动力矩 M d =462.5 N ∙ m 的直线，它与 M r 曲线之间所夹的各单元面积所对应的盈功或亏功分别为
J
=-1256.3 J
+(4625-200)×π=844 J
根据上述结果绘出能量指示图（b ），可见，最大盈亏功即为 f
2 或 f
1
+f
2。
即
[W]=1256.3 J
（2)求飞轮的转动惯量
（3)将[W] 代入飞轮转动惯量计算式，可得
kg·m2
由此例可知，不论已知M
d 的规律或 M
r
的规律，总可以运用在一个周期内
等效驱动力矩所做的功应等于等效阻力矩所消耗的功（输入功等于输出功）的原则，求出未知的一个常数力矩，然后 求出最大盈亏功[W] 。