画图法解应用题
- 格式:doc
- 大小:29.50 KB
- 文档页数:4


【例1】朗读小组的同学排成一排表演诗朗诵,从左边数起,玲玲是第8个,从右边数起,玲玲是第7个,有多少同学参加表演?随堂练习11、排排队,来报数,正着报数我报6,倒着报数我报9,请你算一算,一共有多少个小朋友在报数?【例2】有16名同学排成一队,小小排在小亚的前面,从前往后数,小亚排在第9个,从后往前数,小小排在第10个,他们之间隔着几个人?随堂练习216个小朋友排成一队去看电影,胖胖在小明的后面,从前往后数,小明在第5个,从后往前数,胖胖排在第8个,小明和胖胖之间隔了几个人?【例3】小明有10支铅笔,小红有4支铅笔,要使两人的铅笔同样多,小明要给小红几只铅笔?随堂练习3沈老师有12本练习本,李老师有18本练习本,要使两人的练习本同样多,李老师要给沈老师多少本练习本?【例4】一排20个座位,其中有些座位已经有人,小明无论坐在哪一个座位上,旁边都有一个人与他相邻,那么原来至少有多少人已经就座?随堂练习4一排10个座位,其中有些座位已经有人,小刚无论坐在哪一个座位上,旁边都有一个人与他相邻,那么原来至少有多少人已经就座?【例5】二(1)班有学生25人,比二(2)班少4人,二(2)班比二(3)班多3人,三个班一共有学生多少人?随堂练习5苹果有30筐,香蕉比苹果多12筐,比芒果少12筐,三种水果一共有多少筐?练习题:1、二年一班22个小朋友排成一队去操场做操,从最前面数到丁丁是第9个,君君排在丁丁的后面,从队伍的最后往前数,君君排在第几个?2、第一队的同学排成一排,排在东东前面的有6个小朋友,排在东东后面的有4个小朋友,第一队一共有几个小朋友?3、小朋友们排成一队参观博物馆,从排头数起牛牛是第10个,从排尾数起妞妞是第18个,排在牛牛前面的就是妞妞,一共有多少个小朋友去参观博物馆?4、在20米的校园小道一边种杨柳树,每隔4米种一棵,两端都种,想一想,一共要种几棵树?5、小明给小红4支铅笔后,两人的支数相同,问:小明比小红多几支铅笔?6、哥哥有4支铅笔,弟弟给哥哥3支铅笔后,两人的支数相同,弟弟原来有几支铅笔?7、一根16米长的木条,把它锯成4段,要锯几次?8、晓丁从一楼走到四楼用了9分钟,照这样计算,从一楼走到七楼需要几分钟?9、妈妈到水果店买苹果,她带的钱若买3千克多2元,若买4千克少3元,问:妈妈带了多少钱去买苹果?10、体育小组有20个学生,排成两排队伍做早操,每两个学生之间相隔1米,每排队伍有多长?11、李老师把同学们的画排成一行,无论是从左边数起,还是从右边数起,方方的画都排第8张。

线段图法例:两个小同学折纸鹤,小红折的数量比小丽的3倍还多5个,她俩一共折了53个,问两个人分别折了多少个?根据题意作图:解析:看这个线段图,很容易发现53-5,得出的结果再平均分成4份,其中的1份就是小丽折的纸鹤个数.列式计算:小丽折的个数:(53-5)÷4=12(个),小红折的个数:12 ×3+5=41(个).平面图法例:有两个自然数A和B,如果把A增加12,B不变,积就增加72;如果A不变,B增加12,积就增加120,求原来两数的积.解析:这道题可以画长方形图来具象化,长表示A,宽表示B,那么两数的积就是长方形的面积.A、B原来两数用长方形图a表示,当A增加12即长增加12,宽不变,即B不变,如图b;当B增加12即宽增加12,长不变,也就是A不变,如图c.所以:长方形的宽也就是B=72÷12=6,长方形的长也就是A=120÷12=10,那么,A、B的积为6×10=60.立体图法例:把一个正方体切成两个长方体,表面积就增加了8平方米.原来正方体的表面积是多少平方米?根据题意作图:解析:由图可知,增加的8平方米,就是正方体的2个面,每个面的面积是8÷2=4(平方米),则正方体的表面积是:4×6=24(平方米).列表图法例:有一个5分币,4个2分币,8个1分币.要拿9分钱,有几种拿法?根据题意作图:由列表图,可以清楚看到共有7种拿法.树状图法例:小明是个小马虎,晚上睡觉时将两双不同的袜子放在床头,早上起床没看清就随便穿了两只.小明正好穿的是同一双袜子的可能性是多少?解析:假设2双袜子为A袜、B袜,那么4只袜子分别是A1、A2、B1、B2,根据题意作图:由树状图可知,2双袜子任意搭配有12种情况,其中同一双的情况有4种,所以小明穿同一双袜子的的可能性是4/12,也就是1/3.。



画图法解应用题一、夯实基础在解答一些应用题时,用作图法可以把题目的数量关系揭示出来,使题意形象具体,一目了然,从而有助于快速找到解题的途径。
作图法解题可以画线段图,也可以画示意图,对解答条件隐蔽,复杂疑难应用题,能起到化难为易的作用。
例如在解答和差、和倍和差倍三类问题时,都可以用画图法表示。
简图如下:(1)和差问题(2)和倍问题(3)差倍问题二、典型例题例1.哥弟俩共有邮票70张,如果哥哥给弟弟4张邮票,这时哥哥还比弟弟多2张。
哥哥和弟弟原来各有邮票多少张?分析:由已知条件“哥哥给弟弟4 张后,还比弟弟多2 张”画图如下,可知哥哥的邮票比弟弟多4×2+2=10 (张)。
解:弟弟有邮票:(70-10)÷2=30 张,哥哥有邮票:30+10=40 张。
答:弟弟有邮票30张,哥哥有邮票40张。
例2.果园里有桃树、梨树、苹果树共146棵。
桃树比梨树少7棵,苹果树比桃树多4棵,三种树各有多少棵?分析:先用线段图表示出三种树棵数之间的关系:从图上可以看出,梨树的棵数比桃树多7棵,苹果树的棵数比桃树多4棵,假设移动多的棵数,则两种果树共减少了7+4=11(棵),相应的总棵数就减少11棵:146-11=135(棵),而135棵对应的就是桃树棵数的3倍。
解:桃树:(146-7-4)÷3=45(棵),梨树:45+7=52(棵),苹果树:45+4=49(棵)。
答:桃树有45棵,梨树有52棵,苹果树有49棵。
例3.某公司三个厂区共有员工1900人,甲厂区的人数是乙厂区的2倍,乙厂区比丙厂区少300人,三个厂区各有多少人?分析:先用线段图表示出三厂区人数之间的关系:从图上可以看出,假设丙厂人数减少300人,总人数也减少300人,为1900-300=1600(人),此时总人数恰好是乙厂的4倍。
解:乙厂:(1900-300)÷4=400(人),甲厂:400×2=800(人),丙厂:400+300=700(人)。

画图法解应用题苏联教育家苏霍姆林斯基曾经说过:“如果哪个学生学会了画应用题,我就可以有把握地说,他一定能学会解应用题。
”可见,画图对于小学数学解决问题的重要性。
在解答一些应用题时,用作图法可以把题目的数量关系揭示出来,以其形象、直观的特点,使题意一目了然,对解答条件隐蔽,复杂疑难应用题,能起到化难为易,化繁为简的作用,从而有助于快速找到解题的途径,有效地提高学生的自我学习能力和创新能力,使学生学会学习。
作图法解应用题中,常见的数学图有以下几种:一、线段图线段图是由几条线段组合在一起,用来表示应用题中的数量关系,帮助人们分析题意,解答问题的一种平面图形。
线段图在小学数学应用题学习中它可以帮助学生轻松地解答复杂关系的应用题,强化数量关系的表述训练,能根据数量关系有序地进行解题演练。
举例:欢欢和喵喵共有25个本子,如果欢欢用去了3个本子,喵喵买回2个本子,那么她们的本子就一样多了,你知道她们原来各有本子多少个吗?列式计算:喵喵 (25-3-2)÷2=10(本) 欢欢 25-10=15(本)二、树形图在解答应用题时,我们常常采用枚举法把所有符合题目条件的对象一一列举出来。
我们采用画树形图的方法,借助树的分叉特征构造出的树形图可以对数学问题中有可能出现的多种可能逐一例举出来,不仅形象直观,而且有条理又不易重复或遗漏,使人一目了然,有助于作出正确的判断。
举例:一个口袋中装有红、白、绿三只小球,另一只口袋中装有红、白两只小球。
现从两只口袋中各取一只小球,求两只小球颜色一样的概率是多少?从图中可以看出,两只小球颜色搭配的可能性共6种,而两只小球颜色一样的可能性只有(红-红),(白-白)共2种,所以两只小球颜色一样的概率为三分之一。
三、集合图在数学中,经常用平面上封闭曲线的内部代表集合,以及用以表示集合之间的关系,这样的图形称之为“集合图”。
举例:参加跳绳的有6人,参加踢毽子的有7人,两项都参加的有3人,这个组共有几人?6+7-3=10(人)四、情景图把复杂的数学问题用简单的图画表示,把情景再现出来,让人有身临其境的感觉,便于学生理解和分析应用题。


线段图法例:两个小同学折纸鹤;小红折的数量比小丽的3倍还多5个;她俩一共折了53个;问两个人分别折了多少个?根据题意作图:解析:看这个线段图;很容易发现53-5;得出的结果再平均分成4份;其中的1份就是小丽折的纸鹤个数。
列式计算:小丽折的个数:(53-5)÷4=12(个);小红折的个数:12 ×3+5=41(个)。
平面图法例:有两个自然数A和B;如果把A增加12;B不变;积就增加72;如果A不变;B增加12;积就增加120;求原来两数的积。
解析:这道题可以画长方形图来具象化;长表示A;宽表示B;那么两数的积就是长方形的面积。
A、B原来两数用长方形图a表示;当A增加12即长增加12;宽不变;即B不变;如图b;当B增加12即宽增加12;长不变;也就是A不变;如图c。
所以:长方形的宽也就是B=72÷12=6;长方形的长也就是A=120÷12=10;那么;A、B的积为6×10=60。
立体图法例:把一个正方体切成两个长方体;表面积就增加了8平方米。
原来正方体的表面积是多少平方米?根据题意作图:解析:由图可知;增加的8平方米;就是正方体的2个面;每个面的面积是8÷2=4(平方米);则正方体的表面积是:4×6=24(平方米)。
列表图法例:有一个5分币;4个2分币;8个1分币。
要拿9分钱;有几种拿法?根据题意作图:由列表图;可以清楚看到共有7种拿法。
树状图法例:小明是个小马虎;晚上睡觉时将两双不同的袜子放在床头;早上起床没看清就随便穿了两只。
小明正好穿的是同一双袜子的可能性是多少?解析:假设2双袜子为A袜、B袜;那么4只袜子分别是A1、A2、B1、B2;根据题意作图:由树状图可知;2双袜子任意搭配有12种情况;其中同一双的情况有4种;所以小明穿同一双袜子的的可能性是4/12;也就是1/3。
第九站画图法解应用题月日姓名【知识要点】1.如果有倍数关系,先画倍数关系,然后再根据题意变化。
2.如果有等量关系,先画等量关系,然后再根据题意变化。
3.如果倍数关系和等量关系都有,则先画倍数关系,再画等量关系。
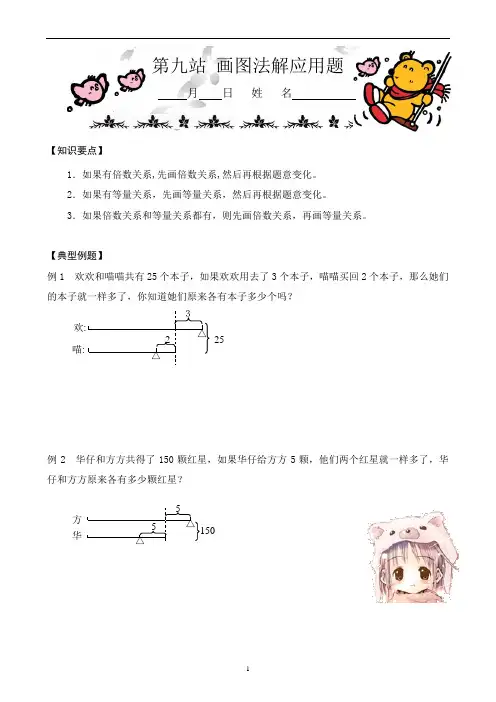
【典型例题】例1 欢欢和喵喵共有25个本子,如果欢欢用去了3个本子,喵喵买回2个本子,那么她们的本子就一样多了,你知道她们原来各有本子多少个吗?例2 华仔和方方共得了150颗红星,如果华仔给方方5颗,他们两个红星就一样多了,华仔和方方原来各有多少颗红星?2325欢:喵:△△5150△5华方△例3 在没有余数的情况下,被除数和除数之和为160,商是7,被除数和除数各是几?例4 利利有40个苹果,猪头有60个苹果,问利利给猪头多少个苹果,才能使猪头的苹果数是利利的4倍?变化前:利利:猪头: 4060△ △和: 变化后: 利利: 猪头:△和:△160??△ △被: 除:随堂小测姓 名 成 绩看线段图列式计算。
1. 2.列式: 列式:3. 4.列式: 列式:△ 257?△△76△? 31 318? △△17? △△ 30课后作业姓 名 成 绩 家长签名看线段图列式计算。
1. 2.列式: 列式:3. 4.列式: 列式:苹果: 桃子: ? 多6个 12个 苹果: 桃子:?个多8个 ?个 苹果: 桃子: 4个 共?个苹果: 桃子: ?个 ?个 共16个。

画图法解应用题例1:朗读小组的同学排成一排表演诗朗诵,从左往右数起,玲玲是第8个,从右边数起,玲玲是第7个,有多少个同学参加表演?练习:排排队,来报数,正着报数我报6,倒着报数我报9,请你算一算,一共有多少个小朋友在报数?例2:16名同学排成一队,小小排在小亚的前面,从前往后数,小亚排在第9个,从后往前数,小小排在第10个,他们之间隔着几个人?练习:16个小朋友排成一队去看电影,胖胖在小明的后面,从前往后数,小明排在第5个,从后往前数,胖胖排在第8个,小明和胖胖之间隔了几个人?例3:小明有10支铅笔,小红有4支铅笔,要使两人的铅笔同样多,小明要给小红几支铅笔?练习:王老师有12本练习本,李老师有18本练习本,要使两人的练习本同样多,李老师要给王老师多少本练习册?例4:一排20个座位,其中有些座位已经有人,小明无论坐在哪一个座位上,旁边都有一个人与他相邻,那么原来至少有多少人已经就座?练习:一排10个座位,其中有些座位已经有人,小刚无论坐在哪一个座位上,旁边都有一个人与他相邻,那么原来至少有多少人已经就座?例5:一条小街上,顺次安装有10盏路灯,为了节约用电又不影响路面照明,要关闭除首末两盏灯以外的8盏灯中的4盏灯,但被关的灯不能相邻,一共有几种不同的关法?练习:把4个一样的球放到两个相同的盒子里,有多少种不同的方法?例5:小明比小英小5岁,小方比小明大2岁.那么小英和小方差几岁?例6:小初、小美、小英三个人分糖块.小美比小英多3块,小初比小美多2块.已知糖块总数是50块,那么每人各分到多少块?例7:小健到商店去买练习本,他的钱若买4本还剩2分;若买5本,就差1角.问小健有多少钱?例8:妈妈的年龄是小铃的3倍,两个人年龄加起来是40岁.问小铃和妈妈各多少岁?例9:父亲今年40岁,小哲10岁.问几年以后父亲年龄是小哲年龄的2倍?练习题1、二年一班22个小朋友排成一队去操场做操,从最前面数到丁丁是第9个,君君排在丁丁的后面,从队伍的最后往前数,君君排在第几个?2、第一队的同学排成一排,排在东东前面的有6个小朋友,排在东东后面的有4个小朋友,第一队一共有几个小朋友?3、小朋友们排成一队参观博物馆,从排头数起牛牛是第10个,从排尾数起妞妞是第18个,排在牛牛前面的就是妞妞,一共有多少个小朋友去参观博物馆?4、在20米的校园小道一边种杨柳树,每隔4米种一棵,两端都种,想一想,一共要种几棵树?5、小明给小红4支铅笔后,两人的支数相同,问:小明比小红多几支铅笔?6、姐姐有4支铅笔,妹妹给姐姐3支铅笔后,两人的支数相同,妹妹原来有几支铅笔?7、一根16米长的木条,把它锯成4段,需要锯几次?8、小丁从一楼走到四楼用了9分钟,照这样的速度,从一楼走到七楼要用几分钟?9、妈妈到水果店买苹果,她带的钱若买3千克多2元,若买4千克少3元,问妈妈带了多少元钱去买苹果?10体育小组有20个学生,排成两排队伍做早操,每个学生之间相隔1米,每排队伍有多长?11、王强和李明都想买一本《趣味数学》,但王强的钱少2角5分,李明的钱少3角1分.如果两个人的钱合在一起就刚够买这本书.问一本《趣味数学》多少钱?王强和李明各有多少钱?12、大、小二数之和为10,之差为2,求大、小二数各多少?13、小军、小方和小雄共有12本小人书,小军比小方多2本,小方比小雄多2本,问他们三人各几本?14、今年弟弟8岁,哥哥14岁.问当两人的年龄和是30岁时,两人各几岁?15、两个桶里共盛水30斤.如果把第一个桶里的水倒3斤给第二个桶里,两个桶里的水就一样多了.问每个桶里各有多少斤水?16、玻璃瓶里装着一些水,把水加到原来的2倍时,称得重为5千克;把水加到原来的4倍时,再称一称重为9千克,问原来水有多少千克?17、一筐鲜鱼,连筐共重56千克.先卖出鲜鱼的一半,再卖出剩下的一半,这时连筐还重17千克.原来这筐鲜鱼重多少千克?18、小秋用一根绳子测量一口枯井的深.他把绳子放入井里,当绳子到达井底后,井外还留有15米;小秋又把这根绳子对折后再放入井里,井外还留有1米.请问,这口枯井有多少米深?。
例1、小红看一本故事书,第一天看的比全书的51少10页,还剩202页,这本故事书共多少页?练习:1、五年级有女生100人,男生人数比全年级总人数的41多5人。
全年级共多少人?例2、小红看一本故事书,第一天看的比全书的51少10页,第二天看的比全书的61多12页,最后还剩150页。
这本故事书共有多少页?练习:1、水果店有苹果、香蕉、梨三种水果,其中苹果比总数的31多10千克,梨比总数的41少2千克,香蕉重42千克,苹果和梨各多少千克?例3、有苹果和梨若干个,梨的个数是全体的53少17个,苹果的个数是全体的74少31个。
梨和苹果共多少个?第六讲 图解法解分数应用题C A B 水 练习:1、甲、乙两车分别从A 、B 两地同时出发,相向而行,相遇时甲行了全程的83少20千米,乙行了全程的43多5千米。
A 、B 两地相距多少千米?例4、一根木头,锯掉51后,又接上6米,这时是原长的1011。
求原长。
练习:1、一根木头,锯掉51后,又接上6米,这时比原长的1011多3米。
求原长。
综合练习:1、小明三天看完一本故事书,第一天看了全书的41还少4页,第二天看了全书的31还多14页,第三天看了90页,这本故事书一共有多少书?2、一整桶汽油,用去107后,又倒入10千克汽油。
这时汽油正好是原来的一半。
原来有多少千克汽油?3、操场上有一些同学,走了51后,又来了20人,这时比原来少151,求原来有多少人?4、A 、B 、C 三根木棒插在水池中,(如图)三根棒长度和是360厘米,A 棒有43露出水面外,B 棒 有74露出水面外.C 棒有52露出水面外.水池有 多深?。
分数的应用题六种解法分数是数学中常见的表示比例和部分的方式,它在生活中的应用也非常广泛。
今天,我将为大家介绍六种解决分数应用题的方法。
一、画图法画图法是一种直观的解题方法。
以某个具体的例子来说明。
假设小明有2/3的巧克力,小红有1/4的巧克力,他们想将巧克力平均分配。
我们可以画两个巧克力盒,并按比例将巧克力分配给小明和小红。
这样,他们就可以直观地理解分配的过程。
二、找最小公倍数解决一些关于分数的应用题时,我们需要找到最小公倍数。
例如,小明每天按照1/5的速度走路,小红按照1/3的速度走路,他们同时从同一个地方出发,问多少天后他们会在同一个地方相遇。
我们可以找到1/5和1/3的最小公倍数,即15。
因此,他们将在15天后相遇。
三、转化为整数运算有些分数应用题可以转化为整数运算来解决。
例如,小明用1/2小时完成作业,小红用1/3小时完成同样的作业,问他们两人一起完成这个作业需要多长时间。
我们可以将1/2和1/3转化为分母的最小公倍数,即6。
因此,他们一起完成这个作业需要1/6小时。
四、比较大小在比较大小的应用题中,我们需要将两个或多个分数进行比较。
例如,小明用2/5的时间做数学题,用1/4的时间做英语题,问他用了更多的时间做数学题还是英语题。
我们可以将2/5和1/4的分母取相同的最小公倍数,即20。
然后比较分子的大小,即2和5,得出结论小明用了更多的时间做数学题。
五、分数的加减运算在分数的加减运算中,我们需要将分母相同的分数进行运算。
例如,小明走了3/5的路程,小红走了2/5的路程,问他们总共走了多少路程。
我们可以将3/5和2/5的分母取相同的最小公倍数,即5。
然后将分子相加,得到答案5/5,即1。
因此,他们总共走了1个路程。
六、分数的乘除运算在分数的乘除运算中,我们需要将分子进行运算,再将分母进行运算。
例如,小明用2/3小时做完一个作业,小红用3/4小时做同样的作业,问小红完成这个作业需要多长时间。
线段图法例:两个小同学折纸鹤,小红折的数量比小丽的3倍还多5个,她俩一共折了53个,问两个人分别折了多少个?根据题意作图:解析:看这个线段图,很容易发现53-5,得出的结果再平均分成4份,其中的1份就是小丽折的纸鹤个数。
列式计算:小丽折的个数:(53-5)÷4=12(个),小红折的个数:12 ×3+5=41(个)。
平面图法例:有两个自然数A和B,如果把A增加12,B不变,积就增加72;如果A不变,B增加12,积就增加120,求原来两数的积。
解析:这道题可以画长方形图来具象化,长表示A,宽表示B,那么两数的积就是长方形的面积。
A、B原来两数用长方形图a表示,当A增加12即长增加12,宽不变,即B不变,如图b;当B增加12即宽增加12,长不变,也就是A不变,如图c。
所以:长方形的宽也就是B=72÷12=6,长方形的长也就是A=120÷12=10,那么,A、B的积为6×10=60。
立体图法例:把一个正方体切成两个长方体,表面积就增加了8平方米。
原来正方体的表面积是多少平方米?根据题意作图:解析:由图可知,增加的8平方米,就是正方体的2个面,每个面的面积是8÷2=4(平方米),则正方体的表面积是:4×6=24(平方米)。
列表图法例:有一个5分币,4个2分币,8个1分币。
要拿9分钱,有几种拿法?根据题意作图:由列表图,可以清楚看到共有7种拿法。
树状图法例:小明是个小马虎,晚上睡觉时将两双不同的袜子放在床头,早上起床没看清就随便穿了两只。
小明正好穿的是同一双袜子的可能性是多少?解析:假设2双袜子为A袜、B袜,那么4只袜子分别是A1、A2、B1、B2,根据题意作图:由树状图可知,2双袜子任意搭配有12种情况,其中同一双的情况有4种,所以小明穿同一双袜子的的可能性是4/12,也就是1/3。
小学数学典型应用题之画图法解鸡兔同笼一、含义鸡兔同笼是中国古代的数学名题之一。
大约在1500年前,《孙子算经》中就记载了这个有趣的问题。
书中是这样叙述的:“今有雉兔同笼,上有百头,雉足多兔足二十六,问雉兔各几何?”这四句话的意思是:有若干只鸡兔同在一个笼子里,从上面数,有100个头,从下面数,鸡的脚比兔子的脚多26只。
问笼中各有几只鸡和兔?二、解题思路和方法在解题时,会遇到一些较难的题目,这时可用画图的方法把题目中的条件画出来再思考,往往会容易得多。
在有些数学题中,数量之间的关系不容易看出来。
而画图却能比较清楚地显示出来,所以在解决鸡兔同类问题时也可以利用画图法进行求解,以便于提高做题的效率。
三、例题例题(一):鸡、兔关在同一笼子里,共有10个头,28条腿,请问笼里有几只鸡?几只兔?解析:(1)我们用“○”来表示头,因此要画10个“○”,用“|”表示腿,那么鸡有两条腿,兔子有四条腿,所以鸡的腿数比兔子的少。
(2)先全画成鸡,可得到下图:(3)从图中可以看出,10只鸡只有20条腿,而条件说“共有28条腿”,因此少了28-20=8条腿。
(4)所以需要在图上,给鸡加上两条腿,把它变成兔子,那么8条腿添改4次即可。
如下图:(5)所以由图可得:笼里有4只兔,6只鸡。
例题(二):一只蛐蛐6条腿,一只蜘蛛8条腿。
现在有蛐蛐和蜘蛛共10只,其共有68条腿,那么请问蛐蛐和蜘蛛各有多少只?解析:(1)用“○”来表示头,但由于蛐蛐和蜘蛛的腿比较多,画“|”不方便,所以就可以用数字表示,写在头的下面。
先把它们看成是腿较少的动物——蛐蛐。
可以画出下图:(2)从图中可以看出,10只蛐蛐共有60条腿,比已知条件少了68-60=8条腿。
(3)而一只蜘蛛比一只蛐蛐多条腿,因此8条腿只需改成4只蛐蛐就可以了。
如下图:(4)即共有6只蛐蛐和4只蜘蛛。
例题(三):一辆自行车有2个轮子,一辆三轮车有3个轮子。
车棚里放着自行车和三轮车共8辆,共20个轮子。
作图法解题专题分析:用作图法把应用题的数量关系表示出来,使题意形象具体,一目了然,以便较快地找到解题的途径,它对解答条件隐蔽、复杂疑难的应用题,能起化难为易的作用。
在解答已知一个数或者几个数的和差、差倍以及相互之间的关系、求其中一个数或者几倍数问题等应用题时,我们可以抓住题中给出的数量关系,借助线段图进行分析,从而列出算式。
【经典例题】例1、五(一)班的男生人数和女生人数同样多。
抽去18名男生和26名女生参加合唱团,剩下的男生人数是女生的3倍。
五(一)班原有男女生多少人?☆☆☆☆练习一:1、两根电线一样长,第一根剪去50厘米,第二根剪去180厘米后,剩下部分,第一根是第二根长度的3倍。
这两根电线原来共长多少厘米?2、甲乙两筐水果个数一样多,从第一筐中取出31个,第二筐中取出19个后,第二筐剩下的个数是第一筐的4倍。
原来两筐水果各有多少个?3、哥哥现存的钱是弟弟的5倍,如果哥哥再存20元,弟弟再存100元。
二人的存款正好相等。
哥哥原来存有多少钱?例2、两根电线共长59米,如果第一根剪去3米,第一根电线的长度就是第二根的3倍。
求原来两根电线各长多少米?练习二:1、甲乙两筐苹果共重83千克,如果从甲筐取出3千克后,甲筐苹果的重量就是乙筐的4倍。
甲乙两筐苹果原来各重多少千克?2、学校图书室共有图书和故事书250本,又买来50本科技书后,科技书的本数是故事书的2倍,学校图书馆原来各有科技书和故事书多少本?3、参加奥数竞赛集训的男生和女生共有21人,如果女生减少5名,男生人数就是女生的3倍,参加奥数竞赛集训的男女生各有多少人?例3、甲乙丙丁四个小组的同学共植树45棵,如果甲组多植2棵,乙组少植2棵,丙组植的棵数扩大2倍丁组植树减少一半,那么四个组植的树正好相同。
原来四个小组各植树多少棵?练习三:1、甲乙丙丁四个数的和是100,甲数加上4,乙数减去4,丙数乘以4,丁数除以4,四个数正好相等,求这四个数。
2、甲乙丙三人分113个苹果,如果把甲分得个数减去5,乙分得的个数减去24,丙把分得的个数送给别人一半后,三人的苹果个数相同。
画图法解应用题
例1.朗诵小组的同学排成一排表演诗朗诵,从左边数起,玲玲是第8个,从右边数起,玲玲是第7个,有多少个同学参加表演?
随堂练习1.排排队,来报数,正着报数我报6,倒着报数我报9,请你算一算,一共有多少个小朋友在报数?
例2.16名同学排成一队,小小排在小亚的前面,从前往后数,小亚排在第9个,从后往前数,小小排在第10个。
他们之间隔着几个人?
随堂练习2.16个小朋友排成一队去看电影,胖胖在小明的后面,从前往后数,小明排在第5个,从后往前数,胖胖排在第8个,小明和胖胖之间隔了几个人?
例3.小明有10支铅笔,小红有4支铅笔,要使两人的铅笔同样多,小明要给小红几支铅笔?
随堂练习3.王老师有12本练习本,李老师有18本练习本,要使两人的练习本同样多,李老师要给王老师多少本练习本?
例4.一排20个座位,其中有些座位已经有人,小明无论坐在哪一个座位上,旁边都有一个人与他相邻,那么原来至少有多少人已经就座?
随堂练习4.一排10个座位,其中有些座位已经有人,小刚无论坐在哪一个座位上,旁边都有一个人与他相邻,那么原来至少有几个人已经就座?
例5.如图,一条小街上顺次安装有10盏路灯,为了节约用电又不影响路面照明,要关闭除首末两盏灯以外的8盏灯中的4盏灯,但被关的灯不能相邻。
一共有几种不同的关法?
随堂练习5.把4个一样的球放到两个相同的盒子里,有多少种不同的方法?
练习题
1.二(1)班22个小朋友排成一队去操场做操,从最前面数到丁丁是第9个,君君排在丁丁的后面,从
队伍的最后往前数,君君排在第几个?
2.第一小队的同学排成一排,排在东东前面的有6个小朋友,排在东东后面的有4个小朋友。
第一小队
一共有几个小朋友?
3.小朋友们排成一队去参观博物馆,从排头数起牛牛是第10个,从排尾数起妞妞是第18个,排在牛牛
前面的就是妞妞。
一共有几个小朋友去参观博物馆?
4.在20米的校园小道一边种杨柳树,每隔4米种一棵,两端都种。
想一想,一共要种几棵树?
5.小明给小红4支铅笔后,两人的支数相同,问:小明比小红多几支铅笔?
6.姐姐有4支铅笔,妹妹给姐姐3支铅笔后,两人的支数相同,妹妹原来有几支铅笔?
7.一根16米长的木条,把它锯成4段,要锯几次?
8.小丁从一楼走到四楼用了9分钟,照这样的速度,从一楼走到七楼要用几分钟?
9.妈妈到水果店买苹果,她带的钱若买3千克多2元,若买4千克少3元,问妈妈带了多少钱去买苹果?
10.体育小组有20个学生,排成两排队伍做早操,每两个学生之间相隔1米,每排队伍有多长?。