环路稳定性分析

用示波器测试电源环路稳定性的方法首先开关电源的环路补偿基础知识内容涉及广，需要的数理知识比较庞杂。

1、反馈控制系统开关电源是一种典型的反馈控制系统，其有响应速度和稳定性两个重要的指标。

响应速度就是当负载变化或者输入电压变化时，电源能迅速做出调整的速度。

因为开关电源的负载多数情况下都是数字IC，其电流会随着逻辑功能的变化而变化，比如FPGA在进行配置时，电流会增大一倍以上。

而开关电源的输入电压也会有一定程度的波动。

为了保证电源稳定输出，不产生跌落或者过冲，就要求电源必须迅速做出调整，使得最终输出的电压没有变化。

而电源的响应速度就决定了电源的调整速度。

由于电源加入了反馈系统，就可能发生震荡。

如果电源系统的参数没有设置好，就会产生震荡，结果就是电压上会被叠加一个固定频率的波动。

导致电源不稳定。

开关电源如下图所示：从开关电源的框图中可以看出，该系统是通过一个反馈电路，将最终输出的变化反馈给比例电路，经过比例电路的等比例衰减，输入到误差放大器中。

而后误差放大器通过比较该信号和内部参考信号的差异，来驱动后级脉宽调制器等一系列的输出环节，最终与干扰信号相互抵消，从而保证电源的稳定。

2、波特图幅度曲线的频率响应是电压增益改变与频率改变的关系,这种关系可以用波特图上一条以分贝(dB)来表示的电压增益比频率(Hz)曲线来描述.波特幅度图被绘成一种半对数曲线:x轴为采用对数刻度的频率(Hz),y轴则为采用线性刻度的电压增益(dB),波特图的另一半则是相位曲线(相移比频率),并被描述成以”度”来表示的相移比频率关系.波特相位曲线亦被绘成一种半对数曲线:x轴为采用对数刻度的频率(Hz),y轴为采用线性刻度的相移(度)。

很多同学容易把波特图看不明白，是因为用一个坐标系，把增益和相位画到一张图上，导致的认知错乱。

如下图，注意左边纵坐标是增益，单位是dB；右边的纵坐标是相位，单位是°。

横坐标是频率，是两个变量曲线共用的。

运放稳定性分析环路稳定性基础引言本系列所采用的所有技术都将“以实例来定义”,而不管它在其他应用中能否用普通公式来表达。

为便于进行稳定性分析,我们在工具箱中使用了多种工具,包括数据资料信息、技巧、经验、SPICE仿真以及真实世界测试等,都将用来加快我们的稳定运放电路设计。

尽管很多技术都适用于电压反馈运放,但上述这些工具尤其适用于统一增益带宽小于20MHz的电压反馈运放。

选择增益带宽小于20MHz的原因是,随着运放带宽的增加,电路中的其他一些主要因素会形成回路,如印制板(PCB) 上的寄生电容、电容中的寄生电感以及电阻中的寄生电容与电感等。

我们下面介绍的大多数经验与技术并非仅仅是理论上的,而且是从利用增益带宽小于20MHz的运放、实际设计并构建真实世界电路中得来的。

本系列的第1部分回顾了进行稳定性分析所需的一些基本知识,并定义了将在整个系列中使用的一些术语。

波特图（曲线）基础幅度曲线的频率响应是电压增益改变与频率改变的关系。

这种关系可用波特图上一条以分贝(dB) 来表示的电压增益比频率(Hz) 曲线来描述。

波特幅度图被绘成一种半对数曲线：x轴为采用对数刻度的频率(Hz)、y轴则为采用线性刻度的电压增益(dB) ,y轴最好是采用方便的每主格45°刻度。

波特图的另一半则是相位曲线（相移比频率）,并被描绘成以“度”来表示的相移比频率关系。

波特相位曲线亦被绘成一种半对数曲线：x轴为采用对数刻度的频率(Hz)、y轴为采用线性刻度的相移（度）,y轴最好是采用方便的每主格45°刻度。

幅度波特图要求将电压增益转换成分贝(dB) 。

进行增益分析时,我们将采用以dB（定义为20Log10A）表示的电压增益,其中A为以伏/伏表示的电压增益。

在电压增益波特图上,增益随频率变化的斜线可定义成按+20dB/decade或-20dB/decade增加或减小。

另一种描述同样斜线的方法是按+6dB/octave 或-6dB/octave增加或减小（参见图1.4）以下推导证明了20dB/decade与6dB/octave的等效性：?A(dB) = A(dB) at fb – A(dB) at fa?A(dB) = [Aol(dB) - 20log10(fb/f1)] – [Aol(dB) - 20log10(fa/f1)]?A(dB) = Aol(dB) - 20log10(fb/f1) – Aol(dB) + 20log10(fa/f1)]?A(dB) = 20log10(fa/f1) – 20Log10(fb/f1)]?A(dB) = 20log10(fa/fb)?A(dB) = 20log10(1k/10k) = -20dB/decade?A(dB) = 20log10(fb/fc)?A(dB) = 20log10(10k/20k) = -6db/octave-20dB/decade = -6dB/octave因此：+20dB/decade = +6dB/octave -20dB/decade = -6dB/octave+40dB/decade = +12dB/octave -40dB/decade = -12dB/octave+60dB/decade = +18dB/Octave -60dB/decade = -18dB/Octave极点à单个极点响应在波特图（幅度或增益曲线）上具有按-20dB/decade 或-6db/octave斜率下降的特点。

典型的两级运算放大器环路稳定性分析典型的两级运放如图所示，负载电容CL=50fF。

首先建立静态工作点。

加偏置电流I0=4uA,加共模输入电平1.25V。

仿真后得到结果如下，静态工作点是合适的。

1.开环分析米勒补偿前做开环分析如下，显然，这是不合适的。

加米勒补偿电容Cc=200fF，做开环分析如下，显然，这也是不合适的。

这是由于电路中存在零点造成的。

加入调零电阻Rz=40K，，仿真结果如下。

可以看出，，，相位裕度为40度，不够。

可通过加大补偿电容来进一步分裂p1，p2主次极点。

（已尝试过加米勒补偿电容Cc=300fF可以得到大于60度的相位裕度）。

但是本次设计的运放用在负反馈环路中，故只需要负反馈环路是稳定的就达到设计标准。

理论计算。

查看各管子的静态工作点。

，，，即。

，，，即。

，。

理论值与仿真结果非常接近。

，理论值与仿真结果非常接近。

，，理论值与仿真结果非常接近。

，，理论值与仿真结果40度偏差较大。

2.在负反馈环路中做环路稳定性分析：从上图可以看出，加入反馈电阻网络R1，R2后就打破了原有的静态工作点：主要是反馈电阻网络R1，R2中的电流由M7管提供，所以M7管的静态工作点打破了，即运放的第二级跨导GmⅡ，输出电阻R2都变了。

从波特图中可以看出相位裕度为77度，满足设计标准。

理论计算：查看各管子的静态工作点。

，，，即。

，，，即。

，。

理论值与仿真结果非常接近。

，理论值与仿真结果非常接近。

，理论值与仿真结果非常接近。

，，理论值与仿真结果77度偏差较大。

此结果可能是由于gm7变大，原来的调零电阻RZ过大造成的。

现在改变调零电阻Rz=25K，，仿真结果如下：此时，相位裕度为63度，满足设计标准。

3.改用大电感大电容仿真环路增益：仿真方法如上图所示，将环路断开，加入大电感L0=1GH通直流以建立直流工作点，并且断开交流通路，加入大电容C3=1GF通交流小信号V8。

从仿真结果图中可以看出相位裕度为70度。

不同的仿真方式所得到的结果略有误差。

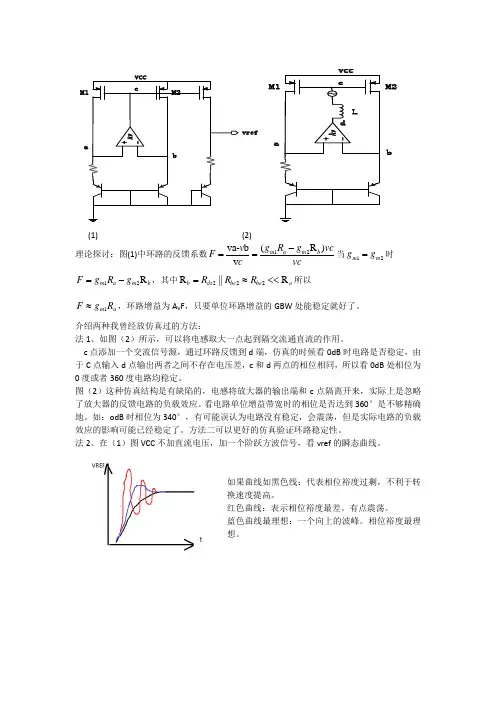
vrefbM2(1) (2)理论探讨：图(1)中环路的反馈系数12(R)va-bvm a m bg R g vcvFc vc-==当12m mg g=时12Rm a m bF g R g=-，其中222R||Rb ds be be aR R R=≈<<所以1m aF g R≈，环路增益为A V F，只要单位环路增益的GBW处能稳定就好了。

介绍两种我曾经放仿真过的方法：法1、如图（2）所示，可以将电感取大一点起到隔交流通直流的作用。

c点添加一个交流信号源，通过环路反馈到d端，仿真的时候看0dB时电路是否稳定，由于C点输入d点输出两者之间不存在电压差，c和d两点的相位相同，所以看0dB处相位为0度或者360度电路均稳定。

图（2）这种仿真结构是有缺陷的，电感将放大器的输出端和c点隔离开来，实际上是忽略了放大器的反馈电路的负载效应。

看电路单位增益带宽时的相位是否达到360°是不够精确地。

如：odB时相位为340°，有可能误认为电路没有稳定，会震荡，但是实际电路的负载效应的影响可能已经稳定了。

方法二可以更好的仿真验证环路稳定性。

法2、在（1）图VCC不加直流电压，加一个阶跃方波信号，看vref的瞬态曲线。

如果曲线如黑色线：代表相位裕度过剩，不利于转换速度提高。

红色曲线：表示相位裕度最差。

有点震荡。

蓝色曲线最理想：一个向上的波峰。

相位裕度最理想。

开关电源环路稳定的实验方式方法6.5 开关电源环路稳定的试验方法前面频率特性分析方法是以元器件小信号参数为基础，同时在线性范围内，似乎很准确。

但有时很难做到，例如电解电容ESR不准确且随温度和频率变化；电感磁芯磁导率不是常数，还有由于分布参数或工艺限制，电路存在分布参数等等，使得分析结果不可能完全吻合，有时甚至相差甚远。

分析方法只是作为实际调试的参考和指导。

因此，在有条件的情况下，直接通过测量运算放大器以外的环路的频率响应，根据6.4节的理论分析，利用测得的频率特性选择Venable误差放大器类型，对环路补偿，并通过试验检查补偿结果，应当说这是最直接和最可靠设计方法。

采用这个方法，你可以在一个星期之内将你的电源闭环调好。

前提条件是你应当有一台网络分析仪。

6.5.1 如何开环测试响应桥式、半桥、推挽、正激以及Buck变换器都有一个LC滤波电路，输出功率电路对系统性能影响最大。

为了讨论方便，以图6.31为例来说明测试方法，重画为图6.48(a)。

电路参数为：输入电压115V，输出电压为5V，如前所述，滤波电感和电容分别为L=15μH，C=2600μF，PWM控制器采用UC1524,它的锯齿波幅值为3V，只用两路脉冲中的一路，最大占空比为0.5。

为了测量小信号频率特性，变换器必须工作在实际工作点：额定输出电压、占空比和给定的负载电流。

从前面分析知道，如果把开关电源看着放大器，放大器的输入就是参考电压。

从反馈放大器电路拓扑来说，开关电源的闭环是一个以参考电压为输入的电压串联负反馈电路。

输入电源的变化和/或负载变化是外界对反馈控制环路的扰动信号。

取样电路是一个电阻网络的分压器，分压比就是反馈系数，一般是固定的（R2/(R1+R2)）。

参考电压（相应于放大器的输入电压）稳定不变，即变化量为零，输出电压也不变(5V)。

如上所述，所有三种误差放大器都有一个原点极点。

在低频闭环时，由于原点极点增益随频率减少而增高（即在反馈回路电容）在很低频率，有一个最大增益，由误差放大器开环增益决定。

多环路稳定性分析环路稳定性分析通常开始于一个正在研究的装置的开环伯德图。

例如一个Buck或者Flyback变换器的功率部分，从这张图中，设计者可以根据频率范围的变化得出相位和增益的数据。

他的工作是辨别一个交叉频率受相位余量影响的补偿器的结构，最后一步需要研究整个的环路增益在补偿器之后的功率装置一旦环路关断给出补偿器的零点极点以确保稳定。

如果这个过程是单环路的话实现Flyback 变换器加权的工作过程将会变得更加复杂。

本篇文章引用了参考文献1的工作同时探索不同的方法来提供技术给多反馈通道的功率变换器。

TL431 多环路系统单独一个431可以作为一个多通道反馈系统图1根据参考文献2给出了1种双结构的431典型的连线图图1 传统结构的431连线结构观察变换器的直流电压从这张原理图中看出可以看出所谓的低速和高速通道。

TL431可以被称为一个可调的齐纳管或者是分流调整器。

例如由于负载的变化，输出电压变化，这个信息通过R 2/R 3变换然后传递到TL431的输入端，令可调的齐纳管送出或者多或者少的电流进入光耦LED 。

通过调整它的阈值电压进而工作，利用这个方法，一次侧的反馈信号也改变，同时指导控制器调整工作点。

如果输出电压变化太快，通过电阻R 2感应到频率超越了由C 1引入的临界极点。

这时候，对于这个反馈信号通道的ac 补偿就失效了：TL431不再改变工作点、 LED 的阈值电压也就被固定。

然而，尽管LED 的阈值电压被固定，但是通过R LED ，阳极一直在感应着输出电压的变化，这个电流变化是通过光耦影响反馈电压。

因此，即使你增大C 1，对于环路的增益也没有什么影响。

因为R LED 一直在感应着输出电压，这样一个系统的传递公式可以写成如下两个所示的形式：()()()12111s FB OUT V S G S V S R C ⎡⎤=+⎢⎥⎣⎦ (1)这里G 1(S)表达通过光耦CTR ，LED 和连接在电容C 2上的提拉电阻带来的中间频带的增益，从这个表达式中，实际上我们通过解决公式1，可以看出两个环路的出现：()()()()1121s FB OUT V S G S G S V S R C =+ (2)这样一个系统的环路增益可以通过切断环路反馈工作点来测量。

典型的两级运算放大器环路稳定性分析典型的两级运算放大器环路稳定性分析典型的两级运放如图所示，负载电容CL=50fF 。

首先建立静态工作点。

首先建立静态工作点。

加偏置电流加偏置电流I0=4uA,加共模输入电平1.25V 。

仿真后得到结果如下，仿真后得到结果如下，静静态工作点是合适的。

态工作点是合适的。

1. 开环分析开环分析米勒补偿前做开环分析如下，显然，这是不合适的。

米勒补偿前做开环分析如下，显然，这是不合适的。

加米勒补偿电容Cc=200fF，做开环分析如下，显然，这也是不合适的。

这是由于电路中存在零点造成的。

存在零点造成的。

加入调零电阻Rz=40K，，仿真结果如下。

可以看出，，，相位裕度为40度，不够。

可通过加大补偿电容来进一步分裂p1，p2主次极点。

（已尝试过加米勒补偿电容Cc=300fF可以得到大于60度的相位裕度）。

但是本次设计的运放用在负反馈环路中，故只需要负反馈环路是稳定的就达到设计标准。

运放用在负反馈环路中，故只需要负反馈环路是稳定的就达到设计标准。

理论计算。

理论计算。

查看各管子的静态工作点。

查看各管子的静态工作点。

，，，即。

，，，即。

，非常接近。

理论值与仿真结果非常接近。

，理论值与仿真结果非常接近。

，非常接近。

，理论值与仿真结果非常接近。

，，理论值度偏差较大。

与仿真结果40度偏差较大。

2.在负反馈环路中做环路稳定性分析：在负反馈环路中做环路稳定性分析：从上图可以看出，加入反馈电阻网络R1，R2后就打破了原有的静态工作点：主要是反馈电阻网络R1，R2中的电流由M7管提供，所以M7管的静态工作点打破了，即运放的第二级跨导GmⅡ，输出电阻R2都变了。

从波特图中可以看出相位裕度为77度，满足设计标准。

理论计算：理论计算：查看各管子的静态工作点。

查看各管子的静态工作点。

，，，即。

，，，即。

，非常接近。

，理论值与仿真结果非常接近。

，理论值与仿真结果非常接近。

，此时，相位裕度为63度，满足设计标准。

环路稳定性分析范文环路稳定性分析是指对系统的闭环控制回路进行稳定性评估的一种方法。

在控制系统中，闭环控制回路的稳定性是一个至关重要的指标，它决定了系统的性能和可靠性。

在本文中，我将介绍环路稳定性的概念、常见的分析方法以及如何通过稳定性分析来优化系统的闭环控制回路。

闭环控制回路由控制器、系统和反馈组成。

控制器接收反馈信号，并根据系统的输出进行调整，以使系统的输出接近期望值。

为了确保控制系统的稳定性，必须满足闭环控制回路的极点位置位于左半平面。

根轨迹法是一种通过绘制系统的开环传递函数极点随控制器参数变化的路径来评估系统的稳定性的方法。

通过绘制根轨迹图，可以直观地观察系统的极点位置，从而判断系统是否稳定。

根轨迹法还可以通过调整控制器参数来优化系统的闭环控制回路。

频域法是一种使用频率响应函数来分析系统稳定性的方法。

通过将系统的传递函数表示为复频域上的表达式，我们可以使用频率响应函数来分析系统的频率特性和稳定性。

常见的频域法包括振荡饱和法和Bode图法。

这些方法可以用来评估系统的衰减比、相位裕度和增益裕度等指标，从而判断系统的稳定性。

状态空间法是一种使用系统的状态方程来分析稳定性的方法。

通过求解系统状态方程的特征根，可以判断系统的稳定性。

状态空间法是一种更为准确和全面的稳定性分析方法，它可以考虑系统的所有状态变量，并提供系统的详细动态特性信息。

在进行环路稳定性分析时，我们通常关注系统的相位裕度、增益裕度和衰减比等指标。

相位裕度是指系统的相位与临界相位之间的差距，是评估系统稳定性的重要指标。

增益裕度是指系统增益与临界增益之间的差距，也是判断系统稳定性的重要依据。

衰减比是指系统在闭环控制下输出与输入的幅值比值，它可以通过计算系统的频率响应函数来得到。

对于不稳定的系统，我们可以通过调整控制器参数、增加补偿网络或采取其他控制策略来提高系统的稳定性。

例如，可以通过增加比例增益、增加积分时间常数或增加滤波器来提高系统的稳定性。

开关电源环路增益相位裕量测量与稳定性分析摘要：本文从小信号的角度来看通过对反馈环路注入一扰动信号对整个产品造成的影响，来衡量产品的稳定性，再利用环路分析仪检测环路做定量的分析，其结果以便于日后工作的改进，从而提高产品的可靠性。

关键词：反馈环路、带宽、相位裕量、增益裕量、稳定性、PSM1700、过零点title: a mearurement of swtich power supply based on FRAABSTRACT:THIS article describes the affection to the whole product, which is because of injecting a perturbation signal into feedback loop,to evaluate the stability, then by the use the frequency response analyzer equepiment gets an accurate result ,and the result is used for improvement ,as well as improve the products' reliablity.keywords:feedback loop bandwidth phase margin gain margin stablity随着电子，自控，航天，通讯，医疗器械等技术不断向深度和广度的发展，势必要求为其供电的电源要有更高的稳定性，即不仅要有好的线性调节率、负载调节率还要有快速的动态负载响应。

而这些因素都和控制环路有关，控制环路一般工作在负反馈状态，称之为电压负反馈。

如果变换器中没有用到反馈控制环路（即下图1中H部分），其传递函数一般为其中G为输入滤波、功率变换、整流滤波部分等因数的乘积（因为其为级联的形式，所以本文中以总的乘积因子G来表示），可以看出输出随着输入的变化而成线性的变化，但是由于整流、滤波网络在整个时域的非线性，实际上这种变化应该是近似于线性，所以当输入电压改变的时候并不能很好的起到稳压的作用；如果反馈环路设计的不好，对于负载的瞬态改变，环路不能做出及时恰当的调整，那么输出电压瞬间会偏高或者偏低，甚至有可能造成电源系统的振荡，对下一级构成损坏。

环路稳定的判断依据
环路稳定的判断依据主要包括两个方面，极点位置和频率响应。

首先，极点位置是判断系统稳定性的重要依据之一。

在控制系统中，系统的极点位置决定了系统的动态响应特性。

当系统的极点全部位
于左半平面时，系统是稳定的；而当系统的极点存在于右半平面时，系统就是不稳定的。

因此，通过分析系统的极点位置，我们可以初
步判断系统的稳定性。

其次，频率响应也是判断系统稳定性的重要依据之一。

频率响
应描述了系统对不同频率输入信号的响应特性，通过频率响应分析，我们可以了解系统在不同频率下的增益和相位特性。

在频率响应分
析中，我们通常会使用频率域工具，如波特图和Nyquist图等，来
评估系统的稳定性。

通过分析系统的频率响应，我们可以进一步确
认系统的稳定性和性能。

除了极点位置和频率响应外，还有一些其他判断依据，如阶跃
响应、脉冲响应等，这些都可以帮助我们更全面地评估系统的稳定
性和性能。

综上所述，环路稳定的判断依据是多方面的，需要综合考虑系
统的极点位置、频率响应以及其他动态特性。

在控制系统的设计和分析中，我们需要充分利用这些判断依据，以确保系统能够稳定地工作，并满足性能要求。

在Buck 电路中，环路稳定准则主要取决于控制策略和系统参数。

下面列举了一些常用的环路稳定准则：
1. 负反馈环路稳定性：对于负反馈环路，其稳定性取决于反馈增益和输入信号的频率。

当反馈增益大于1 且输入信号的频率足够高时，负反馈环路是稳定的。

此外，根据Bode 图分析，反馈增益的相位裕度也需要大于0°，以确保环路的稳定性。

2. 相位稳定准则：对于Buck 电路，输出电压与输入电压之间的相位差应保持在-90°至0°之间。

当相位差超过这个范围时，电路的稳定性会受到影响。

通过调整开关器件的导通和截止时间，可以实现输出电压与输入电压之间的相位调整，从而保证环路的稳定性。

3. 电压稳定准则：在Buck 电路中，输出电压的波动应控制在允许的范围内，以确保负载电压的稳定性。

通过调整控制策略和优化系统参数，可以实现电压的稳定控制。

4. 电流稳定准则：Buck 电路中的电流稳定性取决于负载电流的变化。

当负载电流发生波动时，通过调整开关器件的导通和截止时间，以及控制策略，可以实现电流的稳定输出。

5. 负载扰动抑制：在Buck 电路中，负载扰动会导致系统的不稳定。

为了提高环路的稳定性，需要采用负载电流前馈、补偿网络等方法来抑制负载扰动。

6. 控制策略：控制策略对于Buck 电路的稳定性至关重要。

常见的控制策略包括电压模式控制、电流模式控制、电压电流双模式控制等。

通过选择合适的控制策略并调整参数，可以实现Buck 电路的稳定运行。

环路稳定性基础引言本系列所采用的所有技术都将“以实例来定义”，而不管它在其他应用中能否用普通公式来表达。

为便于进行稳定性分析，我们在工具箱中使用了多种工具，包括数据资料信息、技巧、经验、SPICE仿真以及真实世界测试等，都将用来加快我们的稳定运放电路设计。

尽管很多技术都适用于电压反馈运放，但上述这些工具尤其适用于统一增益带宽小于20MHz的电压反馈运放。

选择增益带宽小于20MHz的原因是，随着运放带宽的增加，电路中的其他一些主要因素会形成回路，如印制板(PCB) 上的寄生电容、电容中的寄生电感以及电阻中的寄生电容与电感等。

我们下面介绍的大多数经验与技术并非仅仅是理论上的，而且是从利用增益带宽小于20MHz的运放、实际设计并构建真实世界电路中得来的。

本系列的第1部分回顾了进行稳定性分析所需的一些基本知识，并定义了将在整个系列中使用的一些术语。

图字（上、下）：数据资料信息、技巧、经验、Tina SPICE仿真、测试；目的：学习如何用数据资料信息、技巧、经验法则、Tina SPICE仿真及测试来“更容易地”分析和设计运放，以确保环路稳定性；注：用于统一增益带宽小于20MHz的电压反馈运放的技巧与经验法则。

波特图（曲线）基础幅度曲线的频率响应是电压增益改变与频率改变的关系。

这种关系可用波特图上一条以分贝(dB) 来表示的电压增益比频率(Hz) 曲线来描述。

波特幅度图被绘成一种半对数曲线：x轴为采用对数刻度的频率(Hz)、y轴则为采用线性刻度的电压增益(dB) ，y轴最好是采用方便的每主格45°刻度。

波特图的另一半则是相位曲线（相移比频率），并被描绘成以“度”来表示的相移比频率关系。

波特相位曲线亦被绘成一种半对数曲线：x轴为采用对数刻度的频率(Hz)、y轴为采用线性刻度的相移（度），y轴最好是采用方便的每主格45°刻度。

图字（上、下）：Aol曲线、幅度曲线、频率、相位曲线。

幅度波特图要求将电压增益转换成分贝(dB) 。

vrefbM2(1) (2)理论探讨：图(1)中环路的反馈系数12(R)va-bvm a m bg R g vcvFc vc-==当12m mg g=时12Rm a m bF g R g=-，其中222R||Rb ds be be aR R R=≈<<所以1m aF g R≈，环路增益为A V F，只要单位环路增益的GBW处能稳定就好了。

介绍两种我曾经放仿真过的方法：法1、如图（2）所示，可以将电感取大一点起到隔交流通直流的作用。

c点添加一个交流信号源，通过环路反馈到d端，仿真的时候看0dB时电路是否稳定，由于C点输入d点输出两者之间不存在电压差，c和d两点的相位相同，所以看0dB处相位为0度或者360度电路均稳定。

图（2）这种仿真结构是有缺陷的，电感将放大器的输出端和c点隔离开来，实际上是忽略了放大器的反馈电路的负载效应。

看电路单位增益带宽时的相位是否达到360°是不够精确地。

如：odB时相位为340°，有可能误认为电路没有稳定，会震荡，但是实际电路的负载效应的影响可能已经稳定了。

方法二可以更好的仿真验证环路稳定性。

法2、在（1）图VCC不加直流电压，加一个阶跃方波信号，看vref的瞬态曲线。

如果曲线如黑色线：代表相位裕度过剩，不利于转换速度提高。

红色曲线：表示相位裕度最差。

有点震荡。

蓝色曲线最理想：一个向上的波峰。

相位裕度最理想。