运放稳定性分析环路稳定性基础

典型的两级运算放大器环路稳定性分析典型的两级运放如图所示，负载电容CL=50fF。

首先建立静态工作点。

加偏置电流I0=4uA,加共模输入电平1.25V。

仿真后得到结果如下，静态工作点是合适的。

1.开环分析米勒补偿前做开环分析如下，显然，这是不合适的。

加米勒补偿电容Cc=200fF，做开环分析如下，显然，这也是不合适的。

这是由于电路中存在零点造成的。

加入调零电阻Rz=40K，，仿真结果如下。

可以看出，，，相位裕度为40度，不够。

可通过加大补偿电容来进一步分裂p1，p2主次极点。

（已尝试过加米勒补偿电容Cc=300fF可以得到大于60度的相位裕度）。

但是本次设计的运放用在负反馈环路中，故只需要负反馈环路是稳定的就达到设计标准。

理论计算。

查看各管子的静态工作点。

，，，即。

，，，即。

，。

理论值与仿真结果非常接近。

，理论值与仿真结果非常接近。

，，理论值与仿真结果非常接近。

，，理论值与仿真结果40度偏差较大。

2.在负反馈环路中做环路稳定性分析：从上图可以看出，加入反馈电阻网络R1，R2后就打破了原有的静态工作点：主要是反馈电阻网络R1，R2中的电流由M7管提供，所以M7管的静态工作点打破了，即运放的第二级跨导GmⅡ，输出电阻R2都变了。

从波特图中可以看出相位裕度为77度，满足设计标准。

理论计算：查看各管子的静态工作点。

，，，即。

，，，即。

，。

理论值与仿真结果非常接近。

，理论值与仿真结果非常接近。

，理论值与仿真结果非常接近。

，，理论值与仿真结果77度偏差较大。

此结果可能是由于gm7变大，原来的调零电阻RZ过大造成的。

现在改变调零电阻Rz=25K，，仿真结果如下：此时，相位裕度为63度，满足设计标准。

3.改用大电感大电容仿真环路增益：仿真方法如上图所示，将环路断开，加入大电感L0=1GH通直流以建立直流工作点，并且断开交流通路，加入大电容C3=1GF通交流小信号V8。

从仿真结果图中可以看出相位裕度为70度。

不同的仿真方式所得到的结果略有误差。

[转载]使用运放构成电压跟随器的稳定性问题[转载]使用运放构成电压跟随器的稳定性问题题外话：a：对于采用负反馈的放大电路，如何减少振荡以保持稳定，目前尚无定论。

电压跟随器也不例外。

（fig1.）运算放大器理想的运行状态是输出电压和输入电压为同相，即，当负输入端的印加电压引起输出增大时，运算放大器能够相应地使增加的电压降低。

不过，运算放大器的输入端和输出端的相位总有差异。

当输出和输出之间的相位相差180°时，负输入与正输入正好相同，原本应该减少的输出却得到了增强。

（成为正反溃的状态。

）如果在特定频段陷入这一状态，并且仍然保持原有振幅，那么该输出频率和振荡状态将一直持续下去。

fig1.电压跟随器和反馈环路2.输入输出端出现相位差的主要原因其原因大致可分为两种:1，由于运算放大器固有的特性2，由于运算放大器以外的反馈环路的特性2.1.运算放大器的特性fig2a及fig2b分别代表性地反映了运算放大器的电压增益—频率特性和相位—频率特性。

数据手册中也有这两张曲线图。

如图所示，运算放大器的电压增益和相位随频率变化。

运算放大器的增益与反馈后的增益（使用电压跟随器时为0db）之差，即为反馈环路绕行一周的增益（反馈增益）。

如果反馈增益不足1倍（0db），那么，即使相位变化180o，回到正反馈状态，负增益也将在电路中逐渐衰减，理论上不会引起震荡。

反而言之，当相位变化180o后，如频率对应的环路增益为1倍，则将维持原有振幅；如频率对应的环路增益为大于1倍时，振幅将逐渐发散。

在多数情况下，在振幅发散过程中，受最大输出电压等非线性要素的影响，振幅受到限制，将维持震荡状态。

为此，当环路增益为0db时的频率所对应的相位与180o之间的差是判断负反馈环路稳定性的重要因素，该参数称为相位裕度。

（fig2b.）如没有特别说明，单个放大器作为电压跟随器时，要保持足够相位裕度的。

注：数据手册注明「建议使用6ｄb以上的增益」的放大器，不可用作电压跟随器。

关于共模反馈环路稳定性的考虑 | Return To Innocence收藏人：mzsm2014-10-13 | 阅：转：| 来源| 分享在全差分运放的设计中，通常共模反馈的环路会比主运放的级数要多，这时共模反馈环路中多个极点会影响环路的稳定性，这里试着对此问题做些分析下图是一个简单的两级全差分放大器，其中的cmfb部分利用两个VCVS得到输出信号的共模，再与输入的Vcmo比较得到cmfb的反馈控制信号。

考虑共模反馈环路，其中存在3个极点，包括运放第一级的输出极点、第二级的输出极点以及cmfb节点对应的极点。

与分析运放稳定性问题一样，前两者分别为主极点和次主极点，对于第3个极点，由于其阻抗和输出极点一样在1/gm量级（实际上，为消除系统失调，运放输出共源放大的mos管和cmfb的二极管连接的mos管有相同的过驱动电压，其gm按w/l成比例），不能简单的忽略。

实际上，这个cmfb的极点与上图中P管的特征频率ft相关，为此我们需要为其选择一个合适的过驱动电压Vov:首先Vov不能太低，这样才能以保证其ft在足够高的频率，以避免cmfb极点对环路的作用；同时这Vov也不能太高，他必须提供一定的gm/Id，保证运放输出级在电流一定的条件下有足够的gm，从而避免运放输出极点频率的下降。

上面是对利用理想VCVS得到输出共模的方式下的一些分析，下面我们看看实际的得到输出共模电路中的问题。

以电阻方式等到输出信号的共模电平是一种常见的方法，如果忽略前面电路的输出阻抗，cm-sense的电阻Rs和之后的共模比较电路的栅节点电容Cx会在共模反馈的环路中引入一个极点。

考虑到一般Rs至少要在Rds量级以避免其对运放增益的衰减，这位个极点的位置不会太高，因此必须加以考虑。

实际中，可通过在电阻Rs上并联电容Cs来减小这一极点的影响。

在上面的电路中, 通过简单的分析, 可以得到: 引入 Cs 之后, 由 cm-sense 部分引入的零极点为: Po=1/(Rs*(Cs+Cx)), Zo=1/(Rs*Cs), 即在极点之后补了一个零点来抵消其作用. 至于具体的 Cs 的取值, 考虑 Cs 至少与 Cx 比较接近, cmfb 环路才能得到一定的相位裕度, 若进一步考虑零极点对建立时间的影响, 应该将 Cs/Cx 取为一定值以上才能将零极点拉的足够近, 以减小这一零极点对对共模信号建立时间的影响。

利用Pspice模型分析放大器环路的稳定性放大器放大器放大器的稳定性,但评估一个较为复杂的电路是否稳定，难度可能会大得多。

本文使用常见的Pspice宏模型结合一些简单的电路设计技巧来提高设计工程师的设计能力，以确保其设计的实用性与稳定性。

导致放大器不稳定的原因在任何相关频率下，只要环路增益不转变为正反馈，则闭环系统稳定。

环路增益是一个相量，因而具有幅度和相位特性。

环路由理想的负反馈转变为正反馈所带来的额外相移即是最常见的不稳定因素。

环路增益相位的＆ldquo;相关＆rdquo；频率，一般出现在环路增益大于或等于0dB之处。

图1：总等效噪声密度-反馈电阻关系曲线.的放大器电路,通过断开环路，测量信号在环路中传播一次所产生的相移，即可推算出电路的稳定情况.以下例子介绍的方法可利用仿真软件,运算放大器宏模型以及Pspice提供的理想元器件来实现。

图2:跨阻抗放大器。

高速低噪声跨阻放大器（TIA）稳定性示例我们以一个跨阻放大器（TIA）为例，通过分析其稳定性来阐述我们将要推荐的技术。

TIA广泛应用在工业领域和消费领域，例如LIDAR（光探测和测距)、条形码扫描仪、工厂自动化等。

设计工程师遇到的挑战是，在不会造成衰减和老化的情况下，如何最大化信噪比（SNR）,以及如何获得足够的速度/带宽来传递所需的信号.图2为采用了LMH6629的放大器示意图,这款超高速(GBWP=4GHz）低噪声(0。

69nV/RtHz)器件具有+10V/V的最小稳定增益（COMP引脚连至VCC)的。

LMH6629的补偿（COMP)输入可以连至VEE,从而进一步将最小稳定增益降低到4V/V。

为获得最大的转换速率和带宽（小信号和大信号）,在这个例子中,COMP引脚被连接到VCC。

可获得的带宽与放大器GBWP直接相关,与跨阻增益（RF）和光电二极管内的寄生电容成反比。

确定一个给定放大器所使用的反馈电阻（RF）有一个简单方便的办法:在使用了LMH6629的情况下,总等效输入电流噪声密度“ini&rdquo；与RF的关系.图中的＆ldquo；in＆rdquo；是LMH6629的输入噪声电流，＆ldquo;en”是LMH6629的输入噪声电压，&ldquo；k＆rdquo;是波尔兹曼常数,而&ldquo；T&rdquo；是用℃表示的绝对温度。

浅析DC/DC的环路稳定性问题
 在电路系统的单板设计中我们经常用到各种电源，DC/DC是最广泛的一种，比如BUCK降压电路，一般我们都采用的是相关厂家的集成芯片如TI、ADI、Linear等，总的来说应用还是比较简单的，按照参考电路配置外围器件即可，然后按照布局布线原则完成单板设计。

但是如果仅仅是知道基本原理却不知所以然，导致的结果就是在出现问题时完全摸不着头脑，比如最近遇到一个问题就是DC/DC在空载时电压异常的现象。

 这个问题是偶然出现的：该芯片已在其他单板上使用正常，但是最新的一块板子却出现电压异常波动。

对比二者原理图发现都一样，但是检查完PCB 后检查原理图发现输出电容配置有问题，改过电容后电压正常。

那幺为何同样的设计之前的没有问题，现在的有问题呢？进一步发现，新的问题板子在未使用时是空载的，而之前的板子都是一直带载，于是不改变电容插上负载，输出电压也正常了。

这是一个典型的开关电源的环路响应问题。

我们在学习运放的时候就研究过运放的闭环反馈特性，也就是幅频特性和相频特性。

 那幺对于DC/DC而言，环路同样具有类似特性，下图是一个同步BUCK 电路。

 基本的传输拓扑为：。

环路稳定性基础引言本系列所采用的所有技术都将“以实例来定义”，而不管它在其他应用中能否用普通公式来表达。

为便于进行稳定性分析，我们在工具箱中使用了多种工具，包括数据资料信息、技巧、经验、SPICE仿真以及真实世界测试等，都将用来加快我们的稳定运放电路设计。

尽管很多技术都适用于电压反馈运放，但上述这些工具尤其适用于统一增益带宽小于20MHz的电压反馈运放。

选择增益带宽小于20MHz的原因是，随着运放带宽的增加，电路中的其他一些主要因素会形成回路，如印制板(PCB) 上的寄生电容、电容中的寄生电感以及电阻中的寄生电容与电感等。

我们下面介绍的大多数经验与技术并非仅仅是理论上的，而且是从利用增益带宽小于20MHz的运放、实际设计并构建真实世界电路中得来的。

本系列的第1部分回顾了进行稳定性分析所需的一些基本知识，并定义了将在整个系列中使用的一些术语。

图字（上、下）：数据资料信息、技巧、经验、Tina SPICE仿真、测试；目的：学习如何用数据资料信息、技巧、经验法则、Tina SPICE仿真及测试来“更容易地”分析和设计运放，以确保环路稳定性；注：用于统一增益带宽小于20MHz的电压反馈运放的技巧与经验法则。

波特图（曲线）基础幅度曲线的频率响应是电压增益改变与频率改变的关系。

这种关系可用波特图上一条以分贝(dB) 来表示的电压增益比频率(Hz) 曲线来描述。

波特幅度图被绘成一种半对数曲线：x轴为采用对数刻度的频率(Hz)、y轴则为采用线性刻度的电压增益(dB) ，y轴最好是采用方便的每主格45°刻度。

波特图的另一半则是相位曲线（相移比频率），并被描绘成以“度”来表示的相移比频率关系。

波特相位曲线亦被绘成一种半对数曲线：x轴为采用对数刻度的频率(Hz)、y轴为采用线性刻度的相移（度），y轴最好是采用方便的每主格45°刻度。

图字（上、下）：Aol曲线、幅度曲线、频率、相位曲线。

幅度波特图要求将电压增益转换成分贝(dB) 。

运算放大器的稳定性4―环路稳定性主要技巧与经验运算放大器的稳定性第4部分（共15部分）：环路稳定性主要技巧与经验作者：Tim Green，TI公司本系列的第4部分着重讨论了环路稳定性的主要技巧与经验。

首先，我们将讨论45度相位及环路增益带宽准则，考察了在Aol 曲线与1/β曲线以及环路增益曲线Aolβ中的极点与零点之间的互相转化关系。

我们还将讨论用于环路增益稳定性分析的频率“十倍频程准则”。

这些十倍频程准则将被用于1/β、Aol及Aolβ曲线。

我们将给出运放输入网络ZI与反馈网络ZF的幅度“十倍频程准则”。

我们将开发一种用于在1/β曲线上绘制双反馈路径的技术，并将解释为何在使用双反馈路径时应该避免出现“BIG NOT”这种特殊情况。

最后，我们将给出一种便于使用的实际稳定性测试方法。

在本系列的第5部分中，这些关键工具的综合使用使我们能够系统而方便地稳定一个带有复杂反馈电路的实际运放应用。

环路增益带宽准则已确立的环路稳定性标准要求在fcl处相移必须小于180度，fcl是环路增益降为零时的频率。

在fcl处的相移与整个180度相移之间的差定义为相位余量。

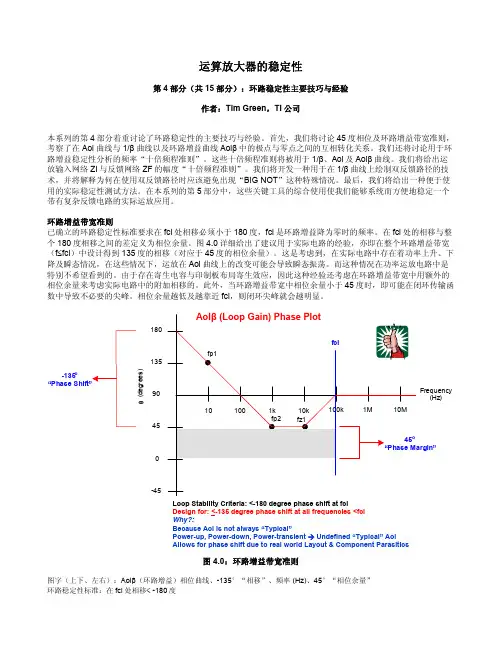
图4.0详细给出了建议用于实际电路的经验，亦即在整个环路增益带宽（f≤fcl）中设计得到135度的相移（对应于45度的相位余量）。

这是考虑到，在实际电路中存在着功率上升、下降及瞬态情况，在这些情况下，运放在Aol曲线上的改变可能会导致瞬态振荡。

而这种情况在功率运放电路中是特别不希望看到的。

由于存在寄生电容与印制板布局寄生效应，因此这种经验还考虑在环路增益带宽中用额外的相位余量来考虑实际电路中的附加相移的。

此外，当环路增益带宽中相位余量小于45度时，即可能在闭环传输函数中导致不必要的尖峰。

相位余量越低及越靠近fcl，则闭环尖峰就会越明显。

180135-135oFrequency90(Hz)450-45Loop Stability Criteria:<-180 degree phase shift at fcl -135 degree phase shift at all frequencies <fcl Why?: Because Aolis not always “Typical” Power-up, Power-down,Power-trans ient ?Undefined “Typical”Aol Allows for phase shift due to real world Layout & Component Parasitics图4.0：环路增益带宽准则图字（上下、左右）：Aolβ（环路增益）相位曲线、-135°“相移”、频率(Hz)、45°“相位余量”环路稳定性标准：在fcl处相移< -180度θ设计目的：在所有< fcl的频率上，都有相移≤-135度原因：因为Aol（开环增益）并不总是“典型”，考虑到实际电路布局与器件的寄生效应，存在着功率上升、下降及暂态现象→这些是未定义的“典型”Aol。

运算放大器的稳定性第4部分（共15部分）：环路稳定性主要技巧与经验作者：Tim Green，TI公司本系列的第4部分着重讨论了环路稳定性的主要技巧与经验。

首先，我们将讨论45度相位及环路增益带宽准则，考察了在Aol 曲线与1/β曲线以及环路增益曲线Aolβ中的极点与零点之间的互相转化关系。

我们还将讨论用于环路增益稳定性分析的频率“十倍频程准则”。

这些十倍频程准则将被用于1/β、Aol及Aolβ曲线。

我们将给出运放输入网络ZI与反馈网络ZF的幅度“十倍频程准则”。

我们将开发一种用于在1/β曲线上绘制双反馈路径的技术，并将解释为何在使用双反馈路径时应该避免出现“BIG NOT”这种特殊情况。

最后，我们将给出一种便于使用的实际稳定性测试方法。

在本系列的第5部分中，这些关键工具的综合使用使我们能够系统而方便地稳定一个带有复杂反馈电路的实际运放应用。

环路增益带宽准则已确立的环路稳定性标准要求在fcl处相移必须小于180度，fcl是环路增益降为零时的频率。

在fcl处的相移与整个180度相移之间的差定义为相位余量。

图4.0详细给出了建议用于实际电路的经验，亦即在整个环路增益带宽（f≤fcl）中设计得到135度的相移（对应于45度的相位余量）。

这是考虑到，在实际电路中存在着功率上升、下降及瞬态情况，在这些情况下，运放在Aol曲线上的改变可能会导致瞬态振荡。

而这种情况在功率运放电路中是特别不希望看到的。

由于存在寄生电容与印制板布局寄生效应，因此这种经验还考虑在环路增益带宽中用额外的相位余量来考虑实际电路中的附加相移的。

此外，当环路增益带宽中相位余量小于45度时，即可能在闭环传输函数中导致不必要的尖峰。

相位余量越低及越靠近fcl，则闭环尖峰就会越明显。

18013545Frequency(Hz)90θ-45-135oDesign for: <Loop Stability Criteria:<-180 degree phase shift at fcl-135 degree phase shift at all frequencies <fclWhy?:Because Aol is not always “Typical”Power-up, Power-down, Power-transient ÆUndefined “Typical”AolAllows for phase shift due to real world Layout & Component Parasitics图4.0：环路增益带宽准则图字（上下、左右）：Aolβ（环路增益）相位曲线、-135°“相移”、频率 (Hz)、45°“相位余量”环路稳定性标准：在fcl处相移< -180度设计目的：在所有< fcl 的频率上，都有相移≤ -135度原因：因为Aol （开环增益）并不总是“典型”，考虑到实际电路布局与器件的寄生效应，存在着功率上升、下降及暂态现象→这些是未定义的“典型” Aol 。

运放稳定性第1部分（共15部分）：环路稳定性基础作者：Tim Green ，TI 公司Burr-Brown 产品战略发展经理1.0 引言本系列所采用的所有技术都将“以实例来定义”，而不管它在其他应用中能否用普通公式来表达。

为便于进行稳定性分析，我们在工具箱中使用了多种工具，包括数据资料信息、技巧、经验、SPICE 仿真以及真实世界测试等，都将用来加快我们的稳定运放电路设计。

尽管很多技术都适用于电压反馈运放，但上述这些工具尤其适用于统一增益带宽小于20MHz 的电压反馈运放。

选择增益带宽小于20MHz 的原因是，随着运放带宽的增加，电路中的其他一些主要因素会形成回路，如印制板 (PCB) 上的寄生电容、电容中的寄生电感以及电阻中的寄生电容与电感等。

我们下面介绍的大多数经验与技术并非仅仅是理论上的，而且是从利用增益带宽小于20MHz 的运放、实际设计并构建真实世界电路中得来的。

本系列的第1部分回顾了进行稳定性分析所需的一些基本知识，并定义了将在整个系列中使用的一些术语。

9Data Sheet Info 9Tricks 9Rules-Of-Thumb 9Tina SPICE Simulation9TestingGoal:EASILY Tricks & Rules-Of-Thumb apply for Voltage FeedbackOp Amps, Unity Gain Bandwidth <20MHzTo learn how to analyze and design Op Amp circuits for guaranteed Loop Stability using Data Sheet Info, Tricks, Rules-Of-Thumb, Tina SPICE Simulation, and Testing.Note:图1.0 稳定性分析工具箱图字（上、下）：数据资料信息、技巧、经验、Tina SPICE 仿真、测试；目的：学习如何用数据资料信息、技巧、经验法则、Tina SPICE 仿真及测试来“更容易地”分析和设计运放，以确保环路稳定性；注：用于统一增益带宽小于20MHz 的电压反馈运放的技巧与经验法则。

共模反馈环路稳定性分析及电路设计
0 引言
全差分运放(fully differential operation)相对于单端输出电路来说，不仅输出摆幅更大、共模噪声抑制更好，还能消除高阶谐波失真。

然而，在高增益运放中，输出共模电平对器件的特性和失配相当敏感，而且不能通过差模反馈来达到稳定。

因此，必须额外引入负反馈机制，即共模反馈(CMFB)来稳定运放
的共模输出电平。

共模反馈的基本原理是先通过检测网络得到输出共模电平
Vo_cn，然后将Vo_cn 和一个参考电压Vcn(一般为电源电压的一半)相比较，再用得出的误差信号来调节运放的偏置电流，从而达到使输出共模信号稳定的目的。

这种方式的设计要点如下：
(1)共模信号检测应具有线性特性；
(2)共模反馈环路的增益必须尽可能的高；
(3)反馈环路的带宽不能小于差模通路(在许多实际应用中，这两个带宽
必须一致)；
(4)确保共模环路稳定；
(5)应引入保护机制，以避免锁死状态的出现(输出保持在电源电压的情况)。

目前已经有了大量关于差模反馈环路稳定性的理论研究，而对于共模反馈环路的研究却很少。

现有的共模反馈电路的设计更多的是通过实际经验、反复调试来得到稳定环路。

笔者通过对最常用的、采用一级共模反馈的两级运放的环路进行稳定性分析，明确得出了其稳定条件，从而理论化了共模反馈电路的设计。

然后基于这个条件，并采用Bi-CMOS 工艺设计了一种低成本、高稳定、匹配好的共模反馈电路。

整个运放可应用于一款高性能音频CLASS-D 芯。

1目的 (2)2适用范围 (2)3引用标准 (2)4测试仪器/设备 (2)5定义 (2)5.1环路稳定性 (2)5.2相位裕度 (2)5.3增益裕度 (2)5.4穿越频率 (2)6环路稳定性评价方法 (3)6.1环路稳定性评价指标 (3)6.2开关电源控制环路稳定性验证 (3)6.3环路稳定性评价指标判定 (3)7附录 (4)1目的制定日期页码第2 / 4页本规范为产品验证阶段的环路稳定性测试提供指导，保证正确测量环路特性和合理评估电源产品的稳定程度。

2适用范围本规范适用于MOS 消费类电源和LED 电源验证过程中进行的电路环路稳定性评价。

3引用标准无4测试仪器/设备N4L PSM2200频率响应分析仪5、定义5.1环路稳定性：是评价电源输出电压品质的一项重要指标，即直接决定电源启动特性、输入电压跃变响应 特性、负载跃变响应特性、高低温稳定性以及影响生产和调试难易度等的特性。

5.2增益裕度(Gain Margin):又称增益容限，是指当开关电源的输出随着负载特性的改变而控制环路所对应 频率点的相位为 Odeg 时的增益量。

5.3相位裕度(Phase Margin):又称相位容限，是指当开关电源的输出随着负载特性的改变而控制环路的增 益量下降到0dB时所对应频率点的相位。

(实际是衰减)。

5.4穿越频率(Crossover Frequency ):又称频带宽度，是指在频率 -增益曲线上，增益为零时所对应的频率值。

6.环路稳定性评价方法 6.1环路稳定性评价指标衡量开关电源稳定性的指标是相位裕度和增益裕度。

同时穿越频率，也应作为一个参考指标。

(1) 相位裕度是指：增益降到 0dB 时所对应的相位。

(2) 增益裕度是指：相位为 0deg 时所对应的增益大小(实际是衰减)。

(3) 穿越频率是指：增益为 0dB 时所对应的频率值。

相位裕度，增益裕度，穿越频率，如图2 (波德图)所示。

J 穿越频率图1波德图注：图1中，相位容限即相位裕度，增益容限即增益裕度。

使用运放构成电压跟随器的稳定性问题本文介绍了使用运放构成电压跟随器的稳定性问题及解决方法。

用运放构成电压跟随器的电路，传统教科书仅是简单的把输出和反相输入端连接起来完事儿(如图一)，而实际电路要复杂的多，稳定性问题不可忽视!本文是在一家日本IC厂家网站上找到的，希望对实际应用有一点帮助。

(电压跟随器，顾名思义，就是输出电压与输入电压是相同的，就是说，电压跟随器的电压放大倍数恒小于且接近1。

)电压跟随器的显著特点就是，输入阻抗高，而输出阻抗低，一般来说，输入阻抗要达到几兆欧姆是很容易做到的。

输出阻抗低，通常可以到几欧姆，甚至更低。

在电路中，电压跟随器一般做缓冲级及隔离级。

因为，电压放大器的输出阻抗一般比较高，通常在几千欧到几十千欧，如果后级的输入阻抗比较小，那么信号就会有相当的部分损耗在前级的输出电阻中。

在这个时候，就需要电压跟随器来从中进行缓冲。

起到承上启下的作用。

应用电压跟随器的另外一个好处就是，提高了输入阻抗，这样，输入电容的容量可以大幅度减小，为应用高品质的电容提供了前提保证。

电压跟随器的另外一个作用就是隔离，在HI-FI电路中，关于负反馈的争议已经很久了，其实，如果真的没有负反馈的作用，相信绝大多数的放大电路是不能很好的工作的。

但是由于引入了大环路负反馈电路，扬声器的反电动势就会通过反馈电路，与输入信号叠加。

造成音质模糊，清晰度下降，所以，有一部分功放的末级采用了无大环路负反馈的电路，试图通过断开负反馈回路来消除大环路负反馈的带来的弊端。

但是，由于放大器的末级的工作电流变化很大，其失真度很难保证。

)Q. 用电压跟随器使运算放大器保持稳定，须注意哪些问题?A：对于采用负反馈的放大电路，如何减少振荡以保持稳定，目前尚无定论。

电压跟随器也不例外。

运算放大器理想的运行状态是输出电压和输入电压为同相，即，当负输入端的印加电压引起输出增大时，运算放大器能够相应地使增加的电压降低。

不过，运算放大器的输入端和输出端的相位总有差异。

信息科学与技术学院模拟CMOS集成电路设计——稳定性与频率补偿学习报告姓名：学号：二零一零年十二月稳定性及频率补偿2010-12-3一、自激振荡产生原因及条件1、自激振荡产生原因及条件考虑图1所示的负反馈系统，其中β为反馈网络的反馈系数，并假定β是一个与频率无关的常数，即反馈网络由纯电阻构成，不产生额外的相移(0βϕ=o )；H (s )为开环增益，则()H s β为环路增益。

所以，该系统输入输出之间的相移主要由基本放大电路产生。

图1 基本负反馈系统 该系统的闭环传输函数(即系统增益)可写为：()()1()Y H s s X H s β=+ 由上式可知，若系统增益分母1()H s j βω==-1，则系统增益趋近于∞，电路可以放大自身的噪声直到产生自激振荡，即：如果1()H j βω=-1，则该电路可以在频率1ω产生自激振荡现象。

则自激振荡条件可表示为：1|()|1H j βω=1()180H j βω∠=-o注意到，在1ω时环绕这个环路的总相移是360o ，因为负反馈本身产生了180o 的相移，这360o 的相移对于振荡是必需的，因为反馈信号必须同相地加到原噪声信号上才能产生振荡。

为使振荡幅值能增大，要求环路增益等于或者大于1。

所以，负反馈系统在1ω产生自激振荡的条件为：(1)在该频率下，围绕环路的相移能大到使负反馈变为正反馈；(2)环路增益足以使信号建立。

2、重要工具波特图判断系统是否稳定的重要工具是波特图。

波特图根据零点和极点的大小表示一个复变函数的幅值和相位的渐进特性。

波特图的画法：(1)幅频曲线中，每经过一个极点P ω(零点Z ω)，曲线斜率以-20dB/dec(+20dB/ dec)变化；(2)相频曲线中，相位在0.1P ω(0.1Z ω)处开始变化，每经过一个极点P ω(零点Z ω)，相位变化-45o (±45o )，相位在10P ω(10Z ω)处变化-90o (±90o )；(3)一般来讲，极点(零点)对相位的影响比对幅频的影响要大一些。

多级运算放大器的频率补偿分析Bo yang 2009-5-3 由于单级运算放大器cascode不能满足低电压的要求，而且短沟道效应和深亚微米CMOS的本征增益下降，所以要使用多级放大，这样就涉及到频率补偿的问题。

大部分的频率补偿拓扑结构都是采用极点分离和零极点抵消技术（使用电容和电阻）。

对于两级运算放大器而言这样的补偿无论是在理论分析还是在实际电路中都是可行的，但是对于多级放大器而言，要考虑的因素很多（电容面积，功耗，压摆率等）。

而且理论的分析不一定都适用于实际的电路。

所以对于多级放大器的频率补偿，这里给出了几种拓扑结构。

由于系统结构，传输函数都很复杂，所以在分析这些拓扑结构之前先给出一些假设条件：1）：假设每一级的增益都远远大于1；2）：假设负载电容和补偿电容都大于寄生集总电容；3）：每一级之间的寄生电容忽略不计。

以上这些假设都是很容易满足，而且在大部分电路中都是满足这些条件条件的。

一single stage对于单级放大器而言，其频率响应比较好，只有一个左半平面得极点，没有零点，所以整个系统是稳定的。

极点位置为：。

其增益带宽积为GBW=gmL/CL.所以可以通过增大跨导，减小输出电容的方式来增大带宽。

实际上它的相位裕度没有90度，是因为存在着寄生的零极点。

二这些寄生的零极点于信号路径上的偏置电流和器件的尺寸有关，所以单位增益带宽也不能无限制的增加，而是等于寄生最小极点或者零点的一半为比较合适的，而且大的偏置电流和小的器件尺寸对于稳定性是必要的二 two stage对于两级的运放，就是采用简单的米勒补偿（SMC）。

其补偿的结构如下所示：对于这种结构的传递函数可以表述如下从传递函数中很容易知道零极点位置。

其中一个右半平面得零点和两个极点。

为了保证系统稳定性，次极点和零点要在比单位增益频率大的地方，这样就要求Cm很大并把主极点推的很低,这样增益带宽积就要减小，要保持同样的速度即单位增益带宽，就要求大的功耗（增加跨导）通常选择次极点在单位增益频率两倍的位置。

运放闭环增益稳定判决条件运放（Operational Amplifier, Op-Amp）是现代电子学中最常用的一种基本电子设备，它在模拟信号处理中具有十分重要的作用。

在使用运放时，往往需要对其增益进行控制，以达到所需的电路功能。

而为了保证电路的稳定性，需要对运放的闭环增益进行稳定判决。

本文将就运放闭环增益稳定判决条件进行详细介绍。

一、运放的基本原理和特性运放是一种高增益放大器，其具有低输入阻抗、高输出阻抗、精确的增益和频率响应等特点。

运放的输出电压为其输入电压的差值的比例，一般用下式表示：$$ V_{O} = A_{OL}(V^{+} - V^{-}) $$$V^{+}$和$V^{-}$分别是运放的正负输入电压，$A_{OL}$是运放的开环增益。

根据这个式子，可以推导出运放的闭环增益：$$ A_{CL} = \frac{V_{O}}{V_{I}} = \frac{A_{OL}}{1+A_{OL}\times \beta} $$$V_{I}$为运放的输入电压，$\beta$为反馈电路的反馈比。

从上述公式可以看出，闭环增益与开环增益之间存在倒数关系，即闭环增益越大，开环增益就越小。

为了实现大的闭环增益，需要使用具有高开环增益的运放。

当运放的闭环增益过大时，信号的回路会引入噪声和干扰，从而影响电路的稳定性和精度。

需要对运放的闭环增益进行稳定判决。

（一）相位裕度法相位裕度法是一种常用的运放的闭环增益稳定判决方法，其主要思想是通过稳定性判据来保证电路的稳定性。

相位裕度是指将开环增益曲线的相位角降低到-180°时，系统增益的余裕度。

当相位裕度大于某一阈值时，系统就是稳定的。

该方法通过检测相位裕度来判断系统的稳定性，从而避免了对具体数值的要求。

在实际应用中，相位裕度法的具体稳定判据如下：（1）稳定性判据1：相位裕度$\Delta \varphi$大于$45^{\circ}$。

该判据适用于较大的增益容许范围内。

运放稳定性第5部分（共15部分）：单电源缓冲器电路的实际设计作者：Tim Green，德州仪器公司本系列的第5部分将着重讨论“实际”应用，我们到目前为止所学会的技巧和经验都将得到应用，帮助我们方便地稳定一个复杂的电路。

我们将设计一个通用单电源缓冲放大器（将2.1V 缓冲至4.1V参考），5V单电源供电使它能够线性地工作，可提供较大的输出电流（>13mA），并在 -40°C 至 +125°C工作温度范围的飘移为0.4V。

虽然可将该电路用于许多应用中，但我们仍将简要介绍一下促使给出这个设计的原因，并解释为何没有现成的电路可用来完成此项工作。

我们这里采用综合技术来开发器件网络，以提供一个证明对许多运放应用都有益的稳定电路。

技术背景：在实际应用中，惠斯通电桥的一个常见应用就是压力测量。

如图 5.1所示，随着所加压力变化，很多这种压力传感器都具有明显的二阶非线性特性。

图5.1 典型实际传感器输出比所加压力图字（上、下）：室温下电桥输出与压力关系、理想传感器、实际传感器；坐标轴字： X轴：压力、Y轴：Vexc=1V时的电桥输出（V/V或Vbridge）除了随所加压力变化而产生的非线性外，许多压力传感器随温度变化在偏移量和范围上也有非线性特性。

用来校正这些误差的一种现代解决方法是在压力传感器中内置电子电路，然后将电子电路与压力传感器作为一个模块，随着温度的变化进行数字校准。

一种适用于此类用途的IC是由德州仪器公司提供的Burr-Brown产品PGA309（如图 5.2所示）。

此输出电压已经过数字校准的传感器，其信号调整IC包含有一个模拟传感器线性化电路，该电路将输出电压的一部分反馈至传感器的电压激励引脚，从而以20:1的改良比例对二阶非线性进行线性化。

因此，V EXC引脚将随传感器所加压力的变化而对其电压进行调整。

此电路的一个局限就是其传感器激励引脚V EXC，在工作温度范围内限制在5mA最大输出电流上。