§1.2.2函数的表示法(一)
我们学习了函数的概念及其三耍素，它们初•指的各是什么呢？复习巩固，推陈出新
一、函数的基本概念及其三要素
1.函数的概念
设A、B是非空数集，如果按照某种确定的对应关系f,使对于集合A屮的任意一个数x,在集合B中都有惟一确定的数f (x)和它对应，那么称f： A T B为从集合A到集合B的一个函数，记作：y=f (x), xwA・
2.函数的三要素是什么？
定义域、值域和对应法则是函数的三要素.
今天我们继续研究函数的表示方法.
二、函数的表示法
初屮函数的三种表示方法有哪些?各有什么优点？
函数的表示方法有三种
1.解析法：用数字表达式表示两个变量之I'可的对应关系.
优点：简明，给出自变量x可求出函数值.
2.图像法：用图像表示两个变量之间的对应关系
优点：直观形象，反映变化趋势.
3.列表法：列出表格来表示两个变量之间的对应关系
优点：不需计算，就可看出函数值.注意：①区间是集合；
练习下列三个实例表示的函数各是运用了什么表示方法?
(1)一枚炮弹发射后，经过26s落到地面击中目
标.炮弹的射高为845m,且炮弹距
• •
地血的高度h(单位：m)随吋间t(单位：s)变
化的规律是：h=130t-5t2. (*) 第一张幻灯片
第二张幻灯片
张幻灯片
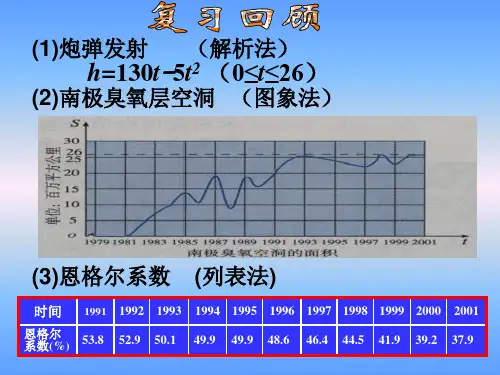
(2)近几十年来，大气层中的臭氧迅
速减少，因而出现了臭氧层空洞问题.图
中的曲线显示了南极上空臭氧层空洞的
面积从1979〜2001年的变化情况.
19791981 1983 1985 1987 1989 1991 1993 1995 1997 1999 2001
南极臭氧层空洞的面枳第三张
幻灯片
3026252015105 .UJ23US
解：这个函数的定义域是数集{1, 2, 3, 4, 5}. 用解析法可将函数y 二f(x)表示为：y=5x,xe
用图象法可将函数y=f(x)表示为
25 20 15 10
小结：函数的图象既可以是连续的曲线，也可以是直线、折线、离散的点.
例1中的函数可用三种表示方法，但并不是每一个函数关系都能用三种表示方法, 我们要学会选择恰当方法表示问题中的惭数关系.
例2下表是某校髙一(1)班三名同学在高一学年度六次数学测试的成绩及 班级平均分表.
第
四张幻灯片 第五张幻灯片
(3)国际上常用恩格尔系数反映一个国家人民生活质量的高低，恩格尔系数 越
低，生活质量越高.表中是“八五”计划以來，我国城镇居民家庭恩格尔系 数随时间(年)变化的情况.
分析：⑴用解析法.(2)用图彖法.(3)用列表法.
典例分析，深化理解
例1某种笔记本的单价是5元，买x(xw {1,2,3,4,5})个笔记本需要y 元.试用 函数的三种方法表示函数y=f(x).
班级平均分
8&2 7&3 85.4 80.3 75.7 82.6
请你对三位同学在高一学年度的数学学习情况作一个分析.
分析：表格是函数的一种表示方法，但对所研究问题的解决，不是很方便，如果将 "成绩”与“测试序号” Z 间的关系用函数图象表示出来，得出4个函数关系如图，那 么就能比较直观地
看到成绩变化的情况.这对我们的分析很有帮助.
100 90
级 平 均 分
赵磊
60
由图我们看到，王伟同学的数学学习成绩始终高于班级平均水平，学习情况比较稳 定而且成绩优秀.张城同学的数学成绩不稳定，总是在班级平均水平上下波动，而且波 动幅度较大.赵磊同学的数学学习成绩低于班级平均水平，但他的成绩曲线呈上升趋势, 表明他的数学成绩在稳步提高.
小结：恰当选择函数的表示方法，巧妙解决实际问题. 练习
1. 如图，把截而半径为25cm 的圆形木头锯成矩形木料，如果矩形的一边长为x,面
解：如图，矩形的对角线就是圆的直径，所以矩形高为：A /502 -X 2 ,Ay=x7502 -X 2
第六张幻灯片
80 70 积为y,把y 表示为x 的函数. 第
七
张
幻灯片
x > 0
注意到实际问题的限制有 ?
?
有Ovxv5O ・
50^-x 2 >0. ■
•I 所求函数为 y=x^502 -X 2 (0<x<50).
2. 下图中哪几个图象与下述三件事分别吻合得最好？请你为剩下的那个图象写出一 件事. (1) 我离开家不久，发现自己把作业本忘在家里了，于是返回家里找到了作业本再上学; (2) 我骑着车一路匀速行驶，只是在途中遇到一次家通堵塞，耽搁了一些时间；
(3) 我出发后，心情轻松，缓缓行进，后来为了赶时间开始加速.
解：(1)与D 图，(2)与A 图，(3)与B 图吻合得最好.剩下与C 图相符的一件事可能 为：我出发后感到时间紧，所以加速前进，后来发现时间还很充裕，于是放慢了速度.
三、分数函数
例3判断下面图象是否为函数？如杲是，则求出定义域、值域和解析式.
解：观察图象知函数定义域为卜1,2]值域为卜1,1]. 当一lWxWO 吋 设 f (x)二kx+b (kHO)
第八张幻灯片
第九张幻灯片
则Oi+方..."1
1 =b[/? = 1
当0<x^2时设f (x) =kx (kxO)
则-l=2k ・・.k二一丄
2 •：f (x)二x+1 ••f(x)=4x
x + l, -1 < x < 0
综上所求：f(x)=J 1
—x, 0 v x 5 2 2
象上面的函数f(x)称为分段数函数.
注意：分段函数是一个分段书写的函数，不是多个函数.
练习
3画出函数y=|x|的图象. 第十张幻灯片
解：由绝对值的概念，我们有
x, x>0, y=s
-x. x<0.
所以,函数y=|x|的图象如图所示. 练习
x+4, x<0,
4.已知函数y= F _2兀,o v x W 4,求f{f[f(5)J)的值.
-x+2.兀>4. 第卜一张幻灯
解：・・・5>4,・・・f(5) = —5+2=—3. ・・・一3v0,
・・・ f [f ⑸]=f (-3)= -3+4二1.・・・ 0<1 <4, ・•・f{flf(5)]}=f( 1)=12-2x 1=-1,B卩f{f[f(5)]}= -1.
例4某市“招手即停”公共汽车的票价按下列规则制定：
(1) 5公里以内(含5公里)，票价2元；
(2) 5公里以上，每增加5公里，票价增加1元(不足5公里的按5公里计算). 如果某条线
路的总里程为20公里，请根据题意，写出票价与里程Z 间的函数解 析式，并画出函数图象.
解：设票价为y,里程为x,由题意可知，自变量x 的取值范围是(0,20]. 由“招手即停”公共汽车票价的制定规则， 可得到以下函数解析式：
2, 0 < x < 5, _ 3, 5 < x < 10,
y_
|4, 10<x<15, 5, 15 < x < 20.
根据这个函数解析式，诃画出函数图象，如图. 回顾反思，提炼升华
一、从知识技能上
解析法
1. 函数的表示法图像法
列表法
注意：恰当选择
2. 分段函数①图象、分段函数.
② 定义域，分段x 范围的并集.
③ 值域，分段y 范圉的并集. 注意：分段函数是一个函数.
二、从思想方法上 数形结合
演练平台，巩固提高
1. 第27页习题1.2A 组第7、8、9题.第49页B 组7题.
-X 2 + 2x, x > 0,
2.
己知函数 f (x)= 1, x = 0,
—
1, x < 0.
⑴求 f (-l),f[f(-l)],f{ fff(-i)]!的值； ⑵画出函数的图彖.
3. ______________________________________________________________ 若定义运算aOb=b a ~h :则函数f (x)=xO (2-x)的值域是 ____________________________________
a 、 a <b,
第十三张幻灯
第27页习题1.2A组第7题
(I)
8.例如，y二巴(x>0),/=2x+— (x>0),P2jd2+20 .
2
9.x二上定义域[0, 回1],值域[0, h],
nd-4v
第49页B组7题：设某人月工资、薪金所得为x元，应纳此项税款为y元, 0, 0<x< 800,
(x-800)x5%, 80() <x< 1300,
Hll
则y=<
25 + U-l300)xlO%, 1300 <x< 2800,
175 + (x - 2800) x 15%, 2800 <x< 5800.
由于某人一月份应纳税款为26. 78元，
故必有130(KxW2800,从而26. 78二25+(x-1300)x 10%,解得x=1317.8 元所以，某人一月份的工资、薪金为1317.8元.
2. (l)f(-l)=0；f[f(-l)] =f(O)=l;f{f [f(-1)] }=f(l)= -12+2X 1 = 1.
⑵函数图象如图所示
3.(—g,l]・。
