4.8 图形的位似 第二课时导学案

图形的位似2导学案班级：九年级学生姓名：使用时间：10月27日【学习目标】1、能熟练准确地利用图形的位似在直角坐标系中将一个图形放大或缩小；2、经历探究平面直角坐标系中，以O为位似中心的多边形的坐标变化与相似比之间关系的过程，领会所学知识，归纳作图步骤，总结规律，并较熟练地进行应用。

3、通过实例进一步理解位似图形及相关概念和性质。

【重点】通过探究得到平面直角坐标系中多边形坐标变化与其位似图形的关系，并能应用该结论将一个多边形放大或缩小。

【难点】比较在坐标系中放大或缩小后的图形与原图形的坐标与相似比，总结规律。

【学法指导】合作交流，自主探究【课时安排】 1 课时总第42课时相关知识回顾：1、什么是位似图形？2、如何判断两个图形是否位似？3、怎样求两个位似图形的相似比？4、如何将画在纸上的一个图片放大，使放大前后对应线段的比为1：2？你有哪些方法？预习要求：通过预习初步了解本节知识点，并根据个人能力初步完善探究案。

学科组长组内检查组内各对子预习完成情况。

一、情景引入：二、PPT出示教学目标。

三、“先学后教”——探索位似图形的坐标变化规律活动内容：在直角坐标系中，△OAB三个顶点的坐标分别为O（0,0），A（3,0），B（2,3）. 按要求完成下列问题：（小组内互助探索完成，比一比哪个小组完成最快、最准确）（1）将点O，A，B的横、纵坐标都乘以2，得到三个点O′，A′，B′，请你在坐标系中找到这三个点。

（2）以这三个点为顶点的三角形与△OAB位似吗？为什么？（3）如果位似，指出位似中心和相似比。

（4）如果将点O，A，B的横、纵坐标都乘以-2呢？思考：观察所作图形，你有什么发现？预习案——课前自主学习探究案——课中合作探究掌握一个解题方法，比做一百道题更重要。

学习不怕根基浅，只要迈步总不迟。

做一做：（小组合作操作发现规律）（1）在直角坐标系中，四边形ABCD的顶点坐标分别为A（4,2），B（8,6），C（6,10），D（-2,6）.将点O，A，B，C的横、纵坐标都乘21，得到四个点，以这四个点为顶点的四边形与四边形ABCD位似吗？如果位似，指出位似中心和相似比.（2）如果将点A，B，C,D的横、纵坐标都乘-21呢？思考：通过前面的探究，你发现了什么？（根据上述问题的解决，试归纳位位似图形的坐标变化规律）结论：在平面直角坐标系中，将一个多边形每个顶点的横、纵坐标都乘以同一个数k（k ≠0），所对应的图形与原图形，位似中心是，它们的相似比为.四、当堂检测：如图，在直角坐标系中，四边形OABC的顶点坐标分别是O（0,0），A（3,0），B（4,4），C（-2,3）.画出四边形OABC以O为位似中心的位似图形，使它与四边形OABC的相似比是2:1.五、小结：（小组内总结组内成员完成了本节的几个学习目标）六、作业：A组：B组:我的收获（学生）/课后反思（教师）人贵有志，学贵有恒。

图形的位似〔第2课时〕一、问题引入：在直角坐标系中，△OAB 三个顶点的坐标分别为O 〔0,0〕，A 〔3,0〕，B 〔2,3〕.按要求完成以下问题：〔1〕将点O ，A ，B 的横、纵坐标都乘以2，得到三个点O ′，A ′，B ′，请你在坐标系中找到这三个点. 〔2〕以这三个点为顶点的三角形与△OAB 位似吗？为什么？〔3〕如果位似，指出位似中心和相似比.〔4〕如果将点O ，A ，B 的横、纵坐标都乘以-2呢？总结：在直角坐标系中，将一个多边形每个顶点的横、纵坐标都乘以同一个数k 〔k ≠0〕，所对应的图形与原图形位似，位似中心是坐标原点，它们的相似比为∣k ∣.二、根底训练：在直角坐标系中，四边形OABC 的顶点坐标分别为O 〔0,0〕，A 〔2,4〕，B 〔-2,5〕，C 〔-4,0〕.将点O ，A ，B ，C 的横、纵坐标都乘21，得到四个点，以这四个点为顶点的四边形与四边形OABC 位似吗？如果位似，指出位似中心和相似比.三、例题展示：在直角坐标系中，四边形OABC 的顶点坐标分别为O 〔0,0〕，A 〔6,0〕，B 〔3,6〕，C 〔-3,3〕.四边形O ′A ′B ′C ′与四边形OABC 是以原点O 为位似中心的位似四边形，且相似比是3:2，请写出四边形O ′A ′B ′C ′各个顶点的坐标.四、课堂检测：如图，在直角坐标系中，四边形OABC 的顶点坐标分别是O 〔0,0〕，A 〔3,0〕，B 〔4,4〕，C 〔-2,3〕.画出四边形OABC 以O 为位似中心的位似图形，使它与四边形OABC 的相似比是2:1.菱形的性质与判定〔第3课时〕一、问题引入1、菱形的定义：叫菱形.2、菱形的性质：〔1〕具有平行四边形的所有性质〔边、角、对角线、对称性〕.〔2〕特殊性质：①边：菱形；②对角线：菱形，③对称性：菱形是图形(对称轴是：)；④面积：菱形的面积等于。

3、菱形的判别：〔1〕边：①一组相等的是菱形〔定义〕；②相等的是菱形；〔2〕对角线：①对角线的平行四边形是菱形；②对角线的四边形是菱形。

27§4.8图形的位似 (二【学习目标】1、掌握位似图形在直角坐标系下的点的坐标的变化规律;2、能利用直角坐标系下位似图形对应点坐标变化的规律来解决问题; 【学习重点】平面直角坐标系下的位似变换;【学习难点】把一个图形按一定大小比例放大或缩小后,点的坐标变化的规律; 【学习过程】(一预习案:1. 观察下列相似图形,归纳其特点归纳:(1两个图形是 ; (2每组相交于一点; (3 互相平行。

具有上述特点的图形是位似图形,对应点连线的交点是位似中心。

点拨:相似图形不一定是位似图形,但位似图形一定是相似图形; 2. 位似图形的性质(1位似图形具有图形的一切性质;(2位似图形任意一对对应点到位似中心的距离之比都位似比;3. 图形变换我们学习过的图形变换包括: ,轴对称,旋转和 ;4.△ ABC 三个顶点坐标分别为 A(2,3, B(2,1, C(6,2(1将△ ABC 向左平移三个单位得到△ A 1B 1C 1,写出 A 1、 B 1、 C 1三点的坐标;(2写出△ ABC 关于 x 轴对称的△ A 2B 2C 2三个顶点 A 2、 B 2、 C 2的坐标;(3将△ ABC 绕点 O 旋转 180°得到△ A 3B 3C 3,写出 A 3、 B 3、 C 3三点的坐标.(二探究案:1. 在平面直角坐标系中有两点 A (6, 3 , B (6, 0 ,以原点 O 为位似中心,相似比为1:3,把线段 AB 缩小 .(2在方法二中, A ’’的坐标是, B ’’的坐标是 ,对应点坐标之比是 2. 如图,△ ABC 三个顶点坐标分别为 A(2,3, B(2,1, C(6,2.以点o 为位似中心, 相似比为2, 将△ ABC 放大, 观察对应顶点坐标的变化, 你有什么发现?位似变换后 A , B , C 的对应点为A ' ( , ,B ' ( , ,C ' ( , ; A"( , , B" ( , , C" ( , .归纳:在平面直角坐标系中,如果位似变换是以原点为位似中心 ,相似比为 k ,那么位似图形对应点的坐标的比等于 ; (三训练案:1. △ ABO 的顶点坐标分别为 A(-1,4, B(3,2, O(0,0, 试画出将△ ABO 放大为△EFO , 使△ EFO 与△ABO的相似比为 2.5∶ 1的图形,写出点 E 和点 F 的坐标.2. 如图,△ AOB 缩小后得到△ COD ,观察变化前后的三角形顶点, 坐标发生了什么变化,并求出其相似比和面积比.3. 如图,原点 O 是△ ABC 和△ A ′ B ′ C ′的位似中心,点 A (1, 0 与点A ′ (-2, 0 是对应点,△ ABC 的面积是 23,则△ A ′ B ′ C ′的面积是 ________________.。

第2课时坐标中的位似关系1.使学生理解掌握位似图形在平面直角坐标系上的应用，即会根据相似比，求位似图形顶点，以及根据位似图形对应点坐标，求位似图形的相似比和在平面直角坐标系上作出位似图形.2.让学生在应用有关知识解决问题的过程中，提高应用意识，体验数形结合的思想方法在解题中的运用.阅读教材P115-117，自学“做一做”与“例2”，掌握以原点为位似中心的两个位似图形对应顶点的坐标规律. 自学反馈学生独立完成后集体订正①如图，在平面直角坐标系中，有两点A(6，3)、B(6，0)，以原点O为位似中心，相似比为13，把线段AB缩小，观察对应点之间坐标的变化，你有什么发现？②在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k,那么位似图形对应点坐标的比为.③△ABC和△A1B1C1关于原点位似且点A(-3，4)，它的对应点A1(6，-８)，则△ABC和△A1B1C1的相似比是.④已知△ABC三顶点的坐标分别为A(1,2),B(1,0),C(3,3),以原点O为位似中心，相似比为2，把△ABC放大得到其位似图形△A1B1C1，则△A1B1C1各顶点的坐标分别为A1,B1,C1.注意分两种情况.活动1 小组讨论例1将图形中的△ABC作下列移动，画出相应的图形，指出三个顶点的坐标所发生的变化.①向上平移4个单位；②关于y轴成轴对称；③以点A为位似中心，放大到2倍.解:①平移后得△A1B1C1，横坐标不变，纵坐标都加4；②△ABC关于y轴成轴对称的图形为△A2B2C2，纵坐标不变，横坐标为对应点横坐标的相反数；③放大后得△AB3C3，A的坐标不变，B3在B的基础上纵坐标不变，横坐标加AB的长，C3的横坐标在C的横坐标的基础上加AB的长，纵坐标在C的纵坐标系的基础上加BC的长.考虑图形在平面直角坐标系中作何种变换，弄清点的坐标的变化情况；作位似变换时，求出顶点坐标即可.活动2 跟踪训练(独立完成后展示学习成果)1.某个图形上各点的横、纵坐标都变成原来的12，连接各点所得图形与原图形相比( )A142.如果一个直角三角形的两条边长分别是6和８，另一个与它相似的直角三角形边长分别是3和4及x，那么x的值( )活动1 小组讨论例2 如图所示的△ABC，以A点为位似中心，放大为原来的2倍，画出一个相应的图形，并写出相应的点的坐标.解:根据题意，图中的△AB1C1就是满足题意的三角形，其中A点的坐标不变，仍是(-3，-1)，B1、C1的坐标分别为(3，-3)，(1，3).解决本题的关键就是要作出正确的图形，否则求出的点的坐标就会发生错误.活动2 跟踪训练(独立完成后展示学习成果)在平面直角坐标系中，将坐标为(0，0)、(2，4)、(2，0)、(4，4)、(6，0)的点用线段顺次连结起来形成一个图案.①将这五个点的纵坐标不变，横坐标变为原来的13，求上述点的坐标，将所得的五个点用线段顺次连接起来，所得图案与原图案相比有什么变化？②横坐标不变，纵坐标分别减去3呢？③横坐标都加上3，纵坐标不变呢？④横、纵坐标都乘以-1呢？⑤横、纵坐标分别变成原来的2倍呢？面积如何变化？活动3 课堂小结1.本节学习的数学知识:以原点为位似中心，位似图形对应点之间的坐标的关系.2.本节学习的数学方法:运用数形结合的方法解题.教学至此，敬请使用《名校课堂》相应课时部分.【预习导学】自学反馈①略②k或-k③1 2④A1（2,4）或（-2,-4）、B2（2,0）或（-2,0）、C1（6,6）或（-6，-6）【合作探究1】活动2 跟踪训练【合作探究2】活动2 跟踪训练①横向缩小1 3②向下平移3个单位长度③向右平移3个单位长度④关于原点作中心对称变换⑤以原点为位似中心作位似变换，相似比为2，面积扩大4倍。

2021秋北师版九上数学4.8.2位似图形与坐标导学案学习目标：1、 了解平面直角坐标系下位似变换图形坐标的特点.2、 能够熟练准确地利用坐标变化将一个图形放大或缩小.学习策略1. 教师应充分立足于学生实际情况，予以适当引导，在恰当的时候给予提示或引起思维碰撞，同时借助多媒体课件进行演示，学生将会很快进入学习状态..2. 使学生进一步理解位似的相关概念，熟练掌握利用直角坐标系将一个图形按比例放大或缩小，进而能初步归纳出规律，形成有关技能，发展思维能力。

学习过程一.复习回顾1、把一个图形变成另一个图形，并保持图形形状不变的几何变换叫做_________.2、如果两个图形不仅相似，而且每组对应点所在的直线__________，那么这样的几何变换叫做___________，这样的两个图形叫做___________．3、图形在平面直角坐标系中作平移变换时坐标的变化规律是(h>0)：向左平移h 个单位→),(b a (_ _,b)，向右平移h 个单位→),(b a (____,b)；向上平移h 个单位,(),(a b a →___)，向下平移h 个单位,(),(a b a → __).二.学习新课阅读课本115-117页，回答下列问题：1、在平面直角坐标系中，如果位似变换是以原点O 为位似中心，相似比为K （K ＞0），原图形上点的坐标为（x,y ），那么同向位似图形对应点的坐标为___________（K ＞0）.2、在平面直角坐标系中，在作),(),(by ax y x →变换时，当0≠=b a 时为相似变换；当b a ≠时便不是相似变换，我们称之为___________ ．3、在问题1中若K ＜0，则与K ＞0时的变换结果有什么不同？4．如图，△ ABC 三个顶点坐标分别为A(2,3)，B(2,1)，C(6,2).（1）将△ ABC 向左平移三个单位得到△ A 1B 1C 1，写出三点的坐标；（2）写出△ ABC 关于x 轴对称的△ A 2B 2C 2三个顶点A 2、B 2、C 2的坐标；（3）将△ ABC 绕点O 旋转180°得到△ A 3B 3C 3，写出三点的坐标．5、在平面直角坐标系中有两点A （6，3），B （6，0），以原点为位似中心，相似比为1:2，把线段AB 缩小 方法一：方法二：探究： （1）在方法一中，'A的坐标是 ，'B 的坐标是 ，对应点坐标之比是 ；（2）在方法二中，''A 的坐标是 ，''B 的坐标是 ，对应点坐标之比是三.尝试应用1.如图，ABC ∆三个顶点坐标分别为()2,3A ()2,1B ()3,1C ，以点O 为位似中心，相似比为２，将ABC ∆放大，观察对应顶点坐标的变化，你有什么发现？归纳：在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k ，那么位似图形对应点的坐标的比等于 ；2.如图，在平面直角坐标系中，四边形ABCD 的坐标分别为A （-6,6），B （-8,2），C(-4,0)D （-2,4）画出一个以四.自我总结1.位似图形与位似中心有两种情况：（1）位似图形在位似中心两侧；（2）位似图形在位似中心同侧.若题中未指明位置关系，应该分两种情况讨论，2. 画以原点为位似中心的位似图形的方法：将一个多边形各点的横坐标与纵坐标都乘±k（或除以±k），可得新多边形各顶点的坐标，描出这些点并顺次连接这些点即可.五.达标测试一、选择题1．如图，以点O为位似中心，将△ABC缩小后得到△A′B′C′，已知OB=3OB′，则△A′B′C′与△ABC的面积比为（）A．1：3 B．1：4 C．1：5 D．1：92．如图，在平面直角坐标系中，已知点A（﹣3，6），B（﹣9，﹣3），以原点O为位似中心，相似比为，把△ABO 缩小，则点A的对应点A′的坐标是（）A．（﹣1，2） B．（﹣9，18）C．（﹣9，18）或（9，﹣18）D．（﹣1，2）或（1，﹣2）3．如图，在平面直角坐标中，正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形，且相似比为，点A，B，E在x轴上，若正方形BEFG的边长为6，则C点坐标为（）A．（3，2）B．（3，1）C．（2，2）D．（4，2）二、填空题：4．如图，在平面直角坐标系中，已知A（1，0），D（3，0），△ABC与△DEF位似，原点O是位似中心．若AB=1.5，则DE= ．5．如图，直线y=x+1与x轴交于点A，与y轴交于点B，△BOC与△B′O′C′是以点A为位似中心的位似图形，且相似比为1：3，则点B的对应点B′的坐标为．6．如图，O点是△ABC与△D1E1F1的位似中心，△ABC的周长为1．若D1、E1、F1分别是线段OA、OB、OC的中点，则△D1E1F1的周长为；若OD2=OA、OE2=OB、OF2=OC，则△D2E2F2的周长为；…若OD n=OA、OE n=OB、OF n=OC，则△D n E n F n的周长为．（用正整数n表示）三、解答题：7.已知：如图△ABC三个顶点的坐标分别为A（0，﹣3）、B（3，﹣2）、C（2，﹣4），正方形网格中，每个小正方形的边长是1个单位长度．（1）画出△ABC向上平移6个单位得到的△A1B1C1；（2）以点C为位似中心，在网格中画出△A2B2C2，使△A2B2C2与△ABC位似，且△A2B2C2与△ABC的位似比为2：1，并直接写出点A2的坐标．8．如图，以原点O为位似中心，把△OAB放大后得到△OCD，求△OAB与△OCD的相似比．达标测试答案：一．选择题1． D.2. D．3. A．二．填空题4. 4.5．5.（﹣8，﹣3）或（4，3）．6. ．三．解析题7.解：（1）如图所示：△A1B1C1，即为所求；（2）如图所示：△A2B2C2，即为所求，A2坐标（﹣2，﹣2）．8. 解：∵点B的坐标是（4，0），点D的坐标是（6，0），∴OB=4，OD=6，∴==，∵△OAB与△OCD关于点O位似，∴△OAB与△OCD的相似比．。

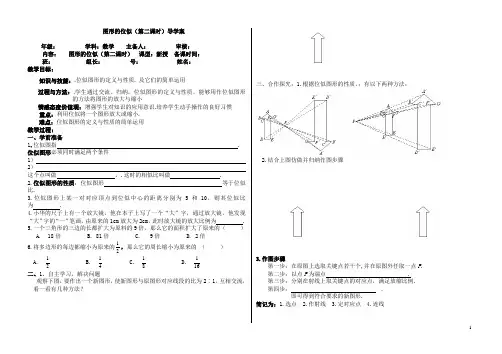
图形的位似（第二课时）导学案年级： 学科：数学 主备人： 审核： 内容： 图形的位似（第二课时） 课型：新授 备课时间： 班： 组长： 号： 姓名： 教学目标：知识与技能：.位似图形的定义与性质. 及它们的简单运用过程与方法：.学生通过交流、归纳，位似图形的定义与性质，能够用作位似图形的方法将图形的放大与缩小情感态度价值观：增强学生对知识的应用意识.培养学生动手操作的良好习惯 重点：利用位似将一个图形放大或缩小. .难点：位似图形的定义与性质的简单运用 教学过程：. 一、学前准备1.位似图指 . 位似图形必须同时满足两个条件1） 2） 这个点叫做 ，.这时的相似比叫做 .2.位似图形的性质：位似图形 等于位似比.3.位似图形上某一对对应顶点到位似中心的距离分别为5和10，则其位似比为 .4.小华的尺子上有一个放大镜，他在本子上写了一个“大”字，通过放大镜，他发现“大”字的“一”笔画，由原来的1cm 放大为2cm ，此时放大镜的放大比例为 .5.一个三角形的三边的长都扩大为原料的9倍，那么它的面积扩大了原来的（ ） A. 18倍 B. 81倍 C. 9倍 D. 2倍6.将多边形的每边都缩小为原来的21，那么它的周长缩小为原来的 （ ）A. 21B. 41C. 81D. 161二、1、自主学习，解决问题 观察下图，要作出一个新图形，使新图形与原图形对应线段的比为2∶1，互相交流，看一看有几种方法？三、合作探究：1.根据位似图形的性质，；有以下两种方法：2.结合上图仿做并归纳作图步骤3.作图步骤第一步：在原图上选取关键点若干个,并在原图外任取一点P . 第二步：以点P 为端点 . 第三步：分别在射线上取关键点的对应点，满足放缩比例. 第四步： .即可得到符合要求的新图形.简记为：1.选点 2.作射线 3.定对应点 4.连线4、课堂练习：1、判断正误：（1）分别在△ABC的边AB、AC上取点D、E,使DE∥BC,那么△ADE是△ABC缩小后的图形. （）（2）分别在△ABC的边AB、AC的延长线上取点D、E,使DE∥BC,那么△ADE是△ABC放大后的图形.（）（3）分别在△ABC的边AB、AC的反向延长线上取点D、E,使DE∥BC,那么△ADE是△ABC放大后的图形.（）四、当堂测试1.七边形ABCDEFG与七边形A′B′C′D′E′F′G′是位似图形，它们的面积比为4:9,已知位似中心O到A的距离为6，则O到A′的距离为（）A. 13.5B. 12C. 18D. 92.已知如图1，ΔABC，在ΔABC外任取一点O,在射线AO、BO、CO上分别取点D、E、F，使DO=2OA，EO=2OB，FO=2OC ,连接三点D、E、F，得到ΔDEF,则下列说法正确的是（）①. ΔABC与ΔDEF是位似图形②. ΔABC与ΔDEF是相似图形③．ΔABC与ΔDEF的周长比为2：1 ④. ΔABC与ΔDEF的面积比为1：4A. 1个B. 2 个C. 3个D. 4个图1 图23.ΔABO的顶点坐标分别为A (－3,3),B (3,3), O (0,0),试将ΔABO放大为ΔEFO,使ΔEFO与ΔABO的位似比为2：1，则E点的坐标为，点F的坐标为 .4.如图2，已知矩形ABCD与矩形A′B′C′D′是位似图形，53'=PBPB，求矩形ABCD与矩形A′B′C′D′的面积比5.已知ΔABC，作一个ΔDEF，使新图形与原图形的对应线的比为1 ：2五：学习体会：（1）本节课我的收获是：（2）本节课我的的疑惑是：（3）你对老师关于本课的教学有什么建议六、应用与拓展：1、教材159、160页练习2、如图，在∆ABC中，AB=8cm，BC=16cm，点P从点A开始沿边AB向点B以2cm/s的速度移动，点Q从点B开始沿边BC向点C以4cm/s的速度移动，如果点P、Q分别从点A、B同时出发，经几秒钟相似？试说明理由。

北师大版九年级上册8图形的位似第四章：图形的位似课时二教学设计一、教学目标1.了解图形的位似概念及其性质。

2.学习解决实际问题中的位似应用，如计算建筑物高度。

3.学习通过绘制图形进行位似变换。

4.培养学生的分析、推理、解决问题的能力。

二、教学重点1.图形的位似概念及其性质。

2.通过绘制图形进行位似变换。

三、教学难点1.将位似的性质应用于实际问题。

2.提高图形绘制技巧，达到熟练操作的程度。

四、教学过程1. 导入新知通过引导学生观察一张照片，提出如下问题：1.你觉得这幢楼房高度有多少米？2.你是如何得到上述答案的？引导学生分析不同楼层间的比例关系，通过图形的相似性质，推算出整幢楼房的高度。

2. 学习新知1.讲解图形的位似概念及其性质。

通过比较几个位似图形的相似性质，引导学生发现它们之间的关系。

2.分组练习。

每组给出一些相似图形，要求学生在纸上画出它们的位似形态，并标注出比例尺，交给教师检查。

教师可以根据学生的表现，及时统计出各组完成情况，给予组内的集体表扬。

3.解决实际问题中的位似应用。

举例说明如何利用位似性质来计算建筑物的高度等实际问题。

3. 知识拓展引导学生寻找身边的例子，分析其中的位似关系及其应用。

4. 小结与归纳通过对位似概念的讲解和实际应用的解决，总结出位似的性质和特点。

五、教学评估将几组相似图形分发给学生，要求他们根据比例尺求出各图形之间的比例，评估学生对图形位似概念及其性质的掌握情况。

同时，让学生通过绘图的形式，进行位似变换，评估学生对位似技能的熟练程度。

六、课后作业1.练习册P28，1b；2.结合身边的例子，总结位似性质和应用，写出一份小结。

3.提前预习下一节课相关内容。

七、板书设计图形的位似定义：在同一平面内，如果两个图形形状相似并且对应边长度的比相等，则这两个图形相似。

性质：1.相似图形的所有对应角相等；2.相似图形的每一对对应边的比例相等；3.相似图形的对应线段长度的比等于相应对应边长的比。