六年级数学培优测试(五)

人教版数学六年级上册第五单元班级________ 姓名______ 分数_______一、填空题。

（25分）1．大圆的半径是小圆半径的3倍,大圆的周长是小圆周长的（）倍,大圆面积是小圆面积的（）倍。

2．一个圆的周长是12.56cm,这个圆的直径是（）cm,这个圆的面积是（）cm2。

3．小芳用尺子量得圆形桌面的直径是1.2m,这个圆形桌面的周长是（）m。

4．一个圆的周长、直径、半径相加的和是27.84厘米,这个圆的面积是（）平方厘米。

5．用圆规画一个直径为10cm的圆,圆规两脚间的距离是（）cm。

6．一根铁丝刚好可以围成一个边长为3.14分米的正方形,用这根铁丝可以围成一个周长是（）分米的圆,这个圆形的面积是（）平方分米。

7．在边长是4dm的正方形纸上剪一个最大的圆,这个圆的面积是（）dm2。

8．君君画了两个同心圆,半径分别是3厘米和4厘米,这两个圆的面积相差（）。

9．一个钟表分针长10厘米,时针长8厘米,从2时走到3时,分针所扫过的面积是（）平方厘米,分针尖端走过的周长是（）厘米；从3时到6时,时针扫过的面积是（）平方厘米。

10．在长8分米、宽6分米的长方形中画一个最大的圆,圆的直径是（）分米。

二、选择题。

（12分）1．小明买了一个台玩具越野车,前轮直径是后轮的一半,后轮滚动6圈,前轮要滚动（）圈。

A．3 B．12 C．92．一个圆的半径由2cm增加到3cm,这个圆的面积增加了（）cm2。

A．5πB．πC．13．小圆的直径是8cm,大圆的半径是5cm,小圆的面积是大圆面积的（）。

A．45B．54C．1625D．19104．如图,两个图形中的阴影部分周长和面积大小关系是（）。

A．周长和面积都相等B．周长不相等,面积相等C．面积不相等,周长相等5．圆是平面上的（）。

A．直线图形B．曲线图形C．无法确定6．以下图形周长相等,则（）面积最大。

A．长方形B．正方形C．圆三、判断题。

（10分）1．从大圆里剪掉一个小圆就得到一个圆环。

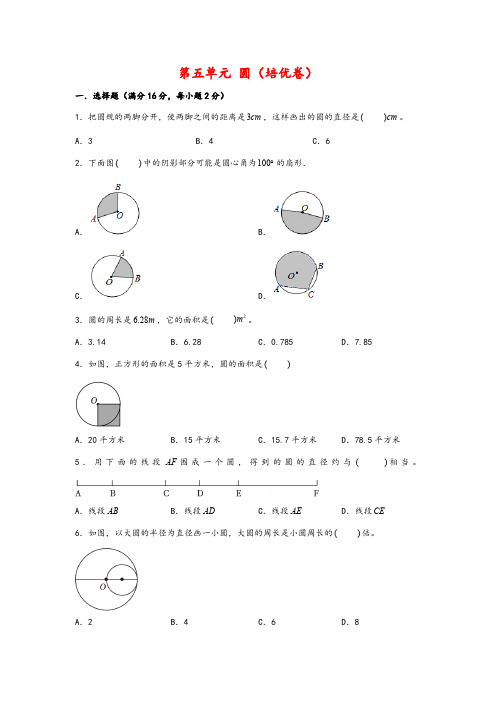
第五单元 圆（培优卷）一．选择题（满分16分，每小题2分）1．把圆规的两脚分开，使两脚之间的距离是，这样画出的圆的直径是 。

A ．3B ．4C ．62．下面图 中的阴影部分可能是圆心角为的扇形．A ．B．C ．D ．3．圆的周长是，它的面积是 。

A．3.14B ．6.28C ．0.785D ．7.854．如图，正方形的面积是5平方米，圆的面积是 A ．20平方米B ．15平方米C ．15.7平方米D ．78.5平方米5．用下面的线段围成一个圆，得到的圆的直径约与 相当。

A ．线段B ．线段C ．线段D ．线段6．如图，以大圆的半径为直径画一小圆，大圆的周长是小圆周长的 倍。

A ．2B ．4C ．6D ．83cm ()cm ()100 6.28m (2)m ()AF ()AB AD AE CE()A．长方形的宽等于圆的半径B．长方形的面积等于圆的面积C．如果长方形的长是6.28厘米，那么圆的周长是15．圆的直径扩大到原来的6倍，它的周长扩大到原来的倍。

4cm2cm16．一张长、宽的长方形纸，如果剪一个最大的圆，圆的面积是六．解答题（满分48分，每小题6分）23．（6分）下图是一个圆形花坛的平面图，现在设计师要在圆形花坛的周围修一条宽是1厘米的环形小路，请你帮他画出这条小路，并用阴影表示出来。

并计算出环形小路的面积。

24．（6分）如图是利用两面墙作边，用栅栏围成的一个扇形羊圈，羊圈的直径是8米。

这个羊圈的面积是多少平方米？25．（6分）水滴滴入水中，平静的水面会产生近似圆形的波纹，假设波纹以每秒1米的速度向四周扩散，隔一秒会产生一个新的波纹并且以相同的速度向四周扩散，一滴水滴入水中3秒后，产生的第一个波纹比第二个波纹的面积大多少平方米？26．（6分）一个圆形餐桌面的直径是1.2米。

（1）如果一个人约需要宽的位置就餐，这张餐桌最多能坐多少人？（2）如果在这张餐桌的中央放一个直径是的圆形转盘，剩下的桌面的面积是多少平方米？27．（6分）压路机的前轮直径是1.2米，宽2米，这种压路机前轮滚动一周可以前进多少米？压过的面积是多少平方米？28．（6分）一个圆形花坛的周长是62.8米，为了扩大种植的面积，将它的半径增加了2米后，它的面积是多少？29．（6分）学校操场上的环形跑道如图所示，求出跑道的全长和围成的面积．（单位：米）30．（6分）在一个直径是的圆形花坛周围铺设一条宽的水泥路，这条水泥路的面积0.4m 1m 8m 1m是多少？参考答案一．选择题（满分16分，每小题2分）1．把圆规的两脚分开，使两脚之间的距离是，这样画出的圆的直径是 。

北师大版六年级上册数学第五单元数据处理培优测试卷一、选择题1．为了清楚地比较韶关和北京两城市2018年7月平均气温的变化情况，最好选用（）统计图。

A．单式折线B．复式折线C．复式条形D．扇形2．要知道深圳已接种新冠疫苗的人中18岁以下、18—59岁、60岁及以上的分别占接种总人数的百分比，选用（）统计图；要清楚地对比神舟十二号上三名航天员在火箭升空期间每分脉搏次数的变化情况，选用（）统计图。

A．条形；扇形B．折线；扇形C．扇形；条形D．扇形；折线3．菜园里种了三种菜（如下图），用条形统计图表示各种菜的占地面积应该是（）。

A．B．C．D．4．六年三班有48名同学，一次数学测试的成绩统计如下，下面统计图（）能表示出这个结果。

A．B．C．D．5．某校开展以“了解传统习俗，弘扬民族文化”为主题的实践活动。

实践小组就“是否知道端午节的由来”对部分学生进行了调查，调查结果如图所示，其中不知道的学生有8人。

下列说法不正确的是（）。

A．被调查的学生共有50人D．全校“知道”的人数约占全校总人数的64%6．如图所示，是育才学校六年级1班最喜欢上的课的调查结果的扇形统计图，则阴影部分表示（）。

A．最喜欢语文课的有25人B．不喜欢语文课的有25人C．最喜欢语文课的人数占全校学生数的25%D．不喜欢语文课的人数占全校学生数的25%7．六（1）班美术兴趣小组的人数是全班人数的27.1%，下面是制作统计图是画的4个草图，其中图（）能比较正确地表示这个百分比。

A．B．C．D．8．一件毛衣各种材料占总质量的情况为：7%棉、25%涤纶、68%羊毛．下面哪个图能正确地表示这个信息?( )A．B．C．D．二、填空题9．反映甲、乙两个商场2020年四个季度销售的变化情况，用( )统计图比较好。

10．某社区对6月之前的社区内居民接种新冠疫苗的情况进行了统计，统计情况如下图，已知接种1针的人数有1900人，则该社区一共有( )人，接种3针的有( )人。

人教版六年级数学下册第四、五单元培优测试卷一、填空。

(每空1分，共25分)1.小红用水和蜂蜜为一家人调制了四杯蜂蜜水，蜂蜜与水的配比如下：第一杯第二杯第三杯第四杯蜂蜜50mL 40mL 60mL 50mL水250mL 240mL 300mL 200mL小红把同样甜的两杯蜂蜜水给爸爸和妈妈，爸爸和妈妈喝的是第()杯和第()杯，把最甜的一杯蜂蜜水给弟弟，弟弟喝的是第()杯。

2.25∶8的比值是()，如果比的后项加上72，要使比值不变，前项要变成()。

3.已知一个比例是由两个比值是4的比组成的，又知道比例的两个外项分别是1.2和5，这个比例是()。

4.如果7a＝8b，那么a∶b＝()∶()。

5.如果2m ＝mn＝15，那么m＝()，n＝()。

6.如果x＝6y，那么x和y成()比例；一部电视剧的总集数一定，每天播放的集数和播放的天数成()比例。

7.二十四节气中的“夏至”是一年中白昼最长、黑夜最短的一天。

2023年6月21日是“夏至”，这一天宁波地区白昼时长的15等于黑夜时长的725，那么白昼和黑夜的时长比是()。

8.一幅地图的比例尺是，把它改写成数值比例尺是()。

宁波到杭州的实际距离大约是180km，那么从这幅地图上量得宁波到杭州的距离是()cm。

9.一个扇形，半径是30cm，圆心角是60°，在平面上用1∶10的比例尺画出来，画出的扇形的半径是()cm，圆心角是()°。

10.在一幅地图上，量得甲、乙两地间的距离是7cm，乙、丙两地间的距离是9cm。

已知甲、乙两地间的实际距离是140km，这幅地图的比例尺是()，乙、丙两地间的实际距离是()km。

11.有12张扑克牌(同一副牌中不同花色的J、Q、K各4张)，洗一下反扣在桌面上，至少摸出()张牌才能保证有两张牌的颜色(红或黑)是相同的；至少摸出()张牌才能保证四种花色的牌都有；至少摸出( )张牌才能保证有三张牌是同一花色的。

12.一列高铁列车行驶的时间和路程如下图。

苏教版六年级数学下册单元培优测试卷第五单元确定位置一、填空。

(每空1 分，共28 分)1．(1) 公园在购物中心的( )偏( )( )° 方向600 米处。

(2) 购物中心在书店的( )偏( )( )° 方向( )米处。

(3)这幅图的比例尺是( )。

(4) 妈妈每天把球球送到学校后再去财富大厦上班。

某天妈妈送了球球后从学校到购物中心用了6 分，以同样的速度，妈妈再向( )偏( )( )°方向走( ) 分就能到达财富大厦。

2．如图，一艘轮船从海港O出发，以每时10 千米的速度沿( )偏( )( )°方向行驶了4 时后到达A 岛，然后以每时15 千米的速度沿( )偏( )( )°方向行驶了4 时后到达B岛。

这艘轮船从海港O出发经过A岛到达B岛一共航行了( )千米。

3．如图是中国象棋棋盘的一部分。

“炮”在“卒”的( ) 偏( )( )°方向上，距离是( )。

“马” 在“将”的( )偏( )( )°方向上，距离是( )。

若“将”在(4，0)，则在(5，1)北偏东45°方向上距离是3 厘米处的棋子是“( )”。

二、选择。

(将正确答案的字母填在括号里)(每小题3 分，共9 分)1．一架飞机从某机场向北偏东50°方向飞行了1200 千米，返回时要向( )。

A．北偏西40°方向飞行1200 千米B．南偏东50°方向飞行1200 千米C．南偏西40°方向飞行1200 千米D．南偏西50°方向飞行1200 千米2．体育馆在电影院的南偏东40°方向800 米处。

下面图( )能够正确反映体育馆和电影院的位置关系。

3．某机场的雷达屏幕如图所示，每相邻两个圆之间的实际距离为10 千米(最小的圆半径也是10 千米)。

以机场E 为观测点，飞机A 在北偏东30°方向距离机场E 30 千米处，下列描述错误的是( )。

鲁教版2021年度六年级数学下册《第五章基本平面图形》单元综合培优训练（附答案）1．如图，在直线l上有A、B、C三点，则图中线段共有（）A．1条B．2条C．3条D．4条2．如图，经过刨平的木板上的两个点，能弹出一条笔直的墨线，而且只能弹出一条墨线，能解释这一实际应用的数学知识是（）A．两点确定一条直线B．两点之间线段最短C．垂线段最短D．在同一平面内，过一点有且只有一条直线与已知直线垂直3．点C是线段AB的中点，点D是线段AC的三等分点．若线段AB＝12cm，则线段BD的长为（）A．10cm B．8cm C．10cm或8cm D．2cm或4cm4．如图（一），为一条拉直的细线，A、B两点在上，且：＝1：3，：＝3：5．若先固定B点，将折向，使得重叠在上，如图（二），再从图（二）的A 点及与A点重叠处一起剪开，使得细线分成三段，则此三段细线由小到大的长度比为何？（）A．1：1：1B．1：1：2C．1：2：2D．1：2：55．如图，钟表上10点整时，时针与分针所成的角是（）A．30°B．60°C．90°D．120°6．如图是雷达屏幕在一次探测中发现的多个目标，其中对目标A的位置表述正确的是（）A．在南偏东75°方向处B．在5km处C．在南偏东15°方向5km处D．在南偏东75°方向5km处7．1°等于（）A．10′B．12′C．60′D．100′8．如图，AM为∠BAC的平分线，下列等式错误的是（）A．∠BAC＝∠BAM B．∠BAM＝∠CAMC．∠BAM＝2∠CAM D．2∠CAM＝∠BAC9．直线上有2020个点，我们进行如下操作：在每相邻两点间插入1个点，经过3次这样的操作后，直线上共有个点．10．在修建崇钦高速公路时，有时需要将弯曲的道路改直，依据是．11．数轴上O，A两点的距离为4，一动点P从点A出发，按以下规律跳动：第1次跳动到AO的中点A1处，第2次从A1点跳动到A1O的中点A2处，第3次从A2点跳动到A2O 的中点A3处，按照这样的规律继续跳动到点A4，A5，A6，…，A n．（n≥3，n是整数）处，那么线段A n A的长度为（n≥3，n是整数）．12．如图，线段的长度大约是厘米（精确到0.1厘米）．13．在锐角∠AOB内部，画1条射线，可得3个锐角；画2条不同射线，可得6个锐角；画3条不同射线，可得10个锐角；…照此规律，画10条不同射线，可得锐角个．14．如图，平面内有公共端点的六条射线OA，OB，OC，OD，OE，OF，从射线OA开始按逆时针方向依次在射线上写出数字1，2，3，4，5，6，7，…．（1）“17”在射线上；（2）请任意写出三条射线上数字的排列规律；（3）“2007”在哪条射线上？15．在一条不完整的数轴上从左到右有点A，B，C，其中AB＝2，BC＝1，如图所示，设点A，B，C所对应数的和是p．（1）若以B为原点，写出点A，C所对应的数，并计算p的值；若以C为原点，p又是多少？（2）若原点O在图中数轴上点C的右边，且CO＝28，求p．16．先阅读下面的材料，然后解答问题：在一条直线上有依次排列的n（n＞1）台机床工作，我们要设置一个零件供应站P，使这n台机床到供应站P的距离总和最小，要解决这个问题先“退”到比较简单的情形．如图（1），如果直线上有2台机床时，很明显设在A1和A2之间的任何地方都行，因为甲和乙所走的距离之和等于A1到A2的距离．如图（2），如果直线上有3台机床时，不难判断，供应站设在中间一台机床，A2处最合适，因为如果P不放在A2处，甲和丙所走的距离之和恰好是A1到A3的距离，可是乙还得走从A2到P的这一段，这是多出来的，因此P放在A2处最佳选择．不难知道，如果直线上有4台机床，P应设在第二台与第3台之间的任何地方，有5台机床，P应设在第3台位置．问题：（1）有n台机床时，P应设在何处？（2）根据（1）的结论，求|x﹣1|+|x﹣2|+|x﹣3|+…|x﹣617|的最小值．17．考点办公室设在校园中心O点，带队老师休息室A位于O点的北偏东45°，某考室B 位于O点南偏东60°，请在图中画出射线OA，OB，并计算∠AOB的度数．18．用两种方法证明“三角形的外角和等于360°”．如图，∠BAE、∠CBF、∠ACD是△ABC的三个外角．求证∠BAE+∠CBF+∠ACD＝360°．证法1：∵，∴∠BAE+∠1+∠CBF+∠2+∠ACD+∠3＝180°×3＝540°∴∠BAE+∠CBF+∠ACD＝540°﹣（∠1+∠2+∠3）．∵，∴∠BAE+∠CBF+∠ACD＝540°﹣180°＝360°．请把证法1补充完整，并用不同的方法完成证法2．参考答案1．解：图中线段有AB、AC、BC这3条，故选：C．2．解：经过刨平的木板上的两个点，能弹出一条笔直的墨线，此操作的依据是两点确定一条直线．故选：A．3．解：∵C是线段AB的中点，AB＝12cm，∴AC＝BC＝AB＝×12＝6（cm），点D是线段AC的三等分点，①当AD＝AC时，如图，BD＝BC+CD＝BC+AC＝6+4＝10（cm）；②当AD＝AC时，如图，BD＝BC+CD′＝BC+AC＝6+2＝8（cm）．所以线段BD的长为10cm或8cm，故选：C．4．解：设OP的长度为8a，∵OA：AP＝1：3，OB：BP＝3：5，∴OA＝2a，AP＝6a，OB＝3a，BP＝5a，又∵先固定B点，将OB折向BP，使得OB重迭在BP上，如图（二），再从图（二）的A点及与A点重迭处一起剪开，使得细线分成三段，∴这三段从小到大的长度分别是：2a、2a、4a，∴此三段细线由小到大的长度比为：2a：2a：4a＝1：1：2，故选：B．5．解：∵钟面分成12个大格，每格的度数为30°，∴钟表上10点整时，时针与分针所成的角是60°．故选：B．6．解：由图可得，目标A在南偏东75°方向5km处，故选：D．7．解：1°等于60′．故选：C．8．解：∵AM为∠BAC的平分线，∴∠BAC＝∠BAM，∠BAM＝∠CAM，∠BAM＝∠CAM，2∠CAM＝∠BAC．故选：C．9．解：第一次：2020+（2020﹣1）＝2×2020﹣1，第二次：2×2020﹣1+2×2020﹣1﹣1＝4×2020﹣3，第三次：4×2020﹣3+4×2020﹣3﹣1＝8×2020﹣7．∴经过3次这样的操作后，直线上共有8×2020﹣7＝16153个点．故答案为：16153．10．解：在修建崇钦高速公路时，有时需要将弯曲的道路改直，依据是：两点之间线段最短．故答案为：两点之间线段最短．11．解：由于OA＝4，所有第一次跳动到OA的中点A1处时，OA1＝OA＝×4＝2，同理第二次从A1点跳动到A2处，离原点的（）2×4处，同理跳动n次后，离原点的长度为（）n×4＝，故线段A n A的长度为4﹣（n≥3，n是整数）．故答案为：4﹣．12．解：线段的长度大约是2.3（或2.4）厘米，故答案为：2.3（或2.4）．13．解：∵在锐角∠AOB内部，画1条射线，可得1+2＝3个锐角；在锐角∠AOB内部，画2条射线，可得1+2+3＝6个锐角；在锐角∠AOB内部，画3条射线，可得1+2+3+4＝10个锐角；…∴从一个角的内部引出n条射线所得到的锐角的个数是1+2+3+…+（n+1）＝×（n+1）×（n+2），∴画10条不同射线，可得锐角×（10+1）×（10+2）＝66．故答案为：66．14．解：（1）18正好转3圈，3×6；17则3×6﹣1；“17”在射线OE上；（2）射线OA上数字的排列规律：6n﹣5射线OB上数字的排列规律：6n﹣4射线OC上数字的排列规律：6n﹣3射线OD上数字的排列规律：6n﹣2射线OE上数字的排列规律：6n﹣1射线OF上数字的排列规律：6n（3）2007÷6＝334…3．故“2007”在射线OC上．15．解：（1）若以B为原点，则C表示1，A表示﹣2，∴p＝1+0﹣2＝﹣1；若以C为原点，则A表示﹣3，B表示﹣1，∴p＝﹣3﹣1+0＝﹣4；（2）若原点O在图中数轴上点C的右边，且CO＝28，则C表示﹣28，B表示﹣29，A 表示﹣31，∴p＝﹣31﹣29﹣28＝﹣88．16．解：（1）当n为偶数时，P应设在第台和（+1）台之间的任何地方，当n为奇数时，P应设在第台的位置．（2）根据绝对值的几何意义，求|x﹣1|+|x﹣2|+|x﹣3|+|x﹣617|的最小值就是在数轴上找出表示x的点，使它到表示1，617各点的距离之和最小，根据问题1的结论，当x＝309时，原式的值最小，最小值是308+307+…+1+1+2+…+308＝95172．17．解：∵∠1＝45°，∠2＝60°，∴∠AOB＝180°﹣（45°+60°）＝75°．18．证明：证法1：∵平角等于180°，∴∠BAE+∠1+∠CBF+∠2+∠ACD+∠3＝180°×3＝540°，∴∠BAE+∠CBF+∠ACD＝540°﹣（∠1+∠2+∠3）．∵∠1+∠2+∠3＝180°，∴∠BAE+∠CBF+∠ACD＝540°﹣180°＝360°．证法2：∵∠BAE＝∠2+∠3，∠CBF＝∠1+∠3，∠ACD＝∠1+∠2，∴∠BAE+∠CBF+∠ACD＝2（∠1+∠2+∠3），∵∠1+∠2+∠3＝180°，∴∠BAE+∠CBF+∠ACD＝360°．故答案为：平角等于180°，∠1+∠2+∠3＝180°。

小学六年级数学培优练习题（一）一、还原应用题1. 一堆煤，第一次运走总的21多4吨，第二次运走余下的50℅多6吨，第三次运走8吨刚好运完，这堆煤原有多少吨？2. 一堆苹果，小明分得总的21多8个，小华分得余下的21多10个，小东分得余下的21多6个，结果还剩下4个，这堆苹果原有多少个？3. 一袋大米，吃去它的101后又放回10℅，这时重99千克，这袋大米原重多少千克？ 4. 一种电视机，先降价10℅，后又提价101出售价是1980元，这种电视机原价多少元？二、抓住不变量解应用题1. 某工厂原有工人450人，其中女工占259，今年又招进一部分女工，这时女工人数占全厂人数的40℅.求今年招进女工多少人？2. 某校六年级有学生50人，其中女生占40℅,后来又转入几名女生，这时女生人数和男生人数比是5︰6，求转入几名女生？3. 图书室有一批科技书和文艺书共1500本，其中科技书占52，后来又买回部分科技书，这时，文艺书占总数的52，求买回科技书多少本？小学六年级数学培优练习题（二）三、不同单位“1”的转化应用题（一）1. 甲乙两堆煤共有330吨，甲堆的32等于乙堆的41，求甲乙两堆煤原来各有多少吨？ 2. 甲乙两人共生产零件140个，已知甲生产个数的25℅等于乙生产个数的31，求甲乙各生产零件多少？3. 甲乙两个书架共有书270本，从甲书架借走54，又从乙书架借走75℅，这时两书架余下的书相等，求两书架原有书多少本？4. 甲乙两数和是190，甲数小数点向左移动一位后等于乙数的83，甲乙两数原来各是多少？ 5. 甲乙两数和是110，甲数减少20℅,乙数增加52后相等，求甲乙两数原来各是多少？ 6. 有A 、B 两个粮仓，A 仓比B 仓存粮少30吨，运走A 仓的60℅,又运走B 仓的43后，两仓余下的粮相等，求A 、B 两仓原有粮多少吨？7. 甲乙两个粮仓，甲仓重量的75℅与乙仓重量的53相等，如果从乙仓调出10吨到甲仓，这时两仓存粮相等，求原来甲乙两仓存粮各有多少吨？小学六年级数学培优练习题（三）四、不同单位“1”的转化应用题（二）1. 六年级班女生是男生的30℅,后来又转来10名女生，这时女生是男生的52，求原来六年级班有多少人？ 2. 某车间女职工人数占车间总人数的2512，后来增加了22名女职工，这时女职工人数占车间总人数的70℅,求这个车间原有多少人？3. 学校体育队中女生人数是男生的75℅,后来又增加了4名男生，这时女生人数是男生的32，求体育队现在有多少人？4. 小明读一本故事书，第一天读了120页，第二天读了余下的103，这时两天共读的页数占总页数的40℅,这本书有多少页？5. 某工程队修一条路公路，第一天修了160米，第二天修了余下的25℅,修了两天后，已修的长度与剩下的长度比是3︰5，这条公路长多少米？6 .一个车间，男女职工人数比是5︰7，后来又调进男职工20人，这时男女职工人数比是7︰9，这个车间现有男职工多少人？小学六年级数学培优练习题（四）五、不同单位“1”的转化应用题（三）1.甲乙两书架共有书1000册，已知甲书架上书的31比乙书架上书的50℅多50册，问甲乙书架一原来各有书多少本？ 2. 有甲乙两个粮仓欠存粮210吨，甲仓存粮的50℅比乙仓存粮的52多60吨，求甲乙两仓原存粮各多少吨？3. 甲乙两个班共有62人参加科技活动，甲班参加人数的51比乙班参加人数的25℅少2人，求甲乙两个班原来各有多少人参加科技活动？4. 光明小学有学生1600人，男生人数的20℅比女生人数的41少40人，求男女生人数各有多少人？ 5. 东风小学有学生360人，男生人数的52比女生人数的25℅多40人，求男、女生名有多少人？小学六年级数学培优练习题（五）六、不同单位“1”的转化应用题（四）1. 有一堆煤，已运的占未运60℅,如果再运40吨，已运的和未运的一样多，这堆煤有多少吨？2. 小英读一本书，已读的是未读的52，如果再33页，已读的是未读的60℅,这本书有多少页？ 3. 李师傅加工一批零件，已加工的是没有加工的37.5℅,如果再加工84个，恰好完成任务的52，李师傅已加工了多少个零件？4. 六（1）班参加课外活动，参加航模的人数是其他活动人数的20℅,后来又有2人参加航模活动，这时航模人数是其他活动人数的25℅,求这次活动有多少人参加？5. 幼儿园四个班分一堆苹果，一班分得是其他三班的21，二班分得是其他三班的31，三班分得是其他三班的41，四班分得26包，这堆苹果有多少包？6. 一个商店三天卖完一批电视，第一天卖的是余下的31，第二卖了21部，第三天卖的和总数比是2︰5，这批电视有多少部？小学六年级数学培优练习题（六）七、用假设法解分数应用题1. 甲乙两个工程队共有336人，抽调甲队人数的75和乙队人数的73共188人支援另外工程，求甲乙工程队原来各有多少人？2. 有文艺和科技两个兴趣小组共90人，文艺组人数的74与科技组人数的32共54人，文艺小组和科技小组各有多少人？3 . 东风小学举行数学竞赛，参赛有150人，获奖有26人，男生获奖人数占男生参加人数的51，女生获奖人数占女生人数的15℅.求参加竞赛的男、女生各有多少人？4. 中夏化工总厂有两堆煤，共重2268千克，取出甲堆的40℅,和乙堆的14 共重708千克。

六年级小升初数学培优试卷测试卷（附答案解析）一、选择题1．在地图上量得两地距离为5厘米，表示实际距离150千米，这幅地图的比例尺是（）A．1：30 B．1：3000 C．1：30000002．一个长方体高为36cm，其底面为正方形，边长为6cm，现把它都切割成棱长为6cm的正方体，表面积将（）。

A．增加360cm2B．减少360cm2C．减少216cm2D．增加216cm2 3．计算下图阴影部分的面积．正确的算式是（）．A．3.14×6-3.14×4 B．3.14×（3-2）C．3.14×（32-22）4．一个三角形三个内角度数的比是4∶3∶2，这个三角形是（）。

A．钝角三角形B．等腰三角形C．直角三角形D．锐角三角形5．5千克棉花的和1千克铁的比较，结果是（）A．5千克棉花的重B．1千克铁的重C．一样重D．无法比较6．莉莉用同样大的正方体摆成了一个长方体。

下图分别是她从正面和上面看到的图形。

从右面看到的是下面（）图形。

A．B．C．7．下面说法错误的是（）。

A．两种量相对应的两个数的比值－定，这两种量之间就是正比例关系。

B．同一幅地图，图上距离和实际距离之间成正比例关系。

C．如果两种相关联的量相对应的两个数的乘积一定，它们之间就是反比例关系。

D．两种相关联的量之间，不一定存在正比例或反比例关系。

8．a是奇数，b是偶数，下面结果是奇数的式子是（）。

A．a＋b B．2a＋b C．2（a＋b）9．一件商品提价10％以后又降价10％，现在这件商品的价格是原来价格的百分之几？正确的解答是（）A．110％B．90％C．100％D．99％10．观察图中每一个大三角形中白色的三角形的排列规律，则第5个大三角形中白色的三角形有（）A．82个B．154 C．83个D．121个二、填空题11．910千米＝（________）米712时＝（________）分十12．325的分数单位是（________），它有（________）个这样的分数单位，再去掉（________）个这样的分数单位就是最小的质数。

小学六年级小升初数学质量培优试题测试题（附答案解析）一、选择题1．一张地图的比例尺是1∶25000,从图中测得两地的距离是4cm,它们的实际距离是()km．A．1 B．10 C．100 D．1000002．李华的座位用数对表示是（4，5），刘玲的座位在李华的东偏南45°方向上，她的座位可能是（）。

A．（3.4）B．（5，4）C．（5，6）3．王师傅和李师傅合做完成一批零件，王师傅单独完成需要4小时，李师傅单独完成需要5小时，如果两人合做，需要几小时完成这批零件？正确的算式是()．A．(4＋5)÷2 B．1÷(4＋5) C．1÷(＋)4．一个三角形三个内角度数的比是2:3:5，这个三角形中最大的内角是（）。

A．锐角B．直角C．钝角5．根据“衣服比裤子贵50元，衣服是裤子价格的3倍，”下列方程正确的是（）（设裤子价格为X元）。

A．3x+x=50 B．3x－x=506．如图是一个正方体的平面展开图，在这个正方体中，与“2”相对的面是（）。

A．1 B．3 C．67．下图是将一个圆柱体切拼成一个近似的长方体，比较二者，下面说法中错误的是（）。

A．底面积相等B．高相等C．表面积相等D．体积相等8．如图将一个圆柱转化成一个长方体、体积（）。

A．不变B．增加C．减少9．某城市的士票价为：租单程3km以内8元，超过3km的部分每千米2.5元；如果租往返每千米2元．下面的图（）表示租单程时路程与收费的关系，（）表示租往返时路程与收费的关系．A．B．C．D．10．红红按照一定的规律用小棒摆出了下面的4幅图如果按照这个规律维续摆，第五幅图要用（）根小棒。

A．23 B．31 C．35 D．45二、填空题11．海王星与太阳之间的平均距离大约是4504000000千米。

这个数读作（________），改写成用“万”作单位的数是（________）万，省略“亿”后面的尾数约是（________）亿。