当前位置：文档之家 › 4定常管流的压力损失计算_简

4定常管流的压力损失计算_简

  • 格式：ppt
  • 大小：617.50 KB
  • 文档页数：21

下载文档原格式

  / 21

合集下载

《工程流体力学》第四章 流动损失

《工程流体力学》第四章 流动损失
只有当惯性力（升力或沉力）的作用比粘性阻力作用大到 一定程度时，旋涡才可能迁移、掺混和发展，使层流变为 紊流。
层流受到扰动后 主导作用：粘性稳定作用 粘性稳定作用：使扰动衰减下来 流动：变为层流 主导作用：惯性扰动作用 粘性作用：无法使扰动衰减下来 流动：变为紊流
雷诺数正是反映了惯性力和粘性力的对比关系， 能判别流态。
在波峰上侧断面受压缩，流动截面积A变小，流速V增加， 压强p变小 在波峰下侧与上侧相反，A增加，V变小，p增加
在波谷上侧断面，A增加，V变小，p增加 在波谷下侧断面，A变小， V增加，p变小
结果出现由波谷指向波峰的两种压差Dp，Dp’
其中Dp使波动弯曲加剧，波幅增大； 而Dp’大到一定程度后，使流线两侧产生从波谷向另一波 峰流动的二次流，其作用是使波谷处受吸力，波峰处有惯 性力。
2、运动参数的时均值： 时均流速V：某点瞬时速度V在足够长时间段内的平均值
流速脉动－>切应力、压强也产生脉动 如，对压强同样有：
对时均流动和脉动流动分别进行研究。
定常紊流流动：对时均流动，时均速度和时均压强不随时 间而变的紊流流动。 有关定常流动规律，如连续方程、伯努利方程等都可用。
但紊流中还要考虑脉动影响 脉动－>横向掺混－>各流层间质量、动量、热量和悬浮 含量的分布大大平均化 动量交换－>紊流阻力大大增加 紊流脉动速度时均值：0 在工程上采用紊流度概念：表示紊流随机性质
Q流速高于VK的流动状态：极不稳定，稍有扰动，就转变 为紊流，对实际工程来说，总是有扰动的。 上临界速度对工程实际没有意义，而下临界速度就成为 判断流态的界限。 下临界速度也被称为临界速度。
雷诺实验还揭示了不同流动状态下流动损失规律。 不同流速下截面1到截面2的流动损失hw：画在对数坐标上

液压传动基础

液压传动基础
Ft du A dy
3）粘度旳种类 1）动力粘度：又称绝对粘度，动力粘度μ
旳物理意义是，液体在单位速度梯度下 流动时单位面积上产生旳内摩擦力 2）运动粘度：液体旳动力粘度与其密度旳 比值
v=μ/ρ
3）相对粘度：相对粘度又称条件粘度，它 是按一定旳测量条件制定旳。可分为恩氏 粘度°E、赛氏粘度SSU、雷氏粘度Re等。
按帕斯卡原理，液压缸内压力到处相等，
p1≈p2＝p，于是 F2＝F1A2/A1
五、液体静压力对固体壁面旳作用力
1）当固体壁面为平面时，液体压力在该平面 旳总作用力 F = p A ，方向垂直于该平面。
2）当固体壁面为曲面时，液体压力在曲面某 方向上旳总作用力 F = p Ax ， Ax 为曲面 在该方向旳投影面积
旳压力； （2）相对压力—— 以大气压力作为基准所 表达旳压力
• 绝对压力＝相对压力 ＋大气压力
• 真空度＝大气压－绝对压力 2.压力旳单位: 我国法定压力单位为帕斯卡，简称帕 1MPa = 106 Pa 1at（工程大气压）=1kgf/cm2=9.8×104 Pa 1mH2O(米水柱)=9.8×103 Pa 1mmHg(毫米汞柱)=1.33×102 Pa 1bar(巴) = 105 Pa≈1.02kgf/cm2
s1 )
dq dt
q 2 v 2
q1v1
(1-31)
β为动量修正系数
2）物理意义
• 方程左边为作用于控制体积内液体上旳全部外力 旳总和
• 等式右边第一项表达液体流量变化所引起旳力， 称为瞬态力
• 第二、三项表达流出控制表面和流入控制表面时 旳动量变化率，称为稳态力
• 定常流时：
F q2v2 q1v1
第三节 液体动力学

液体静力学

液体静力学

流体力学基础一、 液体静力学液体静力学主要是讨论液体静止时的平衡规律以及这些规律的应用。

所谓“液体静止”指的是液体内部质点间没有相对运动，不呈现粘性而言，至于盛装液体的容器，不论它是静止的还是匀速、匀加速运动都没有关系。

1、液体静压力及其特性当液体静止时，液体质点间没有相对运动，不存在摩擦力，所以静止液体的表面力只有法向力。

液体内某点处单位面积△A 上所受到的法向力△F 之比，称为压力p （静压力），即由于液体质点间的凝聚力很小，不能受拉，只能受压，所以液体的静压力具有两个重要特性：液体静压力的方向总是作用在内法线方向上；静止液体内任一点的液体静压力在各个方向上都相等。

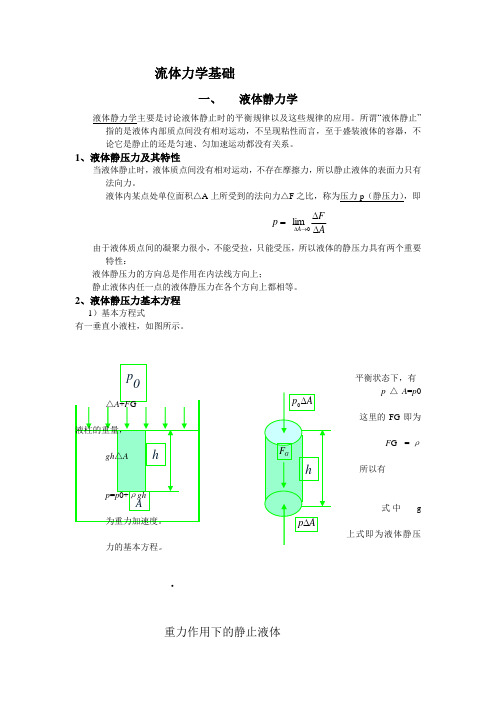
2、液体静压力基本方程1）基本方程式有一垂直小液柱，如图所示。

平衡状态下，有p △A =p 0这里的FG 即为F G =ρ所以有式中 g上式即为液体静压力的基本方程。

·重力作用下的静止液体由液体静压力基本方程可知:A、静止液体内任一点处的压力由两部分组成，一部分是液面上的压力p0，另一部分是ρg与该点离液面深度h的乘积。

当液面上只受大气压力p a作用时，点A处的静压力则为p=p a+ρgh。

B、同一容器中同一液体内的静压力随液体深度h的增加而线性地增加。

C、连通器内同一液体中深度h相同的各点压力都相等。

由压力相等的组成的面称为等压面。

在重力作用下静止液体中的等压面是一个水平面。

2）静压力基本方程的物理意义静止液体中单位质量液体的压力能和位能可以互相转换，但各点的总能量却保持不变，即能量守衡。

3）帕斯卡原理根据静压力基本方程(p=p0+ρgh),盛放在密闭容器内的液体，其外加压力p0发生变化时，只要液体仍保持其原来的静止状态不变，液体中任一点的压力均将发生同样大小的变化。

这就是说，在密闭容器内，施加于静止液体上的压力将以等值同时传到各点。

这就是静压传递原理或称帕斯卡原理。

即：压力的传递关系3、压力的表示方法及单位1）压力的表示法有两种：绝对压力和相对压力。

流体力学流动效率计算公式

流体力学流动效率计算公式

流体力学流动效率计算公式流体力学是研究流体在运动中的力学性质和规律的一门学科。

在工程领域中，流体力学的研究对于设计和优化流体系统具有重要意义。

流动效率是评价流体系统性能的重要指标之一，它反映了流体在管道或设备中的运动效果和能量损失情况。

在工程实践中，我们常常需要计算流动效率来评估流体系统的性能，并根据计算结果进行优化设计。

本文将介绍流体力学流动效率的计算公式及其应用。

1. 流动效率的定义。

流动效率是指流体在管道或设备中的运动效果和能量损失情况。

在实际工程中，流动效率通常用流动的能量损失与输入的能量之比来表示，即流动效率=输出能量/输入能量。

流动效率的计算可以帮助工程师了解流体系统的性能状况，找出能量损失的原因，并进行优化设计。

2. 流动效率的计算公式。

流动效率的计算公式可以根据具体的流体系统和流动情况来确定。

一般来说，流动效率的计算公式可以分为两种情况，定常流动和非定常流动。

（1）定常流动情况下的流动效率计算公式。

在定常流动情况下，流动效率可以用流体在管道或设备中的能量损失与输入的能量之比来表示。

假设流体在管道中的能量损失为ΔP，输入的能量为P，那么流动效率η可以表示为：η = (P-ΔP)/P。

其中，ΔP为流体在管道中的能量损失，P为输入的能量。

（2）非定常流动情况下的流动效率计算公式。

在非定常流动情况下，流动效率的计算相对复杂一些。

一般来说，可以利用流体动力学方程和能量守恒方程来进行计算。

非定常流动情况下的流动效率计算公式可以表示为：η = (W-ΔW)/W。

其中，W为输入的能量，ΔW为流体在管道中的能量损失。

3. 流动效率的应用。

流动效率的计算可以帮助工程师评估流体系统的性能，找出能量损失的原因，并进行优化设计。

在实际工程中，流动效率的应用非常广泛，下面以几个具体的应用场景来介绍流动效率的应用。

（1）管道流动效率的计算。

在管道流动中，流动效率的计算可以帮助工程师了解管道中的能量损失情况，找出能量损失的原因，并进行管道的优化设计。

压降计算公式

压降计算公式

压降计算公式压降（pressuredrop）是流体运动过程中发生的非质量的损耗，一般用来衡量流体在管路中的能量消耗，也就是压力消耗。

在流体运动过程，随着流体流经管道，管内摩擦阻力大小与流体运动速度和管道内阻力有关，管系中存在不可忽视的压力损失。

因此，需要对管道系统的压降进行计算以便对其进行设计和操作。

压降（pressure drop）的计算一般通过流体力学的basic equations来进行。

它们主要包括流体动量守恒方程、能量守恒方程和流体流量定律。

根据这些方程，我们可以得到压力损失的计算公式，也就是所谓的压降计算公式。

压降计算公式通常有以下三种形式：1. Darcy-Weisbach公式Darcy-Weisbach方程又称摩擦因数公式，Darcy-Weisbach方程表示流体在管道内的压降损失，它可以用来计算几乎任何形式的流体在任何形状管道中的压力损失。

它的公式为：ΔP=f*L*V2/2D（单位：帕）其中，ΔP表示压力损失，f表示摩擦系数，L表示管道长度，V 表示流速，D表示管道内径。

2.壁阻力非定常公式管壁阻力非定常公式旨在试图分离流体的摩擦力和管壁阻力，以改善管道压力损失的计算。

它的公式为：ΔP=f*L*V2 /2D+t*L*V2/2D其中，ΔP表示压力损失，f表示摩擦系数，L表示管道长度，V 表示流速，D表示管道内径，t表示管壁阻力系数。

3. Cole-Cole-Cole公式Cole-Cole-Cole公式是一种计算压降的更精确方法，它可以更详尽地考虑流体管道系统中的摩擦力和管壁阻力。

它的公式为：ΔP = [ f1 * L * V2 / 2D + k1 * V2] + [ f2 * L * V2 / 2D + k2 * V2]其中，ΔP表示压力损失，f1和f2表示摩擦系数，L表示管道长度，V表示流速，D表示管道内径，k1和k2表示管壁阻力系数。

以上就是压降计算公式的常见表达形式，为了更加准确地计算出系统中的压力损失，还需要考虑流体的流量、粘度、温度和密度等因素，以及考虑管道的实际形状、材料和粘滞性等因素。

压力损失

压力损失

•
hf

p1 p2 g

p g
（4-8）
•
又由达西公式：
• •
hf

LV2 d 2g
• 比较式（4-7）、（4-8）、（4-9），可得：
（4-9）
•
0


8
V
2
（4-10）
4.不可压缩粘性流体一元流动
•
上式V为截面平均速度。引入摩擦速度u*：
•
u*
0
（4-11）
• •
式（4-10）可写为：
• 实验配置：
• 1：盛有无色水的大容器，
•
液位高保持不变。
• 2：透明等直径管。
• 3：盛有有色水的小容器。
• 4：阀门。
• 5、6：两个测压管。
3 1
5
hf
6 4
2
• 实验过程：
• （1）打开阀门4，管内流速由小变大，当水以较低速度流过透明管。管 中有色水近似呈直线状流动，说明管中水流的质点以一种有规则的、互 不混杂的形式作分层流动。这种流动状态称为层流。
•
轴线上，并且为：
um

p L
r02
4
（4-16）
u
um
•
由截面速度分布，还可计算出通过管截面上的体积流量Q。
•
Q r0 2rudr p r04
0
L 8
（4-17）
4.不可压缩粘性流体一元流动
•
管截面平均速度V：
•
V

Q r02

p L
r0 2 8

1 2 um
•
故截面速度分布也可用平均速度来表示：

《液压传动与气动技术》课程标准

《液压传动与气动技术》课程标准一、课程定位1.课程性质必修课；专业课（含实验课）。

2.课程作用《液压传动与气动技术》是机电一体化技术专业的一门重要的专业技术课程。

无论对学生的思维素质、创新能力、科学精神以及在工作中解决实际问题的能力的培养，还是对后继课程的学习，都具有十分重要的作用。

该课程主要研究液压与气压传动技术一般规律和具体应用的一门科学。

这门技术与其它传动形式有不可比拟的优势而应用广泛，以优良的静态、动态性能成为一种重要的控制手段，无论是机械制造、模具、数控，还是自动化都有广泛的实际应用价值。

该课程实现了高职的培养目标，满足了机电类教育人才的要求，是专业教学必不可少的重要组成部分。

二、课程目标通过本课程的学习，使学生较系统地掌握液压气动技术的基本原理和实际应用。

获得基本的理论基础知识、方法和必要的应用技能；认识到这门技术的实用价值，增强应用意识；逐步培养学生学习专业知识的能力以及理论联系实际的能力，为学习后继课程和进一步学习现代科学技术打下专业基础；同时培养学生的创新素质和严谨求实的科学态度以及自学能力。

具体目标：1、知识目标职业能力要求（1）能较好的掌握液压与气压传动的基本概念和基础知识；（2）能较好的掌握液压与气压元件的功用、组成、工作原理和应用；（3）能教好的掌握液压与气压回路的组成和功能；2、能力目标（1）具有阅读并分析典型液压与气压传动系统组成、工作原理及特点的能力；（2）具有初步的液压与气压传动系统调试和排故的能力。

；（3）通过网络、期刊、专业书籍、技术手册等获得信息能力，收集资料的能力；（4）具有制定、实施工作计划的能力；3、素质目标（1）具有团队协作的意识，良好的小组成员协作能力；（2）具备良好沟通能力和评价他人的能力；（3）正确面对困难和挫折的处理能力；（4）负责任的工作习惯；（5）节约并保护环境的意识；三、课程设计一、设计思想教学内容框架（1）坚持以高职教育培养目标为依据，基于本课程在机电类专业知识、能力构筑中的位置及这门技术的特点，突出应用能力和综合素质培养，充分注意“教、学、做”三结合。

液体流动的力学规律


静压力基本方程是伯努利方程的特例
实际液体的伯努利方程
p1
g
z1
1 2g
112
p2
g
z2
1 2g
2
22
hw
α:动能修正系数,为截面上单位时间内流过液体所具有 的实际动能，与按截面上平均流速计算的动能之比（层
流时α=2，紊流时α=1）
hw:单位重量液体所消耗的能量
伯努利方程应用实例
液压泵吸油口处的真空度是油箱 液面压力与吸油口处压力p2之差。
128lq p d 4
p
64 Re
l d
2
2
l
d
2
2
λ:沿程压力损失系数,其理论值为 . 64 Re
当流动液体为液压油时， 75 Re
1.4.2 定常管流的压力损失
局部压力损失Δpξ : 在流经阀口、管道截面变化、 弯曲等处时，由于流动方向和速度变化及复杂的流动现象(旋涡， 二次流等)而造成局部能量损失
p
2
2
ξ称为局部压力损失系数
1.4.2 定常管流的压力损失
管路系统的压力损失和压力效率 :整个管路系
统的总压力损失是系统中所有直管的沿程压力损失和所有局部压
力损失之和
n pi
i1
k
i
i1
li di
2 i
2
n
i
ik 1
i2
2
使用条件:管路系统中两相邻局部压力损失之间距离足够大
（相连管径的10-20倍）
液压泵吸油口处的真空度却不能 太大. 实践中一般要求液压泵的 吸油口的高度h不超过0.5米.
图2-10 液压泵从油箱吸油
1.4 管路系统流动分析

分析定常流体在管道中的流速与压力分布

分析定常流体在管道中的流速与压力分布在工程领域中，了解流体在管道中的流速与压力分布对于设计和操作管道系统至关重要。

定常流体是指在管道内流动过程中流速与压力分布不随时间变化的流体。

本文将针对定常流体在管道中的流速与压力分布进行分析。

首先，定常流体在管道中的流速分布受到一系列因素的影响。

其中最重要的因素是管道的几何形状、流量、液体性质和管道壁面条件。

管道的几何形状包括管道的长度、直径、弯曲及管壁粗糙度等。

流量则与液体的质量流速和管道截面积有关。

此外，液体的性质如黏度、密度和温度也会对流速分布产生影响。

最后，管道壁面的条件会引起流体附着、摩擦和湍流等现象，从而改变流速分布。

其次，管道中定常流体的流速分布可以通过流量连续性方程和能量守恒方程来计算。

流量连续性方程是根据质量守恒定律推导得到的，用于描述流体在管道中不同截面上的质量流量相等。

能量守恒方程则是根据能量守恒定律推导得到的，用于描述流体在管道中不同截面上的压力变化情况。

通过解这两个方程，可以得到定常流体在管道中的流速分布。

对于简单的管道系统，可以使用流体力学基本原理进行定常流体流速分布的计算。

例如，对于水平管道中的层流流动，流速分布可以通过哈根—珀洛兹公式进行计算。

这个公式是由实验数据得出的经验公式，根据管道的几何形状和液体性质计算流速分布。

对于湍流流动，可以使用摩擦因子、雷诺数和流动参数等来计算流速分布。

此外，压力分布是定常流体流动中另一个重要参数。

压力分布受到流体的阻力、摩擦、惯性和引力等因素的影响。

在水平管道中，液体的重力对压力分布起主要作用，而在垂直管道中，液体的惯性对压力分布起主要作用。

对于层流流动，可以通过泊肃叶公式进行压力分布的计算。

该公式基于质量守恒方程和能量守恒方程，结合斯托克斯流动定律进行推导。

对于湍流流动，可以使用雷诺应力和湍流能量方程等进行压力分布的计算。

最后，对于复杂的管道系统，一般需要使用数值模拟方法，如计算流体力学（CFD）来计算定常流体的流速与压力分布。

管内流动和水力计算


第三节
管道进口段中粘性流体的流动
一、圆管内层流流动的起始段
d
L
层流边界层
充分发展的流动
紊流边界层
d
L
粘性底层
由于流体的粘性作用，自圆管入口起，在管壁附近形成一层 有速度梯度存在的流体薄层，该流体薄层内壁面上流体的速 度为零，薄层外边界上的流速为u (x)。这一有速度梯度存在 的流体层称为附面层或边界层。 从管进口到附面层在管中心汇合处的截面间的一段距离L*称 为层流(紊流）的起始段。以下将证明，在起始段以后的各管 截面上的速度分布均为抛物线分布(对数曲线)。起始段以后 的管段称为层流（紊流）的充分发展段。
阻力的方式和大小，以及对传热传质过程和动量传递规律等都
各不相同，所以在研究这些问题之前，首先需要判别流体的流 动是属于哪一种状态。
说明
实验结果表明，对于光滑的圆截面直管，不论流体的性质和管
径如何变化，其下临界雷诺数一般均为Rec=2100～2300，
而上临界雷诺数Recr′可达12000～13800，甚至更高些， 但这时流动处在极不稳定的状态，稍有扰动层流瞬即被破坏而 转变为紊流。因此，上临界雷诺数在工程上没有实用意义，通 常用下临界雷诺数来判别流体的流动状态，即取圆管内流动的
r0 p 2l
r dp r p r p 2 dl 2 l 2l
p p1 p2 dp 没有负号
l v2 由前述： p d 2
代如上式得：
w

8
v2
二、速度分布.
根据牛顿内摩擦定律： dvl ,
dr
1 d dvl ( p gh)rdr 2 dl
2 0 a 4 0
d p ( p gh) 对于水平圆管： dl l
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
16
p1 A1 + p0 ( A2 − A1 ) − p2 A2 = ρq (v2 − v1 )
由试验知： 由试验知：p0=p1
( p1 − p2 ) A2 = ρA2 v2 (v2 − v1 )
A2 p1 − p2 = ρv (1 − ) A1
2 2
2 ρv2 A2 2 A2 2 ∆pr = hr ρg = ρv2 (1 − ) + [( ) − 1] A1 A1 2
260 20～100
6
对于非圆截面管道
运动 速度 水力 半径 有效截 面积
4νR Re = v
运动 黏度
A R= x
湿周
水力半径对管道通流能力影响很大， 水力半径对管道通流能力影响很大， 水力半径大，表明液流与管壁接触少， 水力半径大 ， 表明液流与管壁接触少 ， 通流 能力大； 能力大； 水力半径小，表明液流与管壁接触多， 水力半径小 ， 表明液流与管壁接触多 ， 通流 能力小，易堵塞。 能力小，易堵塞。 7
19
由于存在压力损失， 由于存在压力损失，一般液压系统中液 压泵的压力p 压泵的压力 p应比执行元件的工作压力 p1高∑△p，即 △ ，
p p = p1 + ∑ ∆p
所以管路系统的压力效率为
η Lp
p p + ∑ ∆p p1 = = = 1− pp pp
∑ ∆p
ppБайду номын сангаас
20
五、减少液压系统中的压力损失的办法 压力损失产生的影响： 压力损失产生的影响：
du τ = −µ dr
积分可得
p1 − p 2 2 u=− r +C 4 µl
10
由边界条件：当r=d/2时，u=0，可得积分常数C， 由边界条件： 时 ，可得积分常数 ， 即
p1 − p2 2 C= d 16µl
代入上式可得
p1 − p2 d 2 u= ( −r ) 4 µl 4
2
当r=0处（即管道中心）流速最大，其值为 r=0 即管道中心）流速最大，
q ∆ p = ( ) qn
2
∆ p
n
18
四、管路系统中的总压力损失与压力效率
管路系统中的总的压力损失等于所有直管 中的沿程压力损失和局部压力损失之和， 中的沿程压力损失和局部压力损失之和 ， 即
l ρv 2 ρv 2 ∑ ∆p = ∑ λ d 2 + ∑ζ 2
实际数值比上式计算出的压力损失大。 实际数值比上式计算出的压力损失大。
二、液体在直管中流动时的压力损失 沿程压力损失： 沿程压力损失：液体在直管中流动时的 压力损失。 压力损失。 它除与管道的长度、内径和液体的流速、 它除与管道的长度、内径和液体的流速、 粘度等有关外，还与液体的流动状态有关。 流动状态有关 粘度等有关外，还与液体的流动状态有关。 液体在圆管中的层流流动是液压传动中 最常见的现象， 最常见的现象，在设计和使用液压系统时 就希望管道中的液流保持这种状态。 就希望管道中的液流保持这种状态。
13
（二）紊流时的压力损失
紊流流动现象 很复杂的。 很复杂的。 紊流状态下液 体流动的压力 损失仍用上式 来计算。 来计算。 式中的λ值不仅 式中的 值不仅 与雷诺数Re有 与雷诺数 有 关，而且与管 壁表面粗糙度 有关。 Δ有关。
雷诺数Re 雷诺数
λ值的计算公式 值的计算公式
Re＜22 ＜ （d/△）8/7 △
8
（一）层流时的压力损失
1、 液流在通流截面上的速度分布规律
r τ d
dr
r
p1 τ
l
p2
u
圆管中的层流
9
在管道中取一轴线与管道轴线重合的微小圆柱体， 在管道中取一轴线与管道轴线重合的微小圆柱体 ， 在轴线方向上的受力平衡方程为
( p1 − p2 )π r 2 − 2π rlτ = 0
由牛顿内摩擦定律可知
1
一、流态、雷诺数 流态、
1．层流和紊流 动画 层流和紊流(动画 层流和紊流 动画)
2
雷诺实验结果
b）层流开始破坏 a）层流
c）流动趋于紊流
d）紊流
3
层流：液体质点互不干扰 ， 层流 液体质点互不干扰， 液体的流动呈线性 液体质点互不干扰 或层状，且平行于管道轴线；层流时， 或层状，且平行于管道轴线；层流时，液体流 速较低，质点受粘性制约，不能随意运动， 速较低，质点受粘性制约，不能随意运动，粘 性力起主导作用。 起主导作用。 紊流：液体质点的运动杂乱无章 ， 除了平行于 紊流 液体质点的运动杂乱无章， 液体质点的运动杂乱无章 管道轴线的运动以外，还存在着剧烈的横向运 管道轴线的运动以外， 紊流时，液体流速较高， 动；紊流时，液体流速较高，粘性的制约作用 减弱， 起主导作用。 减弱，惯性力起主导作用。 液流状态究竟是层流还是紊流，用雷诺数来判定。 液流状态究竟是层流还是紊流，用雷诺数来判定。 究竟是层流还是紊流
5
常见液流管道的临界雷诺数
管道的形式 光滑的金属圆 管 橡胶软管 临界雷诺 数 2000～ ～ 2300 1600～ ～ 2000 1100 1000 管道的形式 有环槽的同心环 状缝隙 有环槽的偏心环 状缝隙 临界雷诺 数 700 400
光滑的同心环 状缝隙 光滑的偏心环 状缝隙
圆柱形滑阀阀口 锥阀阀口
三、局部压力损失
局部压力损失是液体流经如阀口、弯管、 局部压力损失是液体流经如阀口 、弯管 、 通流截面变化等局部阻力处所引起的压力 损失。 损失。局部压力损失的计算公式为
∆pr = ζ
ρv
2
2
ζ 为 局部阻力系数 ， 一般由实验确定 ， 也可查阅有 一般由实验确定， 关液压传动设计手册； 为液体的平均流速， 关液压传动设计手册； v为液体的平均流速， 一般 情况下均指局部阻力后部的流速。 情况下均指局部阻力后部的流速。
umax
p1 − p2 2 = d 16µl
11
2．圆管中的流量
对上式积分即可求得通过整个通流截面的流量
q = ∫ udA = ∫
A
d 2 0
p1 − p2 d 4 πd 4 ( − r 2 )2πrdr = ∆p 4 µl 4 128µl
2
平均 流速
q d v= = ∆p A 32 µl
液体在圆管中作层流流动时， 液体在圆管中作层流流动时，其中心处的最大 流速正好等于其平均流速的两倍， 流速正好等于其平均流速的两倍，即
A2 A2 2 = [2 − 2 + ( ) − 1] 2 A1 A1 =
2 ρv2 A2
2 ρv2
2
(
A1
− 1) 2
A2 2 ς = ( − 1) A1
17
对于液流通过各种标准液压元件的局部损 失，一般可从产品技术规格中查到，但所 一般可从产品技术规格中查到， 查到的数据是在额定流量q 查到的数据是在额定流量 n时的压力损失 若实际通过流量与其不一样时， △pn，若实际通过流量与其不一样时，可 按下式计算， 按下式计算，即
300 ＜ λ= 0.3164/ Re0.25 Re ＜ 105 105 ≤ Re ≤ 108 λ= 0.308/ (0.824-lgRe) 2 λ=[ 1.14-2lg(△/ d +21.25/Re0.9)-2 λ= 0.11（△/ d ）0.25
14
（d/△）8/7 ＜ Re ＜597 △ （d/△）9/8 △ Re ＞597（d/△）9/8 （ △
15
例：截面突然扩大时的压力损失
由伯努力方程
2 p1 v12 p 2 v2 + = + + hr ρg 2 g ρg 2 g
∆pr = hr ρg A2 2 = p1 − p2 + [( ) − 1] A1 2
由动量方程
2 ρv2
p1 A1 + p0 ( A2 − A1 ) − p2 A2 = ρq(v2 − v1 )
umax＝2v
12
3．沿程压力损失
将
q=
π
4
f
d 2v
128µl ∆p f = q 4 πd vd µ = ρυ Re = 代入得
υ
2 2
∆p
64 l v l v = ρg = λ ρg Re d 2g d 2g
λ称为沿程阻力系数， 称为沿程阻力系数， λ 的理论值为 64/ Re， 水 在作层流流动时的实际 的理论值为64 / Re， 阻力系数和理论值是很接近的。 液压油在金属圆 阻力系数和理论值是很接近的 。 液压油 在金属圆 管中作层流流动时，常取λ 75/Re，在橡胶管中λ 管中作层流流动时，常取λ＝75/Re，在橡胶管中λ 80/Re。 ＝80/Re。
§1-4 管道流动
在液压传动中， 在液压传动中，能量损失主要表现为压力损失 ，压力损失 分为两类：沿程压力损失和局部压力损失。 分为两类：沿程压力损失和局部压力损失。 沿程压力损失： 沿程压力损失：油液沿等直径直管流动时因粘性摩擦所产生的 压力损失。 压力损失。 局部压力损失：油液流经局部障碍（如弯管、接头、 局部压力损失：油液流经局部障碍（如弯管、接头、管道截面 突然扩大或收缩） 由于液流的方向和速度的突然变化， 突然扩大或收缩 ） 时 ， 由于液流的方向和速度的突然变化 ， 在局部形成旋涡引起油液质点间， 在局部形成旋涡引起油液质点间 ， 以及质点与固体壁面间 相互碰撞和剧烈摩擦而产生的压力损失。 相互碰撞和剧烈摩擦而产生的压力损失。
• 压力效率低； 压力效率低； • 使油温上升，影响工作性能； 使油温上升，影响工作性能；
措施： 措施：
• • • • 尽量减小管道长度； 尽量减小管道长度； 尽量使管道内壁光滑； 尽量使管道内壁光滑； 选择适合的液压油粘度； 选择适合的液压油粘度； 增大通流面积，减小流速。 增大通流面积，减小流速。