圆锥曲线导学案
- 格式:doc
- 大小:573.50 KB
- 文档页数:22

《圆锥曲线(3):抛物线的基本知识》导学案(复习版)一. 知识全解(一)概念1・知识:1) __________________________________________ 定义:平面内与一个定点F 和一条定直线/( ___________________________________________ )的距离—的点的轨迹叫做抛物 线,点F 叫做抛物线的—,定直线/叫做抛物线的 _________ c (简称:一动两定距离相等)2) 定义式:设动点为M,定点为F,定直线为且动点到定点距离为|MF|,动点到定直线 的距离为d ,则由抛物线的定义可知抛物线上的点满足 _______________2 •全解:1) 平面内与一个定点F 和一条定直线/的距离相等的点的轨迹是抛物线,对吗?为什么? 2) 平面平面内与一个定点F 和一条定直线/(/不过F )的距离不等的点的轨迹一定不是抛 物线,对吗?为什么?3) 判断下列轨迹是不是抛物线,若是指出焦点和准线。
(二)标准方程1・知识:1)标准方程:(1) _____________________________________________________ 焦点在兀轴正半轴: (2) ________________________________________________ 焦点在y 轴正半轴: (3) ________________________________________________ 焦点在牙轴负半轴: (4) ________________________________________________ 焦点在y 轴负半轴: 2) 标准方程下的图形:(1) ________________________________________________ 焦点在兀轴正半轴: (2) ________________________________________________ 焦点在y 轴正半轴: (3) ________________________________________________ 焦点在牙轴负半轴: (4) ________________________________________________ 焦点在y 轴负半轴: 3) 焦点坐标:(1)标准方程为y 2=2px (p > 0) u>焦点坐标是 ___________ (2) _____________________________________________ 标准方程为x 2=-2py (p>0) <^>焦点坐标是 ___________________________________________(3) _____________________________________________ 标准方程为于=2卞(/7>0)0焦点坐标是 _____________________________________________ 。

圆锥曲线导学案一、自学准备与知识导学1、我们知道,用一个平面截一个圆锥面,当平面经过圆锥面的顶点时,可得到两条相交直线,当平面与圆锥面的轴垂直时,截得的图形是一个圆,试改变平面的位置,观察截得的图形的变化情况。
提出问题:用平面去截圆锥面能得到哪些曲线?2、建构数学(1)圆锥曲线的定义椭圆:平面内到两个定点1F ,2F 的距离的___等于常数(________)的点的轨迹叫做椭圆,两个定点1F ,2F 叫做椭圆的______,两焦点间的距离叫做椭圆的______。
对于第二种情形,平面与圆锥曲线的截线由两支曲线构成。
(类比椭圆的定义)双曲线:平面内到两定点1F ,2F 的距离的____________等于常数(小于12FF )的点的轨迹叫做双曲线,两个定点1F ,2F 叫做双曲线的______,两焦点间的距离叫做双曲线的______。
对于第三种情形,平面与圆锥曲线的截线是一条曲线构成。
抛物线:平面内到一个定点F 和一条定直线L (F 不在L 上)的___________的点轨迹叫做抛物线,定点叫做抛物线的_______,定直线L 叫做抛物线的______。
(2)圆锥曲线的定义式上面的三个结论我们都可以用数学表达式来体现:设平面内的动点为M 。
椭圆:动点M 满足的式子:双曲线:动点M 满足的式子:抛物线:动点M 满足的式子:我们可利用上面的三条关系式来判断动点M 的轨迹是什么!二、学习交流与问题探讨例1、试用适当的方法作出以两个定点1F ,2F 为焦点的一个椭圆。
思考:在椭圆的定义中,如果这个常数小于或等于点1F 2F ,动点的轨迹又如何呢? 例2、已知三角形ABC 中,B (-3,0),C (3,0),且AB ,BC ,AC 成等差数列。
(1)求证:点A 在一个椭圆上运动; (2)写出这个椭圆的焦点坐标。
略解:由AB ,BC ,AC 成等差数列,可得2BC=AB+AC,即AB+AC=12>BC,由椭圆的 定义可得点A 在一个椭圆上运动,且以B 、C 为焦点。

§ 1.1.1 椭圆及其标准方程 (第一课时 ) 编辑:唐灿华班级姓名学习目标1.理解并掌握椭圆的定义,焦距.2.掌握椭圆的标准方程及其捧导方法提示与建议重视圆锥曲线的定义在解题中的作用.【互动探究】 自主探究☆1. ___________________________ 叫做椭圆, 这两个定点叫做, 叫做圆的焦距. ☆2. 焦点在 x 轴上的椭圆的标准方程是 . ☆3. 焦点在 y轴上的椭圆的标准方程是 .☆ 4. 在椭圆的标准方程中,分母的大小反映了焦点所在 的坐标轴.并且 a2、 b2、 c 2之间的关系是.剖例探法 ★讲解点一 椭圆定义的应用审核:黎业建座号.【规律技巧总结】由于两小题都没有具体指明椭圆的焦点在哪一个坐标轴上, 所以应考虑两种形式的标准方程,可用待定系数法求椭圆方程.【自我测评】☆ 1. a6, c 1的椭圆标准方程是 ( ) A . x 2y 2 1 B . y 2x 2 1 36 35 36 35C . x 2y 2 1D .以上都不对365☆2.已知动圆P 过定点 A(3,0) ,并且在定圆B : (x 3)2y264的内部与定圆相切,则动圆的圆心P的轨迹是 ( )A .线段B.直线C .圆D .椭圆x2y2☆☆ 例题 1椭圆1的焦点为 F 1 和 F 2 ,点 P 在椭圆.如16 9果F 1 PF 2 60 ,求 F 1PF 2的面积【思维切入】 利用椭圆的定义和余弦定理求面积★讲解点二椭圆标准方程的求法☆例题 2 根据下列条件求椭圆标准方程:(1) 已知 P 点在以坐标轴为对称轴的椭圆上, 点 P 到两焦点的距离分别为 4 5和2 5,过P 作坐标轴的垂线恰好过椭圆的一个焦3 3点.(2) 经过两点 A(0, 2)1 和B( , 3).2☆ 3.已知椭圆x2y225 1 上一点 P 到椭圆一个焦点的距离为163,则 P 到另一个焦点的距离为( )A .2B .3C .5D .7☆4. (陕西卷·文 7 题 ) “m n 0 ” 是 “ 方 程mx 2 ny21y轴上的椭圆”的”表示焦点在( )A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件x2y21表示焦点在y 轴上的椭☆ 5. 若方程10 圆,则k 5k 实数 k 的取值范围是 __________ .☆ ☆ 6 . 椭 圆 ax 2by 2ab 0(a b0) 的焦点坐标是__________ .【拓展迁移】 思维提升☆☆ 7. 求经过点 ( 一 2, 3) 且与椭圆 9x 24 y 236 有共同焦点的椭圆方程 .§ 1.1.2 椭圆及其标准方程(第二课时)编辑:唐灿华审核:黎业建班级姓名 座号.学习目标能用直接法、定义法、相关点法等方法求椭圆的轨迹方程.提示与建议加强运用数形结合的思想方法, 提高分析问题、 解决问题的能力.【互动探究】 自主探究☆ 1.用待定系数法求椭圆的标准方程步骤如下: ①作判断:依据条件判断椭圆的焦点存 x 轴上还是在 y 轴上,还是两个坐标轴上都有可能;②设方程:依据上述判断设方程为 __________ 或__________ ;③寻关系: 依据已知条件, 建立关于 a,b, c 或 m, n 的方程 组;④得方程:解方程则,代人所设方程即为所求.剖例探法 ★讲解点一定义法求椭圆轨迹方程☆ 例 2 已知圆 A : ( x 2) 2y236 ,圆 A 内一定点B(2, 0) ,圆 P 过 B 点且与圆 A 内切,求圆心 P 的轨迹方程.★讲解点二 相关点法求椭圆轨迹方程☆ 例 3 已知圆x 2y 2 9 ,从这个圆上任意一点 P 向 x轴作垂线段 PP / ,点M 在PP / 上,并且 PM 2MP / ,求点M 的轨迹。

圆锥曲线------ 极坐标系与参数方程【目标】:1、掌握点的极坐标与直角坐标的互化;2、掌握曲线的极坐标方程与直角坐标方程的互化;3、会把极坐标系的问题转化为直角坐标系的问题解决;4、掌握曲线的参数方程与普通(直角坐标)方程的互化;5、会参数方程解决曲线的交点与最值问题。
坐标系一、知识要点1. 对于极坐标系内任意一点M ,用ρ表示线段OM 的长度,用θ表示从Ox 到OM 的角度,则ρ叫做点M 的 ,θ叫做点M 的 ,点M 的极坐标是 。
2. 极坐标与直角坐标的互化公式:x = ,y = ,2ρ = , θtan = 。
3. 特殊的圆的极坐标方程: r,2cos ,2sin ,cos sin a a a b ρρθρθρθθ====+4. 特殊的直线的极坐标方程:sin ,cos ,(R),a a ρθρθθαρ===∈ 二、例题与练习1. 点M 的直角坐标是 (1-,则M 点的极坐标为( )2.(2,).(2,).(2,).(2,2),()3333A B C D k k Z πππππ-+∈2. 曲线的极坐标方程θρsin 4=化为直角坐标方程为 .3. 在极坐标系中,过点4π⎛⎫⎪⎝⎭作圆4sin ρθ=的切线,则切线的极坐标方程是 .4. 在极坐标系中,已知直线过点(1,0),且其向上的方向与极轴的正方向所成的最小正角为3π,则直线的极坐标方程为______________.5. 在极坐标系中,圆C 的极坐标方程是π4cos 6ρθ⎛⎫=+ ⎪⎝⎭。
现以极点为原点,以极轴为x 轴的正半轴建立直角坐标系,则圆C 的半径是 ,圆心的直角坐标是 。
6.极坐标内曲线2sin ρθ=的中心O 与点D ()1,π的距离为 .7. 在极坐标系中,点A (1,)4π到直线sin 2ρθ=-的距离是__ _ _.8. 已知圆的极坐标方程2cos ρθ=,直线的极坐标方程为cos 2sin 70ρθρθ-+=,则圆心到直线距离为 .9. 极坐标系中,曲线4sin ρθ=-和cos 1ρθ=相交于点,A B ,则AB = ;10. 在极坐标系中,直线π3θ=(ρ∈R )与圆4cos ρθ=+θ交于A 、B 两点,则AB = .11. 设M、N分别是曲线2sin 0ρθ+=和s ()4in πρθ+=上的动点,则M、N的最小距离是12. 在极坐标系中,圆2cos ρθ=的圆心的极坐标是 ,它与方程π4θ=(0ρ>)所表示的图形的交点的极坐标是 .13. 已知曲线21,C C 的极坐标方程分别为θρθρcos 4,3cos ==(20,0πθρ<≤≥),则曲线1C 与2C 交点的极坐标为__ ___.14. 极坐标系下,直线2)4cos(=-πθρ 与圆2=ρ的公共点个数是_____.15. 在极坐标系中,过点π4,2A ⎛⎫- ⎪⎝⎭引圆4sin ρθ=的一条切线,则切线长为 .参数方程一、知识要点1. 在平面直角坐标系中,如果曲线上任意一点的坐标x,y 都是某个变数t 的函数 x f (t),y g(t),=⎧⎨=⎩,并且对于t 的每一个允许值,由这个方程所确定的点M(x,y)都在这条曲线上,那么这个方程就叫做这条曲线的参数方程,联系变数x,y 的变数t 叫做参变数,简称参数。

的直线方程 .复习2:方程22(3)(1)4x y -++= 表示以 为圆心, 为半径的 .二、新课导学※ 学习探究取一条定长的细绳,把它的两端都固定在图板的同一个点处,套上铅笔,拉紧绳子,移动笔尖,这时笔尖画出的轨迹是一个 .如果把细绳的两端拉开一段距离,分别固定在图板的两个点处,套上铅笔,拉紧绳子,移动笔尖,画出的轨迹是什么曲线?思考:移动的笔尖(动点)满足的几何条件是什么?经过观察后思考:在移动笔尖的过程中,细绳的 保持不变,即笔尖 等于常数.新知1: 我们把平面内与两个定点12,F F 的距离之和等于常数(大于12F F )的点的轨迹叫做椭圆,这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距 .反思:若将常数记为2a ,为什么122a F F >?当122a F F =时,其轨迹为 ;当122a F F <时,其轨迹为 .试试:已知1(4,0)F -,2(4,0)F ,到1F ,2F 两点的距离之和等于8的点的轨迹是 .小结:应用椭圆的定义注意两点:①分清动点和定点; ②看是否满足常数122a F F >.新知2:焦点在x 轴上的椭圆的标准方程 ()222210x y a b a b+=>> 其中222b a c =-若焦点在y 轴上,两个焦点坐标 ,则椭圆的标准方程是 .※ 典型例题例1 写出适合下列条件的椭圆的标准方程: ⑴4,1a b ==,焦点在x 轴上;⑵4,a c ==y 轴上;⑶10,a b c +==.变式:方程214x y m+=表示焦点在x 轴上的椭圆,则实数m 的范围 .小结:椭圆标准方程中:222a b c =+ ;a b > .例2 已知椭圆两个焦点的坐标分别是()2,0-,(2,0),并且经过点53,22⎛⎫- ⎪⎝⎭,求它的标准方程 .变式:椭圆过点 ()2,0-,(2,0),(0,3),求它的标准方程.小结:由椭圆的定义出发,得椭圆标准方程 .练习1.平面内一动点M 到两定点1F 、2F 距离之和为常数2a ,则点M 的轨迹为( ).A .椭圆B .圆C .无轨迹D .椭圆或线段或无轨迹2.如果方程222x ky +=表示焦点在y 轴上的椭圆,那么实数k 的取值范围是( ).A .(0,)+∞B .(0,2)C .(1,)+∞D .(0,1)3.如果椭圆22110036x y +=上一点P 到焦点1F 的距离等于6,那么点P 到另一个焦点2F 的距离是( ).A .4B .14C .12D .84.椭圆两焦点间的距离为16,且椭圆上某一点到两焦点的距离分别等于9和15,则椭圆的标准方程是 .5.如果点(,)M x y 在运动过程中,10=,点M 的轨迹是 ,它的方程是 .课后作业1. 写出适合下列条件的椭圆的标准方程:⑴焦点在x 轴上,焦距等于4,并且经过点(3,P -; ⑵焦点坐标分别为()()0,4,0,4-,5a =; ⑶10,4a c a c +=-=.2. 椭圆2214x y n +=的焦距为2,求n 的值.。

<圆锥曲线的定义、标准方程、几何性质》导学案【学情分析】学生已经学习过了圆锥曲线的有关知识,对相关的内容有一个基本的掌握。
【教学目标】通过复习进一步加深对圆锥曲线定义的理解;较熟练地掌握利用求待定系数法求标准方程;能灵活处理圆锥曲线的几何性质。
【教学重难点】重点:椭圆、双曲线、抛物线的标准方程和几何性质及其应用;难点:椭圆、双曲线的离心率的求法。
【教学过程】环节一、学1.椭圆的概念在平面内的动点M与两定点F1、F2的距离之_____等于常数(_____|F1F2|)的点的轨迹叫做椭圆.集合P={M||MF1|+|MF2|=2a},|F1F2|=2c,其中a、c为常数且a>0,c>0:(1)若a>c,则集合P为_______;(2)若a=c,则集合P为_______;(3)若a<c,则集合P 为_______.2.双曲线的概念平面内动点M与两个定点F1、F2的距离之_____________为常数(_____|F1F2|),则点P的轨迹叫双曲线.集合P={M|||MF1|-|MF2||=2a},|F1F2|=2c,其中a、c为常数且a>0,c>0:(1)若a>c,则集合P为_______;(2)若a=c,则集合P为_______;(3)若a<c,则集合P 为_______.3.抛物线的概念平面内动点M与一个定点F和一条定直线l(F___l)的距离_______的点的轨迹叫做抛物线. 时,动点M的轨迹是。
若F l4.椭圆的标准方程和几何性质5.双曲线的标准方程和几何性质6例1. AB 为过椭圆x 2a 2+y 2b2=1中心的弦,F (c,0)为它的焦点,则△F AB 的最大面积为 ( )A .b 2B .abC .acD .bc例2. 已知双曲线E 的中心为原点,F (3,0)是E 的焦点,过F 的直线l 与E 相交于A ,B 两点,且AB 的中点为N (-12,-15),则E 的方程为 ( ) A.x 23-y 26=1B.x 24-y 25=1 C.x 26-y 23=1 D.x 25-y 24=1例3. 过抛物线y 2=2px (p >0)的焦点F 且倾斜角为60°的直线与抛物线在第一、四象限分别交于A 、B 两点,则|AF ||BF |等于 ( )环节三、练1. 设M (x 0,y 0)为抛物线C :x 2=8y 上一点,F 为抛物线C 的焦点,以F 为圆心、|FM |为半径的圆和抛物线C 的准线相交,则y 0的取值范围是 ( ) A .(0,2)B .[0,2]C .(2,+∞)D .[2,+∞)2.已知抛物线y =-x 2+3上存在关于直线x +y =0对称的相异两点A 、B ,则|AB |等于 ( )A .3B .4C .3 2D .4 23. 已知椭圆x 24+y 2=1的两个焦点为F 1、F 2,过F 1作垂直于x 轴的直线与椭圆相交,一个交点为P ,则|PF 2|=______.环节四、测1. 直线y =kx +2与抛物线y 2=8x 有且只有一个公共点,则k 的值为 ( )A .1B .1或3C .0D .1或02.已知过抛物线y 2=2px (p >0)的焦点F 的直线x -my +m =0与抛物线交于A 、B 两点, 且△OAB (O 为坐标原点)的面积为22, 则m 6+m 4的值是 ( )A .1 B. 2C .2D .4.3. 设抛物线x 2=4y 的焦点为F ,经过点P (1,4)的直线l 与抛物线相交于A 、B 两点,且点P恰为AB 的中点,则|AF →|+|BF →|=________.4.直线y =kx -2与抛物线y 2=8x 交于不同两点A 、B ,且AB 的中点横坐标为2,则k 的值是________.5.直线y =kx +1与椭圆x 25+y 2m=1恒有公共点,则m 的取值范围是__________.6.已知双曲线x 2a 2-y 2b 2=1 (a >1,b >0)的焦距为2c ,离心率为e ,若点(-1,0)与(1,0)到直线x a -yb=1的距离之和s ≥45c ,则e 的取值范围是__________.7.若过抛物线y 2=2px (p >0)的焦点F 的直线l 依次交抛物线及其准线于点A 、B 、C ,若|BC |=2|BF |,且|AF |=3,则抛物线的方程为____________ 8.在平面直角坐标系xOy 中,已知双曲线C 1:2x 2-y 2=1.(1)过C 1的左顶点引C 1的一条渐近线的平行线,求该直线与另一条渐近线及x 轴围成的三角形的面积.(2)设斜率为1的直线l 交C 1于P 、Q 两点.若l 与圆x 2+y 2=1相切,求证:OP ⊥OQ . (3)设椭圆C 2:4x 2+y 2=1.若M 、N 分别是C 1、C 2上的动点,且OM ⊥ON ,求证:O 到直线MN 的距离是定值.9. 椭圆x 2a 2+y 2b2=1 (a >b >0)与直线x +y -1=0相交于P 、Q 两点,且OP ⊥OQ (O 为原点).(1)求证:1a 2+1b 2等于定值;(2)若椭圆的离心率e ∈⎣⎡⎦⎤33,22,求椭圆长轴长的取值范围.环节五、评【教学反思】。

圆锥曲线与方程复习导学案一、我的知识我完善1、课标要求(1)了解圆锥曲线的实际背景,感受圆锥曲线在刻画现实世界和解决实际问题中的作用;(2)经历从具体情境中抽象出椭圆、抛物线模型的过程,掌握它们的定义、标准方程、几何图形及简单性质;(3)了解双曲线的定义、几何图形和标准方程,知道双曲线的有关性质。
2、命题走向本讲内容是圆锥曲线的基础内容,也是高考重点考查的内容,从近十年高考试题看,选择题、填空题和解答题都涉及到,所占比重也比较稳定,难度上易、中、难三档题都有,客观题主要考察圆锥曲线的基本概念、标准方程及几何性质等基础知识,而解答题则主要考查直线与圆锥曲线的位置关系和处理综合性问题的基本技能、基本方法。
3、根据以下知识网络请你说说各板块你所学到的东西二、我的例题我探究题型一圆锥曲线定义的应用圆锥曲线的定义是相应标准方程和几何性质的“根”,对于圆锥曲线的有关问题,要有运用定义去解题的意识,“归根”是一种重要的解题策略。
例1 若点)1,2(P ,1F 、2F 是椭圆171622=+y x 的左、右焦点,点A 是椭圆上一个动点,求||||2AF AP +的最值.----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------变式训练1已知F 是双曲线112422=-y x 的左焦点,点)4,1(A ,P 是双曲线右支上的动点,则||||PA PF +的最小值为---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- 变式训练2 已知点P 是抛物线x y 22=上的一个动点,又点)2,0(M ,求点P 到点M 的距离与点P 到该抛物线准线的距离之和的最小值.--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- 小结:对于椭圆和双曲线常把曲线上的点到焦点的距离转化为到另一个焦点的距离,对于抛物线常把到焦点的距离和到准线的距离进行转化,再利用数学结合的思想去解决有关最值问题题型二 圆锥曲线性质的问题有关圆锥曲线的焦点、离心率、渐近线等几何性质是历年来高考中必考的,考试只要掌握基本公式和概念,利用数学结合思想基本可以顺利解决。
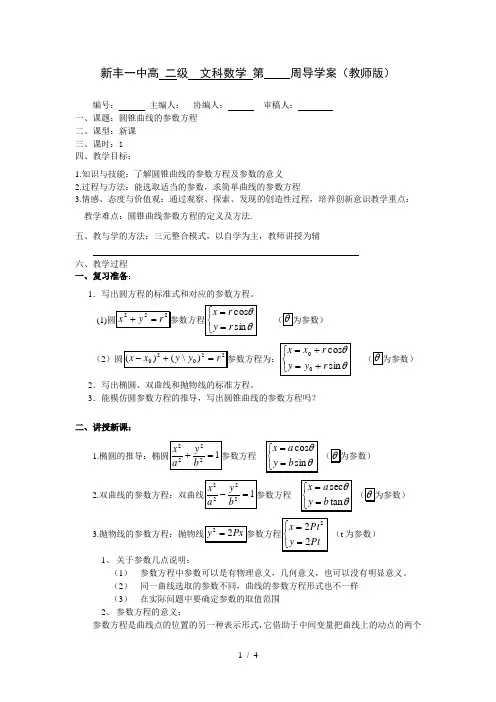
新丰一中高二级文科数学第周导学案(教师版)编号:主编人:协编人:审稿人:一、课题:圆锥曲线的参数方程二、课型:新课三、课时:1四、教学目标:1.知识与技能:了解圆锥曲线的参数方程及参数的意义2.过程与方法:能选取适当的参数,求简单曲线的参数方程3.情感、态度与价值观:通过观察、探索、发现的创造性过程,培养创新意识教学重点:教学难点:圆锥曲线参数方程的定义及方法.五、教与学的方法:三元整合模式,以自学为主,教师讲授为辅六、教学过程一、复习准备:1.写出圆方程的标准式和对应的参数方程。
(1)(22.写出椭圆、双曲线和抛物线的标准方程。
3.能模仿圆参数方程的推导,写出圆锥曲线的参数方程吗?二、讲授新课:1.2.3.(t为参数)1、关于参数几点说明:(1)参数方程中参数可以是有物理意义,几何意义,也可以没有明显意义。
(2)同一曲线选取的参数不同,曲线的参数方程形式也不一样(3)在实际问题中要确定参数的取值范围2、参数方程的意义:参数方程是曲线点的位置的另一种表示形式,它借助于中间变量把曲线上的动点的两个坐标间接地联系起来,参数方程与变通方程同等地描述,了解曲线,参数方程实际上是M的横坐标和纵坐标。
3、参数方程求法(1)建立直角坐标系,设曲线上任一点P(2)选取适当的参数(3)根据已知条件和图形的几何性质,物理意义,建立点P坐标与参数的函数式(4)证明这个参数方程就是所由于的曲线的方程4、关于参数方程中参数的选取选取参数的原则是曲线上任一点坐标当参数的关系比较明显关系相对简单。
或选取有向线段的数量、长度、直线的倾斜斜角、斜率等。
二、典型例题:例1(1)求子弹弹道曲线的参数方程(不计空气阻力)(22秒时,①求炮弹高度②求出炮弹的射程例2.求椭圆的参数方程(见教材P.40)变式训练1.求(1P的坐标(2)直线OP的倾斜角变式训练2 A点椭圆长轴一个端点,若椭圆上存在一点P,使∠OPA=90°,其中O为三、巩固与练习填空题1.(广东卷理15)在极坐标系(ρ,θ)(0 ≤ θ<2π)中,曲线ρ与的交点的极坐标为______。

课题:2.1.1椭圆及其标准方程(第1课时)【学习目标】1、能从具体情境中抽象出椭圆的模型;2、理解椭圆的定义,会求椭圆的标准方程. 【学习重点】1、理解椭圆的定义和标准方程;2、认识椭圆标准方程的特征. 【学法指导】1、带着预习案中问题导学中的问题自主设计预习提纲,通读教材内容,对概念、关键词进行梳理,作好必要的标注和笔记。
2、认真完成基础知识梳理,在“我的疑惑”处填上自己不懂的知识点,在“我的收获”处填写自己对本课自主学习的知识及方法收获。
3、熟记基础知识梳理中的重点知识。
【自主学习】一、问题导学在椭圆的标准方程中,2a 和2b 能相等吗? 二、知识梳理1.椭圆的定义:我们把 与两个定点1F ,2F 的 等于常数( )的点的轨迹叫做椭圆.这两个定点叫做椭圆的 ,两 间的距离叫做椭圆的 .用数学符号可以把定义表示为 . 2.椭圆的标准方程:(1)当 在x 轴上时,标准方程为 ( ). 当 在y 轴上时,标准方程为 ( ).(2)参数,,a b c 之间的关系是:①等量关系 ;②不等关系 三、预习自测1.已知()()3,0,3,0A B -,动点M 分别满足下列关系,问:M 的轨迹是否存在,若存在,是什么曲线? (1)10MA MB +=;(2)6MA MB +=;(3)4MA MB +=.2.已知椭圆的方程如下,写出,,a b c 的值及焦点坐标:(1)221259x y +=; (2)2211625x y +=; (3)2222x y +=. 3.写出适合下列条件的椭圆的标准方程:(1)4,1a b ==,焦点在x 轴上;(2)4,a c ==y 轴上;(3)10,6a c ==【合作探究】判断下列方程是否表示椭圆,若是,写出,,a b c 及焦点坐标(1)22144x y +=;(2)22143x y +=;(3)22134x y +=;(4)22143x y -=;(5)22231x y +=.【拓展延伸】已知()()121,0,1,0F F -是椭圆的两个焦点,并且经过点31,2A ⎛⎫- ⎪⎝⎭,求它的标准方程.【当堂检测】1.若12,F F 分别是椭圆223530x y +=的左、右焦点,M 是椭圆上的任一点,且12MF =,则2MF = .2.已知椭圆221kx y +=的焦点在x 轴上,则k 的取值范围是 . 3.写出适合下列条件的椭圆的标准方程:(1)焦点在x 轴上,焦距等于4,并且经过点(0,P ;(2)9,1a c a c +=-=.课题:2.1.1椭圆及其标准方程(第2课时)【学习目标】1、理解椭圆定义,掌握椭圆的标准方程;2、会求与椭圆有关的轨迹问题。

§2.1.1 曲线与方程(1)1.理解曲线的方程、方程的曲线;2.求曲线的方程.3436,找出疑惑之处)复习1:画出函数22y x=(12)x-≤≤的图象.复习2:画出两坐标轴所成的角在第一、三象限的平分线,并写出其方程.二、新课导学※学习探究探究任务一:到两坐标轴距离相等的点的集合是什么?写出它的方程.问题:能否写成y x=,为什么?新知:曲线与方程的关系:一般地,在坐标平面内的一条曲线C与一个二元方程(,)0F x y=之间,如果具有以下两个关系:1.曲线C上的点的坐标,都是的解;2.以方程(,)0F x y=的解为坐标的点,都是的点,那么,方程(,)0F x y=叫做这条曲线C的方程;曲线C叫做这个方程(,)0F x y=的曲线.注意:1︒如果……,那么……;2︒“点”与“解”的两个关系,缺一不可;3︒曲线的方程和方程的曲线是同一个概念,相对不同角度的两种说法;4︒曲线与方程的这种对应关系,是通过坐标平面建立的.试试:1.点(1,)P a在曲线2250x xy y+-=上,则a=___ .2.曲线220x xy by+-=上有点(1,2)Q,则b= .新知:根据已知条件,求出表示曲线的方程.※典型例题例 1 证明与两条坐标轴的距离的积是常数(0)k k>的点的轨迹方程式是xy k=±.变式:到x轴距离等于5的点所组成的曲线的方程是50y-=吗?例2设,A B两点的坐标分别是(1,1)--,(3,7),求线段AB的垂直平分线的方程.变式:已知等腰三角形三个顶点的坐标分别是(0,3)A,(2,0)B-,(2,0)C.中线AO(O为原点)所在直线的方程是0x=吗?为什么?反思:BC边的中线的方程是0x=吗?小结:求曲线的方程的步骤:①建立适当的坐标系,用(,)M x y表示曲线上的任意一点的坐标;②写出适合条件P的点M的集合{|()}P M p M=;③用坐标表示条件P,列出方程(,)0f x y=;④将方程(,)0f x y=化为最简形式;⑤说明以化简后的方程的解为坐标的点都在曲线上.※动手试试练1.下列方程的曲线分别是什么?(1)2xyx=(2)222xyx x-=-(3) log a xy a=练2.离原点距离为2的点的轨迹是什么?它的方程是什么?为什么?三、总结提升※学习小结1.曲线的方程、方程的曲线;2.求曲线的方程的步骤:①建系,设点;②写出点的集合;③列出方程;④化简方程;⑤验证.※知识拓展求轨迹方程的常用方法有:直接法,定义法,待定系数法,参数法,相关点法(代入法),交轨法等.※自我评价你完成本节导学案的情况为().A. 很好B. 较好C. 一般D. 较差※当堂检测(时量:5分钟满分:10分)计分:1. 与曲线y x=相同的曲线方程是().A.2xyx=B.y=C.y=D.2log2xy=2.直角坐标系中,已知两点(3,1)A,(1,3)B-,若点C满足OCu u u r=αOAu u u r+βOBu u u r,其中α,β∈R,α+β=1,则点C的轨迹为( ) .A.射线B.直线C.圆D.线段3.(1,0)A,(0,1)B,线段AB的方程是().A.10x y-+=B.10x y-+=(01)x≤≤C.10x y+-=D.10x y-+=(01)x≤≤4.已知方程222ax by+=的曲线经过点5(0,)3A和点(1,1)B,则a= ,b= .5.已知两定点(1,0)A-,(2,0)B,动点p满足12PAPB=,则点p的轨迹方程是.1.点(1,2)A-,(2,3)B-,(3,10)C是否在方程2210x xy y-++=表示的曲线上?为什么?2 求和点(0,0)O,(,0)A c距离的平方差为常数c的点的轨迹方程.§2.1.2 曲线与方程(2)1. 求曲线的方程;2. 通过曲线的方程,研究曲线的性质.3637,找出疑惑之处)复习1:已知曲线C 的方程为 22y x = ,曲线C 上有点(1,2)A ,A 的坐标是不是22y x = 的解?点(0.5,)t 在曲线C 上,则t =___ .复习2:曲线(包括直线)与其所对应的方程(,)0f x y =之间有哪些关系?二、新课导学 ※ 学习探究 引入:圆心C 的坐标为(6,0),半径为4r =,求此圆的方程.问题:此圆有一半埋在地下,求其在地表面的部分的方程.探究:若4AB =,如何建立坐标系求AB 的垂直平分线的方程.※ 典型例题例1 有一曲线,曲线上的每一点到x 轴的距离等于这点到(0,3)A 的距离的2倍,试求曲线的方程.变式:现有一曲线在x 轴的下方,曲线上的每一点到x 轴的距离减去这点到点(0,2)A ,的距离的差是2,求曲线的方程.小结:点(,)P a b 到x 轴的距离是 ;点(,)P a b 到y 轴的距离是 ; 点(1,)P b 到直线10x y +-=的距离是 .例2已知一条直线l 和它上方的一个点F ,点F 到l 的距离是2,一条曲线也在l 的上方,它上面的每一点到F 的距离减去到l 的距离的差都是2,建立适当的坐标系,求这条曲线的方程.※动手试试练1.有一曲线,曲线上的每一点到x轴的距离等于这点到直线10x y+-=的距离的2倍,试求曲线的方程.练2. 曲线上的任意一点到(3,0)A-,(3,0)B两点距离的平方和为常数26,求曲线的方程.三、总结提升※学习小结1. 求曲线的方程;2. 通过曲线的方程,研究曲线的性质.※知识拓展圆锥曲线的统一定义:到定点的距离与到定直线的距离之比为常数e 的点的轨迹是圆锥曲线.01e<<:椭圆;1e=:抛物线;1e>:双曲线.※自我评价你完成本节导学案的情况为().A. 很好B. 较好C. 一般D. 较差※当堂检测(时量:5分钟满分:10分)计分:1.方程[]2(3412)log(2)30x y x y--+-=的曲线经过点(0,3)A-,(0,4)B,(4,0)C,57(,)34D-中的().A.0个B.1个C.2个D.3个2.已知(1,0)A,(1,0)B-,动点满足2MA MB-=,则点M的轨迹方程是(). A.0(11)y x=-≤≤B.0(1)y x=≥C.0(1)y x=≤-D.0(1)y x=≥3.曲线y=与曲线0y x+=的交点个数一定是().A.0个B.2个C.4个D.3个4.若定点(1,2)A与动点(,)P x y满足4OP OA•=vv,则点P的轨迹方程是.5.由方程111x y-+-=确定的曲线所围成的图形的面积是.1.以O为圆心,2为半径,上半圆弧的方程是什么?在第二象限的圆弧的方程是什么?2.已知点C的坐标是(2,2),过点C的直线CA与x 轴交于点A,过点C且与直线CA垂直的直线CB与y轴交于点B.设点M是线段AB的中点,求点M 的轨迹方程.§2.2.1椭圆及其标准方程(1)1.从具体情境中抽象出椭圆的模型;2.掌握椭圆的定义; 3.掌握椭圆的标准方程.3840,文P 32~ P 34找出疑惑之处) 复习1:过两点(0,1),(2,0)的直线方程 . 复习2:方程22(3)(1)4x y -++= 表示以 为圆心, 为半径的 .二、新课导学※ 学习探究取一条定长的细绳, 把它的两端都固定在图板的同一个点处,套上铅笔,拉紧绳子,移动笔尖,这时笔尖画出的轨迹是一个 . 如果把细绳的两端拉开一段距离,分别固定在图板的两个点处,套上铅笔,拉紧绳子,移动笔尖,画出的轨迹是什么曲线?思考:移动的笔尖(动点)满足的几何条件是什么?经过观察后思考:在移动笔尖的过程中,细绳的 保持不变,即笔尖 等于常数.新知1: 我们把平面内与两个定点12,F F 的距离之和等于常数(大于12F F )的点的轨迹叫做椭圆,这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距 .反思:若将常数记为2a ,为什么122a F F >? 当122a F F =时,其轨迹为 ; 当122a F F <时,其轨迹为 .试试: 已知1(4,0)F -,2(4,0)F ,到1F ,2F 两点的距离之和等于8的点的轨迹是 .小结:应用椭圆的定义注意两点:①分清动点和定点;②看是否满足常数2a F F >.新知2:焦点在x 轴上的椭圆的标准方程 ()222210x y a b a b +=>> 其中222b a c =-若焦点在y 轴上,两个焦点坐标 ,则椭圆的标准方程是 . ※ 典型例题例1 写出适合下列条件的椭圆的标准方程: ⑴4,1a b ==,焦点在x 轴上;⑵4,ac =y 轴上; ⑶10,a b c +==.变式:方程214x ym +=表示焦点在x 轴上的椭圆,则实数m 的范围 .小结:椭圆标准方程中:222a b c =+ ;a b > .例2 已知椭圆两个焦点的坐标分别是()2,0-,(2,0),并且经过点53,22⎛⎫- ⎪⎝⎭,求它的标准方程 .变式:椭圆过点 ()2,0-,(2,0),(0,3),求它的标准方程.小结:由椭圆的定义出发,得椭圆标准方程 .※ 动手试试练 1. 已知ABC ∆的顶点B 、C 在椭圆2213x y +=上,顶点A 是椭圆的一个焦点,且椭圆的另外一个焦点在BC 边上,则ABC ∆的周长是( ). A . B .6C .D .12练2 .方程219x ym-=表示焦点在y 轴上的椭圆,求实数m 的范围.三、总结提升 ※ 学习小结 1. 椭圆的定义: 2. 椭圆的标准方程:※ 知识拓展1997年初,中国科学院紫金山天文台发布了一条消息,从1997年2月中旬起,海尔·波普彗星将逐渐接近地球,过4月以后,又将渐渐离去,并预测3000年后,它还将光临地球上空 1997年2月至3月间,许多人目睹了这一天文现象出彗星出现的准确时间呢?原来,海尔·波普彗星运行的轨道是一个椭圆,通过观察它运行中的一些有关数据,可以推算出它的运行轨道的方程,从而算※ 自我评价 你完成本节导学案的情况为( ). A. 很好 B. 较好 C. 一般 D. 较差※ 当堂检测(时量:5分钟 满分:10分)计分: 1.平面内一动点M 到两定点1F 、2F 距离之和为常数2a ,则点M 的轨迹为( ). A .椭圆 B .圆C .无轨迹D .椭圆或线段或无轨迹 2.如果方程222x ky +=表示焦点在y 轴上的椭圆,那么实数k 的取值范围是( ). A .(0,)+∞ B .(0,2) C .(1,)+∞ D .(0,1)3.如果椭圆22110036x y +=上一点P 到焦点1F 的距离等于6,那么点P 到另一个焦点2F 的距离是( ). A .4 B .14 C .12 D .84.椭圆两焦点间的距离为16,且椭圆上某一点到两焦点的距离分别等于9和15,则椭圆的标准方程 是.5.如果点(,)M x y 在运动过程中,总满足关系式10=,点M 的轨迹是 ,它的方程是 .1. 写出适合下列条件的椭圆的标准方程:⑴焦点在x 轴上,焦距等于4,并且经过点(3,P -;⑵焦点坐标分别为()()0,4,0,4-,5a =; ⑶10,4a c a c +=-=.2. 椭圆2214x y n+=的焦距为2,求n 的值.§2.2.1 椭圆及其标准方程(2)1.掌握点的轨迹的求法;2.进一步掌握椭圆的定义及标准方程.4142,文P 34~ P 36找出疑惑之处)复习1:椭圆上221259x y+=一点P 到椭圆的左焦点1F 的距离为3,则P 到椭圆右焦点2F 的距离 是 .复习2:在椭圆的标准方程中,6a =,b =则椭圆的标准方程是 .二、新课导学 ※ 学习探究问题:圆22650x y x +++=的圆心和半径分别是什么?问题:圆上的所有点到 (圆心)的距离都等于 (半径) ;反之,到点(3,0)-的距离等于2的所有点都在 圆 上.※ 典型例题例1在圆224x y +=上任取一点P ,过点P 作x 轴的垂线段PD ,D 为垂足.当点P 在圆上运动时,线段PD 的中点M 的轨迹是什么?变式: 若点M 在DP 的延长线上,且32DM DP =,小结:椭圆与圆的关系:圆上每一点的横(纵)坐标不变,而纵(横)坐标伸长或缩短就可得到椭圆.例2设点,A B 的坐标分别为()()5,0,5,0-,.直线,AM BM 相交于点M ,且它们的斜率之积是49-,求点M 的轨迹方程 .变式:点,A B 的坐标是()()1,0,1,0-,直线,AM BM 相交于点M ,且直线AM 的斜率与直线BM 的斜率的商是2,点M 的轨迹是什么?※ 动手试试 练1.求到定点()2,0A 与到定直线8x=的距离之比练2.一动圆与圆22650x y x +++=外切,同时与圆226910x y x +--=内切,求动圆圆心的轨迹方程式,并说明它是什么曲线.三、总结提升 ※ 学习小结1. ①注意求哪个点的轨迹,设哪个点的坐标,然后找出含有点相关等式;②相关点法:寻求点M 的坐标,x y 与中间00,x y 的关系,然后消去00,x y ,得到点M 的轨迹方程.※ 知识拓展椭圆的第二定义:到定点F 与到定直线l 的距离的比是常数e (01)e <<的点的轨迹. 定点F 是椭圆的焦点; 定直线l 是椭圆的准线; 常数e 是椭圆的离心率.※ 自我评价 你完成本节导学案的情况为( ). A. 很好 B. 较好 C. 一般 D. 较差※ 当堂检测(时量:5分钟 满分:10分)计分: 22αα曲线是椭圆,则α在( ).A .第一象限B .第二象限C .第三象限D .第四象限 2.若ABC ∆的个顶点坐标(4,0)A -、(4,0)B ,ABC ∆的周长为18,则顶点C 的轨迹方程为( ).A .221259x y +=B .221259y x += (0)y ≠C .221169x y +=(0)y ≠D .221259x y +=(0)y ≠3.设定点1(0,2)F - ,2(0,2)F ,动点P 满足条件124(0)PF PF m m m+=+>,则点P 的轨迹是( ).A .椭圆B .线段C .不存在D .椭圆或线段 4.与y 轴相切且和半圆224(02)x y x +=≤≤内切的动圆圆心的轨迹方程是 . 5. 设12,F F 为定点,|12F F |=6,动点M 满足12||||6MF MF +=,则动点M 的轨迹是 .1.已知三角形ABC V 的一边长为6,周长为16,求顶点A 的轨迹方程. 2.点M 与定点(0,2)F 的距离和它到定直线8y =的距离的比是1:2,求点的轨迹方程式,并说明轨迹是什么图形.§2.2.2 椭圆及其简单几何性质(1)1.根据椭圆的方程研究曲线的几何性质,并正确地画出它的图形;程研究它的性质,画图.4346,文P37~ P40找出疑惑之处)复习1:椭圆2211612x y+=上一点P到左焦点的距离是2,那么它到右焦点的距离是.复习2:方程2215x ym+=表示焦点在y轴上的椭圆,则m的取值范围是.二、新课导学※学习探究问题1:椭圆的标准方程22221x ya b+=(0)a b>>,它有哪些几何性质呢?图形:范围:x:y:对称性:椭圆关于轴、轴和都对称;顶点:(),(),(),();长轴,其长为;短轴,其长为;离心率:刻画椭圆程度.椭圆的焦距与长轴长的比ca称为离心率,记cea=,且01e<<.试试:椭圆221169y x+=的几何性质呢?图形:对称性:椭圆关于轴、轴和都对称;顶点:(),(),(),();长轴,其长为;短轴,其长为;离心率:cea== .反思:ba或cb的大小能刻画椭圆的扁平程度吗?※典型例题例1 求椭圆221625400x y+=的长轴和短轴的长、离心率、焦点和顶点的坐标.变式:若椭圆是22981x y+=呢?小结:①先化为标准方程,找出,a b,求出c;②注意焦点所在坐标轴.例 2 点(,)M x y与定点(4,0)F的距离和它到直线25:4l x=的距离的比是常数45,求点M的轨迹.小结:到定点的距离与到定直线的距离的比为常数(小于1)的点的轨迹是椭圆 .※ 动手试试练1.求适合下列条件的椭圆的标准方程:⑴焦点在x 轴上,6a =,13e =;⑵焦点在y 轴上,3c =,35e =;⑶经过点(3,0)P -,(0,2)Q -;⑷长轴长等到于20,离心率等于35.三、总结提升 ※ 学习小结1 .椭圆的几何性质:图形、范围、对称性、顶点、长轴、短轴、离心率;2 .理解椭圆的离心率.※ 知识拓展(数学与生活)已知水平地面上有一篮球,在斜平行光线的照射下,其阴影为一椭圆,且篮球与地面※ 自我评价 你完成本节导学案的情况为( ). A. 很好 B. 较好 C. 一般 D. 较差※当堂检测(时量:5分钟 满分:10分)计分:1.若椭圆2215x y m+=的离心率e =则m的值是( ).A.3 B .3或253C D 2.若椭圆经过原点,且焦点分别为1(1,0)F ,2(3,0)F ,则其离心率为( ).A .34 B.23 C .12 D .143.短轴长为,离心率23e =的椭圆两焦点为12,F F ,过1F 作直线交椭圆于,A B 两点,则2ABF ∆的周长为( ).A .3B .6C .12D .244.已知点P 是椭圆22154x y +=上的一点,且以点P 及焦点12,F F 为顶点的三角形的面积等于1,则点P 的坐标是 .5.某椭圆中心在原点,焦点在x 轴上,若长轴长为18,且两个焦点恰好将长轴三等分,则此椭圆的方程是 .1.比较下列每组椭圆的形状,哪一个更圆,哪一个更扁?⑴22936x y +=与2211612x y += ;⑵22936x y +=与221610x y += .2.求适合下列条件的椭圆的标准方程: ⑴经过点(P -,Q ;⑵长轴长是短轴长的3倍,且经过点(3,0)P ; ⑶焦距是8,离心率等于0.8.§2.2.2 椭圆及其简单几何性质(2)1.根据椭圆的方程研究曲线的几何性质;2.椭圆与直线的关系.一、课前准备(预习教材理P 46~ P 48,文P 40~ P 41找出疑惑之处)复习1: 椭圆2211612x y +=的焦点坐标是( )( ) ;长轴长 、短轴长 ;离心率 .复习2:直线与圆的位置关系有哪几种?如何判定?二、新课导学 ※ 学习探究问题1:想想生活中哪些地方会有椭圆的应用呢?问题2:椭圆与直线有几种位置关系?又是如何确定?反思:点与椭圆的位置如何判定?※ 典型例题例 1 一种电影放映灯泡的反射镜面是旋转椭圆面(椭圆绕其对称轴旋转一周形成的曲面)的一部分.过对称轴的截口BAC 是椭圆的一部分,灯丝位于椭圆的一个焦点1F 上,片门位于另一个焦点2F 上,由椭圆一个焦点1F 发出的光线,经过旋转椭圆面反射后集中到另一个焦点2F ,已知12BC F F ⊥,1 2.8F B cm =,12 4.5F F cm =,试建立适当的坐标系,求截口BAC 所在椭圆的方程.变式:若图形的开口向上,则方程是什么?小结:①先化为标准方程,找出,a b ,求出c ; ②注意焦点所在坐标轴.(理)例2 已知椭圆221259x y +=,直线l :45400x y -+=。

2. 1. 1《圆锥曲线的参数方程》导学案知识与技能:理解椭圆的参数方程,掌握参数方程的应用过程与方法:通过学习圆锥曲线的参数方程,得出参数方程与普通方程互化的方法情感、态度与价值观:通过本节课的学习,体会数学的现实应用价值,从而提高学习数学的兴趣,坚定信心教学过程:一、复习回顾1. 圆x2 + y2= r2的参数方程为2. 圆(x—a)2 + (y—b)2 = r2的参数方程为3练习.把下列参数方程化为普通方程,并说明它们各表示了什么曲线二、新课椭圆的一个参数方这是中心在原点0,焦点在x轴上的椭圆的参数方程.思考:类比圆的参数方程中参数的意义,此椭圆的参数方程中参数「的意义是什么?以原点为圆心,分别以a、b(a> b>0)为半径作两个同心圆.设A是大圆上的任一点,连接0A,与小圆交于点B.过点A, B分别作x轴,y轴的垂线,两垂线交于点M.问题:求点M的参数方程.当半径0A绕点0旋转一周时,就得到了点M的轨迹,它的参数方程是参数:是点M所对应的圆的半径0A(或0B)的旋转角(称为点M的离心角).探究:椭圆规是用来画椭圆的一种器械.它的构造如图所示.在一个十字形的金属板上有两条互相垂直的导槽,在直尺上有两个固定滑块A, B,它们可分别在纵槽和横槽中滑动,在直尺上的点M处用套管装上铅笔,使直尺转动一周就画出一个椭圆.你能说明它的构造原理吗?练习1•椭圆若共[0, 2二],则椭圆上的点(一a, 0)对应的二=(A )练习2.当参数7变化时,动点P(2cosr, 3sinT所确定的曲线必过( B )例1.在椭圆上求一点M,使点M到直线x+ 2y- 10= 0的距离最小,并求出最小距离.思考:与简单的线性规划问题进行类比,你能在实数x, y满足的前提下,求出z= x- 2y 的最大值和最小值吗?由此可以提出哪些类似的问题?例2.如图,已知椭圆上一点M(除短轴端点处)与短轴两端点B1、B2的连线分别交x轴于P、Q两点,求证|0P| • | OQ|为定值.练习3.椭圆的内接矩形的最大面积是__________ .练习4.已知A、B是椭圆与坐标轴正半轴的两交点,在第一象限的椭圆弧上求一点P, 使四边形OAPB的面积最大.课堂小结椭圆的一个参数方课后作业15 565km,短轴长为15 443 k1. 一个人造地球卫星的运行轨道是一个椭圆,长轴长为m.取椭圆中心为坐标原点,求卫星轨道的参数方程.2.已知实数x、y满足z= x+ 2y的最大值与最小值。
2.1.1椭圆及其标准方程※知识要点1.椭圆的定义:在平面内与两个定点F1、F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做________.这两定点叫做椭圆的________,两焦点间的距离叫________.集合P={M||MF1|+|MF2|=2a},|F1F2|=2c,其中a>0,c>0:(1)若______,则集合P为椭圆;(2)若______,则集合P为线段;(3)若______,则集合P为空集.焦点在x轴上焦点在y轴上标准方程图形焦点坐标a、b、c的关系(1)焦点△F1AF2周长C△F1AF2=、面积S△F1AF2=;(2)△ABF2的周长为:C△ABF2=;(3)通径:|AC|=;※课前自测1.椭圆x225+y2169=1的焦点坐标是()A.(±5,0) B.(0,±5) C.(0,±12) D.(±12,0)2.椭圆x225+y216=1上的一点P到椭圆一个焦点的距离为7,则点P到另一个焦点的距离是()A.2B.3C.5D.73.已知点M到两个定点A(-1,0)和B(1,0)的距离之和是定值2,则动点M的轨迹是()A.一个椭圆B.线段ABC.线段AB的垂直平分线D.直线AB4.椭圆x2m+y24=1的焦距是2,则m的值是()A.5B.3或8 C.3或5D.205.已知方程x225-m+y2m+9=1表示焦点在y轴上的椭圆,则m的取值范围是.※题型讲练考点一⇨椭圆的定义【例1】已知集合P={M||MF|+|MG|=10},其中F为定点且|FG|=8,若M到F的距离为2,N是MF的中点,则N点到FG中点O的距离是()A.8B.4C.2 D.32变式训练1:椭圆x225+y216=1上一点M到一个焦点的距离为4,则M到另一个点的距离为()A.4B.6 C.8D.2 考点二⇨求椭圆的标准方程【例2】求适合下列条件的椭圆的标准方程:(1)两个焦点的坐标分别为F1(-4,0)、F2(4,0),并且椭圆上一点P与两焦点的距离的和等于10;(2)焦点分别为(0,-2)、(0,2),经过点(4,32);(3)经过两点(2,-2)、(-1,142).变式训练2:(1)已知椭圆的两个焦点坐标分别是(0,-2)和(0,2),且过点(-32,52),则椭圆的标准方程为.(2)已知椭圆经过点(3,12)、(152,-14),求其标准方程.考点三⇨定义法解决轨迹问题【例3】已知B、C是两个定点,|BC|=8,且△ABC的周长等于18,求这个三角形的顶点A的轨迹方程.变式训练3:已知△ABC的周长是8,且B(-1,0)、C(1,0),则顶点A的轨迹方程是()A.x29+y28=1(x≠±3) B.x29+y28=1(x≠0)C.x24+y23=1(y≠0) D.x23+y24=1(y≠0)考点四 ⇨椭圆的焦点三角形的性质【例4】已知点P 是椭圆y 25+x 24=1上的点,F 1和F 2是焦点,且∠F 1PF 2=30°,求△F 1PF 2的面积.变式训练4:1.已知椭圆x 225+y 29=1的焦点为F 1、F 2,P 为椭圆上的一点,已知PF 1⊥PF 2,则△F 1PF 2的面积为( ) A .9 B .12 C .10 D .82.已知点P (3,4)是椭圆x 2a 2+y2b 2=1(a >b >0)上一点,F 1,F 2是椭圆的两个焦点,若PF 1→·PF 2→=0. (1)求椭圆的方程; (2)求△PF 1F 2的面积.※课堂反馈1.到两定点F 1(-2,0)和F 1(2,0)的距离之和为4的点的轨迹是( ) A .椭圆 B .线段 C .圆 D .无法确定2.设P 是椭圆x 225+y216=1上的一点,F 1,F 2是椭圆的两个焦点,则|PF 1|+|PF 2|等于( ) A .10 B .8 C .5 D .43.椭圆x 225+y216=1的焦距为( )A .4B .5C .6D .94.已知椭圆x 225+y29=1的左、右焦点分别为F 1、F 2,过点F 1的直线l 交椭圆于A ,B 两点,则△ABF 2的周长是 . 5.焦点在坐标轴上,且经过A (-2,2)和B (3,1)两点,求椭圆的标准方程.※课后练习 A 级 基础巩固一、选择题1.已知椭圆x 216+y 2b2=1过点(-2,3),则其焦距为( )A .8B .12C .23D .4 32.已知椭圆x 225+y 2m2=1(m >0)的左焦点为F 1(-4,0),则m =( ) A .2 B .3 C .4 D .93.已知F 1、F 2是椭圆x 216+y29=1的两个焦点,过点F 2的直线交椭圆于点A 、B ,若|AB |=5,则|AF 1|+|BF 1|=( ) A .11 B .10 C .9 D .164.设P 是椭圆x 216+y212=1上一点,P 到两焦点F 1、F 2的距离之差为2,则△PF 1F 2是( ) A .锐角三角形 B .直角三角形 C .钝角三角形 D .等腰直角三角形5.方程x 2m +y22m -1=1为椭圆方程的一个充分不必要条件是( )A .m >12B .m >12且m ≠1C .m >1D .m >06.已知两点F 1(-1,0)、F 2(1,0),且|F 1F 2|是|PF 1|与|PF 2|的等差中项,则动点P 的轨迹方程是( )A .x 216+y 29=1B .x 216+y 212=1C .x 24+y 23=1D .x 23+y 24=1二、填空题7.已知椭圆中心在坐标原点,焦点在x 轴上,椭圆与x 轴的一个交点到两焦点的距离分别为4和2,则椭圆的标准方程为 . 8.若以椭圆上一点和椭圆的两个焦点为顶点的三角形面积的最大值为1,则该椭圆长半轴长的最小值为 . 三、解答题9.已知椭圆的中心在原点,且经过点P (3,0),a =3b ,求椭圆的标准方程.B 级 素养提升一、选择题1.设椭圆的标准方程为x 2k -3+y 25-k=1,若其焦点在x 轴上,则k 的取值范围是( ) A .k >3 B .3<k <5 C .4<k <5 D .3<k <4 2.若曲线ax 2+by 2=1为焦点在x 轴上的椭圆,则实数a 、b 满足( )A .a 2>b 2B .1a <1b C .0<a <b D .0<b <a3.F 1、F 2是椭圆x 29+y 27=1的两个焦点,A 为椭圆上一点,且∠AF 1F 2=45°,则△AF 1F 2的面积为( )A .7B .74C .72D .7524.设椭圆x 24+y 23=1的左、右焦点分别为F 1,F 2,P 是椭圆上的一动点,若△PF 1F 2是直角三角形,则△PF 1F 2的面积为( )A .3B .3或32C .32D .6或3二、填空题5.若椭圆x 25+y 2m=1的一个焦点坐标为(0,1),则实数m 的值为 .6.设F 1,F 2为椭圆C :x 236+y 220=1的两个焦点,M 为C 上一点且在第一象限.若△MF 1F 2为等腰三角形,则M 的坐标为 .三、解答题7.根据下列条件,求椭圆的标准方程.(1)经过两点A (0,2)、B (12,3);(2)经过点(2,-3)且与椭圆9x 2+4y 2=36有共同的焦点.8.已知F 1、F 2是椭圆x 2100+y 264=1的两个焦点,P 是椭圆上任一点,若∠F 1PF 2=π3,求△F 1PF 2的面积.2.1.2椭圆的简单几何性质※知识要点焦点的位置焦点在x轴上焦点在y轴上标准方程图形对称性对称轴,对称中心范围x∈,y∈x∈,y∈顶点轴长长轴|A1A2|=,短轴|B1B2|=焦点焦距|F1F2|=离心率e=(0<e<1)(1)①动点角范围:0≤∠A1P A2≤∠A1BA2;②焦半径范围:≤|PF1|≤;③|PO|范围:≤|PO|≤;④斜率:kP A1·kP A2=.(2)离心率e越大,椭圆;e越小,椭圆.※课前自测1.点(2,3)在椭圆y2a2+x2b2=1上,则()A.点(-2,3)不在椭圆上B.点(-2,-3)不在椭圆上C.点(2,-3)在椭圆上D.无法判断点(-2,3)、(-2,-3)、(2,-3)是否在椭圆上2.椭圆5x2+ky2=5的一个焦点是(0,2),那么k的值为() A.-1B.1C.5D.- 5 3.椭圆9x2+y2=36的短轴长为()A.2 B.4 C.6 D.124.已知椭圆x2a2+y2b2=1(a>b>0)的离心率为12,则()A.a2=2b2B.3a2=4b2C.a=2b D.3a=4b5.若椭圆C:x2a2+y2b2=1(a>b>0)经过点P(0,3),且椭圆的长轴长是焦距的两倍,则a=.※题型讲练考点一⇨根据椭圆的方程研究几何性质【例1】求椭圆9x2+16y2=144的长轴长、短轴长、离心率、焦点和顶点坐标.变式训练1:设椭圆方程mx2+4y2=4m(m>0)的离心率为12,试求椭圆的长轴长和短轴长、焦点坐标及顶点坐标.考点二⇨利用椭圆的几何性质求标准方程【例2】求适合下列条件的椭圆的标准方程.(1)椭圆过点(3,0),离心率e=63;(2)在x轴上的一个焦点,与短轴两个端点的连线互相垂直,且焦距为8.变式训练2:已知椭圆E的中心在坐标原点,长轴在x轴上,离心率为32,且E上一点到E的两个焦点的距离之和为12,则椭圆E的方程为.考点三⇨求椭圆的离心率【例3】A为y轴上一点,F1、F2是椭圆的两个焦点,△AF1F2为正三角形,且AF1的中点B恰好在椭圆上,求此椭圆的离心率.变式训练3:已知点F1、F2分别是椭圆x2a2+y2b2=1的左、右焦点,过F1且垂直于x轴的直线与椭圆交于A、B两点,若△ABF2为正三角形,则该椭圆的离心率e是()A.12B.22C.13D.33考点四 ⇨直线与椭圆的位置关系【例4】已知椭圆4x 2+y 2=1及直线y =x +m .(1)当直线和椭圆有公共点时,求实数m 的取值范围; (2)求直线被椭圆截得的弦最长时直线的方程.变式训练4:已知椭圆E :x 2a 2+y 2b 2=1(a >b >0)的离心率为32,A 1,A 2分别为椭圆E 的左右顶点,B 为上顶点,△A 1BA 2的面积为2.直线l 过点D (1,0)且与椭圆E 交于P ,Q 两点. (1)求椭圆E 的标准方程; (2)求△OPQ 面积的最大值.※课堂反馈1.椭圆以两条坐标轴为对称轴,一个顶点是(0,13),另一个顶点是(-10,0),则焦点坐标为( ) A .(±13,0) B .(0,±10) C .(0,±13) D .(0,±69)2.已知直线22x -y +42=0经过椭圆x 2a 2+y 2b2=1(a >b >0)的左焦点F 1,且与椭圆在第二象限的交点为M ,与y 轴的交点为N ,F 2是椭圆的右焦点,且|MN |=|MF 2|,则椭圆的方程为( )A .x 240+y 24=1B .x 25+y 2=1C .x 210+y 2=1 D .x 29+y 25=13.椭圆x 2+y2m=1的焦点在y 轴上,长轴长是短轴长的2倍,则m 的值为( )A .12B .2C .14D .44.椭圆x 29+y 216=1的焦点坐标是 ,顶点坐标是 .5.已知椭圆的标准方程为x 24+y 29=1.(1)求椭圆的长轴长和短轴长. (2)求椭圆的离心率.(3)求以此椭圆的长轴端点为短轴端点,并且经过点P (-4,1)的椭圆方程.※课后练习 A 级 基础巩固一、选择题1.已知椭圆x 210-m +y 2m -2=1的长轴在y 轴上,若焦距为4,则m 等于( )A .4B .5C .7D .8 2.椭圆的一个顶点与两焦点组成等边三角形,则它的离心率e 为( )A .12B .13C .14D .223.与椭圆9x 2+4y 2=36有相同焦点,且短轴长为45的椭圆方程是( )A .x 225+y 220=1B .x 220+y 225=1C .x 220+y 245=1D .x 280+y 285=14.已知椭圆C :x 2a 2+y24=1的一个焦点为(2,0),则C 的离心率为( )A .13B .12C .22D .2235.已知以F 1(-2,0)、F 2(2,0)为焦点的椭圆与直线x +3y +4=0有且仅有一个交点,则椭圆的长轴长为( ) A .3 2 B .2 6 C .27 D .4 26.已知椭圆C :x 2a 2+y2b2=1(a >b >0)的左、右顶点分别为A 1,A 2,且以线段A 1A 2为直径的圆与直线bx -ay +2ab =0相切,则C 的离心率为( )A .63B .33C .23D .13二、填空题7.已知椭圆的中心在原点,若长轴长为18,且两个焦点恰好将长轴三等分,则此椭圆标准方程为 .8.已知A (2,2)是椭圆x 2m +y 24=1上一点,F 是椭圆的右焦点,设点F 到直线x =4的距离为d ,则m = ,|AF |d= .三、解答题9.已知椭圆x 249+y 224=1上一点P 与椭圆的两个焦点F 1、F 2的连线互相垂直.(1)求椭圆的离心率; (2)求△PF 1F 2的面积.B 级 素养提升一、选择题1.已知椭圆的对称轴是坐标轴,离心率为13,长轴长为12,则椭圆方程为( )A .x 2144+y 2128=1或x 2128+y 2144=1 B.x 26+y 24=1C .x 236+y 232=1或x 232+y 236=1 D.x 24+y 26=1或x 26+y 24=12.已知椭圆C :x 2a 2+y2b2=1(a >b >0)的左、右焦点为F 1、F 2,离心率为33,过F 2的直线l 交C 于A 、B 两点,若△AF 1B 的周长为43,则C 的方程为( )A .x 23+y 22=1B .x 23+y 2=1C .x 212+y 28=1D .x 212+y 24=13.已知直线l 过点(3,-1),且椭圆C :x 225+y236=1,则直线l与椭圆C 的公共点的个数为( ) A .1 B .1或2 C .2 D .04.从椭圆x 2a 2+y2b2=1(a >b >0)上一点P 向x 轴作垂线,垂足恰为左焦点F 1,A 是椭圆与x 轴正半轴的交点,B 是椭圆与y 轴正半轴的交点,且AB ∥OP (O 是坐标原点),则该椭圆的离心率是( )A .24B .12C .22D .32二、填空题5.已知点P (0,1),椭圆x 24+y 2=m (m >1)上两点A ,B 满足AP →=2PB →,则当m = 时,点B 横坐标的绝对值最大.6.设A ,B 是椭圆C :x 23+y 2m=1长轴的两个端点.若C 上存在点M 满足∠AMB =120°,则m 的取值范围是 . 三、解答题7.已知椭圆M :x 2a 2+y 2b 2=1(a >b >0)的离心率为63,焦距为2 2.斜率为k 的直线l 与椭圆M 有两个不同的交点A ,B . (1)求椭圆M 的方程;(2)若k =1,求|AB |的最大值;8.设椭圆x 2a 2+y 2b2=1(a >b >0)的左焦点为F ,上顶点为B .已知椭圆的短轴长为4,离心率为55.(1)求椭圆的方程;(2)设点P 在椭圆上,且异于椭圆的上、下顶点,点M 为直线PB 与x 轴的交点,点N 在y 轴的负半轴上,若|ON |=|OF |(O 为原点),且OP ⊥MN ,求直线PB 的斜率.2.2.1 双曲线及其标准方程※知识要点1.双曲线的定义平面内,动点P 与两个定点F 1、F 2(|F 1F 2|=2c >0)的距离之差的绝对值 为常数2a (2a <2c ),则点P 的轨迹叫________.这两个定点叫双曲线的________,两焦点间的距离叫________. 注意:集合P ={M |||MF 1|-|MF 2||=2a },|F 1F 2|=2c ; (1)当________时,P 点的轨迹是________; (2)当________时,P 点的轨迹是________; (3)当________时,P 点不存在. 焦点在x 轴上焦点在y 轴上标准方程图形焦点坐标a ,b ,c 关系※课前自测1.平面内,到两定点F 1(-3,0)、F 2(3,0)的距离之差的绝对值等于6的点M 的轨迹是( ) A .椭圆 B .线段 C .双曲线 D .两条射线 2.焦点在坐标轴上,中心在原点,且经过点P (27,3)和点Q (-7,-62)的双曲线方程是( )A .x 225-y 275=1 B.x 225-y 275=1或y 225-x 275=1C .x 225-y 275=1或y 275-x 225=1 D.y 275-x 225=13.双曲线方程为x 2-2y 2=1,则它的右焦点坐标为( ) A .(22,0) B .(52,0) C .(62,0) D .(3,0)4.双曲线的焦点在x 轴上,且经过点M (3,2)、N (-2,-1),则双曲线标准方程是 .5.已知双曲线过点(5,0),且与椭圆x 230+y 25=1有相同的焦点,求双曲线的方程.※题型讲练考点一 ⇨双曲线定义的应用【例1】椭圆x 2m +y 2n =1(m >n >0)与双曲线x 2a -y 2b=1(a >0,b >0)有相同的焦点F 1,F 2,且P 是这两条曲线的一个交点,则|PF 1|·|PF 2|等于__m -a __.变式训练1:P 是双曲线x 264-y 236=1上一点,F 1、F 2是双曲线的两个焦点,且|PF 1|=17,则|PF 2|的值为 .考点二 ⇨待定系数法求双曲线的标准方程【例2】(1)已知双曲线的焦点在y 轴上,并且双曲线经过点(3,-42)和(94,5),求双曲线的标准方程;(2)求与双曲线x 216-y 24=1有公共焦点,且过点(32,2)的双曲线方程.变式训练2:求适合下列条件的双曲线的标准方程:(1)双曲线的一个焦点坐标是(0,-6),经过点A (-5,6);(2)与椭圆x 216+y 225=1共焦点,且过点(-2,10).考点三 ⇨双曲线的焦点三角形问题【例3】设双曲线x 24-y 29=1,F 1、F 2是其两个焦点,点P 在双曲线右支上.(1)若∠F 1PF 2=90°,求△F 1PF 2的面积; (2)若∠F 1PF 2=60°时,△F 1PF 2的面积是多少?若∠F 1PF 2=120°时,△F 1PF 2的面积又是多少?变式训练3:若F 1、F 2是双曲线x 29-y 216=1的两个焦点,P 在双曲线上,且|PF 1|·|PF 2|=32,求∠F 1PF 2的大小.考点四 ⇨分类讨论思想的应用【例4】已知方程kx 2+y 2=4,其中k 为实数,对于不同范围的k 值分别指出方程所表示的曲线类型.变式训练4:1.讨论方程x 25-m +y 22-m=1(m <3)所表示的曲线类型.2.已知双曲线8kx 2-ky 2=8的一个焦点为(0,3),求k 的值.※课堂反馈 1.椭圆x 24+y 2a 2=1与双曲线x 2a -y 22=1有相同的焦点,则a 的值是( )A .12B .1C .1或-2D .1或122.已知m ,n ∈R ,则方程x 2m +y 2n =1中“m ·n <0”是“方程x 2m+y2n=1表示双曲线”的( ) A .充分不必要条件 B .必要不充分条件 C .充分必要条件 D .既不充分也不必要条件 3.设动点P 到A (-5,0)的距离与它到B (5,0)距离的差等于6,则P 点的轨迹方程是( )A .x 29-y 216=1B .y 29-x 216=1C .x 29-y 216=1(x ≤-3)D .x 29-y 216=1(x ≥3)4.双曲线C :x22-y 2=1的左右焦点分别为F 1,F 2,P 是双曲线右支上一点,则|PF 1|-|PF 2|= ,离心率e = . 5.根据下列条件,求双曲线的标准方程: (1)c =6,经过点(-5,2),且焦点在x 轴上.(2)已知双曲线两个焦点的坐标为F 1(0,-5),F 2(0,5),双曲线上一点P 到F 1,F 2的距离之差的绝对值等于6.※课后练习 A 级 基础巩固一、选择题1.已知M (-2,0)、N (2,0),|PM |-|PN |=4,则动点P 的轨迹是( ) A .双曲线 B .双曲线左支 C .一条射线 D .双曲线右支2.双曲线3x 2-4y 2=-12的焦点坐标为( )A .(±5,0)B .(0,±5)C .(±7,0)D .(0,±7)3.已知x 21+k -y 21-k=1表示双曲线,则k 取值范围是( )A .-1<k <1B .k >0C .k ≥0D .k >1或k <-1 4.已知双曲线2mx 2-my 2=4的一个焦点为(0,6),则m 的值为( )A .1B .-1C .73D .-735.双曲线x23-y 2=1的焦点坐标是( )A .(-2,0),(2,0)B .(-2,0),(2,0)C .(0,-2),(0,2)D .(0,-2),(0,2)6.若双曲线E :x 29-y 216=1的左、右焦点分别为F 1、F 2,点P在双曲线E 上,且|PF 1|=3,则|PF 2|等于( ) A .11 B .9 C .5 D .3 二、填空题7.已知椭圆x 2a 2+y 29=1(a >0)与双曲线x 24-y 23=1有相同的焦点,则a 的值为 .8.已知双曲线x 225-y 29=1的两个焦点分别为F 1、F 2,若双曲线上的点P 到点F 1的距离为12,则点P 到点F 2的距离为 . 三、解答题9.求满足下列条件的双曲线的标准方程. (1)焦点在x 轴上,c =6且经过点(-5,2);(2)过P (3,154)和Q (-163,5)两点.B 级 素养提升一、选择题1.已知双曲线中心在原点,一个焦点为F 1(-5,0),点P 在该双曲线上,线段PF 1的中点坐标为(0,2),则双曲线的方程是( )A .x 24-y 2=1B .x 2-y 24=1C .x 22-y 23=1D .x 23-y 22=12.已知F 是双曲线C :x 2-y23=1的右焦点,P 是C 上一点,且PF ⊥x 轴,点A 的坐标是(1,3),则△APF 的面积为( )A .13B .12C .23D .323.双曲线x 2a 2-y2b2=1右焦点为F ,点A 在双曲线的右支上,以AF 为直径的圆M 与圆x 2+y 2=a 2的位置关系是( ) A .相交 B .外切 C .相离 D .内切4.已知双曲线的左、右焦点分别为F 1、F 2,过F 1的直线与双曲线的左支交于A 、B 两点,线段AB 的长为5,若2a =8,那么△ABF 2的周长是( ) A .16 B .18 C .21 D .26 二、填空题5.设双曲线与椭圆x 227+y 236=1有共同的焦点,且与椭圆相交,有一个交点的坐标为(15,4),则此双曲线的方程为 . 6.已知F 1、F 2为双曲线C :x 2-y 2=1的左、右焦点,点P 在C 上,∠F 1PF 2=60°,则|PF 1|·|PF 2|等于 .三、解答题7.已知双曲线方程为2x 2-y 2=k ,焦距为6,求k 的值.8.当0°≤α≤180°时,方程x 2cos α+y 2sin α=1表示的曲线如何变化?2.2.2 双曲线的简单几何性质※知识要点1.双曲线的简单几何性质 焦点位置 焦点在x 轴上焦点在y 轴上双曲线 方程图形范围对称性 对称轴: 对称中心: 顶点 渐近线离心率e =ca,e ∈ ,其中c =a 2+b 2 e 越大,张口越大,e 越小,张口越小(1)动点P 到同侧焦点F 2的距离|PF 2|最小=|A 2F 2|= ; (2)焦点到渐近线的距离为:|F 2M |= ; (2)渐近线求法结论:可直接令方程x 2a 2-y 2b2=λ(λ≠0)等号右边的常数为0,化简解得;※课前自测1.双曲线x 225-y29=1的顶点坐标是( )A .(±5,0)B .(±5,0)或(0,±3)C .(±4,0)D .(±4,0)或(0,±3) 2.渐近线方程为x ±y =0的双曲线的离心率是( ) A .22B .1C . 2D .23.双曲线方程为x 24-y 2=1,则渐近线方程为( )A .y =±12xB .y =±2xC .y =±xD .y =12x4.已知双曲线x 2a 2-y25=1(a >0)的右焦点为(3,0),则该双曲线的离心率等于( )A .34B .32C .3D .45.双曲线x 22-y 2=1的焦距是23 ,渐近线方程是 .6.已知中心在原点的双曲线的渐近线方程是y =±3x ,且双曲线过点(2,3). (1)求双曲线的方程;(2)求双曲线的焦点到渐近线的距离.※题型讲练考点一 ⇨根据双曲线方程研究其几何性质【例1】求双曲线9y 2-4x 2=-36的顶点坐标、焦点坐标、实轴长、虚轴长、离心率和渐近线方程,并作出草图.变式训练1:求双曲线4x 2-y 2=4的顶点坐标、焦点坐标、实半轴长、虚半轴长、离心率和渐近线方程,并作出草图.考点二 ⇨利用几何性质求双曲线的标准方程 【例2】求适合下列条件的双曲线的标准方程:(1)实轴长为8,离心率为54;(2)已知双曲线的中心在原点,焦点F 1、F 2在坐标轴上,实轴长和虚轴长相等,且过点P (4,-10).变式训练2:(1)顶点间距离为6,渐近线方程为y =±32x ,则双曲线的方程为 .(2)与双曲线x 2-2y 2=2有公共渐近线,且过点M (2,-2)的双曲线方程为 .考点三⇨双曲线的离心率【例3】设双曲线x2a2-y2b2=1(a>0,b>0)的左、右焦点分别为F1,F2,P是双曲线上一点,点P到坐标原点O的距离等于双曲线焦距的一半,且|PF1|+|PF2|=4a,则双曲线的离心率是.变式训练3:(1)若双曲线x2a2-y2b2=1两条渐近线互相垂直,则离心率为()A.2B.32C.3D.2(2)若双曲线x2a2-y2b2=1的一条渐近线经过点(3,-4),则此双曲线的离心率为()A.73B.54C.43D.53考点四⇨直线与双曲线的位置关系【例4】已知曲线C:x2-y2=1和直线l:y=kx-1.(1)若l与C有两个不同的交点,求实数k的取值范围;(2)若l与C交于A、B两点,O是坐标原点,且△AOB的面积为2,求实数k的值.变式训练5:已知双曲线方程为2x2-y2=2.(1)过定点P(2,1)作直线交双曲线于P1,P2两点,当点P(2,1)是弦P1P2的中点时,求此直线方程.(2)过定点Q(1,1)能否作直线l,使直线l与此双曲线相交于Q1,Q2两点,且Q是弦Q1Q2的中点?若存在,求出直线l的方程;若不存在,说明理由.※课堂反馈1.设双曲线x2a2-y29=1(a>0)的渐近线方程为3x±2y=0,则a的值为()A.4B.3C.2D.12.“m=1”是“双曲线x2m-y23=1的离心率为2”的() A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件3.双曲线x2a2-y2b2=1(a>0,b>0)的离心率为3,则其渐近线方程为()A.y=±2x B.y=±3x C.y=±22x D.y=±32x 4.若双曲线x2a2-y24=1(a>0)的离心率为52,则a=. 5.求双曲线y2-2x2=1的离心率和渐近线方程.※课后练习A级基础巩固一、选择题1.以椭圆x216+y29=1的顶点为顶点,离心率为2的双曲线方程为()A.x216-y248=1 B.y29-x227=1C.x216-y248=1或y29-x227=1 D.以上都不对2.双曲线2x2-y2=8的实轴长是()A.2B.22C.4D.4 23.若a>1,则双曲线x2a2-y2=1的离心率的取值范围是() A.(2,+∞) B.(2,2) C.(1,2) D.(1,2) 4.已知双曲线C:x2a2-y2b2=1(a>0,b>0)的离心率为2,则点(4,0)到C的渐近线的距离为()A. 2 B.2 C.322D.2 25.双曲线C :x 24-y 22=1的右焦点为F ,点P 在C 的一条渐近线上,O 为坐标原点,若|PO |=|PF |,则△PFO 的面积为( )A .324B .322C .2 2D .3 26.以双曲线y 2-x 23=1的一个焦点为圆心,离心率为半径的圆的方程是( )A .(x -2)2+y 2=4B .x 2+(y -2)2=2C .(x -2)2+y 2=2D .x 2+(y -2)2=4 二、填空题7.在平面直角坐标系xOy 中,若双曲线x 2-y 2b2=1(b >0)经过点(3,4),则该双曲线的渐近线方程是 .8.已知双曲线x 2a 2-y 2b2=1(a >0,b >0)的一条渐近线为2x +y =0,一个焦点为(5,0),则a = ;b = . 三、解答题9.(1)求与椭圆x 29+y 24=1有公共焦点,且离心率e =52的双曲线的方程;(2)求虚轴长为12,离心率为54的双曲线的标准方程.B 级 素养提升一、选择题1.已知方程ax 2-ay 2=b ,且a 、b 异号,则方程表示( ) A .焦点在x 轴上的椭圆 B .焦点在y 轴上的椭圆 C .焦点在x 轴上的双曲线 D .焦点在y 轴上的双曲线2.双曲线x 2-y2m=1的离心率大于2的充分必要条件是( )A .m >12B .m ≥1C .m >1D .m >23.已知M (x 0,y 0)是双曲线C :x 22-y 2=1上的一点,F 1、F 2是C 的两个焦点.若MF 1→·MF 2→<0,则y 0的取值范围是( )A .(-33,33)B .(-36,36)C .(-223,223)D .(-233,233)4.已知双曲线C :x 2a 2-y 2b2=1(a >0,b >0),过左焦点F 的直线切圆x 2+y 2=a 2于点P ,交双曲线C 右支于点Q ,若FP →=PQ →,则双曲线C 的渐近线方程为( )A .y =±xB .y =±2xC .y =±12xD .y =±32x二、填空题5.已知双曲线x 29-y 2m=1的一个焦点在圆x 2+y 2-4x -5=0上,则双曲线的渐近线方程为 .6.在平面直角坐标系xOy 中,若双曲线x 2a 2-y 2b 2=1(a >0,b >0)的右焦点F (c ,0) 到一条渐近线的距离为32c ,则其离心率的值为 . 三、解答题7.焦点在x 轴上的双曲线过点P (42,-3),且点Q (0,5)与两焦点的连线互相垂直,求此双曲线的标准方程.8.双曲线x 2a 2-y 2b2=1(a >0,b >0)的右焦点为F (c ,0).(1)若双曲线的一条渐近线方程为y =x 且c =2,求双曲线的方程;(2)以原点O 为圆心,c 为半径作圆,该圆与双曲线在第一象限的交点为A ,过A 作圆的切线,其斜率为-3,求双曲线的离心率.2.3.1抛物线及其标准方程※知识要点1.抛物线的定义(1)定义:平面内与一个定点F和一条定直线l(l不经过点F)距离的点的轨迹.(2)焦点:叫做抛物线的焦点.(3)准线:叫做抛物线的准线..抛物线的标准方程标准方程p的几何意义:焦点F到准线l的距离图形焦点准线方程开口方向※课前自测1.抛物线y2=4x的焦点坐标是()A.(0,2)B.(0,1)C.(2,0)D.(1,0)2.抛物线y=14x2的准线方程为()A.x=-116B.x=-18C.y=-1 D.y=23.y=2x2的焦点坐标是()A.(1,0) B.(14,0) C.(0,14) D.(0,18)4.抛物线x2=-2py(p>0)的焦点是双曲线y23-x26=1的一个焦点,则该抛物线的方程是.5.求满足下列条件的抛物线的标准方程.(1)准线方程为2y+4=0;(2)过点(3,-4);(3)焦点在直线x+3y+15=0上.※题型讲练考点一⇨求抛物线的焦点及准线【例1】设抛物线的方程为y=ax2(a≠0),求抛物线的焦点坐标与准线方程.变式训练1:(1)抛物线C:y=-x28的焦点坐标为;(2)抛物线x2=-y的准线方程为.考点二⇨抛物线的标准方程【例2】求满足下列条件的抛物线的标准方程.(1)焦点在直线3x+4y-12=0上;(2)焦点是(-2,0);(3)准线是y=-32;(4)焦点到准线的距离是2.变式训练2:求满足下列条件的抛物线的标准方程:(1)过点(-3,2);(2)焦点在直线x-2y-4=0上.考点三⇨抛物线定义的应用【例3】(1)设抛物线y2=8x上一点P到y轴的距离是4,则点P到该抛物线焦点的距离是()A.4B.6C.8D.12(2)过点A(1,0),且与直线l:x=-1相切的圆的圆心的轨迹是()A.圆B.椭圆C.双曲线D.抛物线变式训练3:(1)已知抛物线y2=4x上一点M与该抛物线的焦点F的距离|MF|=4,则点M的横坐标x=;(2)已知抛物线y2=4x上一点P到焦点F的距离为5,则△PFO 的面积为.考点四⇨抛物线在实际问题中的应用【例4】如图是抛物线形拱桥,当水面在l时,拱顶离水面2 m,水面宽4 m.水位下降1 m后,求水面的宽度.变式训练4:如图(1)所示,花坛水池中央有一喷泉,水管O′P=1 m,水从喷头P喷出后呈抛物线状,先向上至最高点后落下,若最高点距水面2 m,P距抛物线的对称轴1 m,则水池的直径至少应设计多少米?(精确到1 m)图(1)※课堂反馈1.抛物线x=4y2的焦点坐标是()A.(0,1) B.(0,-1) C.(-116,0) D.(116,0) 2.抛物线y2=2px(p>0)上一点M到焦点的距离是a(a>p2),则点M的横坐标是()A.a+p2B.a-p2C.a+p D.a-p3.若椭圆x23+4y2p2=1(p>0)的左焦点在抛物线y2=2px的准线上,则p为.4.若抛物线y2=2px(p≠0)的焦点与双曲线x22-y22=1的右焦点重合,则实数p=.5.抛物线y2=-2px(p>0)上有一点M的横坐标为-9,它到焦点的距离为10,求此抛物线方程和M点的坐标.※课后练习A级基础巩固一、选择题1.若A是定直线l外一定点,则过点A且与直线l相切的圆的圆心轨迹为()A.直线B.椭圆C.线段D.抛物线2.如果抛物线y2=2px的准线是直线x=-2,那么它的焦点坐标为()A.(1,0) B.(2,0) C.(3,0) D.(-1,0) 3.抛物线x2=4y的焦点到准线的距离为()A.12B.1 C.2 D.44.抛物线y=2x2的焦点坐标是() A.(1,0) B.()14,0C.()0,18D.()0,14 5.抛物线y2=4x上一点M到焦点的距离为1,则点M的纵坐标是()A.0 B.1516C.78D.17166.O为坐标原点,F为抛物线C:y2=42x的焦点,P为C上一点,若|PF|=42,则△POF的面积为()A.2 B.2 2 C.2 3 D.4二、填空题7.若抛物线y 2=2px 的焦点坐标为(1,0),则p = ,准线方程为 .8.沿直线y =-2发出的光线经抛物线y 2=ax 反射后,与x 轴相交于点A (2,0),则抛物线的准线方程为 (提示:抛物线的光学性质:从焦点发出的光线经抛物线反射后与轴平行). 三、解答题9.过抛物线y 2=2px (p >0)的焦点F 任作一条直线,交抛物线于P 1、P 2两点,求证:以P 1P 2为直径的圆和该抛物线的准线相切.B 级 素养提升一、选择题1.已知双曲线x 2a 2-y 2b2=1(a >0,b >0)的一条渐近线的斜率为2,且右焦点与抛物线y 2=43x 的焦点重合,则该双曲线的离心率等于( ) A . 2 B . 3 C .2 D .2 3 2.抛物线y 2=8x 的焦点到直线x -3y =0的距离是( ) A .2 3B .2C . 3D .13.若抛物线y 2=2px 的焦点与椭圆x 26+y22=1的右焦点重合,则p 的值为( ) A .-2 B .2 C .-4 D .44.已知双曲线E :x 2a 2-y2b2=1(a >0,b >0)的右顶点为A ,抛物线C :y 2=8ax 的焦点为F .若在E 的渐近线上存在点P ,使得AP →⊥FP →,则E 的离心率的取值范围是( )A .(1,2)B .(1,324]C .[324,+∞) D .(2,+∞) 二、填空题5.点M (5,3)到抛物线x 2=ay (a >0)的准线的距离为6,则抛物线的方程是 .6.若动点M (x ,y )到点F (4,0)的距离比它到直线x +5=0的距离小1,则点M 的轨迹方程是 . 三、解答题7.已知抛物线的焦点在x 轴上,抛物线上的点M (-3,m )到焦点的距离是5.求抛物线方程和m 的值.8.如图,一隧道内设双行线公路,其截面由一个长方形和抛物线构成,为保安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要0.5 m .若行驶车道总宽度AB 为6 m ,计算车辆通过隧道的限制高度是多少米?(精确到0.1 m)2.3.2抛物线的简单几何性质※知识要点1.抛物线的简单几何性质标准方程图象p的几何意义:焦点F到准线l的距离范围对称顶点焦点准线2.焦半径与焦点弦结论抛物线y2=2px(p>0)焦点弦AB,设A(x1,y1)、B(x2,y2),AB的中点E,准线为l. (其中,α为直线AB的倾斜角)(1)焦半径:|AF|=|AD|=,|BF|=|BC|=;(2)焦点弦:|AB|==2psin2α;(3) x1·x2=,y1·y2=;(4) S△OAB=p22sinα;(5)以AB为直径的圆必与准线相切于点H.※课前自测1.顶点在原点,对称轴是y轴,且通径为2的抛物线的标准方程为()A.x2=±2y B.x2=±y C.y2=±x D.y2=±2x 2.顶点在原点、坐标轴为对称轴的抛物线,过点(-1,2),则它的方程是()A.y=2x2或y2=-4x B.y2=-4x或x2=2yC.x2=-12y D.y2=-4x3.设抛物线y2=8x上一点P到y轴的距离为4,则点P到该抛物线焦点的距离为()A.6B.7C.8D.124.过抛物线y2=8x的焦点,作倾斜角为45°的直线,则被抛物线截得的弦长为()A.8B.16 C.32 D.615.已知抛物线的焦点F在x轴上,直线l过F且垂直于x轴,l与抛物线交于A、B两点,O为坐标原点,若△OAB的面积等于4,求此抛物线的标准方程.※题型讲练考点一⇨待定系数法求抛物线的标准方程【例1】已知抛物线关于y轴对称,它的顶点在坐标原点,并且经过点M(3,-23),求它的方程.变式训练1:已知抛物线的顶点在原点,对称轴为坐标轴,准线过椭圆x216+y252=1的焦点,求抛物线的方程.考点二⇨抛物线的焦点弦与焦半径问题【例2】求过抛物线y2=2px(p>0)的焦点F的弦长的最小值.变式训练2:过抛物线y2=2px(p>0)的焦点F作倾斜角为45°的直线交抛物线于A,B两点,若线段AB的长为8,求p的值.考点三 ⇨最值问题【例3】设P 是抛物线y 2=4x 上的一个动点,F 为抛物线焦点. (1)求点P 到点A (-1,1)的距离与点P 到直线x =-1的距离之和的最小值;(2)若B (3,2),求|PB |+|PF |的最小值.变式训练3:(1)定点M ()3,103与抛物线y 2=2x 上的点P 之间的距离为d 1,P 到抛物线准线l 的距离为d 2,则d 1+d 2取最小值时,P 点坐标为( )A .(0,0)B .(1,2)C .(2,2)D .()18,-12 (2)设P 是抛物线y 2=2x 上任一点,则P 到直线x -y +3=0的距离的最小值为 ,点P 的坐标为 .考点四 ⇨与抛物线有关的定点、定值、最值问题【例4】如图,过抛物线y 2=x 上一点A (4,2)作倾斜角互补的两条直线AB 、AC 交抛物线于B 、C 两点,求证:直线BC 的斜率是定值.变式训练4:过抛物线y 2=2px (p >0)的顶点任意作两条互相垂直的弦OA 、OB .求证:直线AB 过抛物线对称轴上的一定点.※课堂反馈1.顶点在原点,对称轴是y 轴,并且顶点与焦点的距离等于3的抛物线的标准方程是( ) A .x 2=±3y B .y 2=±6x C .x 2=±12y D .x 2=±6y2.抛物线y =4x 2的焦点到准线的距离是( )A .4B .2C .18D .1163.抛物线y 2=x 上一点P 到焦点的距离是2,则点P 的坐标为( )A .⎝⎛⎭⎫32,±62B .⎝⎛⎭⎫74,±72C .⎝⎛⎭⎫94,±32D .⎝⎛⎭⎫52,±102 4.设抛物线y 2=2px (p >0)的焦点为F ,点A (0,2).若线段F A 的中点B 在抛物线上,则点B 到该抛物线准线的距离为 .5.已知双曲线C 1:x 2a 2-y 2b2=1(a >0,b >0)的离心率为2,若抛物线C 2:x 2=2py (p >0)的焦点到双曲线C 1的渐近线的距离为2,求抛物线C 2的方程.※课后练习 A 级 基础巩固一、选择题 1.过抛物线y 2=2px (p >0)的焦点且垂直于x 轴的弦为AB ,O 为抛物线顶点,则∠AOB 的大小( ) A .小于90° B .等于90° C .大于90° D .不能确定 2.若AB 为抛物线y 2=4x 的弦,且A (x 1,4)、B (x 2,2),则|AB |=( ) A .13 B .13 C .6 D .4 3.若抛物线y 2=x 上一点P 到准线的距离等于它到顶点的距离,则点P 的坐标为( )A .(14,±24)B .(18,±24)C .(14,24)D .(18,24)4.若抛物线y 2=2px (p >0)的焦点是椭圆x 23p +y2p=1的一个焦点,则p =( ) A .2 B .3 C .4 D .8。