01-哈工大机械原理大作业任务书-连杆机构参考模板
- 格式:docx
- 大小:807.01 KB
- 文档页数:8
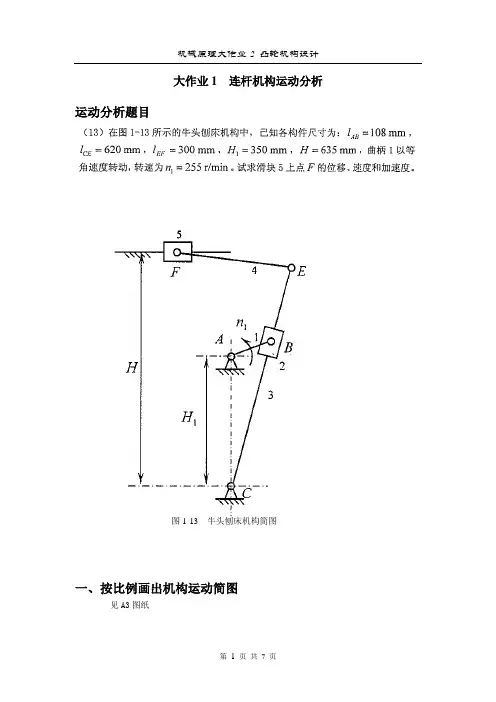
大作业1 连杆机构运动分析运动分析题目图1-13 牛头刨床机构简图一、按比例画出机构运动简图见A3图纸二、机构的结构分析及基本杆组的划分(1)机构的结构分析该机构为平面连杆机构,活动构件数n=5;有A、B、C、E、F五个转动副和B、F两个移动副,没有高副,故低副数PL=7,高副数PH=0。
机构的自由度F=3n-2PL-PH=3*5-2*7=1。
机构有确定运动轨迹。
(2)基本杆组的划分图1-13中,原动件构件1为Ⅰ级杆组,移除之后按照拆杆组法对机构进行拆分,可得由滑块2和杆3组成的RPRⅡ级杆组,以及由杆4和滑块5组成的RRPⅡ级杆组。
拆分图如下:图1-13-1 Ⅰ级杆组图1-13-2 RPRⅡ级杆组图1-13-3 RRPⅡ级杆组三、各杆组的运动分析数学模型图1-13-1 Ⅰ级杆组 x B =x A +l AB cos ϕy B =y A +l AB sin ϕ图1-13-2 RPR Ⅱ级杆组 x E =x B +(l CE -s)cos ϕj y E =y B +(l CE -s)sin ϕjϕj =arctan(B 0/A 0)A 0=xB -x CB 0=y B -y CS =2020B A + 图1-13-3 RRP Ⅱ级杆组F 的位置 x F =x E -l EF cos ϕiy F =y E +l EF sin ϕi ϕi =arcsin(A 1/l EF )A 1=H-H 1-y EF 的速度F 的加速度四、建立坐标系以A 为原点建立坐标系,则A (0,0)五、编程使用MATLAB 编写程序如下lAB=108;lCD=620;lEF=300;H1=350;H=635;xC=0;yC=-350;syms t;f=(255*pi/30)*t;xB=lAB*cos(f);yB=lAB*sin(f);A0=xB-xC;B0=yB-yC;S=sqrt(A0^2+B0^2);f1=atan(B0/A0);xE=xB+(lAB-S)*cos(f1);yE=yB+(lAB-S)*sin(f1);A1=H-H1-yE;f2=asin(A1/lEF);xF=xE-lEF*cos(f2);yF=yE+lEF*sin(f2);a=0:0.001:0.5;xF=subs(xF,t,a);plot(a,xF)title('位移x随时间t变化图像') xlabel('t(s)'),ylabel(X')lAB=108;lCD=620;lEF=300;H1=350;H=635;xC=0;yC=-350;syms t;f=(255*pi/30)*t;xB=lAB*cos(f);yB=lAB*sin(f);A0=xB-xC;B0=yB-yC;S=sqrt(A0^2+B0^2);f1=atan(B0/A0);xE=xB+(lAB-S)*cos(f1);yE=yB+(lAB-S)*sin(f1);A1=H-H1-yE;f2=asin(A1/lEF);xF=xE-lEF*cos(f2);yF=yE+lEF*sin(f2);vF=diff(xF,t);a=0:0.001:0.5;vF=subs(vF,t,a);plot(a,vF)title('速度v随时间t变化图像') xlabel('t(s)'),ylabel(V')lAB=108;lCD=620;lEF=300;H1=350;H=635;xC=0;yC=-350;syms t;f=(255*pi/30)*t;xB=lAB*cos(f);yB=lAB*sin(f);A0=xB-xC;B0=yB-yC;S=sqrt(A0^2+B0^2);f1=atan(B0/A0);xE=xB+(lAB-S)*cos(f1);yE=yB+(lAB-S)*sin(f1);A1=H-H1-yE;f2=asin(A1/lEF);xF=xE-lEF*cos(f2);yF=yE+lEF*sin(f2);aF=diff(xF,t,2);a=0:0.001:0.5;aF=subs(aF,t,a);plot(a,aF)title('加速度a随时间t变化图像') xlabel('t(s)'),ylabel(A')六、位移、速度、加速度图像位移xE随时间t变化图像速度vE随时间t变化图像加速度aE随时间t变化图像七、运动分析由MATLAB编程后绘制所得图线分析可知,牛头刨床的刨头F行程约为500mm,在0.06s~0.17s之间速度和加速度波动较大,在0.17s~0.29s 之间速度和加速度波动较小,这就保证了刨头在空行程时有急回运动,而在工作行程是由较均匀的切削速度,运动连续,且运动性能良好稳定。

Harbin Institute of Technology机械原理大作业设计说明书(一)课程名称:机械原理设计题目:连杆运动分析(16)院系:能源科学与工程学院班级:1102201设计者:学号:指导教师:赵永强唐德威设计时间:2013年6月8 日哈尔滨工业大学1 连杆机构运动分析题目16:如图所示机构,已知机构各构件的尺寸为AC l =CE l =100mm ,BC l =CD l =200mm ,90BCD ∠=,构件1的角速度为10/rad s ,试求构件5的角位移、角速度和角加速度,并对计算结果进行分析。
2 分析过程2.1 建立坐标系建立以点E 为原点的固定平面直角坐标系x-E-y,如图所示:图2 机构坐标系2.2结构分析将构件BCD 分为杆3和杆4。
该机构由2个Ⅰ级杆组RR (杆1和杆5)和两个Ⅱ级杆组RRP (杆3、杆4和滑块B 、D )。
其中原动件为杆1。
现将杆组分为如下两部分:图1 机构运动简图RRPRR图3 各级杆组2.3 建立数学模型2.3.1构件1、2、3的分析原动件杆1的转角:1θ=0—360。
原动件杆1的角速度:1ω=.1θ=10/rad s原动件杆1的角加速度:..1αθ==0运动副A 的坐标:0200A A x y mm =⎫⎬=⎭运动副A 的速度及加速度都为零。
构件1为BC (RRP Ⅱ级杆组)上滑块B 的导路 滑块B 的位置为:132cos cos B A C x x s x l θθ=+=+ 132sin sin B A C y y s x l θθ=+=+消去s,得:212arcsinA l θθ=+式中:011()sin ()cos C A C A A x x y y θθ=---构件3的角速度i ω和滑块B 沿导路的移动速度D υ:.211213(Q sin Q cos )/Q ωϕθθ==-+ 1322323(Q cos Q sin )/Q D s l l υθθ⋅==-+式中:..11111211321212Q sin ;Q cos ;Q sin sin cos sin l l l θθθθθθθθ=-==+构件3的角加速度和滑块B 沿导路移动的加速度:..241513(Q sin Q cos )/Q αθθθ==-+..4325323(Q cos Q sin )/Q B s l l υθθ==-+式中:122......21142211111Q cos sin cos 2sin l l l s θθθθθθθθ=---- 122......21152211111Q sin cos sin 2cos l l l s θθθθθθθθ=+-+2.3.2 构件3,4,5的分析构件3,4,5,由1个Ⅰ级基本杆组和一个RRP Ⅱ级杆组组成,与构件1,2,3结构相同,只运动分析过程与其相反。


Harbin Institute of Technology机械原理大作业——连杆机构运动分析课程名称:机械原理院系:能源科学与工程学院班级:完成者:学号:题号: 16任课教师:丁刚完成内容:在完成题目计算要求的同时,扩展了内容,程序为该结构的通用程序,可解决机构在不同条件下的运动情况,文本最末为几种情况的分析哈尔滨工业大学16、如图所示机构,已知机构各构件的尺寸为,试求构件5的角位移、角速度和角加速度,并对计算结构进行分析。
(1)、结构分析从侧面看原机构为此机构分为级杆组(原动件1),级杆组RRP(2号套筒、3号杆),级杆组RRP(4号套筒、5号杆)(2)、建立坐标系(3)、各个杆组的运动分析采用逆推法,从RRP杆组(4号套筒、5号杆)开始分析已知,,,,现在假定已知,,其中,,,即消去,可得可求得,也可以通过书上3-23式求得通过正弦定理可求得再来看看角速度关系对于加速度,有如下关系其中到此4、5杆就分析完毕了,别忘记之前的假设,我假设了已知,,为求,,,现在来分析RRP杆组(2号套筒、3号杆)已知,,,已知,,,,其中,,,即消去,可得反解,即可求得,也可以通过书上3-23式求得通过正弦定理可求得继续,我们来看看角速度关系对于加速度,有如下关系其中现在,只需将所求得的,,和,,关联起来这是同一根杆,,,现在来看,,,由题目得,,和是未知的,但不影响整体,不然给一个初值,,当然,这是可以随意更改的。
基于以上的基本原理,matlab R2012b程序如下syms theta theta1 theta2 lamuda lamuda1 lamuda2 sigma sigma1 sigma2 beta beta1 beta2 l1 l11 l2 l21 t output itheta1=10;theta2=0;i=0;for theta3=60:420theta=theta3/180*pi;beta=asin((100/200)*sin(theta))+theta;l1=0.2*sin(beta)/sin(theta);beta1=(-theta1*(l1*sin(theta))*sin(theta)+theta1*(l1*cos(theta))*cos(theta))/(0.2*(sin(theta)*sin(b eta)+cos(theta)*cos(beta)));l11=-(theta1*(l1*sin(theta))*l1*cos(beta)+theta1*(l1*cos(theta))*l1*sin(beta))/(0.2*(sin(theta)*si n(beta)+cos(theta)*cos(beta)));C=(theta1^2)*0.2*cos(beta)-theta2*l1*sin(theta)-(theta1^2)*l1*cos(theta)-2*l11*theta1*sin(theta) ;D=(theta1^2)*0.2*cos(beta)+theta2*l1*sin(theta)-(theta1^2)*l1*cos(theta)+2*l11*theta1*sin(thet a);beta2=(-C*sin(theta)+D*cos(theta))/(0.2*(sin(theta)*sin(beta)+cos(theta)*cos(beta)));lamuda=beta-pi/2;lamuda1=beta1;lamuda2=beta2;sigma=asin((100/200)*sin(lamuda))+lamuda;l2=0.2*sin(sigma)/sin(lamuda);sigma1=(-lamuda1*(l2*sin(lamuda))*sin(lamuda)+lamuda1*(l2*cos(lamuda))*cos(lamuda))/(0.2 *(sin(lamuda)*sin(sigma)+cos(lamuda)*cos(sigma)));l21=-(lamuda1*(l2*sin(lamuda))*l2*cos(sigma)+lamuda1*(l2*cos(lamuda))*l2*sin(sigma))/(0.2* (sin(lamuda)*sin(sigma)+cos(lamuda)*cos(sigma)));A=(lamuda1^2)*0.2*cos(sigma)-lamuda2*l2*sin(lamuda)-(lamuda1^2)*l2*cos(lamuda)-2*l21*la muda1*sin(lamuda);B=(lamuda1^2)*0.2*cos(sigma)+lamuda2*l2*sin(lamuda)-(lamuda1^2)*l2*cos(lamuda)+2*l21*l amuda1*sin(lamuda);sigma2=(-A*sin(lamuda)+B*cos(lamuda))/(0.2*(sin(lamuda)*sin(sigma)+cos(lamuda)*cos(sigma )));i=i+1;output(i,1)=fix(theta/pi*180);output(i,2)=fix(sigma/pi*180);output(i,3)=fix(sigma1);output(i,4)=fix(sigma2);endoutputa=output(:,1);b=output(:,2);c=output(:,3);d=output(:,4);h1=plot(a,b);hold on;h2=plot(a,c);hold on;h3=plot(a,d);hold on;set(h1,'color',[1 0 0],'linewidth',2);set(h2,'color',[0 1 1],'linewidth',1);set(h3,'color',[0 0 1],'linewidth',2);m=legend('角位移','角速度','角加速度');x label('θ');title('平面连杆机构运动分析');figure;h1=plot(a,b);hold on;x label('θ');ylabel('角位移');title('平面连杆机构运动角度——角位移图');figure;h2=plot(a,c);hold on;x label('θ');ylabel('角速度');title('平面连杆机构运动角度——角速度图'); figure;h3=plot(a,d);hold on;x label('θ');ylabel('角加速度');title('平面连杆机构运动角度——角加速度图');汇总图各自的图像结果分析,上面的图形只是在一个初值,的条件下得出的,为了能解决所有问题,修改程序如下syms theta theta1 theta2 lamuda lamuda1 lamuda2 sigma sigma1 sigma2 beta beta1 beta2 l1 l11 l2 l21 t output iprompt={'输入:', '输入' ,'输入' };%设置提示字符串name='输入初值';%设置标题 numlines=1;%指定输入数据的行数 defAns={'60','10','0'};%设定默认值 Resize='on';%设定对话框尺寸可调节answer=inputdlg(prompt,name,numlines,defAns,'on');%创建输入对话框 h= str2num(answer{1}); theta1= str2num(answer{2}); theta2= str2num(answer{3}); i=0;for theta3=h:(360+h) theta=theta3/180*pi;beta=asin((100/200)*sin(theta))+theta; l1=0.2*sin(beta)/sin(theta);beta1=(-theta1*(l1*sin(theta))*sin(theta)+theta1*(l1*cos(theta))*cos(theta))/(0.2*(sin(theta)*sin(b eta)+cos(theta)*cos(beta)));l11=-(theta1*(l1*sin(theta))*l1*cos(beta)+theta1*(l1*cos(theta))*l1*sin(beta))/(0.2*(sin(theta)*si n(beta)+cos(theta)*cos(beta)));C=(theta1^2)*0.2*cos(beta)-theta2*l1*sin(theta)-(theta1^2)*l1*cos(theta)-2*l11*theta1*sin(theta) ;D=(theta1^2)*0.2*cos(beta)+theta2*l1*sin(theta)-(theta1^2)*l1*cos(theta)+2*l11*theta1*sin(thet a);beta2=(-C*sin(theta)+D*cos(theta))/(0.2*(sin(theta)*sin(beta)+cos(theta)*cos(beta)));lamuda=beta-pi/2;lamuda1=beta1;lamuda2=beta2;sigma=asin((100/200)*sin(lamuda))+lamuda;l2=0.2*sin(sigma)/sin(lamuda);sigma1=(-lamuda1*(l2*sin(lamuda))*sin(lamuda)+lamuda1*(l2*cos(lamuda))*cos(lamuda))/(0.2 *(sin(lamuda)*sin(sigma)+cos(lamuda)*cos(sigma)));l21=-(lamuda1*(l2*sin(lamuda))*l2*cos(sigma)+lamuda1*(l2*cos(lamuda))*l2*sin(sigma))/(0.2* (sin(lamuda)*sin(sigma)+cos(lamuda)*cos(sigma)));A=(lamuda1^2)*0.2*cos(sigma)-lamuda2*l2*sin(lamuda)-(lamuda1^2)*l2*cos(lamuda)-2*l21*la muda1*sin(lamuda);B=(lamuda1^2)*0.2*cos(sigma)+lamuda2*l2*sin(lamuda)-(lamuda1^2)*l2*cos(lamuda)+2*l21*l amuda1*sin(lamuda);sigma2=(-A*sin(lamuda)+B*cos(lamuda))/(0.2*(sin(lamuda)*sin(sigma)+cos(lamuda)*cos(sigma )));i=i+1;output(i,1)=fix(theta/pi*180);output(i,2)=fix(sigma/pi*180);output(i,3)=fix(sigma1);output(i,4)=fix(sigma2);endoutputa=output(:,1);b=output(:,2);c=output(:,3);d=output(:,4);h1=plot(a,b);hold on;h2=plot(a,c);hold on;h3=plot(a,d);hold on;set(h1,'color',[1 0 0],'linewidth',2);set(h2,'color',[0 1 1],'linewidth',1);set(h3,'color',[0 0 1],'linewidth',2);m=legend('角位移','角速度','角加速度');x label('θ');title('平面连杆机构运动分析');figure;h1=plot(a,b);hold on;xlabel('θ');y label('角位移');title('平面连杆机构运动角度——角位移图');figure;h2=plot(a,c);hold on;xlabel('θ');y label('角速度');title('平面连杆机构运动角度——角速度图');figure;h3=plot(a,d);hol d on;xlabel('θ');y label('角加速度');title('平面连杆机构运动角度——角加速度图');这样,在运行程序时就会弹出一个如下图所示的对话框,可以任意给定初值,解决不同问题。

Harbin Institute of Technology机械原理大作业(一)课程名称:机械原理设计题目:连杆机构设计28院系:班级:设计者:学号:指导教师:丁刚陈明设计时间:2014年6月哈尔滨工业大学能源科学与工程学院一.题目(1-28)如图所示机构,已知机构各构件的尺寸为AB=61mm,EF=132mm,BC=CE=CD=200mm,FG=160mm,AD=152mm,AG=472mm,DG=332mm,114β=︒,构建1的角速度为110/ rad sω=,试求构件2上点E的轨迹及构件5的角位移、角速度和角加速度,并对计算结果进行分析。
二.连杆机构结构分析该机构由包括机架在内的6个构件组成的,各构件之间运动约束都是转动副,其中,杆1为机构的原动件,杆2、3、4、5为从动件。
杆2和杆3组成了1个RRR型Ⅱ级基本杆组,杆4和杆5组成了1个RRR型Ⅱ级基本杆组。
图1 原动件图 2 RRR型II级杆组图表 1 RRR型II级杆组三.组成机构各基本杆组的运动分析数学模型1.原动件杆1的数学模型图 4 原动件杆11) 位置分析 ⎩⎨⎧+=+=ii A B ii A B l y y l x x ϕϕsin cos 2) 速度和加速度分析将上式对时间t 求导,可得速度方程: ⎪⎪⎩⎪⎪⎨⎧+==-==i i A B B i i A B Bl y y dt dy l x x dtdx ϕϕϕϕcos cos 将上式对时间t 求导,可得加速度方程: ⎪⎪⎩⎪⎪⎨⎧+-==--==i i i i i i A B B i i i i i iA B B l l y y dt y d l l x x dt x d ϕϕϕϕϕϕϕϕcos sin sin cos 222222 (2) RRR Ⅱ级杆组的运动分析如下图所示,当已知RRR 杆组中两杆长l i 、l j 和两外副B 、D 的位置和运动时,求内副C 的位置及运动以及两杆的角位置、角运动。

连杆机构设计1设计题目(9)在图1-9所示的机构中,已知l AB=60mm,lBC=180mm,lDE=200m m,l CD=120mm,lEF=300mm,h=80mm,h1=85mm,h2=225mm,构件1以等角速度w1=100rad/s转动。
求在一个运动循环中,滑块5的位移、速度和加速度曲线。
2对机构进行结构分析,找出基本杆组①AB即杆件1为原动件②DECB即杆件2、3为RRR型II级杆组③其中CE为同一构件上点,④EF和滑块即4、5为RRP型II级杆组3各基本杆组的运动分析数学模型② RRR 杆组运动分析的数学模型1.位置分析设两个构件长度1R ,2R 及外运动副1N ,2N 的位置已知,求两个构件的位置角1θ,2θ及内运动副3N 的位置。
选定坐标系及相应的标号如下图,构件的位置角i θ约定从响应构件的外运动副i N 引x 轴的方向线,按逆时针量取。
设外运动副1N ,2N 的位置坐标分别为1N (1x P ,1y P ),2N (2x P ,2y P ),则 12221212[( -)( -)]x x y y d P P P P =+ 222121cos ()/(2 )d R R R d α=++ 212 1arctan(( )/( )y y x x P P P P ϕ=-- 1θϕα=±内运动副3N 点坐标为:3111 cos x x P P R θ=+3111 sin y y P P R θ=+构件2K 的位置角:23232arctan[()/( )]y y x x P P P P θ=--位置分析过程中应注意两个问题:(1) 因为1N ,2N 的位置及杆长1R ,2R 都是给定的,这就可能出现d >12R R +或12d R R <-的情况。
在这两种情况下实际上不可能形成RRR 杆组,计算过程中应及时验算上述条件,如满足上述条件应中止运算并给出相应信息。
(2)在给定1N ,2N ,1R ,2R 的条件下,3N 可能有两个位置如上图中的3N 和3N ',相应的1θϕα=+和1θϕα'=-,我们称为杆组的两种工作状态。

哈工大机械原理大作业-连杆连杆是机械原理中常见的机构之一,也是机械工程中非常重要的部件。
它由两个旋转接头和一个连接两个旋转接头的杆件组成。
连杆广泛应用于各种机械设备中,如汽车发动机、泵、机床等。
本文将介绍连杆的工作原理、应用以及设计要点。
连杆的工作原理是将旋转运动转化为直线运动或将直线运动转化为旋转运动。
它通过两个旋转接头的运动将杆件上的一个点的运动转化为另一个点的运动。
连杆的运动有两种基本形式:一是曲柄连杆机构,二是摇杆连杆机构。
曲柄连杆机构中,一个旋转接头为曲柄,另一个旋转接头为连杆;摇杆连杆机构中,一个旋转接头为摇杆,另一个旋转接头为连杆。
连杆广泛应用于各种机械设备中。
在汽车发动机中,连杆将曲轴的旋转运动转化为活塞的直线运动,从而驱动汽缸的工作;在泵中,连杆将电机的旋转运动转化为柱塞的直线运动,从而产生压力;在机床中,连杆将电机的旋转运动转化为工作台的直线运动,从而实现加工。
设计连杆时需要考虑一些要点。
首先是连杆的材料选择和尺寸设计。
连杆需要承受较大的力和扭矩,因此需要选择具有较高强度和刚度的材料。
同时,根据应用需求和力学原理,设计连杆的尺寸,以确保其能够承受正常工作条件下的负荷。
其次是连杆的润滑和密封。
连杆在工作过程中需要润滑剂来减少摩擦和磨损,同时需要密封装置来防止润滑剂泄漏。
因此,设计连杆时需要考虑润滑剂的供给和密封装置的设计。
最后是连杆的制造和装配。
连杆的制造需要保证其精度和质量,以确保其运转平稳和可靠。
在装配过程中,需要按照设计要求进行装配,同时进行必要的调试和检测,以确保连杆的工作性能符合要求。
总之,连杆是机械工程中非常重要的部件,广泛应用于各种机械设备中。
设计和制造连杆需要考虑材料选择、尺寸设计、润滑和密封以及制造和装配等方面的要点。
通过合理的设计和制造,可以确保连杆的工作性能和可靠性,从而提高机械设备的工作效率和寿命。

机械原理大作业(一)作业名称:连杆机构运动分析设计题目: 20院系:英才学院班级: XXXXXXX设计者:邵广斌学号: XXXXXXXXXX指导教师:林琳设计时间: 2013年05月19日哈尔滨工业大学机械设计1.运动分析题目如图所示机构,已知机构各构件的尺寸为150AB mm =,97β=︒,400BC mm =,300CD mm =,320AD mm =,100BE mm =,230EF mm =,400FG mm =,构件1的角速度为110/rad s ω=,试求构件2上点F 的轨迹及构件5上点G 的位移、速度和加速度,并对计算结果进行分析。
2. 机构分析该机构由原动件AB (Ⅰ级杆组)、BCD (RRR Ⅱ级杆组)和FG (RRP Ⅱ级杆组)组成。
3. 建立坐标系如图3,建立以定点A 为原点的平面直角坐标系A-xy 。
图1 运动机构结构图4. 运动分析数学模型4.1 原动件AB原动件AB 的转角: 10~2ψπ= 原动件AB 的角速度:110/rad s ω=原动件AB 的角加速度: 10α= 运动副A 的位置坐标: 0A x = 0A y =运动副A 的速度: 0xA v = 0yA v = 运动副A 的加速度: 0xA a = 0yA a =原动件AB 长度:150AB l mm =运动副B 的位置坐标: 1B A AB x x l cos ψ=+1B A AB y x l sin ψ=+运动副B 的速度: 11 xB xA AB v v l sin ωψ=-11 yB yA AB v v l cos ωψ=+运动副B 的加速度: 2 1111 xBxA AB AB a a l cos l sin ωψαψ=--21111yB yA AB AB a a l sin l cos ωψαψ=-+4.2 RRR Ⅱ级杆组BCD运动副D 的位置坐标: 320D x mm = 0D y = 运动副D 的速度: 0xD v = 0yD v = 运动副D 的加速度: 0xD a = 0yD a = 杆BC 长度: 400BC l mm = 杆CD 长度:300CD l mm =BC 相对于x 轴转角:200ψ=其中02BC D B A l x x =-() 0 2 BC D B B l y y =-()2220B B C C l C l D l D =+- 222())(BDD B D B l x x y y =-+- CD 相对于x 轴转角: 3C DC Dy y arctanx x ψ-=-求导可得BC 角速度2ω、角加速度2α以及CD 角速度3ω、角加速度3α。

机械设计基础大作业计算说明书题目:平面连杆机构设计学院:材料学院班号:学号:姓名:日期:2014年9月30日哈尔滨工业大学机械设计基础大作业任务书题目:平面连杆机构设计设计原始数据及要求:3l (mm )=6030ψ=︒1.2K = 60CDA ∠=︒目录1设计题目 (1)2设计原始数据 (1)3设计计算说明书 (1)3.1计算极位夹角θ (1)3.2设计制图 (1)γ (2)3.3验算最小传动角4参考文献 (2)1 设计题目平面连杆机构的图解法设计2 设计原始数据设计一曲柄摇杆机构。
已知摇杆长度3l ,摆角ψ ,摇杆的行程速比系数K ,要求摇杆CD 靠近曲柄回转中心A 一侧的极限位置与机架间的夹角为CDA ∠ ,试用图解法设其余三杆的长度,并检验(测量或计算)机构的最小传动角γ 。
3l (mm )=60 30ψ=︒1.2K = 60CDA ∠=︒3 设计计算说明书3.1 计算极位夹角θ 极位夹角11801K K θ-=︒+ 代入数值 1.211800.09118016.41.21θ-=︒=︒=︒+ 3.2 设计制图3.2.1 在图纸上取一点作为D 点,从D 点垂直向上引出一条长为60mm 的线段,终点为2C ;3.2.2 从D 点在2C D 左侧引出一条与2C D 夹角为30︒的射线;3.2.3 以D 点为圆心,以2C D 为半径画圆,与射线交于点1C ;3.2.4 分别从1C 、2C 两点向下引两条射线,射线与12C C 夹角为73.6︒,两射线交于O 点,O 点即为曲柄的回转中心;3.2.5 以O 点为圆心以1OC 为半径画圆;3.2.6 过点D 向左侧引出一条射线,射线与1C D 夹角60︒,与圆交于点A ;3.2.7 连接1AC ,2AC 并量取其长度,以12||AC AC l l - 为半径画圆,直线1AC ,2AC 与圆的交点分别为1B ,2B ;3.2.8 在图中量取112AB mm =,1170B C mm = ,57AD mm =3.3 验算最小传动角γ3.3.1 在1C 处根据余弦定理2222221111586057cos 0.534225860AC C D AD AC C D γ+-+-=== 57.7γ=︒3.3.2 在2C 处根据余弦定理2222222222826057cos 0.722228257AC C D AD AC C D γ+-+-=== 43.8γ=︒所以最小传动角43.8γ=︒4 参考文献[1]宋宝玉,王瑜,张锋主编.机械设计基础.哈尔滨:哈尔滨工业大学出版,2010.[2]王瑜主编.机械设计基础大作业指导书.哈尔滨:哈尔滨工业大学出版社,2014.。

机械原理大作业课程名称:机械原理设计题目:机械原理大作业院系:汽车工程学院车辆工程班级:1101201姓名:。
学号:。
指导教师:游斌弟大作业1 连杆机构运动分析1、运动分析题目如图所示机构,已知机构各构件的尺寸为280mm AB =,350mm BC =,320mm CD =,160mm AD =,175mm BE = 220mm EF =,25mm G x =,80mm G y =,构件1的角速度为110rad/s ω=,试求构件2上点F 的轨迹及构件5的角位移、角速度和角加速度,并对计算结果进行分析。
图 12、对机构进行结构分析该机构由I 级杆组RR (原动件1)、II 级杆组RRR (杆2、杆3)和II 级杆组RPR (滑块4及杆5)组成。
I 级杆组RR ,如图2所示;II 级杆组RRR ,如图3所示;II 级杆组RPR ,如图4所示。
图2 图 2图4 3、建立坐标系建立以点A为原点的固定平面直角坐标系4、各基本杆组运动分析的数学模型(1)同一构件上点的运动分析:如图5所示的构件AB,,已知杆AB 的角速度=10/rad s ω,AB 杆长i l =280mm,可求得B 点的位置B x 、B y ,速度xB v 、yB v ,加速度xB a 、yB a 。
=cos =280cos B i x l ϕϕ; =sin =280sin B i y l ϕϕ;图 3==-sin =-BxB i B dx v l y dt ωϕω; ==cos =;B yB i B dyv l x dt ωϕω222B 2==-cos =-BxB i d x a l x dt ωϕω;2222==-sin =-ByB i Bd y a l y dtωϕω。
图 4(2)RRRII 级杆组的运动分析如图6所示是由三个回转副和两个构件组成的II 级组。
已知两杆的杆长2l 、3l 和两个外运动副B 、D 的位置(B x 、B y 、D x 、D y )、速度( xB yB xD yD v v v v 、、、 ) 图6和加速度(xB yB xD yD a a a a 、、、)。

H a r b i n I n s t i t u t e o f T e c h n o l o g y连杆机构设计设计说明书课程名称:机械原理设计题目:连杆机构设计院系:班级:设计者:学号:指导教师:哈尔滨工业大学大作业1 连杆机构运动分析25题:如图1-25所示机构,已知机构各构件的尺寸为齿轮1,齿轮2,齿轮5的齿数分为z1=17,z2=z5=40,BC=70mm,CD=270mm,EF=80mm,DE=240mm,DG=500mm,h=160mm,齿轮1的角速度为w1=10rad/s,试求点D的轨迹及构件7上点G的位移,速度和加速度,并对计算结果进行分析。
一.机构分析:考虑到BC杆和EF杆的长及齿轮间的传动,取齿轮模数为6,BF间的距离为300mm,由此可确定AB上述机构可简化为下图中所示机构,其中BC和EF杆的角速度相等(大小相同,方向相同),所以该机构只有一个自由度。
建立如图所示的坐标系:该机构可划分为以下几个基本杆组:RRRRRRRP二.各杆组的运动分析数学模型:(1)RR:已知A点的坐标,速度,加速度和AB杆的距离l i,求B点的运动量。
位置:x B=x A+l i cosφi ; y B=x A+l i cosφi速度和加速度:dx B dt =ẋA−φil i sinφi;dx Bdt=ẋA−φil i sinφi;d2x B dt2=ẍA−φi2l i cosφi−φil i sinφi;d2x B dt2=ÿA−φi2l i sinφi+φil i cosφi(2)RRR:已知两杆杆长和两个外运动副B,D的位置,速度和加速度。
求运动副C的运动量和两杆的角位置,角速度和角加速度。
由x c=x B+l i cosφi =x D+l j cosφj; (1)y c=y B+l i sinφi =y D+l j sinφj;(2)可得φi =2arctan B0±√A20+B20−C20A0+C0(B0=2l i(y D−y B),C0=l i2+l BD2−l j2) (B,C,D逆时针排列时取负号,反之取正号)由此可求得x c,y c,之后可以得到φj。
哈工大机械原理大作业连杆Modified by JACK on the afternoon of December 26, 2020Harbin Institute of Technology机械原理大作业一课程名称:机械原理设计题目:连杆机构运动分析院系:机电工程学院班级:设计者:学号:指导教师:设计时间:1.运动分析题目(11)在图所示的六杆机构中,已知:AB l =150mm, AC l =550mm, BD l =80mm, DE l =500mm,曲柄以等角速度1w =10rad/s 沿逆时针方向回转,求构件3的角速度、角加速度和构件5的位移、速度、加速度。
2.机构的结构分析建立以点A 为原点的固定平面直角坐标系A-x, y,如下图:机构结构分析该机构由Ⅰ级杆组RR (原动件1)、Ⅱ级杆组RPR (杆2及滑块3)和Ⅱ级杆组RRP (杆4及滑块5)组成。
3.建立组成机构的各基本杆组的运动分析数学模型原动件1(Ⅰ级杆组RR )由图所示,原动件杆1的转角a=0-360°,角速度1w =10rad/s ,角加速度1a =0,运动副A 的位置坐标A x =A y =0,速度(A ,A),加速度(A ,A ),原动件1的长度AB l =150mm 。
求出运动副B 的位置坐标(B x , B y )、速度(B ,B )和加速度(B ,B )。
杆2、滑块3杆组(RPR Ⅱ级杆组)已出运动副B 的位置(B x , B y )、速度(B ,B )和加速度(B ,B ),已知运动副C 的位置坐标C x =0, C y =550mm,速度,加速度,杆长AC l =550mm 。
求出构件2的转角b,角速度2w 和角加速度2a . 构件二上点D 的运动已知运动副B 的位置(B x , B y )、速度(B ,B )、加速度(B ,B ),已经求出构件2的转角b ,角速度2w 和角加速度2a ,杆BD 的长度BD l =80mm 。
Harbin Institute of Technology(一)连杆设计说明书课程名称:机械原理设计题目:连杆机构运动分析院系:机电工程学院班级:1308302设计者:吉曾纬指导教师:赵永强唐德威设计时间:2015年6月运动分析题目:如图所示机构,已知机构各构件的尺寸为AB=150mm ,β=97°,BC=400mm ,CD=300mm ,AD=320mm ,BE=100mm ,EF=230mm ,FG=400mm ,构件1的角速度为ω1=10rad/s,试求构件2上点F 的轨迹及构件5上点G 的位移、速度和加速度,并对计算结果进行分析。
一.对机构进行结构分析依题意可以将杆机构看作曲柄滑块机构和曲柄摇杆机构。
对4机构进行结构分析该机构由原动件AB (Ⅰ级组),BCD (RRR Ⅱ级杆组)和FG (RRP Ⅱ级杆组)组成。
二.建立以点A 为原点的固定平面直角坐标系A-x,y,如图所示。
三.各基本杆组的运动分析数学模型(1)原动件AB(Ⅰ级组)已知原动件AB的转角ψ1=0~2π原动件AB的角速度ω1=10rad/s 原动件AB的角加速度α1=0运动副A的位置坐标xA =0 yA=0A点与机架相连,即该点速度和加速度均为0。
运动副A的速度vxA =0 vyA=0运动副A的加速度axA =0 ayA=0原动件AB长度lAB=150mm 可求出运动副B的位置坐标xB =xA+lABcosψ1yB=xA+lABsinψ1运动副B的速度vxB = vxA-ω1lABsinψ1vyB= vyA+ω1lABcosψ1运动副B的加速度a xB = axA-ω12 lABcosψ1-α1lABsinψ1ayB=ayA-ω12 lABsinψ1+α1lABcosψ1(2) BCD (RRR Ⅱ级杆组)由(1)知B 点位置坐标、速度、加速度 运动副D 点位置坐标x D =320mm y D =0 D 点与机架相连,即该点速度和加速度均为0。
连杆机构运动分析说明书院(系)机电工程学院专业机械设计制造及其自动化姓名李乾学号1130810904班号1308109指导教师唐德威、赵永强日期2015年6月20日哈尔滨工业大学机电工程学院2015年6月一、题目如图1所示机构,已知机构各构件的尺寸为l AB=200mm,l BD=700mm,l AC=400mm,l AE=800mm,构件1的角速度为ω1=10rad/s,试求构件2上点D的轨迹及构件5的角位移、角速度和角加速度,并对计算结果进行分析。
(题中构件尺寸满足l BD-l AB<l AE<l BD+l AB)。
图 1 机构运动简图二、建立数学模型分析1.建立坐标系建立以点A为原点的平面直角坐标系A-x,y,如图2所示图 2 建立坐标系2.对机构进行结构分析该机构由Ⅰ级机构AB、两个RPRⅡ级基本杆组BCD、ED组成。
杆组拆分结果如图3、图4、图5所示。
图 3 Ⅰ级杆组AB图 4 RPRⅡ级基本杆组BCD图 5 RPRⅡ级基本组DE3.确定已知参数和求解流程(1)原动件AB(I级杆组)已知原动件1的转角φ=0~360°运动副A的运动参数x A=0y A=0原动件AB的长度l AB = 200mm代入I级杆组子程序,得到运动副B的位置坐标(x B,y B)根据《机械原理》第三版书中第36页的公式推导可知:A,B两点坐标在x轴,y轴上投影,得方程x B = x A+l AB*cosφy B = y A+l AB*sinφ(2)BCD(RPR II级杆组)已知运动副B的位置坐标(x B,y B)运动副C的坐标位置:x C=l AC=400mmy C=0代入RPR II级杆组子程序,求出构件2上D点的位置坐标(x D,y D)根据《机械原理》第三版书中第339页的公式推导可知:当杆件处于图所示位置,即x B>x D并且y B≥y D时,l j杆角位移:φj=arctan B0s+A0C0 A0s−B0C0式中:A0=x B-x DB0=y B-y DC0=l i+l ks=√A02+B02−C02而当x B<x D并且y B≥y D时,φj=arctan B0s+A0C0A0s−B0C0+180o 当x B<x D并且y B<y D时,φj=arctan B0s+A0C0A0s−B0C0+180o 当x B>x D并且y B<y D时,φj=arctan B0s+A0C0A0s−B0C0+360o图 6 RPR II级杆组分析内移动副C的位置:x C=x B-l i sinφjy C=y B-l i cosφj导杆上E点的位置:x E=x C+(l j-s)cosφjy E=y C+(l j-s)sinφj(3)DE(RPR II级杆组)已知运动副D的位置坐标(x D,y D),运动副E的坐标:x E=l AE=800mmy E=0代入RPR II级杆组子程序,求出构件5的转角φ5。
[键入公司名称]机械原理课程设计[键入文档副标题]p[选取日期]设计题目连杆机构运动分析机电工程学院1008103班H100811109学号设计者王鹏[在此处键入文档的摘要。
摘要通常是对文档内容的简短总结。
在此处键入文档的摘要。
摘要通常是对文档内容的简短总结。
]1、运动分析题目(12)如图所示的六杆机构中,各构件的尺寸分别为:l AB=200mm ,l BC=500mm ,l CD=800mm ,x F= 400mm ,x D=350mm ,y D=350mm ,ω=100rad s⁄,求构件5上点F的位移,速度和加速度。
2、建立坐标系建立以点A为原点的固定平面直角系A−x,y3、对机构进行结构分析该机构由I级杆组RR(原动件1)、II级杆组RRR(杆2、杆3)和II级杆组PRP(滑块4及滑块5)组成。
I级杆组RR,如图2所示;II级杆组RRR,如图2所示;II级杆组PRP,如图3所示。
4、确定已知参数和求解流程图1所示,规定当φ=10° 时,F 点纵坐标为0 (1)如图2所示,已知原动件杆1的转角,φ=0~360° {x B =l AB ×cos φy B =l AB ×sin φ(2)如图3所示,已知B ,D 两点坐标分别为(x B ,y B )(x D ,y D )和 l BC l CD利用方程组{(x −x B )2+(y −y B )2=l BC 2(x −x D )2+(y −y D )2=l CD2 可以求解出C 点坐标(3)如图4所示,已知C 点坐标、x F 、x D 、y D利用几何关系可以求解出E 点坐标同时,当φ=10° 时,可以求出杆EF 长,记为 l EF进而,可以求出F 点坐标,即F 点位移(4)利用导数的定义与其物理意义v n =s n+h −s n−h2ha n =s n+h −2s n +s n−hh 2利用上述公式,选取适当的步长h ,利用F 点位移就可以得出速度与加速度5、用VC 编程#include <stdio.h>#include <math.h>#define pi 3.14159265358979323846//定义全局变量double Lab,Lbc,Lcd,Xf,Xd,Yd;//定义已知位置量double Wab;//定义角速度量//定义被调用函数void Ccorner (double *a,double *b,double c);//声明C点坐标函数求解函数void Pcorner (double *a,double *b,double c,double d,double e);//声明P点坐标函数求解函数double Kcd (double a,double b);//声明CD直线倾斜角求解函数//主函数main (){Lab=0.200;Lbc=0.500;Lcd=0.800;Xf=0.400;Xd=0.350;Yd=0.350;//赋位置量值Wab=100;//赋角速度值//未知几何与位置参量double Xb,Yb;//定义B点坐标double Xc,Yc;//定义C点坐标double Ye;//定义E点纵坐标double Xp,Yp;//定义瞬心p点坐标double Lef;//定义bp,cp,ef,bd杆长double Yf[720];//定义F点纵坐标//未知速度参量double Vf[720];//定义EF杆速度//未知加速度参量double Af[720];//定义加速度//其余参量double o=10*pi/180,k,k1;//主动杆角度变量与CD杆倾斜角double t=1*pi/180/100;//时间参量,用定义法求速度与加速度int i;//循环控制变量//主函数主体//求位移量for (i=0;i<=361;i++){//准备几何量Xb=Lab*cos(o), Yb=Lab*sin(o);Ccorner (&Xc,&Yc,o);//求C点坐标Pcorner (&Xp,&Yp,Xc,Yc,o);//求瞬心P点坐标k=Kcd (Xp,Yp);//求CD杆倾斜角//求解位移量(规定主动杆10度为Yf零点)if (i==0){k1=k;}Lef=tan(k1)*Xd+Yd;//ef杆长Ye=tan(k)*Xd+Yd;Yf[i]=Ye-Lef;o=o+1*pi/180;}//用定义求速度for (i=1;i<=361;i++){Vf[i]=(Yf[i+1]-Yf[i-1])/(2*t);}//用定义求加速度for (i=1;i<=361;i++){Af[i]=(Yf[i+1]-2*Yf[i]+Yf[i-1])/pow(t,2);}//输出语句for (i=1;i<=180;i++){printf ("%d,%lf,%lf,%lf,\t",i+10,Yf[i]*1000,Vf[i],Af[i]);printf ("%d,%lf,%lf,%lf\n",i+190,Yf[i+180]*1000,Vf[i+180],Af[i+180]); }}//C点坐标值函数void Ccorner(double *a,double *b,double c)//&Xc,&Yc,o{double i,j,x,y,z;//中间参数i=(pow(Lcd,2)-pow(Lbc,2)+pow(Lab*sin(c),2)-pow(Yd,2)+pow(Lab*cos(c),2)-pow((Xd+Xf),2))/(2*(Lab*cos(c)-Xd-Xf));j=(Lab*sin(c)-Yd)/(Lab*cos(c)-Xf-Xd);x=pow(j,2)+1;y=2*(Xf+Xd)*j-2*i*j-2*Yd;z=pow(i,2)-2*(Xf+Xd)*i+pow((Xf+Xd),2)+pow(Yd,2)-pow(Lcd,2);*b=(-y+sqrt(pow(y,2)-4*x*z))/(2*x);*a=i-j*(*b);}//求瞬心P点坐标函数void Pcorner(double *a,double *b,double c,double d,double e)//&Xp,&Yp,Xc,Xp,o{double a1,b1,c1,a2,b2,c2,i,j,k;//中间参量a1=tan(e),a2=(d-Yd)/(c-Xd-Xf);b1=b2=-1;c1=0,c2=(c*(d-Yd)/(c-Xd-Xf))-d;i=a1*b2-b1*a2;j=c1*b2-b1*c2;k=a1*c2-c1*a2;*a=j/i;*b=k/i;}//CD杆倾斜角double Kcd(double a,double b)//Xp,Yp{double k1;//中间参量k1=-atan ((b-Yd)/(a-Xd-Xf));return k1;}6、计算结果(程序计算结果附在图像之后)6.1位移、速度、加速度的图像点F的位移线图如图5所示。
连杆机构设计1设计题目(9)在图1-9所示的机构中,已知l AB=60mm,l BC=180mm,l DE=200mm,l CD=120mm,l EF=300mm,h=80mm,h1=85mm,h2=225mm,构件1以等角速度w1=100rad/s转动。
求在一个运动循环中,滑块5的位移、速度和加速度曲线。
2对机构进行结构分析,找出基本杆组①AB即杆件1为原动件②DECB即杆件2、3为RRR型II级杆组③其中CE为同一构件上点,④EF和滑块即4、5为RRP型II级杆组3各基本杆组的运动分析数学模型② RRR 杆组运动分析的数学模型1.位置分析设两个构件长度1R ,2R 及外运动副1N ,2N 的位置已知,求两个构件的位置角1θ,2θ及内运动副3N 的位置。
选定坐标系及相应的标号如下图,构件的位置角i θ约定从响应构件的外运动副i N 引x 轴的方向线,按逆时针量取。
设外运动副1N ,2N 的位置坐标分别为1N (1x P ,1y P ),2N (2x P ,2y P ),则 12221212[( -)( -)]x x y y d P P P P =+ 222121cos ()/(2 )d R R R d α=++ 212 1arctan(( )/( )y y x x P P P P ϕ=--1θϕα=±内运动副3N 点坐标为:3111 cos x x P P R θ=+3111 sin y y P P R θ=+构件2K 的位置角:23232arctan[()/( )]y y x x P P P P θ=--位置分析过程中应注意两个问题:(1)因为1N ,2N 的位置及杆长1R ,2R 都是给定的,这就可能出现d >12R R +或12d R R <-的情况。
在这两种情况下实际上不可能形成RRR 杆组,计算过程中应及时验算上述条件,如满足上述条件应中止运算并给出相应信息。
(2)在给定1N ,2N ,1R ,2R 的条件下,3N 可能有两个位置如上图中的3N 和3N ',相应的1θϕα=+和1θϕα'=-,我们称为杆组的两种工作状态。
对于实际构件而言,杆组只可能在一种工作状态下运动,而且在机构运动过程中只要不出现12d R R =±的情况(这种情况下,机构处于瞬时运动不确定状态,设计时应避免)杆组就不会从一种工作状态变为另一种工作状态,所以运动分析时可预先按机构的实际工作位置,指明杆组是哪一种工作状态。
约定状态参数M :123N N N 为逆时针读取时M =1,123N N N 为顺时钟时M =-1。
2.速度分析设外运动副1N ,2N 点的速度1x v ,1y v 及2x v ,2y v 已知,求3N 点的速度3x v ,3y v 及构件1K ,2K 的角速度1ω,2ω。
因为3111222 cos cos x x x P P R P R θθ=+=+2311122 sin sin y y y P P R P R θθ=+=+将上式对时间t 微分:311112222sin sin x x x v v R v R ωθωθ=-=-311112222cos cos y y y v v R v R ωθωθ=+=+注意到:11311131cos , sin x x y y R P P R P P θθ=-=-(1)22322232cos , sin x x y y R P P R P P θθ=-=-式(1)可写为21131322131322()()=( )()x x y y y y y y x x x x v v P P P P v v P P P P ωω----⎡⎤⎡⎤⎛⎫⎢⎥ ⎪⎢⎥----⎝⎭⎣⎦⎣⎦令:31323231Q=( )( )( )( )y y x x y y x x P P P P P P P P -----则:121322132[()( )()( )]/x x x x y y y y v v P P v v P P Q ω=---+--221312131[()( )()( )]/y y y y x x x x v v P P v v P P Q ω=---+--将1ω,2ω值代入式(1)即可求得3x v ,3y v 。
3.加速度分析设外运动副1N ,2N 点的加速度1122 ,,,x y x y a a a a 已知,求3N 点的加速度33,x y a a ,及构件12,K K 的角加速度12,εε。
将式(1)对时间t 微分得:1313231322()()=( )()A y y y y x x x x B E P P P P P P P P E εε---⎡⎤⎡⎤⎛⎫ ⎪⎢⎥⎢⎥---⎝⎭⎣⎦⎣⎦式中:21311322()()A x x y y y y E a a v v v v ωω=-+---21311322()()B y y x x x x E a a v v v v ωω=---+-13232 [( )( )]/A x x B y y E P P E P P Q ε=--+- 23131 [( )( )]/A x x B y y E P P E P P Q ε=--+- 内运动副3N 点的加速度33,x y a a 可由微分式(1)求得。
③ 平面运动构件(单杆)的运动分析已知构件K 上的1N 点的位置1x P ,1y P ,速度为1x v ,1Y v ,加速度为1 x a ,1y a 及过点的1N 点的线段12N N 的位置角θ,构件的角速度ω,角加速度ε,求构件上点2N 和任意指定点3N (位置参数13N N =2R ,213N N N ∠=γ)的位置、速度、加速度。
1N ,3N 点的位置为:211cos x x P P R θ=+211sin y y P P R θ=+312cos()x x P P R θγ=++312sin()y y P P R θγ=++ 1N ,3N 点的速度,加速度为:211211sin ()x x x y y v v R v P P ωθω=-=--211121sin (-) y y y x x v v R v P P ωθω=-=-312131sin() () x x x y y v v R v P P ωθγω=-+=--312131cos()()y y y x x v v R v P P ωθγω=-+=--2212121()()x x y y x x a a P P P P εω=----2212121()()y y x x y y a a P P P P εω=+---2313131()()x x y y x x a a P P P P εω=----23133(1)(1)y y x x y y a a P P P Pεω=+--- ④ RRP 杆组运动分析的数学模型1.位置分析设已知外运动副点1N 及移动副导路上任意一选定参考点2N 的位置,构件1K 的长度1R 及导路的位置角β,求构件1K 的位置角1θ及内运动副3N 点的位置(如右图)。
β角从水平线到23N N 度量。
1221212[()()]x x y y d P P P P =-+-1212arctan[()/ ()]y y x x P P P P ϕ=--由1N 向导路作垂线,垂足为A ,令1N A =u ,2N A =e ,3N A =f 则cos()e d ϕβ=-)sin(-)u d ϕβ=12221(-)f R u =3N 点相对于导路上参考点2N 的滑移距离:2R e f =±显然,当1||R u <时无解。
当1||R u >时有两个解,对应于杆组的不同位置状态。
若∠123N N N π≤2,则2R e f =+,约定状态参数M =1;若∠123N N N >2π,则2R e f '=-,则约定状态参数M =-1。
内运动副3N 的位置坐标: 322322cos , sin x x y y P P R P P R ββ=+=+构件1K 的位置角:13131arctan[(-)/ (-)]y y x x P P P P θ=2.速度分析1N ,2N 点的速度为1x v ,1y v 及2x v ,2y v 已知,导路的角速度βω,求构件K1的角速度1ω,点的速度3x v ,3y v 及3N 点相对于导路上重合点的相对速度构件2r v311122cos cos x x x P P R P R θβ=+=+311122sin sin y y y P P R P R θβ=+=+(2)上式对时间t 微分,可解出:11==(sin cos )/v v E F Q θωββ'-+223131[()()]/r v x x v y y R v E P P F P P Q '==--+-式中:212sin v x x E v v R βωβ=--212cos v y y F v v R βωβ=--3131()sin () cos y y x x Q P P P P ββ=-+-3N 点的速度为:31111sin x x v v R ωθ=-,31111cos y y v v R ωθ=+3.加速度分析1N ,2N 点的加速度1122 ,,,x y x y a a a a 及移动副导路的角加速度βε已知,求构件1K 的角加速度1ε,3N 点的加速度33,x y a a ,及3N 点相对于移动副导路上重合点的相对角速度2r a 。
对式(2)进行两次微分可得:1(sin cos )/A A E F Q εββ=-+23131(()())/r A x x A y y a E P P F P P Q =--+-式中:22211312232()cos 2sin ()A x x x x r y y E a a P P R v P P βββωωβωβε=-+-----222113112232()sin 2cos ()A y y y y r x x F a a P P R v P P ββωωβωβε=-+--+--3131()sin () cos y y x x Q P P P P ββ=-+-3N 点的加速度:231111111cos sin x x a a R R ωθεθ=--231111111sin cos y y a a R R ωθεθ=-+4建立坐标系,程序设计及画图以D 点为坐标原点,自然方向为坐标xy 轴(1)滑块5的位移曲线(使用matlab 编程画图,详见附录1)(2)滑块5的速度曲线(使用matlab编程画图,详见附录2)(3)滑块5的加速度曲线(使用matlab编程画图,详见附录3)附录附录1t=0:0.0002.*pi:0.04.*pi;xd=225+60.*cos(100.*t);yd=80+60.*sin(100.*t);A0=2.*120.*xd;B0=2.*120.*yd;C0=120.^2+xd.^2+yd.^2-180.^2;ai=2.*atan((B0+sqrt(A0.^2+B0.^2-C0.^2))./(A0+C0)); xe=200.*cos(ai);ye=200.*sin(ai);xf=xe-sqrt(300.^2-(165-ye).^2);plot(t,xf)附录2t=0:0.0002.*pi:0.04.*pi;xd=225+60.*cos(100.*t);yd=80+60.*sin(100.*t);A0=2.*120.*xd;B0=2.*120.*yd;C0=120.^2+xd.^2+yd.^2-180.^2;ai=2.*atan((B0+sqrt(A0.^2+B0.^2-C0.^2))./(A0+C0)); xe=200.*cos(ai);ye=200.*sin(ai);xf=xe-sqrt(300.^2-(165-ye).^2);vf=diff(xf);t=0:0.0002.*pi:(0.04-0.0002).*pi;plot(t,vf);附录3t=0:0.0002.*pi:0.04.*pi;xd=225+60.*cos(100.*t);yd=80+60.*sin(100.*t);A0=2.*120.*xd;B0=2.*120.*yd;C0=120.^2+xd.^2+yd.^2-180.^2;ai=2.*atan((B0+sqrt(A0.^2+B0.^2-C0.^2))./(A0+C0)); xe=200.*cos(ai);ye=200.*sin(ai);xf=xe-sqrt(300.^2-(165-ye).^2);af=diff(diff(xf));t=0:0.0002.*pi:(0.04-0.0004).*pi;plot(t,af)。