下载文档原格式
机械原理平面连杆机构及设计平面连杆机构是机械原理中最经典也是最重要的一种机构类型之一。
这种机构由多个刚性杆件组成，每个杆件都能在平面内移动，它们通过连接点（铰链/球头）相互连接。
平面连杆机构在机械工程领域中有着广泛的应用，能够实现很多不同的机械运动和工作原理。
平面连杆机构中最重要的构件是连杆，也就是连接各个零件的关键杆件，如果连杆设计不合适可能导致机构性能的下降。
因此，平面连杆机构的设计要受到重视，需要考虑以下几个因素。
一、长度比例连杆不同长度比例的设置，对整个机构的运动特性和反应速度有着很大的影响。
在设计平面连杆机构时，需要根据机构所要完成的任务，选择恰当的连杆长度比例，保证机构的平衡性和可靠性，以及使机构的工作效率更高。
二、铰链/球头的位置铰链/球头是平面连杆机构中的关键组成部分。
在设计平面连杆机构时，需要合理选择铰链/球头的位置，以达到机构所要完成的特定任务。
如果铰链/球头设置不当，或者位置过分集中，会使机构不平衡或失效。
因此，设计者需要考虑连杆的长度、位置、形状和角度等因素。
三、材质选择平面连杆机构的设计材料非常重要，它将直接影响到机构的质量和强度。
不同材料的连接部分，对于平面连杆机构的工作效率和稳定性有着非凡的意义。
因此，在设计时，应本着安全、可靠、实用的原则，选用优质、耐用的材料，确保机构长期稳定、可靠的工作。
以汽车减震器为例，汽车减震器中使用的是多连杆机构原理，作为一种基于平面连杆机构的机构类型，它通过几个连杆的特定结构和布局，使得整个减震器能够更好地适应路况，缓解车辆的震动和冲击。
汽车减震器的设计考虑了多个因素，包括结构的稳定性和可靠性，杆件的材质和尺寸比例等。
总结来说，平面连杆机构是机械原理中非常重要的一种机构类型，广泛应用于机械和工程领域，需要经过仔细的设计和考虑，才能达到最好的运转效果。
设计者需要从多个维度进行考虑，包括长度比例、铰链/球头的位置、材质选择等等。
这些因素的合理应用，能够使平面连杆机构能够更好地适应不同的任务需求，达到最高的技术性能和质量水平。
机械原理平面连杆机构及设计平面连杆机构是一种最为基本的机械结构，由于其结构简单、运动可靠等特点，被广泛应用于各种机械设备中。
本文将对平面连杆机构进行介绍，并探讨其设计原理。
平面连杆机构是由至少一个定点和至少三个连杆组成的机构。
定点为固定参考点，连杆是由铰链连接的刚性杆件。
连杆可以分为连杆和曲柄，连杆连接在定点上，曲柄则旋转。
平面连杆机构的运动由这些连杆的位置和相互连接方式决定。
平面连杆机构的设计原理基于以下几个方面：1.运动分析：在设计平面连杆机构之前，首先需要进行运动分析，确定所需的运动类型。
运动类型可以是旋转、平移、摆动、滑动等。
通过运动分析，可以确定连杆的长度和相互连接的方式。
2.运动性能：平面连杆机构的优点是运动可靠，但运动性能也是需要考虑的重要因素。
例如，设计中需要考虑速度、加速度、力和力矩等参数，以满足机构的运动要求。
3.静力学分析：平面连杆机构在工作过程中可能会受到外力的作用，因此需要进行静力学分析。
静力学分析可以确定机构的力矩和应力，从而确定设计的合理性。
4.运动合成：在进行平面连杆机构的设计过程中，需要进行连杆的运动合成。
运动合成是指通过选择适当的连杆长度和连接方式，实现所需的运动类型。
5.运动分解：运动分解是指将合成的运动分解为各个连杆的运动。
通过运动分解，可以确定每个连杆的运动规律，从而进行设计。
当以上原理得到了充分的了解和运用后，可以进行平面连杆机构的具体设计。
具体的设计包括以下几个步骤：1.确定所需的运动类型：根据机械设备的需求，确定所需的运动类型，例如旋转、平移、摆动等。
2.运动分析：对机构进行运动分析，确定连杆的位置和连接方式。
根据机构的运动要求和外力作用，确定连杆的长度。
3.动力学分析：进行动力学分析，确定机构运动时的力学参数，如速度、加速度、力和力矩等。
4.运动合成与分解：根据所需的运动类型，进行运动合成和分解，确定连杆的运动规律。
5.结构设计：根据上述分析和计算结果，进行结构设计。
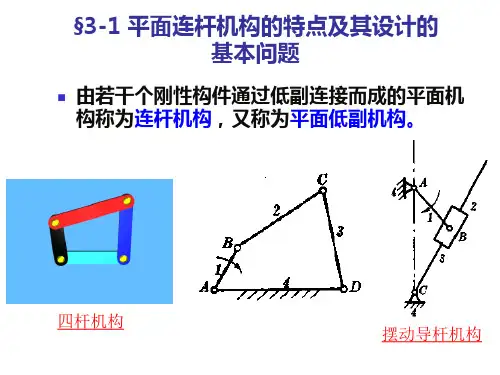
机械原理--平面连杆机构练习+答案《机械设计基础》作业二--平面连杆机构姓名班级学号成绩一、填空题：（24分）1、平面连杆机构，至少需要 4个构件。
2、平面连杆机构是由一些刚性构件用转动副和移动副连接组成的。
3、在铰链四杆机构中，运动副全部是转动副。
4、在铰链四杆机构中，能作整周连续回转的连架杆称为曲柄。
5、某些平面连杆机构具有急回特性。
从动件的急回性质一般用行程速度变化系数表示。
6、对心曲柄滑快机构无（有，无）急回特性；若以滑块为机架，则将演化成移动导杆机构。
7、铰链四杆机构根据有无曲柄分为曲柄摇杆机构、双曲柄机构和双摇杆机构。
如图所示铰链四杆机构中，若机构以AB为机架时，则为双曲柄机构；以BC杆为机架时，它为曲柄摇杆机构；以CD杆为机架时，它为双摇杆机构；而以AD杆为机架时，它为曲柄摇杆机构。
8、在曲柄摇杆机构中，当曲柄与机架两次共线位置时出现最小传动角。
9、压力角指：从动件上作用的力F 与该力作用点的速度（绝对速度）方向所夹的锐角α。
10、机构的压力角越小（大，小）对传动越有利。
11、运动副中，平面接触的当量摩擦系数为 f ，槽面接触的当量摩擦系数为f/sinθ，圆柱面接触的当量摩擦系数为ρ/r 。
12、移动副的自锁条件是驱动力F 与法向反力N的夹角β小于摩擦角ϕ，即驱动力作用在摩擦角之内，转动副的自锁条件是驱动力作用在摩擦圆之内，即e<ρ，其中e为驱动力臂长，螺旋副的自锁条件是螺纹升角α小于或等于螺旋副的摩擦角或当量摩擦角，即α≤ϕ。
二、选择题（27分）1、当四杆机构处于死点位置时，机构的压力角____B____。
A.为0ºB.为90ºC.与构件尺寸有关2、四杆机构的急回特性是针对主动件作___A_____而言的。
A. 等速转动B. 等速移动C. 变速转动或变速移动3、对于双摇杆机构，最短构件与最长构件长度之和____B____大于其它两构件长度之和。
A . 一定 B. 不一定 C. 一定不4、曲柄摇杆机构___B_____存在急回特性。
机械原理课程作业（一）平面连杆机构的运动分析(题号：1-A )班级 03021101学号姓名成绩同组者完成日期 2014年1月1日目录一．题目及原始数据 (3)二．平面连杆机构运动分析方程 (4)三．计算程序框图 (6)四．计算源程序 (7)五．计算结果 (13)六．运动线图分析 (17)七．运动线图分析 (19)八．体会及建议 (20)九．参考书目 (20)一． 题目及原始数据1.如图1所示平面六杆机构，试用计算机完成其运动分析。
图1设已知各构件的尺寸如表1所示，又已知原动件1以等角速度沿逆时针方向回转，试求各从动件的角位移、角速度、角加速度以及E 点的位移、速度、加速度的变化情况。
已知其尺寸参数如下表所示：表1 平面六杆机构尺寸参数 （） mm2、题目要求与成员组成及分工： （1）题目要求：三人一组计算出原动件从0到360时（计算点数N=37）所要求的各运动变量的大小，并绘出运动曲线图及轨迹曲线,本组选取题号为：1—A ，1—B,1-C 组。
(2)分工比例：学号 姓名 分工2011300652 张正栋 报告书写，制图、程序2011300620 肖川 制图 2011300622尹志成方程推导组号1ll 2 l 3 l 4 l 5 l 6αABC2-A2-B 3-C26.5 67.5 87.5 52.4 43600l2=116.6l2=111.6l2=126.6二． 平面连杆机构运动分析方程1. 位置方程在图1的直角坐标系中，建立该六杆机构的封闭矢量方程：将上式写成在两坐标轴上的投影式，并改写成方程左边尽含未知量的形式，即得1122334112233'1122226655'1122226655cos cos cos sin sin sin cos cos cos()cos cos sin sin sin()sin sin G G L L L L L L L L L L x L L L L L y L L θθθθθθθθπαθθθθθπαθθθ⎧⋅+⋅=⋅+⎪⋅+⋅=⋅⎪⎨⋅+⋅-⋅-+=-⋅-⋅⎪⎪⋅+⋅-⋅-+=-⋅-⋅⎩将上式化简可得：2233411223311'222255664'22225566cos cos cos sin sin sin cos cos()cos cos sin sin()sin sin G GL L L L L L L L L L L x L L L L L y θθθθθθθθαθθθθαθθ⎧⋅-⋅=-⋅⎪⋅-⋅=-⋅⎪⎨⋅+⋅-+⋅+⋅=-⎪⎪⋅+⋅-+⋅+⋅=⎩ 由以上各式即可得。
2. 速度方程根据A ω=ω1B ，可得222333111222333111'222222555666'222222555666sin sin sin cos cos cos sin sin()sin sin 0cos cos()cos cos 0L L L L L L L L L L L L L L θωθωθωθωθωθωθωθαωθωθωθωθαωθωθω⎧-⋅⋅+⋅⋅=⋅⋅⎪⋅⋅-⋅⋅=-⋅⋅⎪⎨-⋅⋅-⋅-⋅-⋅⋅-⋅⋅=⎪⎪⋅⋅+⋅-⋅+⋅⋅+⋅⋅=⎩化为矩阵形式为：2233222333'222255665'222255666111111111sin sin 00cos cos 00sin()sin 0sin sin cos()cos 0cos cos sin cos sin cos L L L L L L L L L L L L L L L L θθωθθωθαθθθωθαθθθωθθωθθ⎡⎤⎡⎤-⋅⋅⎢⎥⎢⎥⋅-⋅⎢⎥⎢⎥⋅⎢⎥⎢⎥-⋅--⋅-⋅-⋅⎢⎥⎢⎥⎢⎥⎢⎥⋅-+⋅⋅⋅⎣⎦⎣⎦⎡⋅⎢-⋅⎢=⋅⎢⋅⎢-⋅⎣⎤⎥⎥⎥⎥⎢⎥⎦3. 加速度方程矩阵对时间求一阶导数，可得加速度矩阵为：2233222333'222255665'2222556662233223322sin sin 00cos cos 00sin sin()0sin sin cos cos()0cos cos cos cos 00sin sin 00cos θθεθθεθθαθθεθθαθθεθθθθθ-⋅⋅⎡⎤⎡⎤⎢⎥⎢⎥⋅-⋅⎢⎥⎢⎥⋅=⎢⎥⎢⎥-⋅-⋅--⋅-⋅⎢⎥⎢⎥⋅+⋅-⋅⋅⎣⎦⎣⎦-⋅⋅-⋅⋅-⋅L L L L L L L L L L L L L L L L L 2112211231'2225566115'222225566116cos sin cos()0cos cos cos sin sin()0sin sin sin θωθωωθαθθθωθθαθθθω⋅⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⋅⎢⎥⎢⎥⎢⎥⋅+⋅⎢⎥⎢⎥⎢⎥-⋅--⋅-⋅⋅⎢⎥⎢⎥⎢⎥-⋅-⋅--⋅-⋅⋅⎢⎥⎣⎦⎣⎦⎣⎦L L L L L L L L L L L4. E 点运动分析1) 位移：⎩⎨⎧⋅-⋅+=⋅-⋅+=55665566sin sin cos cos θθθθL L y y L L x x G EG E2) 速度：⎪⎩⎪⎨⎧⋅⋅-⋅⋅=⋅⋅+⋅⋅-=555666555666cos cos sin sin ωθωθωθωθL L v L L v yx E E 3) 加速度：⎪⎩⎪⎨⎧⋅⋅-⋅⋅+⋅⋅+⋅⋅-=⋅⋅+⋅⋅+⋅⋅-⋅⋅-=5552555666266655525556662666cos sin cos sin sin cos sin cos εθωθεθωθεθωθεθωθL L L L a L L L L a yx E E三．计算程序框图开始输入L1,L2,L3,L4,L5,L6,L2’,xg,yg,ωI=0θ1=I*10°用矢量法求解角位移函数，并计算θ2，θ3，θ5，θ6，并计算Xe,Ye调用系数矩阵A子函数，计算A调用原动件位置参数矩阵B子程序，创建矩阵B调用求解角速度子程序，调用高斯消去法求解A*ω=B*ω1，得到ω2，ω3，ω5，ω6，再求解Vex，Vey调用系数矩阵DA，计算DA调用系数矩阵DB，计算DB调用求解角加速度子程序，计算B（K）= -DA*ω+DB*ω1,然后调用高斯消去法程序结A*a= B（K）求的a2，a3，a5，a6，再求出aex，aeyI=I+1I<3输出结果结束图2四．计算源程序#include<stdio.h>#include<stdlib.h>#include<math.h>#define PI 3.1415926#define N 4void Solutionangle(double [18],double ); /*矢量法求角位移*/void Solutionspeed(double [N][N],double [N],double [18],double ); /*角速度求解*/void Solutionacceleration(double [N][N],double [N][N],double [N],double [18]);/*角加速度求解*/void GaussianE(double [N][N],double [N],double [N]);/*高斯消去*/void FoundmatrixA(double [18],double [N][N]); //创建系数矩阵Avoid FoundmatrixB(double [18],double ,double [N]);//创建系数矩阵Bvoid FoundmatrixDA(double [18],double [N][N]);//创建矩阵DAvoid FoundmatrixDB(double [18],double ,double [N]);//创建矩阵DB//定义全局变量double l1=26.5,l2=105.6,l3=67.5,l4=87.5,l5=34.4,l6=25;double l2g=65.0,xg=153.5,yg=41.7,inang=PI/3,as1=1.0;//主函数int main(){int i,j;FILE *fp;double shuju[36][18];double psvalue[18],a[N][N],da[N][N],b[N],db[N],ang1;//建立文件，并制表头if((fp=fopen("file1.txt","w"))==NULL){printf("Cann't open this file.\n");exit(0);}fprintf(fp,"\n The Kinematic Parameters of Point 5\n");fprintf(fp," ang2 ang3 ang5 ang6");//计算数据并写入文件for(i=0;i<36;i++){ang1=i*PI/18;Solutionangle(psvalue,ang1);FoundmatrixB(psvalue,ang1,b);FoundmatrixA(psvalue,a);Solutionspeed(a,b,psvalue,ang1);FoundmatrixDA(psvalue,da);FoundmatrixDB(psvalue,ang1,db);Solutionacceleration(a,da,db,psvalue);//for(j=0;j<4;j++)//{shuju[i][j]=psvalue[j]*180/PI;}for(j=11;j<12;j++){shuju[i][j]=psvalue[j];}fprintf(fp,"\n");for(j=11;j<12 ;j++)fprintf(fp,"%12.3f",shuju[i][j]);}fclose(fp);if((fp=fopen("file2.txt","w"))==NULL){printf("Cann't open this file.\n");exit(0);}fprintf(fp,"\n The Kinematic Parameters of Point 5\n");fprintf(fp," ang2 ang3 ang5 ang6");fprintf(fp," as2 as3 as5 as6");fprintf(fp," aas2 aas3 aas5 aas6");fprintf(fp," xe ye vex vey aex aey\n");//计算数据并写入文件for(i=0;i<36;i++){ang1=i*PI/18;Solutionangle(psvalue,ang1);FoundmatrixB(psvalue,ang1,b);FoundmatrixA(psvalue,a);Solutionspeed(a,b,psvalue,ang1);FoundmatrixDA(psvalue,da);FoundmatrixDB(psvalue,ang1,db);Solutionacceleration(a,da,db,psvalue);for(j=0;j<4;j++){shuju[i][j]=psvalue[j]*180/PI;}for(j=4;j<18;j++){shuju[i][j]=psvalue[j];}fprintf(fp,"\n");for(j=0;j<18;j++)fprintf(fp,"%12.3f",shuju[i][j]);}fclose(fp);//输出数据for(i=0;i<36;i++){ang1=i*PI/18;printf("\n输出ang1=%d时的求解\n",i*10);printf("angle angspeed angacceleration\n");for(j=0;j<4;j++)printf("%lf\t",shuju[i][j]);printf("\n");for(j=4;j<8;j++)printf("%lf\t",shuju[i][j]);printf("\n");for(j=8;j<12;j++)printf("%lf\t",shuju[i][j]);printf("\n");for(j=12;j<16;j++)printf("%lf\t",shuju[i][j]);printf("\n");printf("E(x)\t\tE(y)\n");for(j=16;j<18;j++)printf("%lf\t",shuju[i][j]);printf("\n");}}/*矢量法求角位移*/void Solutionangle(double value[18],double ang1){int i;double xe,ye,A,B,C,phi,alpha,csn,ang5g,d2,d,ang2,ang3,ang5,ang6;A=2*l1*l3*sin(ang1);B=2*l3*(l1*cos(ang1)-l4);C=l2*l2-l1*l1-l3*l3-l4*l4+2*l1*l4*cos(ang1);ang3=2*atan((A+sqrt(A*A+B*B-C*C))/(B-C));if(ang3<0)//限定ang3大小{ang3=2*atan((A-sqrt(A*A+B*B-C*C))/(B-C));}ang2=asin((l3*sin(ang3)-l1*sin(ang1))/l2);xe=l4+l3*cos(ang3)+l2g*cos(ang2-inang);//求E点坐标ye=l3*sin(ang3)+l2g*sin(ang2-inang);phi=atan2((yg-ye),(xg-xe));d2=(yg-ye)*(yg-ye)+(xg-xe)*(xg-xe);d=sqrt(d2);csn=(l5*l5+d2-l6*l6)/(2.0*l5*d);alpha=atan2(sqrt(1.0-csn*csn),csn);ang5g=phi-alpha;ang5=ang5g-PI;ang6=atan2(ye+l5*sin(ang5g)-yg,xe+l5*cos(ang5g)-xg);value[0]=ang2;value[1]=ang3;value[2]=ang5;value[3]=ang6;value[12]=xe;value[13]=ye;//限定角度大小for(i=0;i<4;i++){while(value[i]>2*PI)value[i]-=2*PI;while(value[i]<0)value[i]+=2*PI;}}/*角速度求解*/void Solutionspeed(double a2[N][N],double b2[N],double value[18],double ang1){double ang2,ang3;ang2=value[0];ang3=value[1];double p2[N];GaussianE(a2,b2,p2);value[4]=p2[0];value[5]=p2[1];value[6]=p2[2];value[7]=p2[3];value[14]=-l3*value[5]*sin(ang3)-l2g*value[4]*sin(ang2-inang);value[15]=l3*value[5]*cos(ang3)+l2g*value[4]*cos(ang2-inang);}/*角加速度求解*/void Solutionacceleration(double a3[N][N],double da3[N][N],doubledb3[N],double value[18]){int i,j;double ang2,ang3;ang2=value[0];ang3=value[1];double bk[N]={0};double p3[N];for(i=0;i<N;i++){for(j=0;j<N;j++){bk[i]+=-da3[i][j]*value[4+j];}bk[i]+=db3[i]*as1;}GaussianE(a3,bk,p3);value[8]=p3[0];value[9]=p3[1];value[10]=p3[2];value[11]=p3[3];value[16]=-l3*value[9]*sin(ang3)-l3*value[5]*value[5]*cos(ang3)-l2g*value[8]*sin(a ng2-inang)-l2g*value[4]*value[4]*cos(ang2-inang);value[17]=l3*value[9]*cos(ang3)-l3*value[5]*value[5]*sin(ang3)+l2g*value[8]*cos(a ng2-inang)-l2g*value[4]*value[4]*sin(ang2-inang);}/*高斯消去法解矩阵方程*/void GaussianE(double a4[N][N],double b4[N],double p4[N]){int i,j,k;double a4g[N][N],b4g[N],t;for(i=0;i<N;i++)for(j=0;j<N;j++)a4g[i][j]=a4[i][j];for(i=0;i<N;i++)b4g[i]=b4[i];//使主对角线上的值尽可能大if(a4g[0][0]<a4g[1][0] && a4g[0][1]>a4g[1][1]){for(j=0;j<N;j++){t=a4g[0][j];a4g[0][j]=a4g[1][j];a4g[1][j]=t;}t=b4g[0];b4g[0]=b4g[1];b4g[1]=t;}if(a4g[2][2]<a4g[3][2] && a4g[2][3]>a4g[3][3]){for(j=0;j<N;j++){t=a4g[2][j];a4g[2][j]=a4g[3][j];a4g[3][j]=t;}t=b4g[2];b4g[2]=b4g[1];b4g[3]=t;}//初等行变换for(j=0;j<N;j++)for(i=0;i<N;i++){if(i!=j){for(k=0;k<N;k++)if(k!=j){a4g[i][k]-=a4g[i][j]/a4g[j][j]*a4g[j][k];}b4g[i]-=b4g[j]*a4g[i][j]/a4g[j][j];a4g[i][j]=0;}}for(i=0;i<N;i++)b4g[i]/=a4g[i][i];p4[0]=b4g[0];p4[1]=b4g[1];p4[2]=b4g[2];p4[3]=b4g[3];}//创建系数矩阵Avoid FoundmatrixA(double value5[18],double a5[N][N]){double ang2,ang3,ang5,ang6;ang2=value5[0];ang3=value5[1];ang5=value5[2];ang6=value5[3];a5[0][0]=-l2*sin(ang2);a5[0][1]=l3*sin(ang3);a5[1][0]=l2*cos(ang2);a5[1][1]=-l3*cos(ang3);a5[2][0]=-l2*sin(ang2)-l2g*sin(ang2-inang);a5[2][2]=-l5*sin(ang5);a5[2][3]=-l6*sin(ang6);a5[3][0]=l2*cos(ang2)+l2g*cos(ang2-inang);a5[3][2]=l5*cos(ang5);a5[3][3]=l6*cos(ang6);a5[0][2]=a5[0][3]=a5[1][2]=a5[1][3]=a5[2][1]=a5[3][1]=0;}//创建系数矩阵Bvoid FoundmatrixB(double value6[18],double ang1,double b6[N]){b6[0]=b6[2]=l1*sin(ang1)*as1;b6[1]=b6[3]=-l1*cos(ang1)*as1;}//创建矩阵DAvoid FoundmatrixDA(double value7[18],double da7[N][N]){double ang2,ang3,ang5,ang6,as2,as3,as5,as6;ang2=value7[0];ang3=value7[1];ang5=value7[2];ang6=value7[3];as2=value7[4];as3=value7[5];as5=value7[6];as6=value7[7];da7[0][0]=-l2*as2*cos(ang2);da7[0][1]=l3*as3*cos(ang3);da7[1][0]=-l2*as2*sin(ang2);da7[1][1]=l3*as3*sin(ang3);da7[2][0]=as2*(-l2*cos(ang2)-l2g*cos(ang2-inang));da7[2][2]=-as5*l5*cos(ang5);da7[2][3]=-as6*l6*cos(ang6);da7[3][0]=as2*(-l2*sin(ang2)-l2g*sin(ang2-inang));da7[3][2]=-as5*l5*sin(ang5);da7[3][3]=-as6*l6*sin(ang6);da7[0][2]=da7[0][3]=da7[1][2]=da7[1][3]=da7[2][1]=da7[3][1]=0;}//创建矩阵DBvoid FoundmatrixDB(double value8[18],double ang1,double db8[N]){db8[0]=db8[2]=l1*as1*cos(ang1);db8[1]=db8[3]=l1*as1*sin(ang1);}五．计算结果对于2-A组数据计算结果表2，表3，表4所示。
