例1-7-3判断系统是否为线性非时变系统
- 格式:ppt
- 大小:159.50 KB
- 文档页数:2




《信号与系统》第一次作业姓名:学号:1. 判断下列系统是否为线性系统,其中()y t 、[]y k 为系统的完全响应,(0)x 为系统初始状态,()f t 、[]f k 为系统输入激励。
(1)()(0)lg ()=y t x f t 解:在判断具有初始状态的系统是否线性时,应从三个方面来判断。
一是可分解性,即系统的输出响应可分解为零输入响应与零状态响应之和。
二是零输入线性,系统的零输入响应必须对所有的初始状态呈现线性特性。
三是零状态线性,系统的零状态响应必须对所有的输入信号呈现线性特性。
只有这三个条件都符合,该系统才为线性系统。
()(0)lg ()=y t x f t 不具有可分解性,所以系统是非线性系统。
(2)[](0)[][1]=+-y k x f k f k解:y[k]具有可分解性,零输入响应x(0)是线性的,但零状态响应f[k]f[k-1]是非线性的,所以系统是非线性系统。
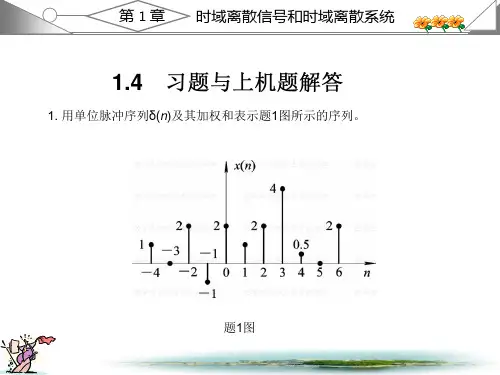
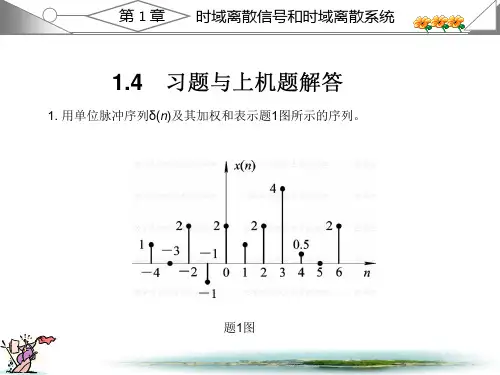
2. 判断下列系统是否为线性非时变系统,为什么?其中()f t 、[]f k 为输入信号,()y t 、[]y k 为零状态响应。
(1)()()()=y t g t f t解:在判断系统的时不变特性时,不涉及系统的初始状态,只考虑系统的零状态响应。
系统零状态响应,g(t)f(t)满足均匀性和叠加性,所以系统是线性系统。
因为T{f(t-t0)}=g(t).f(t-to)而 y(t-t0)=g(t-t0).f(t-t0) ≠T{f(t-t0)},故该系统为时变系统。
因此该系统为线性时变系统(2)220[][],(0,1,2,)+===∑k i y k kf i k 解:220[][],(0,1,2,)+===∑k i y k k f i k 为线性时变系统。
3. 已知信号()f t的波形如题1-3图所示,绘出下列信号的波形。
1t1f(t)-2-1-1题1-3图(1)(36)-+f t解:f(t) ——(波形数轴对称):f(-t)——【波形t轴方向,t值缩小至1/3,f(t)值不变】:f(-3t)——【波形往右横移6】:(36)-+f t最终画出波形图如下:(2)(1)3tf-+解:f(t) ——(波形数轴对称):f(-t)——【波形t轴方向,t值扩大3倍,f(t)值不变】:f(-⅓t)——【波形往右横移1】:(1)3tf-+最终画出波形图如下:4. 已知()(4)2(1)(1)2(1)tf t t t t t e u tδδδ-'=+-+++++,绘出()f t波形。


————第一章———— 时域离散信号与系统理论分析基础本章1.1节“学习要点”和1.2节“例题”部分的内容对应教材第一、二章内容。
为了便于归纳总结,我们将《数字信号处理(第二版)》教材中第一章和第二章的内容合并在一起叙述,这样使读者对时域离散线性时不变系统的描述与分析方法建立一个完整的概念,以便在分析和解决问题时,能全面考虑各种有效的途径,选择最好的解决方案。
1.1 学 习 要 点1.1.1 时域离散信号——序列时域离散信号(以下简称序列)是时域离散系统处理的对象,研究时域离散系统离不开序列。
例如,在时域离散线性时不变系统的时域描述中,系统的单位脉冲响应()n h 就是系统对单位脉冲响应()n δ的响应输出序列。
掌握()n δ的时域和频域特征,对分析讨论系统的时域特性描述函数()n h 和频域特性描述函数()ωj e H 和()z H 是必不可少的。
1. 序列的概念在数字信号处理中,一般用()n x 表示时域离散信号(序列)。
()n x 可看作对模拟信号()t x a 的采样,即()()nT x n x a =,也可以看作一组有序的数据集合。
要点 在数字信号处理中,序列()n x 是一个离散函数,n 为整数,如图1.1所示。
当≠n 整数时,()n x 无定义,但不能理解为零。
当()()nT x n x a =时,这一点容易理解。
当=n 整数时,()()nT x n x a =,为()t x a 在nT t =时刻的采样值,非整数T 时刻未采样,而并非为零。
在学习连续信号的采样与恢复时会看到,()n x 经过低通滤波器后,相邻的()T n nT 1~+之间的()t x a 的值就得到恢复。
例如,()n x 为一序列,取()()2n x n y =,n 为整数是不正确的,因为当=n 奇数时,()n y 无定义(无确切的值)。
2. 常用序列常用序列有六种:①单位脉冲序列()n δ,②矩形序列()n R N ,③指数序列()n u a n,④正弦序列()n ωcos 、()n ωsin ,⑤复指数序列nj eω,⑥周期序列。



§ 1.1 信号与系统信号(signal)消息(Message):在通信系统中,一般将语言、文字、图像或数据统称为消息。
信号(Signal):指消息的表现形式与传送载体。
信息(Information):一般指消息中赋予人们的新知识、新概念,定义方法复杂,将在后续课程中研究。
信号是消息的表现形式与传送载体,消息是信号的传送内容。
如电信号传送声音、图像、文字等。
电信号是应用最广泛的物理量,如电压、电流、电荷、磁通等。
系统(system)系统(system):由若干相互作用和相互依赖的事物组合而成的,具有稳定功能的整体。
如太阳系、通信系统【-----为传送消息而装设的全套技术设备(包括传输信道),其方框如下图所示:消息信号】、控制系统、经济系统、生态系统等。
系统可以看作是变换器、处理器。
电系统具有特殊的重要地位,某个电路的输入、输出是完成某种功能,如微分、积分、放大,也可以称系统。
在电子技术领域中,“系统”、“电路”、“网络”三个名词在一般情况下可以通用。
信号理论与系统理论信号理论信号分析:研究信号的基本性能,如信号的描述、性质等。
信号传输:通信的目的是为了实现消息的传输。
原始的光通信系统——古代利用烽火传送边疆警报;声音信号的传输——击鼓鸣金。
利用电信号传送消息。
1837年,莫尔斯(F.B.Morse)发明电报;1876年,贝尔(A.G.Bell)发明电话利用电磁波传送无线电信号。
1901年,马可尼(G.Marconi)成功地实现了横渡大西洋的无线电通信;全球定位系统GPS(Global Positioning System);个人通信具有美好的发展前景光纤通信带来了更加宽广的带宽。
信号的传输离不开信号的交换。
信号处理:对信号进行某种加工或变换。
其目的是:消除信号中的多余内容;滤除混杂的噪声和干扰;将信号变换成容易分析与识别的形式,便于估计和选择它的特征参量。
信号处理的应用已遍及许多科学技术领域。
合工大《数字信号处理》习题答案第2章习 题2.3 判断下面的序列是否是周期的,若是周期的,确定其周期。
(1))873cos()(ππ-=n A n x ,A 是常数; (2))81()(π-=n j e n x 。
2.3 (1)31420=ωπ,所以周期为14。
(2)πωπ1620=,是无理数,所以)(n x 是非周期的。
2.4 设系统分别用下面的差分方程描述,)(n x 与)(n y 分别表示系统输入和输出,判断系统是否是线性非时变的。
(1))()(0n n x n y -= (2))()(2n x n y = (3))sin()()(n n x n y ω= (4))()(n x en y =2.4 (1)由于)()]([0n n x n x T -=)()()]([0m n y n m n x m n x T -=--=-所以是时不变系统。
)()()()()]()([21020121n by n ay n n bx n n ax n bx n ax T +=-+-=+所以是线性系统。
(2))()()]([2m n y m n x m n x T -=-=-,所以是时不变系统。
)()()]()([)]()([2122121n by n ay n bx n ax n bx n ax T +≠+=+,所以是非线性系统。
(3))()sin()()]([m n y n m n x m n x T -≠-=-ω,所以不是时不变系统。
)()()sin()]()([)]()([212121n by n ay n n bx n ax n bx n ax T +=+=+ω,所以是线性系统。
(4))()()]()([21)()()]()([212121n by n ay e e e n bx n ax T n bx n ax n bx n ax +≠==++,所以是非线性系统。
)()]([)(m n y e m n x T m n x -==--,所以是时不变系统。