下载文档原格式
实验一信号与系统认知一、实验目的1、了解实验室的规章制度、强化安全教育、说明考核方法。
2、学习示波器、实验箱的使用、操作知识；3、学习常用连续周期信号的波形以及常用系统的作用。
二、实验仪器1、信号与系统实验箱（本次实验使用其自带的简易信号源，以及实验箱上的“信号通过系统”部分。
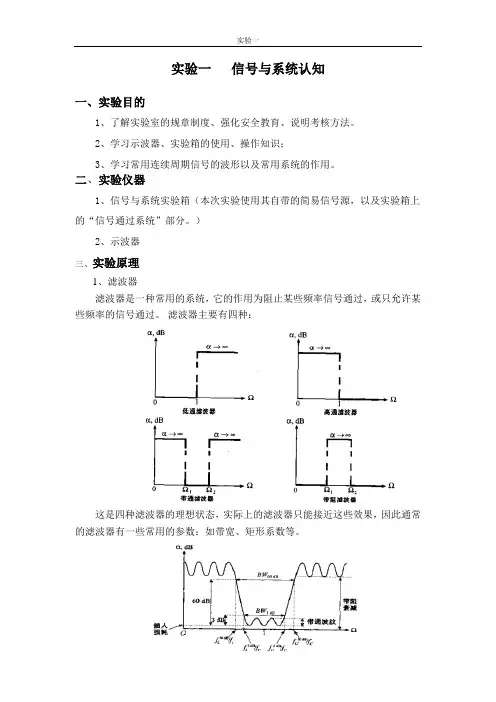
）2、示波器三、实验原理1、滤波器滤波器是一种常用的系统，它的作用为阻止某些频率信号通过，或只允许某些频率的信号通过。
滤波器主要有四种：这是四种滤波器的理想状态，实际上的滤波器只能接近这些效果，因此通常的滤波器有一些常用的参数：如带宽、矩形系数等。
通带范围：与滤波器最低衰减处比，衰减在3dB以下的频率范围。
2、线性系统线性系统是现实中广泛应用的一种系统，线性也是之后课程中默认为系统都具有的一种系统性质。
系统的线性表现在可加性与齐次性上。
齐次性：输入信号增加为原来的a倍时，输出信号也增加到原来的a倍。
四、预习要求1、复习安全操作的知识。
2、学习或复习示波器的使用方法。
3、复习典型周期信号的波形及其性质。
4、复习线性系统、滤波器的性质。
5、撰写预习报告。
五、实验内容及步骤1、讲授实验室的规章制度、强化安全教育、说明考核方法2、通过示波器，读出实验箱自带信号源各种信号的频率范围（1）测试信号源1的各种信号参数，并填入表1-1。
（2）测试信号源2的各种信号参数，并填入表1-2。
3、测量滤波器根据相应测量方法，用双踪示波器测出实验箱自带的滤波器在各频率点的输入输出幅度（先把双踪示波器两个接口都接到所测系统的输入端，调节到都可以读出输入幅度值，并把两侧幅度档位调为一致，记录下这个幅度值；之后，将示波器的一侧改接入所测系统的输出端，再调节用于输入的信号源，将信号频率其调至表1-3中标示的值，并使输入信号幅度保持原幅度值不变。
观察输出波形幅度的变化，并与原来的幅度作比较，记录变化后的幅度值。
），并将相应数据计入表1-3中。
4、测量线性系统（1）齐次性的验证自选一个输入信号，观察输出信号的波形并记录输入输出信号的参数，将输入信号的幅度增强为原信号的一定倍数后，再对输入输出输出参数进行记录，对比变化前后的输出。
信号与系统的数学基础
信号与系统是一门涉及到信号处理和系统分析的学科，其数学基础主要包括以下几个方面：
1. 微积分：微积分是信号与系统中最基本的数学工具，用于描述信号的变化率和系统的响应。
2. 线性代数：线性代数用于表示信号和系统的线性组合、向量和矩阵等概念，以及求解线性方程组。
3. 概率论与随机过程：概率论和随机过程用于描述信号和系统中的随机现象，如噪声和干扰。
4. 复变函数：复变函数用于描述信号在复数域中的表示和运算，以及系统的复数域分析。
5. 离散数学：离散数学用于描述离散时间信号和系统，如数字信号处理和数字通信系统。
6. 常微分方程和偏微分方程：常微分方程和偏微分方程用于描述连续时间信号和系统的动态行为，如滤波器设计和信号传输。
以上是信号与系统的数学基础的主要方面，这些数学工具在信号与系统的理论分析和实际应用中都起着重要的作用。
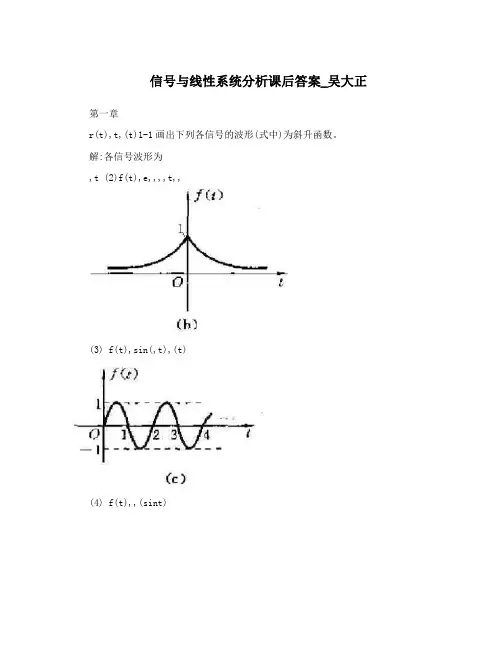
信号与线性系统分析课后答案_吴大正第一章r(t),t,(t)1-1画出下列各信号的波形(式中)为斜升函数。
解:各信号波形为,t (2)f(t),e,,,,t,,(3) f(t),sin(,t),(t)(4) f(t),,(sint)(5) f(t),r(sint)k(7) f(t),2,(k)k(10) f(k),[1，(,1)],(k)r(t),t,(t)1-2 画出下列各信号的波形[为斜升函数]。
f(t),r(t),2r(t,1)，r(t,2)f(t),2,(t，1),3,(t,1)，,(t,2) (1) (2) f(k),k[,(k),,(k,5)]f(t),r(2t),(2,t) (5) (8),kkf(k),sin()[,(k),,(k,7)]f(k),2[,(3,k),,(,k)](11) (12) 6解:各信号波形为f(t),2,(t，1),3,(t,1)，,(t,2) (1)f(t),r(t),2r(t,1)，r(t,2) (2)f(t),r(2t),(2,t) (5)f(k),k[,(k),,(k,5)] (8),kf(k),sin()[,(k),,(k,7)](11) 6kf(k),2[,(3,k),,(,k)](12)1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是，确定其周期。
3,,,,f(t),3cost，2sin(,t)f(k),cos(k，)，cos(k，) (2) (5) 524436 解:f(t)1-6 已知信号的波形如图1-5所示，画出下列各函数的波形。
f(0.5t,2)f(1,2t)f(t,1),(t)f(t,1),(t,1) (1) (2) (5) (6) tdf(t)f(x)dx (7) (8) ,,,dt解:各信号波形为f(t,1),(t) (1)f(t,1),(t,1) (2)f(1,2t) (5) f(0.5t,2) (6)df(t)(7) dttf(x)dx (8) ,,,f(k)1-7 已知序列的图形如图1-7所示，画出下列各序列的图形。
线性系统理论和设计是控制工程中的重要内容，涉及到对线性系统的建模、分析和控制设计。
以下是关于线性系统理论和设计的基本内容：
1. 线性系统模型
-线性系统描述：线性系统是指具有线性性质的动态系统，其输出与输入之间满足线性关系。
-线性系统模型：通常用微分方程、差分方程或状态空间方程描述线性系统的动态特性。
2. 线性系统分析
-系统稳定性分析：通过研究系统的零点、极点等性质来判断系统的稳定性。
-频域分析：通过频率响应、波特图等方法分析系统在频域下的性能。
-时域分析：通过阶跃响应、脉冲响应等方法研究系统在时域下的响应特性。
3. 线性系统设计
-控制器设计：设计合适的控制器来实现系统的性能要求，常见的控制器包括比例积分微分（PID）控制器、根轨迹设计等。
-系统鲁棒性设计：设计具有鲁棒性的控制器，能够抵抗参数变化和外部干扰的影响。
-最优控制设计：利用最优控制理论设计最优的控制器，使系统性能
达到最佳。
4. 线性系统应用
-自动控制系统：将线性系统理论和设计方法应用于自动控制系统，实现对各种工程系统的自动控制和调节。
-信号处理系统：利用线性系统理论设计数字滤波器、信号处理算法等，对信号进行处理和提取。
-机电系统：应用线性系统理论设计机电系统的控制器，实现机电系统的精密控制和运动规划。
线性系统理论和设计在控制工程领域具有广泛的应用，能够帮助工程师分析和设计各种复杂系统的控制策略，提高系统的性能和稳定性。
一、填空题（每空1分，共30分）1、无线电通信中，信号是以电磁波形式发射出去的。
它的调制方式有调幅、调频、调相。
2、针对不同的调制方式有三种解调方式，分别是检波、鉴频、和鉴相。
3、在单调谐放大器中，矩形系数越接近于1、其选择性越好；在单调谐的多级放大器中，级数越多，通频带越窄、（宽或窄），其矩形系数越（大或小）小。
4、调幅波的表达式为：uAM（t）= 20（1 +0.2COS100πt）COS107πt（V）；调幅波的振幅最大值为24V，调幅度Ma为20℅，带宽fBW为100Hz，载波fc为5*106Hz。
5、在无线电技术中，一个信号的表示方法有三种，分别是数学表达式、波形、频谱。
6、调频电路有直接调频、间接调频两种方式。
7、检波有同步、和非同步检波两种形式。
8、反馈式正弦波振荡器按照选频网络的不同，可分为LC、RC、石英晶振等三种。
9、变频器可由混频器、和带通滤波器两部分组成。
10、列出三个常见的频谱搬移电路调幅、检波、变频。
11、用模拟乘法器非线性器件实现调幅最为理想。
一、填空题（每空1分，共30分）1、接收机分为直接放大式、和超外差式两种。
2、扩展放大器通频带的方法有组合电路法、负反馈法和集成电路法三种。
3、在集成中频放大器中，常用的集中滤波器主要有：LC带通滤波器、陶瓷、石英晶体、声表面波滤波器等四种。
4、丙类谐振功放有欠压、临界和过压三种工作状态，其性能可用负载特性、调制特性和放大特性来描述。
5、普通调幅波的数学表达式UAMt=Ucm（1+Ma cosΩt）cosωct，为了实现不失真调幅，Ma一般≤1。
6、实现AGC的方法主要有改变发射级电流IE和改变放大器的负载两种。
7、根据频谱变换的不同特点，频率变换电路分为频谱搬移电路和频谱的非线性变换电路。
8、要产生较高频率信号应采用、LC振荡器，要产生较低频率信号应采用RC振荡器，要产生频率稳定度高的信号应采用石英晶体振荡器。
9、三点式振荡器有电容和电感三点式电路。
信号与系统试题附答案信科0801《信号与系统》复习参考练习题一、单项选择题：17、如图所示：f （t ）为原始信号，f 1(t)为变换信号，则f 1(t)的表达式是（ ）A 、f(－t+1)B 、f(t+1)C 、f(－2t+1)D 、f(－t/2+1)18、若系统的冲激响应为h(t),输入信号为f(t),系统的零状态响应是（ ）19。
信号)2(4sin 3)2(4cos 2)(++-=t t t f ππ与冲激函数)2(-t δ之积为（ ）A 、2B 、2)2(-t δC 、3)2(-t δD 、5)2(-t δ，则该系统是（）＞－系统的系统函数．已知2]Re[,651)(LTI 202s s s s s H +++=A 、因果不稳定系统B 、非因果稳定系统C 、因果稳定系统D 、非因果不稳定系统21、线性时不变系统的冲激响应曲线如图所示，该系统微分方程的特征根是（ ）A 、常数B 、 实数C 、复数 D 、实数+复数22、线性时不变系统零状态响应曲线如图所示，则系统的输入应当是（ ）A 、阶跃信号B 、正弦信号C 、冲激信号 D 、斜升信号23. 积分⎰∞∞-dt t t f )()(δ的结果为( )A )0(fB )(t f C.)()(t t f δD.)()0(t f δ24. 卷积)()()(t t f t δδ**的结果为( )A.)(t δB.)2(t δC.)(t f D.)2(t f25. 零输入响应是( )A.全部自由响应B.部分自由响应C.部分零状态响应D.全响应与强迫响应之差 2A 、1-eB 、3eC 、3-e D 、1 27.信号〔ε(t)－ε(t －2)〕的拉氏变换的收敛域为( )A.Re[s]>0B.Re[s]>2C.全S 平面D.不存在28．已知连续系统二阶微分方程的零输入响应)(t yzi 的形式为tt BeAe2--+，则其2个特征根为( )A。
