数学建模示例--价格竞争问题

2019数学建模薄利多销题目一、问题背景在当今经济全球化的背景下，企业需要在不断增长的竞争中保持竞争力。

产品的薄利多销是企业常用的一种策略，也是一个具有挑战性的问题。

在这个背景下，2019年的数学建模比赛就提出了薄利多销的相关题目，希望参赛选手们能够以数学建模的方法来解决这一难题。

二、问题描述1. 场景一：零售业假设有一个零售商，他在一段时间内售卖某种商品。

该商品的成本是已知的，而售价可以自行设定。

零售商希望通过调整售价来获得最大的利润。

然而，售价的高低又必须考虑到市场的竞争情况。

如何确定最佳的售价，使得利润最大化，是一个需要解决的数学问题。

2. 场景二：制造业一家制造企业生产某种产品，该产品的售价和成本也是已知的。

企业希望通过生产技术和管理手段来降低成本，以获得更大的利润。

如何在不影响产品质量的情况下，最大程度地降低成本，也是一个需要解决的数学问题。

三、问题分析1. 需求分析对于零售业而言，最大利润的获得需要考虑市场需求和竞争情况。

如果售价过高，可能导致顾客流失；如果售价过低，可能导致利润过低。

需要通过数学模型来分析市场需求和竞争状况，以确定最佳的售价。

对于制造业而言，最大利润的获得则需要考虑生产成本和产品质量。

通过数学模型来分析生产过程中的各个环节，优化生产方案，降低成本，以获得更大的利润。

2. 方法分析在解决这一问题时，可以采用数学建模中常用的优化方法，如线性规划、动态规划等。

另外，也可以结合市场调研数据和实际案例，通过数据分析的方法来验证数学模型的有效性。

四、解决方案1. 对于零售业可以建立一个利润最大化的数学模型，包括市场需求函数、竞争函数、成本函数和利润函数。

然后通过求解最优售价来获得最大利润。

2. 对于制造业可以建立一个成本最小化的数学模型，包括生产过程中的各个环节的成本函数和质量函数。

然后通过优化生产方案，降低成本来达到成本最小化的目标。

五、实施方案1. 数据采集需要对市场需求、竞争情况、生产成本等方面进行数据采集，以建立数学模型所需的参数。

利用数学模型解析市场问题市场是一个充满竞争和变化的环境，因此对市场问题进行数学建模和分析可以帮助我们更好地理解和解决这些问题。

本文将介绍几个常见的市场问题，并展示使用数学模型解析这些问题的方法。

首先，我们来看看市场供需模型。

在市场中，供应商和需求者的行为将决定市场的价格和数量。

供给是指将商品提供给市场的数量，而需求是指市场上消费者愿意购买的数量。

供需的平衡将决定市场的价格和数量。

为了建立供需模型，我们需要确定供给曲线和需求曲线。

供给曲线表示供应商愿意在不同价格下提供的数量，而需求曲线表示消费者愿意在不同价格下购买的数量。

通过将供给曲线和需求曲线相交，我们可以确定市场的均衡价格和数量。

接下来，我们考虑市场竞争问题。

在具有多个供应商和需求者的市场中，供应商之间和消费者之间将展开竞争。

这可能会导致价格的变动和市场份额的变化。

为了解析这个问题，我们可以使用博弈论模型。

博弈论是研究决策制定者之间相互作用的数学工具。

在市场中，供应商可以选择价格和数量策略，而消费者可以选择购买的数量。

通过分析其决策和反应，我们可以确定最优策略和均衡结果。

除了供需模型和博弈论模型，还有其他一些数学模型可以用于解析市场问题。

例如，回归分析可以帮助我们确定市场变量之间的关系。

时间序列分析可以用来预测市场的未来趋势。

最优化模型可以帮助我们确定最优的资源分配策略。

在解析市场问题时，我们需要注意模型的假设和局限性。

市场是一个复杂的系统，存在各种因素的相互影响。

因此，我们的模型只能提供对市场行为的简化描述，并不能完全反映真实情况。

此外，模型的结果也需要根据实际情况进行解释和调整。

总结起来，数学模型是解析市场问题的有力工具。

通过建立供需模型、博弈论模型和其他数学模型，我们可以更好地理解市场行为，并从中获取有用的信息和见解。

然而，我们也需要意识到模型的局限性，并将其结果与实际情况相结合，以获得更准确和可靠的分析。

伯特兰德（Bertrand ）价格竞争模型伯特兰德模型是由法国经济学家约瑟夫·伯特兰德（Joseph Bertrand ）于1883年提出的一个竞争模型。

它是分析寡头垄断市场上企业价格竞争的模型，这与古诺竞争模型是不同的。

古诺模型是把产量作为企业决策的变量，是一种产量竞争模型。

实际上，在企业的实际竞争过程中，定价是企业决策更基本的战略，每个企业所面临的消费者需求的大小往往取决于其定价。

特别是当市场上企业的数量较少时，企业在定价策略上的差异对企业产品需求的影响更为明显。

因此，伯特兰德模型对于研究寡头垄断企业的价格竞争行为的特征及其影响具有重要作用。

一、生产同质产品的伯特兰德竞争模型假定市场上只有两家企业：企业1和企业2，双方同时定价，它们生产的产品完全相同（即同质），寡头企业的成本函数也完全相同：生产的边际成本等于单位成本c ，且假设不存在固定成本。

市场需求函数()P D 是线性函数，相互之间没有任何正式的或非正式的串谋行为。

由于两个寡头垄断企业生产的产品同质，因而具有完全的替代性，所以两个企业中定价低者将获得所有需求，而定价高者将失去整个市场；如果两个企业定价相同，则他们将平分市场。

即若有企业1、企业2两企业，若企业1的定价1P 低于企业2的定价2P ，则企业1获得的需求)(1P D 将是整个市场的需求，而企业2的市场需求则为零；若双方定价相同，1P =2P =P ，则双方将平分市场，都将获得相当于整个市场需求量的一半，即21()P D 。

在上述情况下，两个企业中每一个企业的最优定价战略取决于其对另一家企业定价的推测。

（1）假设企业1预计企业2的定价将高于垄断价格，那么企业1的最优战略是按照垄断水平定价，此时它将获得所有的需求和垄断利润（即可能的最大利润）。

（2）假如企业1预计企业2的定价低于垄断水平，但高于边际成本，那么企业1的最优战略是定价略低于企业2，价格制定得偏高会导致零需求和零利润，而价格制定得略低将使企业1获得所有的需求，但利润要少一些。

装订线摘要自２0世纪末走出低谷以来，我国房地产业得以迅猛地发展,其势头受到世人的瞩目，它作为国民经济的支柱产业不仅对国家宏观经济运行产生巨大的影响,而且它与广大百姓的自身利益休戚相关。

住房问题关系国计民生,既是经济问题，更是影响社会稳定的重要民生问题。

２008 年受国际金融危机的影响,部分购房需求受到抑制，200９年在国家税收、土地等调控政策作用下，一度受到抑制的需求得到释放，适度宽松的货币政策使信贷规模加大,为房地产开发和商品房购买提供了比较充裕的资金,房地产市场供求大增，带动了整体回升。

但有的城市房价过高，上涨过快，加大了居民通过市场解决住房问题的难度，另一方面，部分投机者也通过各种融资渠道买入房屋囤积,期望获得高额利润,也是导致房价居高不下的原因之一。

因此,如何有效遏制房价过快上涨,遏制房地产投机,是一个备受关注的社会问题。

为此,国家在2010年 4 月17 日出台了《关于坚决遏制部分城市房价过快上涨的通知》(俗称为“新国十条”）的调控政策。

论文依据中国国情,统计分析建筑成本、居民收入等与房价密切相关的数据,选取我国具有代表性的几类城市对房价的合理性及房价的未来走势等问题进行定量分析;根据分析结果，进一步探讨使得房价合理的具体措施，以及可能对经济发展产生的影响，并进行定量分析。

关键词: 房价ﻩ地价指数人均收入ﻩ地价ﻩ数学模型目ﻩ录一、问题提出：............................................................................. 错误!未定义书签。

二、问题分析：............................................................................. 错误!未定义书签。

三、基本假设:ﻩ错误!未定义书签。

四、建立模型：ﻩ错误!未定义书签。

一、假设参数：...................................................................... 错误!未定义书签。

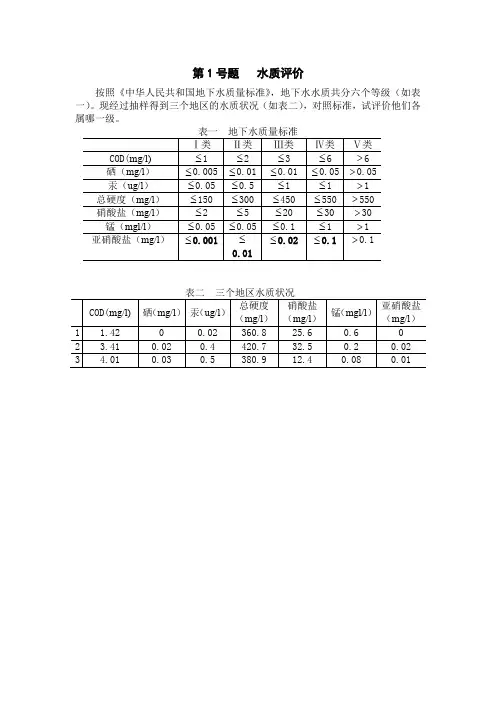
第1号题水质评价按照《中华人民共和国地下水质量标准》，地下水水质共分六个等级（如表一）。

现经过抽样得到三个地区的水质状况（如表二），对照标准，试评价他们各属哪一级。

第2号题工资比较为研究工资水平与工作年限和性别之间的关系，在某行业中随机抽取10名职工，所得数据如表一所示，试通过回归方程分析月工资收入与性别和工作年限有何关系。

表一 10名职工工资水平、工作年限和性别数据第3号题农产品定价某国政府要为其牛奶、奶油和奶酪等奶制品定价。

所有这些产品都直接或间接的来自国家的原奶生产。

原奶首先要分离成脂肪和奶粉两中组合，去掉生产出口产品和农场消费的产品的部分后，余下的共有60万吨脂肪和70万吨奶粉，可用于生产牛奶、奶油和两种奶酪，供国内全年消费。

各种产品的百分比组成见下表：产品\成分脂肪奶粉水牛奶4987奶油80218奶酪1353035奶酪2254035往年的国内消费和价格如下表：产品牛奶奶油奶酪1奶酪2消费量（千吨）482032021070价格（元/吨）2977201050815价格的变化会影响消费需求。

为表现这方面的规律，定义需求的价格伸缩性E：E=需求降低百分数/价格提高百分数各种产品的E值，可以据往年的价格而后需求变化情况的统计数据，用数理统计方法求出。

另外，两种奶酪的需求，随它们价格的相对变化，在某种程度上可以相互替代。

表现这一规律要用需求关于价格的交叉伸缩性EAB定义作：EAB=A需求提高百分数/B价格提高百分数奶酪1到奶酪2的E12值和奶酪2到奶酪1的交叉伸缩性E21值,同样可以凭数据用统计方法求出已经求出牛奶、奶油、奶酪1、奶酪2的E值依次为0.4，2.7，1.1和0.4以及E12=0.1, E21=0.4.试求出4种产品的价格，试所导致的需求使销售总收入为最大。

然而，政策不允许某种价格指标上升，这使得新的价格必须使消费的总费用较上一年度不增加。

因此，对问题的一个特别重要的附加要求，是对这一政策限制的经济代价，给出数量表示。

关于市场竞争问题的数学模型某个产品市场，由A公司垄断，现在B公司已具备了开发能力，其可变成本20万元，比A公司高20%，并且已经发布消息，问：以B公司的条件是否能参与市场竞争？一、模型的建立与求解1.采购与存储。

只考虑仓库之库存产品的简单情形：符号说明：k：表示生产线运行时商品的生产速率。

r:表示商品的销售速率(r<k)。

Q:表示商品的庫存量。

b:一个生产周期内的生产成本。

N：单位时间的总费用。

S:单位时间内单位产品的存放费用。

仓库的库存以下列方式变化;开始时边生产边销售，库存量以速率k-r增加，到时刻t只销售不生产，Q以速率r减少到时刻T，Q减少到零。

如此为一个周期。

如图所示：问题即为：确定周期T，使单位时间总费用最小。

由以上分析可知：单位时间成本为:b/T单位时间库存费为：由一个周期内生产的商品等与销售的商品得:kt=rt则单位时间总费用为:即表明：最优周期与生产成本的平方根成正比，与存储费用的平方根成反比。

单位时间总费用与生产成本和存储费用的平方根成正比。

2.仓库处存放产品外还存放原料:设一个周期生产所需原料一次备足，即t=0时，仓库要存放能生产kt件商品的原料。

设为单位时间内单位原料的存储费用。

由于生产速率为常数，则原料线性递减，t时刻时原料用完，生产停止。

如图:由图，单位时间原料存放费为，此时，单位时间总费用为：显然，该结果与第一步的结果形式相同，只是存储费部分加上了原料的存储费用，使得总费用增加。

同理，也可得出与第一步相同的结论：生产成本与产品和原料存储费用的比值在一定条件、一定范围内越大越好。

3.采购原料的最佳时机及一次采购数量:符号说明:a0:一次采购的手续费。

b0:单位数量的原料价格。

T0:原料的采购周期。

在这一步中，假设原料不许缺货，一旦短缺立即订货，且瞬时到货。

与第二步的分析同理，共采购能生产kt｀件商品的原料，生产过程中原料数量呈线性递减，在t`时刻原料用完，生产停止。