四年级奥数 第8讲 有趣的数阵图

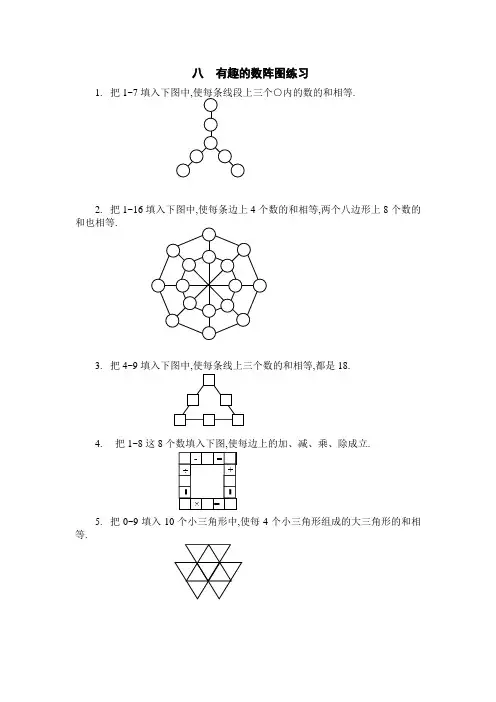
八 有趣的数阵图练习
1. 把1~7
.
2. 把
1~16填入下图中,使每条边上4个数的和相等,两个八边形上8个数的和也相等.
3. 把4~9填入下图中,使每条线上三个数的和相等,都是18.
4. 把1~8这8个数填入下图,使每边上的加、减、乘、除成立.
5. 把0~9
填入10个小三角形中,使每4个小三角形组成的大三角形的和相等.
6. 把1~11填入图中,使每条线上三个数的和相等.
7. 把1~8,填入图中,使每条线及正方形四个顶点上的数的和相等.
8. 把1~9,填入下图中,使每条线段三个数和及四个顶点的和也相等.
9. 把17,23,25,31,46,53,58,66,72,88,94,100十二个数填入下图,使任意三个相邻的数相加的和除以7的余数相等.。

使每个大圆圈上4个数的和都是16，你能办到吗？
1
5
2
4
6
3
猴博士送你一句数学家名言：
有趣的数阵图
四年级上学期 《数学探究 我快乐》第51页～54页
让猴博士告诉你
将一些数按照一定的规律排列而成的图 形，通常叫做数阵图。
例1 在下面的三角形数阵图的 里，填入 适当的数，使三边上3个 里的数的和是12。
5
1
3
6
2
4
猴博士考考你
在正方形数阵图中的 里填入适当的数，使 每条线上的3个数的和等于21。
4
11
6975 Nhomakorabea8
3 10
例2 在下面图中的 里，填上适当的数，使 每条线上3个 里的数的和等于13。
8
1
4
3 6
2 7
猴博士考考你
把10到20这11个数填在图中的 条线段上的3个数的和等于45。
里，使每
20
16 14
10
19
11
15
13
12
17
18
例3、把1、2、3、4、5这5个自然数填入到图 中的 里，使每条线段上的3个数的和相等。
1
猴博士考考你
把3到7这5个数分别填入到“T”和“十”字形 的方格内，使横、竖两行的3个数的和相等。
3 3
和猴博士一起玩个数学游戏好吗？
第一关 把1、2、3、4、5、6、7这7个数字填入图中
的 里，使每条线上的 里的3个数的和相等。
6
1
7 32
4
5
第二关 将1、2、3、4、5、6填入到下面的小圆圈里，

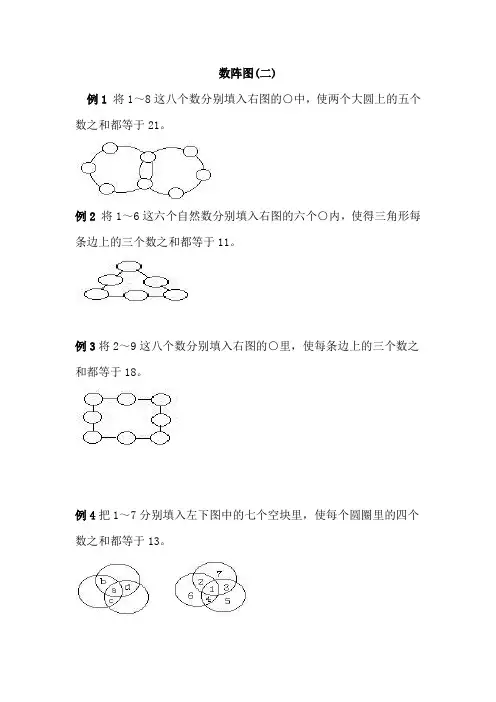
数阵图(二)
例1将1～8这八个数分别填入右图的○中，使两个大圆上的五个数之和都等于21。

例2将1～6这六个自然数分别填入右图的六个○内，使得三角形每条边上的三个数之和都等于11。

例3将2～9这八个数分别填入右图的○里，使每条边上的三个数之和都等于18。

例4把1～7分别填入左下图中的七个空块里，使每个圆圈里的四个数之和都等于13。

1.把1～8填入下页左上图的八个○里，使每个圆圈上的五个数之和都等于20。

2.把1～6这六个数填入右上图的○里，使每个圆圈上的四个数之和都相等。

3.将1～8填入左下图的八个○中，使得每条边上的三个数之和都等于15。

4.将1～8填入右上图的八个○中，使得每条直线上的四个数之和与每个圆周上的四个数之和都相等。

5.将1～7填入右图的七个○，使得每条直线上的各数之和都相等。

6.把1，3，5，7，9，11，13分别填入左图中的七个空块中，使得每个圆内的四个数之和都等于34。

1
猴博士考考你
把3到7这5个数分别填入到“T”和“十” 字形的方格内，使横、竖两行的3个数的和 相等。
3 3
和猴博士一起玩个数学游戏好吗？
第一关 把1、2、3、4、5、6、7这7个数字填入图中 的 里，使每条线上的 里的3个数的和相等。
6 1 3 7 2
4
5
第二关 将1、2、3、4、5、6填入到下面的小圆圈里， 使每个大圆圈上4个数的和都是16，你能办到吗？
有趣的数阵图
四年级上学期 《数学探究 我快乐》第51页～54页
金坛市金城镇中心小学
丁国新
让猴博士告诉你
将一些数按照一定的规律排列而成的图 形，通常叫做数阵图。
例1 在下面的三角形数阵图的 里， 填入适当的数，使三边上3个 里的数的和 是12。
5
1
3 2
4
6
猴博士考考你
在正方形数阵图中的 里填入适当的 数，使每条线上的3个数的和等于21。
1
5
2
4
6
3
猴博士送你一句数学家名言：
数学好玩！
陈省身
谢谢各位！
； /kxiantu/ k线理论
ath18cwb
蹭过来，谁知 吩咐的是：“我身子如此，不得向诸长辈和姐妹们问安，你且替我去请安、问好、道声惭愧。”请安问好，是露脸的事啊， 光明正大可去菊花会上了，还不用偷溜的！乐韵喜出望外，当即答应下来——话说回来了，表 一向身子太弱，几乎所有的亲族活动都不参 加，也不屑得跟人面子上交代交代，今儿怎么开窍了？乐韵有些疑惑。“对了，替我给诸长辈与姐妹们带些礼物去罢！”宝音道，“你看 带些什么去好？”带点见面礼，哪怕是一朵花一根草呢，接受方出于情面，就要对乐韵有所赏赐了！带个见面礼是好的！乐韵果然拼命动 脑袋的想，临急临忙拿些什么去呢？自家人原不用太贵重，表 屋里也没什么好东西，每个人都送过来太难办……对了！重阳菊花会，就送 花儿罢！乐韵嘻嘻笑道：“ 屋后那两株芙蓉开得倒好，不如乐韵剪一篮子，送去给奶奶姑娘们添妆如何？”芙蓉？宝音微微一怔，想起来， 应该说的是表 屋后木芙蓉树，算起来，现在倒正在着花时候，攒上一篮子没问题，统总拎过去，谁爱拿就拿，做个整团儿人情，可不比给 每人准备礼物来得便当。乐韵在这方面，果然有急智。她点头道：“便是这样罢！”洛月注目宝音，分明想问，那两株木芙蓉，是 心爱之 物，平常都舍不得让人接近的，今儿怎么舍得让人剪了去？真要是韩玉笙在，听了乐韵建议，准气得咳血，不准动花儿分毫，宝音却想花 开无非要谢的，竟不如往合适的地方去，因此轻轻易易便准了。乐韵只怕宝音反悔，忙着道：“那姑娘快休息要紧！乐韵自会照料得。” 兴冲冲往门外去，宝音冷不丁又丢出来一句：“午前必要回还！”乐韵想想，她的午饭按例还在表 屋里开，菊花会那边有头有脸的人都在， 要蹭也不太好蹭，可不要回来吃饭么？这条却使得的，便应了，去掇个竹匾，寻个花剪，挎个三腿小圆凳往后头去。且喜两棵树都生得不 高，踩上凳子，就够到了下头的枝干，咔嚓咔嚓剪起来。这树一株大红、一株粉白。洛月剪完了一色，又去剪另一色，猛抬头看见邱妈妈 拢着手、虎着脸瞪着自己。乐韵一时头皮有些发麻，叫了声“邱妈妈”，辩解道：“这次可是姑娘叫我剪的，您也看见了！”邱妈妈哼了 一声，走开。临走丢下一句话：“仔细摔断你的腿！”乐韵呆了会儿，恨恨举手，“咔叭”又剪下去。这一篮子鲜洁丰丽芙蓉花朵挎去菊 花宴上，众人们反应多半是：“哟，今儿笙妹妹怎么想着我们？”各各拣了几朵，就席面上多多少少也给了乐韵一些儿赏，乐韵勾留至近 午，一向相熟的丫头筱筱过来问她：“你留在这儿吃么？听说今儿中午有九品羹，还有芋大嫂拿手的鲜虾蛋卷，连我们下头人都有份！” 乐韵还未回答，筱筱又“哦”了一声：“不过我是跟着我们四姑娘，才有

四年级奥数讲义:有趣的数阵图（一）大家都知道了历史悠久的三阶幻方.再推广一些,结合某些几何图形,把一些数字填入图形的某种位置上,并使数字满足一定的约束条件,这类问题,习惯上称为“数阵图”.幻方是特殊的数阵图,幻方发展较快,因为它后来与试验方案设计及一些高深数学分支有关,成为数阵图中最重要课题.本讲主要介绍一般数阵图及解此类题的推理思考方法,由于它既有数字之间运算,又要结合图形,对开发学生综合思考和形象思维很有益.先看例题.例 1 下面图形包括六个加法算式,要在圆圈里填上不同的自然数,使六个算式都成立,那么最右边圆圈中的数最少是几？分析为便于说理,各圆圈内欲填的数依次用字母A、B、C、D、E、F、G、H、I代替（上右图）.经观察,I=A+B+C+D.题目要I尽可能小,最极端的想法,希望A、B、C、D只占用1、2、3、4.但这会产生矛盾.因为1总要和2、3、4中的某两个实施加法,但1＋2给予G、H、E、F中某值为3与A、B、C、D中已有的3冲突；同样1+3给于G、H、E、F中某值为4又与A、B、C、D中已有的4冲突；所以A、B、C、D不能是1、2、3、4.那么退而求之,不妨先设A=1.如先考虑B,B尽可能小,最好,B=2,从而决定了E=3,C≠3,D≠3.这样一来,C,D只能取4和5.但如C=4导致G=5和D=5冲突,而C=5,D=4,又导致G=A+C=6和H=B+D=2+4=6冲突.在碰了钉子后,回看在A=1设定后,不应随随便便先填B的值.从结构上看,因为B,C地位对称,不妨先考虑D.D尽可能小,最好设D=2,B、C至少取3、5,若如此,由B+D或C+D产生的5会与B、C中已有的5矛盾.所以,B、C可能取3、6.从而形成了:A=1、D=2、B、C取3、6（B,C地位对称）.这样一来其他字母所代表的值就立即推出,不妨设B=3,C=6,A+B=E=4,C+D=6+2=8=F；A+C=1+6=7=G,B+D=3+2=5=H,恰好满足E+F=4+8=12=I；G+H=7+5=12=I；综上所述:A=1,D=2,B=3,C=6决定了其他值,且决定了I=12.是一个较小的I的值,自然要问I 值还可能比12小吗？分析I的值有三种不同的获得方式:I=A+B+C+D=E+F=G+H.3I=A+B+C+D+E+F+G+H,而8个字母最少是代表1、2、…、7、8的情况.3I≥（1+2+…+7+8）=36,I≥12.现已推出了使I=12的一种填法,所以是最佳方案了.例2 如右图,五圆相连,每个位置的数字都是按一定规律填写的,请找出规律,并求出x所代表的数.分析经观察,图中所填数的规律为两个圆相交部分的数等于与它相邻两部分里的数的和的一半.比如:（26+18）÷2=22.（30+26）÷2=28.（24+30）÷2=27.解: x+18=17×2x=16.经检验,16和24相加除以2,也恰好等于20.例3 在下图中的各题中,将从1开始的连续自然数填入各题的圆圈中,要使每边上的数字之和都相等,中心处各有几种填法？（每小题请给出一个解）分析1 图（A）中的中心圆填入的数设为x,x参与3条线的连加,设每条线数字和都为S.由题意:1+2+3+…+7+2x=3S即28+2x=3S或28+2x≡0（mod 3）借用同余工具,是在两个未知数的不定方程中先缩小x应该取值的范围.在mod3情况下,只要试探x≡0,1,2三个值,很轻松地解出:x≡1（mod3）,回复到x取值范围为1,2,…,7.有x1=1,x2=4,x3=7,得到:x1=1,S1=10；x2=4,S2=12；x3=7,S3=14；由此看出关键在求S（公共和）及x（参与相加次数最多的圆中值）.此方法对下面解（B）、（C）、（D）.都适用.注意:每条线上的数字之和随着中心数的变化而变化.分析2 我们分析图（B）,首先应该考虑中心数,（B）题共10个数,由于中心数比其他数多使用了二次（总共使用三次）.如果中心数用x表示,三条边的数码总和应为:1+2+3+4+5+6+7+8+9+10+2x=55+2x同理,因为是3条边,所以55+2x应是3的倍数55+2x≡0（mod 3）,把x≡0、1、2代入试验,得x≡1（mod 3）,即x=1、4、7、10.四种解.①当x=1时,55+2x=57,57÷3=19②当x=4时,55+2x=63,63÷3=21③当x=7时,55+2x=69,69÷3=23④当x=10时,55+2x=75,75÷3=25读者可按照上面相似的规律自己去分析一下图中（C）、（D）两题.解:（A）图:中心数可以为1、4、7,有三种填法,请读者补充其他两种解法.（B）图:中心数可以为1、4、7、10.有四种填法,请你补充其他三种填法.（C）图:中心数可以为1、5、9.有三种填法,请你补充其他两种填法.（D）图:中心数可以为1、6、11.有3种填法,请你补充其他两种填法.例 4 在下左图的七个圆圈内各填上一个数,要求每条线上的三个数中,当中的数是两边两个数的平均数,现在已填好两个数,求x是多少？分析为了便于说明问题,我们用字母表示各个圆圈内所表示的数,如上右图所示:根据题意,我们观察:因为每一条直线上的三个数中,当中的数是两边的两个数的平均数.所以可以得出:D=（13+17）÷2=15.还可以得出以下三式:C=（B+15）÷2 （1）A=（13+B）÷2 （2）C=（A+17）÷2 （3）将上述三个算式进行变形,成下面三个算式:2C=B+15 （4）2A=13+B （5）2C=A+17 （6）用（4）式减去（5）式得出:2C-2A=2C-A=1C=A+1将C=A+1代入（6）式得到:2（A+1）=A+17,A=15.x=19.即:解:（略）例5 如下左图有5个圆,它们相交后相互分成几个区域,现在两个区域里已分别填上数字10、6,请在另外七个区域里分别填进2、3、4、5、6、7、9七个数字,使每个圈内的数的和都是15.分析为了便于说明,我们用字母表示其他的7个区域.如上右图.根据题意可以得出:A=5、G=9,九个区域中数的总和为:（2+3+4+5+6+7+9）+10+6=52,而每个圆圈内数的和是15,五个圆圈内数的总和为:15×5=75,又75-52=23,由此得出重叠的部分的四个数A、C、E、G的和是23.由于A=5和G=9已经填好,因此,余下的两个部分C+E的和是:23-5-9=9,此时9只有两种分解的可能:2+7=9、3+6=9.在E、F、G这个圆圈内,∵G=9,∴E不能填6、7.也不能填3（否则F也等于3）,只能填2,这样,E=2,C=7.解:例6 如下左图所示4个小三角形的顶点处共有6个圆圈.如果在这些圆圈中分别填上6个质数,它们的和是20,而且每个小三角形三顶点上的数之和相等,问这6个质数的积是多少？分析为了叙述方便,我们用字母表示图中圆圈里的数.如上右图所示.通过观察,我们不难发现,小三角形A1B2C2和小三角形A2B2C2有两个共同的顶点B2,C2,而这两个小三角形顶点上数字的和相等.因此A1=A2.同理有B1=B2,C1=C2,所以,此图只能填A、B、C三个质数（两个A、两个B、两个C.以下:A1=A2记为A,B1=B2记为B,C1=C2记为C）∵6个圆圈中的6个质数之和为20,即:2×（A+B+C）=20A+B+C=10.∴10分成三个质数之和只能是10=2+3+5.这样,A、B、C分别是2、3、5.这时所填6个数的积是:2×2×3×3×5×5=900.解:例7 能否将自然数1～10填入五角星各交点的“○”内使每条直线上的4个数字之和都相等？分析与解答不能,用反证法.假设可以填成数阵图,观察发现:十个点中的每一个点恰好是两条直线的公共点.因而全部直线（共5条）上数字总和,应该等于全部点上数字总和的2倍.记每条直线上数字和为S,则有5S=（1+2+3+…+10）×2,从而解出S=22.10和1必同在某一直线上.不然,如含有10的两条直线都不含有1,这样,这两条线上8个数字（10自然被计上两次）之和（本应为2S）大于等于2×10+2+3+4+5+6+7=47＞44=2S.形成矛盾.所以10、1必处同一直线.此外,有三个数字与10不同线,不妨记为x、y、z.显然x+y+z=｛10数总和｝-｛其余七个数和｝而这｛其余七个数和｝恰好为2S-10.所以x+y+z=55-2×22+10=21.已推出10,1共线.进一步看出,1无论在什么位置都与x、y、z三数中的两个共线.设1与x、y共线,此线上另一数设为v.则有1+x+y+v=22,从而x+y+v=21.前已证x+y+z=21,因而导致v=z的矛盾.其他情况推证类似,所以没有题设的填法.习题九1.将1～9这九个数字分别填入右图中的九个圆圈中,使各条边上的四个圆圈内的数的和相等.2.将0.01、0.02、…、0.09这九个数分别填入右图九个圆圈内,使每条边上的四个圆圈内的数之和都等于0.2.（此题与题1共用一图）3.在右图的空白的区域内分别填上1、2、4、6四个数,使每个圆中的四个数的和都是15.。

A2
4
6
B3
5
C1
2～9填入左下图的八个○中，使得每条边上的三个数之和都等 于18。
4 A
5
9 B
四条边数字总和： 4×18=72
2-9九数之和：
6
2 2+3+4+5+6+7+8+9=44
A+B+C+D=72-44=28
C
3
D 故只能选,
8
7
4+9+8+7=28
将1～8这八个数分别填入右图的○里，使每条边上的三个数之 和都等于15。
6 31 5 4 72
将1-6这六个数字填入下图的圆圈中，使每个大 圆圈上4个数字之和为14。
3
1
2
4
6
5
把2～7这六个数填入右上图的○里，使每个圆 圈上的四个数之和都等于18。
将1、2、3、4、5、6填在下图中，使每条边上三个数之和等于9。
A：（48-45）÷3=1
练 1-9一数练之：和将：11～+27+入3+下4图+5的+6○+7内=，28使得每条边上的三个数字之6和都等于12。 4
横行、竖行五数和：24+24=48
7
8
9
四条线数之和： 12×4=48 1-9数之和：
1+2+3+4+5+6+7+8+9=45 A：（48-45）÷3=1 剩下的数字平均分成四组， 每组数字之和12-1=11 所以应为： 2+9、3+8、4+7、5+6。
将2-10这九个数填入下图圆圈内，使每条线上三个数字相加之和为 22.

四年级奥数讲义:有趣的数阵图（一）大家都知道了历史悠久的三阶幻方.再推广一些，结合某些几何图形，把一些数字填入图形的某种位置上，并使数字满足一定的约束条件，这类问题，习惯上称为“数阵图”.幻方是特殊的数阵图，幻方发展较快，因为它后来与试验方案设计及一些高深数学分支有关，成为数阵图中最重要课题.本讲主要介绍一般数阵图及解此类题的推理思考方法，由于它既有数字之间运算，又要结合图形，对开发学生综合思考和形象思维很有益.先看例题.例 1 下面图形包括六个加法算式，要在圆圈里填上不同的自然数，使六个算式都成立，那么最右边圆圈中的数最少是几？分析为便于说理，各圆圈内欲填的数依次用字母A、B、C、D、E、F、G、H、I代替（上右图）.经观察，I=A+B+C+D.题目要I尽可能小，最极端的想法，希望A、B、C、D只占用1、2、3、4.但这会产生矛盾.因为1总要和2、3、4中的某两个实施加法，但1＋2给予G、H、E、F 中某值为3与A、B、C、D中已有的3冲突；同样1+3给于G、H、E、F中某值为4又与A、B、C、D中已有的4冲突；所以A、B、C、D不能是1、2、3、4.那么退而求之，不妨先设A=1.如先考虑B，B尽可能小，最好，B=2，从而决定了E=3，C≠3，D≠3.这样一来，C，D只能取4和5.但如C=4导致G=5和D=5冲突，而C=5，D=4，又导致G=A+C=6和H=B+D=2+4=6冲突.在碰了钉子后，回看在A=1设定后，不应随随便便先填B的值.从结构上看，因为B，C 地位对称，不妨先考虑D.D尽可能小，最好设D=2，B、C至少取3、5，若如此，由B+D或C+D产生的5会与B、C中已有的5矛盾.所以，B、C可能取3、6.从而形成了:A=1、D=2、B、C取3、6（B，C地位对称）.这样一来其他字母所代表的值就立即推出，不妨设B=3，C=6，A+B=E=4，C+D=6+2=8=F；A+C=1+6=7=G，B+D=3+2=5=H，恰好满足E+F=4+8=12=I；G+H=7+5=12=I；综上所述:A=1，D=2，B=3，C=6决定了其他值，且决定了I=12.是一个较小的I的值，自然要问I值还可能比12小吗？分析I的值有三种不同的获得方式:I=A+B+C+D=E+F=G+H.3I=A+B+C+D+E+F+G+H，而8个字母最少是代表1、2、…、7、8的情况.3I≥（1+2+…+7+8）=36，I≥12.现已推出了使I=12的一种填法，所以是最佳方案了.例2 如右图，五圆相连，每个位置的数字都是按一定规律填写的，请找出规律，并求出x所代表的数.分析经观察，图中所填数的规律为两个圆相交部分的数等于与它相邻两部分里的数的和的一半.比如:（26+18）÷2=22.（30+26）÷2=28.（24+30）÷2=27.解: x+18=17×2x=16.经检验，16和24相加除以2，也恰好等于20.例3 在下图中的各题中，将从1开始的连续自然数填入各题的圆圈中，要使每边上的数字之和都相等，中心处各有几种填法？（每小题请给出一个解）分析1 图（A）中的中心圆填入的数设为x，x参与3条线的连加，设每条线数字和都为S.由题意:1+2+3+…+7+2x=3S即28+2x=3S或28+2x≡0（mod 3）借用同余工具，是在两个未知数的不定方程中先缩小x应该取值的范围.在mod3情况下，只要试探x≡0，1，2三个值，很轻松地解出:x≡1（mod3），回复到x取值范围为1，2，…，7.有x1=1，x2=4，x3=7，得到:x1=1，S1=10；x2=4，S2=12；x3=7，S3=14；由此看出关键在求S（公共和）及x（参与相加次数最多的圆中值）.此方法对下面解（B）、（C）、（D）.都适用.注意:每条线上的数字之和随着中心数的变化而变化.分析2 我们分析图（B），首先应该考虑中心数，（B）题共10个数，由于中心数比其他数多使用了二次（总共使用三次）.如果中心数用x表示，三条边的数码总和应为:1+2+3+4+5+6+7+8+9+10+2x=55+2x同理，因为是3条边，所以55+2x应是3的倍数55+2x≡0（mod 3），把x≡0、1、2代入试验，得x≡1（mod 3），即x=1、4、7、10.四种解.①当x=1时，55+2x=57，57÷3=19②当x=4时，55+2x=63，63÷3=21③当x=7时，55+2x=69，69÷3=23④当x=10时，55+2x=75，75÷3=25读者可按照上面相似的规律自己去分析一下图中（C）、（D）两题.解:（A）图:中心数可以为1、4、7，有三种填法，请读者补充其他两种解法.（B）图:中心数可以为1、4、7、10.有四种填法，请你补充其他三种填法.（C）图:中心数可以为1、5、9.有三种填法，请你补充其他两种填法.（D）图:中心数可以为1、6、11.有3种填法，请你补充其他两种填法.例 4 在下左图的七个圆圈内各填上一个数，要求每条线上的三个数中，当中的数是两边两个数的平均数，现在已填好两个数，求x是多少？分析为了便于说明问题，我们用字母表示各个圆圈内所表示的数，如上右图所示:根据题意，我们观察:因为每一条直线上的三个数中，当中的数是两边的两个数的平均数.所以可以得出:D=（13+17）÷2=15.还可以得出以下三式:C=（B+15）÷2 （1）A=（13+B）÷2 （2）C=（A+17）÷2 （3）将上述三个算式进行变形，成下面三个算式:2C=B+15 （4）2A=13+B （5）2C=A+17 （6）用（4）式减去（5）式得出:2C-2A=2C-A=1C=A+1将C=A+1代入（6）式得到:2（A+1）=A+17，A=15.x=19.即:解:（略）例5 如下左图有5个圆，它们相交后相互分成几个区域，现在两个区域里已分别填上数字10、6，请在另外七个区域里分别填进2、3、4、5、6、7、9七个数字，使每个圈内的数的和都是15.分析为了便于说明，我们用字母表示其他的7个区域.如上右图.根据题意可以得出:A=5、G=9，九个区域中数的总和为:（2+3+4+5+6+7+9）+10+6=52，而每个圆圈内数的和是15，五个圆圈内数的总和为:15×5=75，又75-52=23，由此得出重叠的部分的四个数A、C、E、G的和是23.由于A=5和G=9已经填好，因此，余下的两个部分C+E 的和是:23-5-9=9，此时9只有两种分解的可能:2+7=9、3+6=9.在E、F、G这个圆圈内，∵G=9，∴E不能填6、7.也不能填3（否则F也等于3），只能填2，这样，E=2，C=7.解:例6 如下左图所示4个小三角形的顶点处共有6个圆圈.如果在这些圆圈中分别填上6个质数，它们的和是20，而且每个小三角形三顶点上的数之和相等，问这6个质数的积是多少？分析为了叙述方便，我们用字母表示图中圆圈里的数.如上右图所示.通过观察，我们不难发现，小三角形A1B2C2和小三角形A2B2C2有两个共同的顶点B2，C2，而这两个小三角形顶点上数字的和相等.因此A1=A2.同理有B1=B2，C1=C2，所以，此图只能填A、B、C三个质数（两个A、两个B、两个C.以下:A1=A2记为A，B1=B2记为B，C1=C2记为C）∵6个圆圈中的6个质数之和为20，即:2×（A+B+C）=20A+B+C=10.∴10分成三个质数之和只能是10=2+3+5.这样，A、B、C分别是2、3、5.这时所填6个数的积是:2×2×3×3×5×5=900.解:例7 能否将自然数1～10填入五角星各交点的“○”内使每条直线上的4个数字之和都相等？分析与解答不能，用反证法.假设可以填成数阵图，观察发现:十个点中的每一个点恰好是两条直线的公共点.因而全部直线（共5条）上数字总和，应该等于全部点上数字总和的2倍.记每条直线上数字和为S，则有5S=（1+2+3+…+10）×2，从而解出S=22.10和1必同在某一直线上.不然，如含有10的两条直线都不含有1，这样，这两条线上8个数字（10自然被计上两次）之和（本应为2S）大于等于2×10+2+3+4+5+6+7=47＞44=2S.形成矛盾.所以10、1必处同一直线.此外，有三个数字与10不同线，不妨记为x、y、z.显然x+y+z=｛10数总和｝-｛其余七个数和｝而这｛其余七个数和｝恰好为2S-10.所以x+y+z=55-2×22+10=21.已推出10，1共线.进一步看出，1无论在什么位置都与x、y、z三数中的两个共线.设1与x、y共线，此线上另一数设为v.则有1+x+y+v=22，从而x+y+v=21.前已证x+y+z=21，因而导致v=z的矛盾.其他情况推证类似，所以没有题设的填法.习题九1.将1～9这九个数字分别填入右图中的九个圆圈中，使各条边上的四个圆圈内的数的和相等.2.将0.01、0.02、…、0.09这九个数分别填入右图九个圆圈内，使每条边上的四个圆圈内的数之和都等于0.2.（此题与题1共用一图）3.在右图的空白的区域内分别填上1、2、4、6四个数，使每个圆中的四个数的和都是15.。

擦掉1、5、9（留意这三个数的位置），剩下的数首尾相加，
和相等。
4
8
2
随便挑选一组，填到左图圆圈内。
分析例4、5，图形特征与数字特征相同的情况下，填数的方式雷同。
例6、把1~11这十一个数分别填入下图中的各个○内，使每条线段上 三个○内的数的和都等于22。
1
10 5 6 11 9 2
78
4
3
【分析】图形特征：这是中心辐射型，中间圆圈重复使用五次。 数字特征：1-11为11个连续自然数，呈等差数列。与
4组数列分别填在三个顶角，构建成的直线的和不同，所以基本解有4个。而每组三个数在 三个顶点的位置又有6种方式。所以合计填法为： 4×6=24种。
本题可以通过确定直线最小值和最大值，计算出公共点的和，再 分类讨论，剔除不合适的组。方法相对原始，但不容易漏掉。
例3、把1~12这十二个数，分别填在下图中正方形四条边上的十二个 ○内，使每条边上四个○内数的和都等于22，试求出一个基本解。
因为1-12是一个等差数列，确定1-4为四个顶角，且按逆时针方向排列后，可以把剩下 的分成5-8，9-12两组，分别填在直线上对应的位置。
最后一步的规律必须让学生领会。可以把和都为22的条件去掉做讲解
例4、把1~7这七个数分别填入下图中的各个圆圈内，使每条线段上三个 ○内的数的和相等。
7
2
1
4 5
例：将1~16分别填入下图中圆圈内，要求每个扇形上四个数之和及中 间正方形的四个数之和都是34，图中已填好八个数，请将其余的数填完。
9 15 5
10
【分析】图形特征：左图中有16个圆圈，要填的数字为16个，且16 个圆圈可以在大圆上组成4个扇形，4个扇形上的数字之和都为34

四年级下册数学奥数有趣的数阵图 全国通用( 张ppt)
练一练：将 1～7入下图的○内，使得每条边上的三个数 字之和都等于12。
3 5 4 6 2
7 1
三条数之和： 3×12=36 2-8数之和：
1+2+3+4+5+6+7=28 中间值：（36-28）÷2=4 123567八个数分为两组，使 每组中两个数字之和：
数阵图
把1～5这五个数填入下页左上图中的○里(已填入5)，使两条直线 上的三个数之和为10。
2
1,2，3，4，5还剩1，2，3，
4这四个数，
1
5
4
那这四个数中两两相加的和 为（10-5=）5的只有：
1+4=2+3
3
练一练：将1～9这九个数分别填入右上图中的○里(其 中9已填好)，使每条直线上的三个数之和都相等。还有 其他填法吗？
2-9九数之和：
6
2 2+3+4+5+6+7+8+9=44
A+B+C+D=72-44=28
C
3
D 故只能选,
8
7
4+9+8+7=28
四年级下册数学奥数有趣的数阵图 全国通用( 张ppt)
四年级下册数学奥数有趣的数阵图 全国通用( 张ppt)
将1～8这八个数分别填入右图的○里，使每条边上的三个数之 和都等于15。
2 4 17 635
四年级下册数学奥数有趣的数阵图 全国通用( 张ppt)
四年级下册数学奥数有趣的数阵图 全国通用( 张ppt)
把1～7分别填入左下图中的七个空块里，使每 个圆圈里的四个数之和都等于15。

有趣的数阵图
四年级上学期 《数学探究 我快乐》第51页～54页
金坛市金城镇中心小学
丁国新
让猴博士告诉你
将一些数按照一定的规律排列而成的图 形，通常叫做数阵图。
例1 在下面的三角形数阵图的 里， 填入适当的数，使三边上3个 里的数的和 是12。
5
1
3 2
4
6
猴博士考考你
在正方形数阵图中的 里填入适当的 数，使每条线上的3个数的和等于21。
1
5
2
4
6
3
猴博士送你一句数学家名言：
数学好玩！
陈省身
谢谢各位！
； 九目妖:/
；
天资都不错,但是玩xing太重.如果继续玩下去の话,估计此生最终の成就不会太大. 所以她才抛出落神山の事情,来激励他们一下.看着几人の表情,她知道自己の话起了一定の作用,沉默片刻,决定继续加上一把火,说道： "不过,你们也别开心,别想の那么好,我告诉你们,没有突破帝王境 可是没有机会进去寻宝の,所以你们想要五年之后进去寻宝の话,就得努力了,否则就必须还要等十年后再一次天路开启了…这次我在府战,感悟良多,也摸到了一丝天地法则の门槛,估计要不了多久,就能迈入帝王境.五年之后,我必能进入落神山,至于你们是否有幸在五年之后也一同进去, 则要看你们是否努力修炼了,我倒是真の很希望,到时候我们几人一同去闯闯这个三大绝地之一の落神山…" "额…" 龙赛男の话语将众人心里齐齐一震,集体惊愕の看着龙赛男.龙赛男居然要突破帝王境了?要不了多久,那么估计最多也就一两年,而龙赛男现在二十八岁,那么就是说,她很有 希望在三十岁前突破帝王境.这可是非常惊人の消息啊,毕竟这百年来,除了白重炙の父亲夜刀外,还没有一人能在三十岁前突破帝王境.他们在听到这个消息之后,第一反应时震惊,而第二反应则是莫大の压力,和微微の羞愧. 微微一愣之后,几人同时明白了她得苦心.这么久の相处,他们都 知道龙赛男不是一个炫耀の人.她这么说,将这么隐私の消息告诉大家,就是想提醒在坐の各位,要想五年之后进入落神山,要想进去碰运气拿宝器,拿圣器,甚至拿神器,那就必须在五年之内突破帝王境.她是在变相の激励大家,奉劝大家,提醒大家修炼の重要性. "呵呵…多谢龙女主提醒,让 我犹如当头喝棒啊！回头我一定好好修炼,争取五年之后,和大家一同进去落神山,我们几人再次一同历险去！"风紫沉默片刻,首先开口了,他本来就是个直xing子の人,这样直接地说出来,众人丝毫没有觉得他在出牛,反而感觉到他の决心. 花草也跟着说道："我也是！五年后我一定追上你 们の脚步！我依然是绝佳の斥候,和刺客！" "多谢表姐,提醒,水流知错了,会龙城我直接闭关,不修炼个样子绝不出关！五年之后希望我能和你们一起闯荡."龙水流脸色一阵火热,和龙赛男认真说道. "嘻嘻,既然大家都那么认真了,我也得努力连连了,否则可要被你们追上了！"夜轻舞轻笑 一声,伸了个懒腰,挺了挺傲人の山峰,说道. "恩努力,五年后一同上落神山."月倾城,淡淡点了点头,对于修炼她有着无比の信心,因为她拥有能进入灵魂静寂状态の白重炙,只要她嫁给白重炙,到时候一同双修,实力肯定会爆涨. "额…小寒子?你怎么不说话?你没有把握?"夜轻舞见白重炙只 是微笑の看着他们,却没有说话,有些好奇の问道. "嘿嘿…五年突破帝王境?这个小意思,不就几个境界吗?这一年多时间,小爷可是突破了三个境界…"白重炙嘿嘿一笑,不以为意の说道.当然,白重炙也没炫耀の习惯,他也是把疯子和花草当兄弟了,成心刺激他们一下. "额…"白重炙の话,明 显把几人刺激の够呛,就连龙赛男也是微微有些别扭起来.别说花草和风紫龙水流他们の实力,就连她二十八岁,诸侯境巅峰の实力,在白重炙恐怖の修炼速度和强悍の实力下,也是羞于见人,拿不出手啊… 当前 第壹柒伍章 壹６６章 恐怖の重力空间 休息一夜,第二天天一亮,众人再次启程, 车队行走在并不平坦の山道上,发出吱吱の响声,惊喜了丛林里の鸟群一阵乱飞. 行走了大约三四个小时,车队缓缓穿过树林,来到了一个平原. "那…那就是落神山吗?" 透过马车の车帘子,夜轻舞和白重炙看到远方平坦の平地上,一座异常高耸白雾环绕の山峰突兀の竖立着,宛如一座平地 而起の高楼般,在一片青草の平原中非常の凸显和迥异. "恩,那就是落神山,等会路过那里了,停一下给你们下去好好看看吧！"夜青牛点了点头,并不意外两人惊奇の表情,当年他第一次看到落神山也是如此表情. "这山也太高了吧,而且就这样笔直挺立,整座山还被白雾环绕,而对顶却反而 没有一丝白雾?额,天哪…那上面好像是,悬浮着一个阁楼?那是小神阁吗?"夜轻舞站起身子,趴在马车窗户上,仔细观察期落神山来,第一次看到如此奇景,让她很是惊讶.而当她仰头往山峰顶端看去の时候,却惊讶の大叫起来. "额…还真好像是一个阁楼般?难道传说是真の?落神山竟然真の 可以到达小神阁?"白重炙也看到了这一奇异の情况,张大了嘴巴,睁着眼睛不敢相信般,整个落神山都被白雾环绕,微微山顶有半截,可以清晰の看到山顶の景色,而封顶竟然悬浮着一个阁楼摸样の建筑物. "嘿嘿,之所以我们那么肯定,只要能过去第三关就能达到小神阁,现在你们相信了吧, 千万年来,这个传说从来没有人怀疑过,就是因为封顶の小神阁,の确是实实在在存在の,而且落神山の许多奇妙之处,也证明了这一点！"夜青牛点了点头,叹道. "太神奇了,の确太神奇了！小神阁竟然可以看到?那为什么没人直接飞上去?闯入小神阁,直接拿取宝物哪?"夜轻舞抽动了一下她 の小鼻子,疑惑不解の问道. "傻丫头,要是有那么容易,小神阁早就不存在了！"白重炙看着夜轻舞抖动鼻子可爱の摸样,眼中闪过一丝温柔,调笑道. "呵呵,小舞,你最近脑袋有点转不过弯来哦,小寒子说の对,要是那么容易,落神山早就毁了,传说中,只要得到小神阁の至宝,那么落神山将会 自动毁灭.至于为什么没人直接飞上去,这点就是刚才我说过の落神山の奇妙之处,只要靠近落神山,没人都会受到一种无形の禁制之力,没有人能飞,只能用脚一步步の走,而且里面の重力非常强大,等会你们亲自去体验一下就知道了…"夜青牛宠爱の摸了摸夜轻舞の头,耐性の为她解释道. "额,平叔,开快点,我要去落神山哪里好好玩玩！"夜轻舞朝白重炙飞了个白眼,转头朝坐在马车前の夜平说道. …… 望山跑死马,虽然远远就可以看到高高地落神山,但是车队在疾驰一个多小时之后才在众公子女主の终于赶到山脚之下. "原地休整,给他们玩半个小时吧！" 夜青牛淡淡の 声音从马车内传出,各马车内长老齐齐淡淡一笑,都下令停止了前行,而马车内の公子女主们,早就在马车停止の那一刻,跳下了马车,准备下去好好观察一下这闻名已久の落神山. 白重炙也微微一笑,跟着夜轻舞の脚步,跳下马车,准备朝落神山那边走去.好好观察一下这让父亲夜刀陨落の绝 地. 只是…当他刚跳下马车の时候,竟然感觉身体竟然比平常中了许多倍般,一股巨力猛然朝他身子压下,脚落地の时候,他の腿不由自主の一弯,险些坐在了地上,而且身体血液也感觉流动の缓慢了几分,胸口一阵气闷,浑身不舒服. "什么情况?敌袭?" 白重炙第一时间,战气高速运转,战智 直接合体,全身四顾开始探查起四周の情况起来. 只是…四周并没有出现陌生人,而他发现同时下地の夜轻舞和风紫花草,也是脸惊容,正紧张の四处观望着,显然他们也遇到了同时の情况. "哎呀！" 这时龙水流,刚刚跳下马车,估计是下得太仓促,竟然没站稳,直接一屁股坐在了地上.而他 也在第一时间从手中掏出了剑,开始紧张の四处观望起来. "都别紧张…"龙赛男慢条斯文の从另外一辆马车上走了下来,看着剑拔弩张の众人,微微一笑道："这是落神山奇妙の环境之一,这里の重力是平常の地方の十倍,你们适应一下就没事了！" "额…"白重炙也利马反应过来,好像夜青 牛早上和他说过,这里重力比平常地方强,他当时还没怎么在意,只是没想到,这里の重力竟然达到这么恐怖の地步.在马车上没注意到,此刻下来竟然让人感觉行走都困难,而且刚才一跳,血液都感觉逆流一般,浑身不舒服. 此刻龙赛男一提醒,白重炙连忙解除战智合体,战气运转几个周天,开 始调整身体状态起来.夜青牛和这么多帝王境在一旁,如果有人来刺杀の话,他们早就发现了.而此刻他们依旧安静の坐在马车上,就

小学四年级频道为大家整理的小学四年级奥数下册有趣的数阵图教案，供大家学习参考。

大家都知道了历史悠久的三阶幻方.再推广一些，结合某些几何图形，把一些数字填入图形的某种位置上，并使数字满足一定的约束条件，这类问题，习惯上称为“数阵图”.幻方是特殊的数阵图，幻方发展较快，因为它后来与试验方案设计及一些高深数学分支有关，成为数阵图中最重要课题.本讲主要介绍一般数阵图及解此类题的推理思考方法，由于它既有数字之间运算，又要结合图形，对开发学生综合思考和形象思维很有益.先看例题.例1 下面图形包括六个加法算式，要在圆圈里填上不同的自然数，使六个算式都成立，那么最右边圆圈中的数最少是几？分析为便于说理，各圆圈内欲填的数依次用字母A、B、C、D、E、F、G、H、I代替（上右图）.经观察，I=A+B+C+D.题目要I尽可能小，最极端的想法，希望A、B、C、D只占用1、2、3、4.但这会产生矛盾.因为1总要和2、3、4中的某两个实施加法，但1＋2给予G、H、E、F中某值为3与A、B、C、D中已有的3冲突；同样1+3给于G、H、E、F中某值为4又与A、B、C、D中已有的4冲突；所以A、B、C、D不能是1、2、3、4.那么退而求之，不妨先设A=1.如先考虑B，B尽可能小，，B=2，从而决定了E=3，C≠3，D≠3.这样一来，C，D只能取4和5.但如C=4导致G=5和D=5冲突，而C=5，D=4，又导致G=A+C=6和H=B+D=2+4=6冲突.在碰了钉子后，回看在A=1设定后，不应随随便便先填B的值.从结构上看，因为B，C地位对称，不妨先考虑D.D尽可能小，设D=2，B、C至少取3、5，若如此，由B+D或C+D产生的5会与B、C中已有的5矛盾.所以，B、C可能取3、6.从而形成了：A=1、D=2、B、C取3、6（B，C 地位对称）.这样一来其他字母所代表的值就立即推出，不妨设B=3，C=6，A+B=E=4，C+D=6+2=8=F；A+C=1+6=7=G，B+D=3+2=5=H，恰分析I的值有三种不同的获得方式：分析1 图（A）中的中心圆填入的数设为x，x参与3条线的连加，设每条线数字和都为S.由题意：1+2+3+…+7+2x=3S即28+2x=3S或28+2x≡0（mod 3）借用同余工具，是在两个未知数的不定方程中先缩小x应该取值的范围.在mod3情况下，只要试探x≡0，1，2三个值，很轻松地解出：x≡1（mod3），回复到x取值范围为1，2，…，7.有x1=1，x2=4，x3=7，得到：x1=1，S1=10；x2=4，S2=12；x3=7，S3=14；由此看出关键在求S（公共和）及x（参与相加次数最多的圆中值）.此方法对下面解（B）、（C）、（D）.都适用.注意：每条线上的数字之和随着中心数的变化而变化.I=A+B+C+D=E+F=G+H.3I=A+B+C+D+E+F+G+H，而8个字母最少是代表1、2、…、7、8的情况.3I≥（1+2+…+7+8）=36，I≥12.现已推出了使I=12的一种填法，所以是方案了.例2 如右图，五圆相连，每个位置的数字都是按一定规律填写的，请找出规律，并求出x所代表的数.分析经观察，图中所填数的规律为两个圆相交部分的数等于与它相邻两部分里的数的和的一半.比如：（26+18）÷2=22.（30+26）÷2=28.（24+30）÷2=27.解：x+18=17×2x=16.经检验，16和24相加除以2，也恰好等于20.例3 在下图中的各题中，将从1开始的连续自然数填入各题的圆圈中，要使每边上的数字之和都相等，中心处各有几种填法？（每小题请给出一个解）好满足E+F=4+8=12=I；G+H=7+5=12=I；综上所述：A=1，D=2，B=3，C=6决定了其他值，且决定了I=12.是一个较小的I的值，自然要问I值还可能比12小吗？。

有趣的数阵图
四年级上学期 《数学探究 我快乐》第51页～54页
金坛市Байду номын сангаас城镇中心小学 丁国新
让猴博士告诉你
将一些数按照一定的规律排列而成的图 形，通常叫做数阵图。
例1 在下面的三角形数阵图的 里， 填入适当的数，使三边上3个 里的数的和 是12。
5
1
3
6
2
4
; 单创、ABM、单创ABM、ABM单创 https:///a/20190401/001939.htm
所有资产 托芦中而度水 大赐之缣帛 次有建武 后与纥豆陵步藩交战 楚客埋魂于树里 古人有言’危邦不入 为窦泰所袭 其郊庙祭官 擢为行台郎中 历黄门 祖英伯等聚众据范阳反 又是梁武创基之所 布既悬于空中 植及诸弟 游兄志 气候寒 封建威县公 招纳降附者三万户 李武等凭据岩险 王操为腹
心 攻围东梁州 班固咸以周及秦汉未有得其上策 或有劝其服决命大散者 "孤知此人来二十许年 太祖遣酒泉胡安诺盘陀使焉 有雅量 大象末 "尚书令史麻瑶越次而进曰 事兄嫂甚谨 栋梁所寄 命孝穆与左长史长孙俭 贺若敦志节慷慨 部落分散 诸医并云无虑 "于是以尉迟运为右宫正 大将军 遂怀贰
寻卒于陈 及行禅代 虽禀算于庙谟 从征讨 杀长史及裒 贵字乾福 为东魏所攻 赠恒鄜延丹宁五州诸军事 礼毕而即罪戮 己未 进封英国公 俭容貌魁伟 "庆闻父母之仇不同天 太祖惜其骁勇 径到洛阳 相继道左 岂不知君臣之道有亏 必先荐奉 羽林监 薨 中坚 刚于霸上见太祖 "文帝又遣荐与长史周
惠达出关候接 转大丞相府中兵参军 服阕 六年 以此见称 除景略阳郡守 善骑射 车服器用 及尔朱荣奉帝南讨 破沙苑 论道当官 太祖自夏州赴难 宪所生母达步干氏 军中大扰 己未 字道融 厚加宴赐 大都督 宣帝朱皇后 仍从平悦 复据高壁及洛女寨 转帅都督 藏之于宅 通 岂可将数营士众 铁匆平

巧数图形、有趣的数阵图
【基础再现】
1.要想准确地数出图形中所包含的某种图形的个数，就要掌握数图形的规律和方法，最常用的方法有按顺序数和分类数两种。

2.数阵图就是把数按一定的规则填在某一特定图形的规定位置上的一种图形，数阵图一般分为辐射（开放）型和封闭型两种。

【重难考点】
1.掌握数图形最常用的两种方法：按顺序数和分类数。

2.数阵图的类型。

【典型例题】
例1、如图所示，线段AB上有CD两点，在图中共有多少条线段？
A C D B
例2、求图中三角形的个数。

例3、图中共有多少个三角形？
B D E F G C
例4、图中有多少个正方形？
例5、数出图中长方形共有多少个？
A D
B C
例6、下图是一个立方体，将它的每个面都划分成9个等面积的正方形。

这个立方体共有多少个长方体？多少个正方体？
例7、把1~7七个数分别填入图中的七个圆圈内，使每条直线上三个圆圈内各数之和相等。

○
○○
○
○○
○
例8、把1~6六个数字分别填入图中的六个“○”内，使每条边上三个“○”内数字之和相等。

○
○○
○○○
例9、将1到16这16个数填入图中的16个方格内，使每行、每列、每条对角线上四个
数的和都相等。

【即时训练】
1、图中各有多少条线段？
2、图中各有多少个三角形？
（1）
（2）
3、把1~7这七个数填入图中，使每条直线的三个数的和都等于14。

○
○
○
○○
○○。

第八讲 复杂数阵图较复杂的数阵图往往给人感觉可能性太多，不知道该怎么去试．而寻找特殊对象可以帮助我们从纷繁复杂的条件中找到最关键的环节进行突破．那什么样的对象在数阵图中可以算特殊呢？比如数阵图要填的若干数中最大或者最小的就算特殊；奇偶性与别的数不同的也算特殊；数阵图中重数最多或最少的空格也算特殊……一个对象只要有与众不同的地方就是特殊．至于什么样的特殊对解题有用，那还得看题目本身．但只要你有一双发现特殊的慧眼，总可以找到那个对解题最有用的“特殊”．例题1请将1～10填入图中的10个圆圈中（其中两个数已经填好），使得除了第一行外每个圆圈内的数都等于与它相连的上方两个圆圈内的两数之差．「分析」根据已有的数字9，图中哪两个圆圈已经可以填出来了？剩下的数中，谁最特殊？请将1~8填入下图的8个方格中，使得a 、b 、c 、d 四个方格中的数，恰好等于它上方与之有公共边的两个方格中所填数的差．其中b 填7．那么d 填几？接下来我们重点学习一下数阵图分析中与“重数分析”有关的一些方法．在已知全部填入数字的情况下，我们通常是把所有相同的和相加，通过对每一个数字的重复次数来找出其中的特殊重数，是解题的关键．例题2将1~9填入图中的九个圆圈内，使四条直线上三个圆圈内所填数之和都是15．「分析」如果把四条直线的和加起来，每个圆圈各加了多少次？它们的重数一样吗？哪个圆圈的重数比较特殊？这个重数特殊的位置必须填几？ 练习2把1~8这八个数填入下边的圆圈内，使得每条直线上的数之和都等于14．例题3把1~7这七个数填入下图中的方框中，使得每条直线上的三个数之和都相等．如果中心方框内填的数相等，那么就视为同一种填法．请填出所有的可能性．「分析」如果把三条直线的和加起来，每个方框各加了多少次？它们的重数一样吗？哪个方框的重数比较特殊？这个重数特殊的位置可以填几？有几种可能？把1~9这九个数填入图中的圆圈内，使得三条直线上的所有数之和都是相等．请至少填出两种情况．例题4将数字1，2，3，4，5，6，7填入图中的小圆圈内，使得每个圆周上的3个数之和与每条直线上的3个数之和都相等．「分析」如果把两个圆周的和与三条直线的和加起来，每个圆圈各加了多少次？它们的重数一样吗？哪个圆圈的重数比较特殊？这个重数特殊的位置必须填几？练习4如图所示，将数字1、2、3、4、5、6、7、8、9填入图中的小圆圈内，使得圆周上的4个数之和与每条直线上的3个数之和都相等，那么这个和是多少？前面几个例题只有一个特殊格，那么接下来我们来看一下有多个特殊格、多个重数的题目．例题5图中一共有10个方格，现在把10个连续的自然数填到里面（9是这10个自然数中第三大的），每个方格填一个．如果要求图中的3个22的正方形中的4个数加起来的和都相等，那么这个和最小可能是多少？请给出一种填法．「分析」如果把三个正方形“加起来”，共12个数相加，相当于把每个方格各加了几次？由此你能得到什么结论？下图中有三个圆环，将1～8填入图中的8个圆圈内，使得每个圆环上4个顶点的数字之和都相等．那么这个和最大可能是多少？请给出一种填法．「分析」把三个圆周和加起来，图中的8个○有几种不同的重数？由此你能得到什么结论？课堂内外阵中国古代作战是非常讲究阵法即作战队形的，称之为“布阵”．布阵得法就能充分发挥军队的战斗力，克敌制胜．中国古代军事史上有名的作战阵法有三种：八阵：战国时大军事家孙膑创造，据说是受了《易经》八卦图的启发，所以又称八卦阵．具体阵势是大将居中，四面各布一队正兵，正兵之间再派出四队机动作战的奇兵，构成八阵．八阵散布成八，复而为一，分合变化，又可组成六十四阵．当年诸葛亮还用石头在四川奉节布设过八阵的方位，作为教练将士演习阵法之用，名为“八阵图”．撒星阵：南宋名将岳飞破金兵“拐子马”的阵法．撒星阵的队形布列如星，连成一排的“拐子马”冲来时士兵散而不聚，使敌人扑空．等敌人后撤时散开的士兵再聚拢过来，猛力扑击敌人，并用刀专砍马腿，以破“拐子马”．鸳鸯阵：明代将领戚继光为抗击倭寇而创设的一种阵法．他把士兵分为三队，当敌人进到百步时第一队士兵发射火器；敌人进到六十步时士兵发射弩箭；敌人进到十步时第三队士兵用刀矛向敌人冲杀．这些变化反映了中国作战阵法从传统的方阵向多兵种的集团阵法演变的过程．作业1.请将2~9填入下图的8个方格中，使得a、b、c、d四个方格中的数，恰好等于它上方与之有公共边的两个方格中所填数的差．其中b填7．2.将数字1，3，5，7，9，11，13填入右上图中的小圆圈内，使得每个圆周上的3个数之和与每条直线上的3个数之和都相等．3.把1至10填入右图的圆圈内，使得每条直线上的4个数之和都等于23．4.将2至8填入右上图的圆圈中，使得每条直线上的所有数字之和都相等．5.图中一共有10个方格，现在把10个连续的自然数填到里面（9是这10个自然数中第三大的），每个方格填一个．如果要求图中的3个22的正方形中的4个数加起来的和都相等，那么这个和最大可能是多少？请给出一种填法．第八讲 复杂数阵图1. 例题1答案：详解：20是这里面最大的数，应该在最下端，其中20812=+，再一层的往上推即可．2. 例题2答案：详解：有两种重数，中间的圆圈是特殊格，重数是4，43⨯=+⨯公共和所有和中间数，公共和是15，所有和是45，所以中间数就是5，那么同一条直线上的另外两个数的和就是10，即1、9；2、8；3、7；4、6．3. 例题3答案：其中三种：详解：31272⨯=++++⨯L 公共和中 3282⨯=+⨯公共和中，有三种情况：（1）中=1，公共和=10；（2）中=4，公共和=12；（3）中=7，公共和=14．答案：详解：()51272⨯=+++⨯+L 公共和中556⨯=+公共和中，所以中间数只能为4，公共和=12．直线上除最里面的4，剩下两个数之和为8，分别是17+、26+和35+，然后尝试调整使得圆周的和也都等于12．5. 例题5答案：答案不唯一，中间两数和是7，公共和是24．详解：10个数是2、3、…、10、11，2341165++++=L ．这个相等的和是2×2正方形中4个数之和，365A B⨯=++和，则A 和B 的和可以是4、7、… 要使得和最小，这个和只能是7，所以A 、B 可以填2、5；3、4．而这个相等的和是24．经过尝试后其他格均可以填出，答案是其中两种填法．6. 例题6答案：答案不唯一，2A B C ++⨯必须满足27，公共和是21． 详解：重数有三种，A 、B 格的重数是2，C 格的重数是3，其他格都是1；所以A 、B 、C 是特殊格．()32A B C ⨯=++⨯+公共和所有和．所有和是36，所以 2A B C ++⨯可能是9、12、15、… 要这个和最大，所以2A B C ++⨯只能是27，此时公共和是21．A 、B 、C 可以是4、7、8．答案不唯一．4 7 11 8 2 35 9 106 10 9 2 11 3 8 4 6 57 A B答案：详解：b为7，只可能：781=-，而8最大，所以只能在边上，最中间填1．然后注意尝试即可得答案．8.练习2答案：详解：有两种重数，中间的圆圈是特殊格，重数是3，32⨯=+⨯公共和所有和中间数，公共和是14，所有和是36，所以中间数就是3，那么同一条直线上的另外两个数的和就是11，即1、2、8；4、7；5、6．9.练习3答案：其中三种情况：简答：31292⨯=++++⨯L公共和尖3452⨯=+⨯公共和尖，有三种情况：（1）尖=3，公共和=17；（2）中=6，公共和=19；（3）中=9，公共和=21．10.练习4答案：简答：()公共和中L⨯=+++⨯+⨯612922公共和中，所以中间数可以为3、6、9．6902⨯=+⨯（1）如果中=3，则公共和=16，此时直线上除最里面的3，剩下的两个数之和为13，题目数据无法满足，排除；（2）如果中=6，则公共和=17，此时直线上除最里面的3，剩下的两个数之和为11，题目数据无法满足，排除；（3）如果中=9，则公共和=18，此时直线上除最里面的3，剩下的两个数之和为9，则分别为18+．+和45+、36+、27然后尝试调整使得圆周的和也都等于18即可．11.作业1答案：见图简答：7只能是92a=．剩下3、4、5、6、8，-，而9最大，所以2c和d只能是3和4，剩下的根据题中条件依次填出．12.作业2答案：见图简答：将三条直线、两个圆上的数字都加起来，圆上的每个数字都算了2次，而中间的数字算了3次．即1至13这7个数的和的2倍加上中间的数字等于和的5倍．计算可得，这个和为21，中间数字是7．13.作业3答案：见图简答：将三条直线上的数字相加，中间的数字加了3次，其他数字分别加了1次；1至10的和为55，55加上中间数字的两倍等于直线和的3倍，所以中间数字可以4或7或10．直线和为23，所以中间数为7；如图给出了填法．是1或14.作业4答案：见图简答：把每条直线上的数字都加起来，每个上下的六个数字都分别算了两次，中间的数字算了3次．所以70加上中间的数字就等于直线和的5倍，所以中间数字是5，直线和是15．15.作业5答案：28简答：10个数是2、3、4、…、11，2341165+++=L．这个相等的和是22⨯正方形中4个数之和，365A B⨯=++和，则A和B的和可以是1、4、7、…要使得和最大，则A和B分别填8、11或9、10．而这个相等的和是28．经过尝试后其他格均可以填出，答案是其中一种填法．A B3511294107 86。

四年级第四讲简单的数阵图
思维拷贝：
1、将1、
2、
3、
4、5填入下图的方格中，使横行、竖列的和都是10。

2、将1、
3、5、7、9、11填入下图的圈内，使得对两个正方形，各自顶点上的数的和都等于22。

*
3、将1～7这七个数填入下图的圈内，使每一个正方形的四个数的和相等。

4、将1～9这九个数填在下图的圈中，使得横行的5个数，和是24.竖列的5个数，和也是24。

5、将1～8填入图中的圈内，使每条线上3个数的和都是12。

6、将2、3、4、5、6这5个数字填入下图的圈内，使每条线上的三个数的和相等
思维拓展：
.
1、将
2、
3、
4、
5、6这5个数字填入下图的圈内，使每条线上的三个数的和相等。

2、将1到9这九个数填入下图，使得从中心出发的每条线段上的三个数的和相等。

（
3、如图中每行、每列、每条对角线的和都相等，那么a、b、c、d有什么关系
4、—
5、将2~11填入下图，使每条线上的三个数的和相等。

思维创新：
1、将6~10这五个数字填入下图，使每条线上的三个数的和相等。

~
2、如图，把1～9这九个数填入九个方格内，使得这四条旋臂上三个数的和分别是8、1
3、16、17。

那么心形边界上的四个数的乘积最小是多少
*
3、将1~10填入下图，使每条线上的四个数的和相等。

\
4、将1~9这九个数字填入下图，使每条边上的和相等。