有趣的数阵图

1+2+3+4+5+6+7=28 A：（30-28）÷2=1 134567八个数分为两组， 使每组中两个数字之和：
10-1=9 则2+7=3+6=4+5
有趣的数阵图
5
练一练：将 1～7入下图的○内，使得每条边上的三个数 字之和都等于12。
通关小诀窍：确定中间值
3 5
4
6
7
1 2
三条数之和： 3×12=36 2-8数之和：
有趣的数阵图
9
将2-10这九个数填入下图圆圈内，使每条线上三个数字相加之和为 22.
2
3
4
5
1A0
6
7
8
9
有趣的数阵图
10
将1、2、3、4、5、6填在下图中，使每条边上 三个数之和等于9。
1A
6
5
B2
4
3C
三条边数字总和： 3×9=27
1-6六数之和： 1+2+3+4+5+6=21
A+B+C=27-21=6 故只能选1，2，3
有趣的数阵图
14
把1～7分别填入左下图中的七个空块里，使每 个圆圈里的四个数之和都等于13。
2 4 17 635
有趣的数阵图
15
把1～7分别填入左下图中的七个空块里，使每 个圆圈里的四个数之和都等于15。
6 31 5 4 72
有趣的数阵图
16
将1-6这六个数字填入下图的圆圈中，使每个大圆 圈上4个数字之和为14。
50-45=5 12346789八个数分为两组， 使每组中四个数字之和：
25-5=20 则1+4+6+9=2+3+7+8

8
6
3
7
2
4
5
9
把1—8这8个数，填入下图中的八个○内，使 每条线段上的四个数的和，与每个四边形 四个顶点上的四个数的和都相等。 3 2 1 4 8 7 5 3 1 7 2 8 6 5
6
4
例题五 将1～7这七个数分别填入下图 的○里，使得每条直线上三个数之和与 每个圆圈上的三个数之和都相等。 7 1 4 5 3 6 2
• 1、将1、2、3、4、5、6六个数字填入图中 的小圆圈内，使每个大圆上四个数字的和 是16。
4
5 6
3 2
1
• 2、 将1—8这八个数，分别填入图中两个 圆圈的八个 ○内，使每个圆圈上五个 ○ 内数的和分别为20、21。 2 6 8 3 7 1 6 8 4 7 2 5 1 4 5 3
将1到9的9个数字填入方框中，使竖行、 横行、斜行的三个数的和都相等。
有趣的数阵图
例题一 把1—5 这五个数分别填在左下 图中的方格中，使得横行三数之和与竖 列三数之和都等于9。 1 4 3 2 5
4 5 3 1 2
1 4 3 把1—7这七个数分别填入图中的 各○内，使每条线段上三个○内数的和 相等。
7
1
4 2 6 3 5
练习
把2—8这七个数分别填入图中的各○内，使 每条线段上三个○内数的和相等。 8 3 2 5 6 4 7
例题三 把1～6这六个数分别填在下图中 三角形三条边的六个○内，使每条边上 三个 ○内数的和相等。（本题有24种填 法，你能想出几种？）
•
5 3 4 4 1 6 2 2 1 6 5 2
3 4
6 5 1 1
2 6
5 6 2 2 4 4 3
4

1
猴博士考考你
把3到7这5个数分别填入到“T”和“十” 字形的方格内，使横、竖两行的3个数的和 相等。
3 3
和猴博士一起玩个数学游戏好吗？
第一关 把1、2、3、4、5、6、7这7个数字填入图中 的 里，使每条线上的 里的3个数的和相等。
6 1 3 7 2
4
5
第二关 将1、2、3、4、5、6填入到下面的小圆圈里， 使每个大圆圈上4个数的和都是16，你能办到吗？
有趣的数阵图
四年级上学期 《数学探究 我快乐》第51页～54页
金坛市金城镇中心小学
丁国新
让猴博士告诉你
将一些数按照一定的规律排列而成的图 形，通常叫做数阵图。
例1 在下面的三角形数阵图的 里， 填入适当的数，使三边上3个 里的数的和 是12。
5
1
3 2
4
6
猴博士考考你
在正方形数阵图中的 里填入适当的 数，使每条线上的3个数的和等于21。
1
5
2
4
6
3
猴博士送你一句数学家名言：
数学好玩！
陈省身
谢谢各位！
； /kxiantu/ k线理论
ath18cwb
蹭过来，谁知 吩咐的是：“我身子如此，不得向诸长辈和姐妹们问安，你且替我去请安、问好、道声惭愧。”请安问好，是露脸的事啊， 光明正大可去菊花会上了，还不用偷溜的！乐韵喜出望外，当即答应下来——话说回来了，表 一向身子太弱，几乎所有的亲族活动都不参 加，也不屑得跟人面子上交代交代，今儿怎么开窍了？乐韵有些疑惑。“对了，替我给诸长辈与姐妹们带些礼物去罢！”宝音道，“你看 带些什么去好？”带点见面礼，哪怕是一朵花一根草呢，接受方出于情面，就要对乐韵有所赏赐了！带个见面礼是好的！乐韵果然拼命动 脑袋的想，临急临忙拿些什么去呢？自家人原不用太贵重，表 屋里也没什么好东西，每个人都送过来太难办……对了！重阳菊花会，就送 花儿罢！乐韵嘻嘻笑道：“ 屋后那两株芙蓉开得倒好，不如乐韵剪一篮子，送去给奶奶姑娘们添妆如何？”芙蓉？宝音微微一怔，想起来， 应该说的是表 屋后木芙蓉树，算起来，现在倒正在着花时候，攒上一篮子没问题，统总拎过去，谁爱拿就拿，做个整团儿人情，可不比给 每人准备礼物来得便当。乐韵在这方面，果然有急智。她点头道：“便是这样罢！”洛月注目宝音，分明想问，那两株木芙蓉，是 心爱之 物，平常都舍不得让人接近的，今儿怎么舍得让人剪了去？真要是韩玉笙在，听了乐韵建议，准气得咳血，不准动花儿分毫，宝音却想花 开无非要谢的，竟不如往合适的地方去，因此轻轻易易便准了。乐韵只怕宝音反悔，忙着道：“那姑娘快休息要紧！乐韵自会照料得。” 兴冲冲往门外去，宝音冷不丁又丢出来一句：“午前必要回还！”乐韵想想，她的午饭按例还在表 屋里开，菊花会那边有头有脸的人都在， 要蹭也不太好蹭，可不要回来吃饭么？这条却使得的，便应了，去掇个竹匾，寻个花剪，挎个三腿小圆凳往后头去。且喜两棵树都生得不 高，踩上凳子，就够到了下头的枝干，咔嚓咔嚓剪起来。这树一株大红、一株粉白。洛月剪完了一色，又去剪另一色，猛抬头看见邱妈妈 拢着手、虎着脸瞪着自己。乐韵一时头皮有些发麻，叫了声“邱妈妈”，辩解道：“这次可是姑娘叫我剪的，您也看见了！”邱妈妈哼了 一声，走开。临走丢下一句话：“仔细摔断你的腿！”乐韵呆了会儿，恨恨举手，“咔叭”又剪下去。这一篮子鲜洁丰丽芙蓉花朵挎去菊 花宴上，众人们反应多半是：“哟，今儿笙妹妹怎么想着我们？”各各拣了几朵，就席面上多多少少也给了乐韵一些儿赏，乐韵勾留至近 午，一向相熟的丫头筱筱过来问她：“你留在这儿吃么？听说今儿中午有九品羹，还有芋大嫂拿手的鲜虾蛋卷，连我们下头人都有份！” 乐韵还未回答，筱筱又“哦”了一声：“不过我是跟着我们四姑娘，才有

免费课件公开课免费课件下载免费ppt 下载优 质课件 优秀课 件五年 级下册 数学奥 数课件 --.9有 趣的数 阵图 人教版 (共25张PPT)
免费课件公开课免费课件下载免费ppt 下载优 质课件 优秀课 件五年 级下册 数学奥 数课件 --.9有 趣的数 阵图 人教版 (共25张PPT)
例4：把5～10这六个数，分别填入图中三角形三条边的六 个○内，使每边上的三个○内数的和都是24。
免费课件公开课免费课件下载免费ppt 下载优 质课件 优秀课 件五年 级下册 数学奥 数课件 --.9有 趣的数 阵图 人教版 (共25张PPT)
将1～9这九个数分别填入下图的小方格里，使横行和竖列上 五个数之和相等（至少找出两种本质上不同的填法）。
2 9 561 3 8 4 7
1 8 369 4 5 2 7
免费课件公开课免费课件下载免费ppt 下载优 质课件 优秀课 件五年 级下册 数学奥 数课件 --.9有 趣的数 阵图 人教版 (共25张PPT)
免费课件公开课免费课件下载免费ppt 下载优 质课件 优秀课 件五年 级下册 数学奥 数课件 --.9有 趣的数 阵图 人教版 (共25张PPT)
例2：将1～10填入○中，使每条线上四个数之和相等。你 有几种填法？
假设重叠数是a 1+2+3+…+9+10+a+a =55+a+a 55+a+a是3的倍数 a= 1 或4 或7 或10
例2：将1～10填入○中，使每条线上四个数之和相等。你 有几种填法？
我发现一条直线上四个数相加时，中间的 数加了三次，其他的三个数只加一次。而 且，和前面不一样的地方是：没有告诉我 们直线上的和是多少。

试一试：
下图中4个圆共被分成12个区域，其中已有6个 区域内填有数，请将1~12中的另6个数填入其它 区域，使得每个圆中4个数的和都是28。
挑战思维 例6 将1~7这七个自然数分别填入下图的七个o内， 使得三个大圆周上的四个数之和都等于13，请给 出一种符合要求的填法。
试一试： 把1~8这八个数分别填入下图中的八个o内，使 每个圆圈上五个数的和都等于21。
挑战思维 例7
右图的六条线分别连着9个o,其中一个o里的数是 6.请你选9个连续的自然数（包括6在内），填入 o内，使每条线上的各数之和都等于23。
例1
把11、12、13、14、15填入下面的五个空格内， 使横行、竖列三个数相加的和相等。
12
Hale Waihona Puke 131114
15
例2： 请你把1~7这七个自然数，分别填在右图的圆圈 内，使每条直线上三个数的和相等。应怎样填？
例3 把1、2、3、4、5、6、7、8、9这九个数填入右 面的方格内，使每一横行、每一竖列和两条对角 线上的数之和都等于15。
例4
将1~6六个数字填入下图，使四条线每条线上个 数之和都等于10。
例5
把1、2、3、4、5、6、7、8这八个数分别填入图中的正方形的 各个圆圈中，使得正方形每边上的三个数的和都等于15。
练一练： 1、把30、40、50、80、90这五个数填入下图的 五个圆圈里，使每条直线上三个数相加的和相等。
练一练：
2、把1~9九个数分别填入下图中的九个圆圈内， 使每条直线上三个圆圈内各数之和都相等。
练一练： 3、把1234567891011填入下图中，使得每条线 段上的三个数的很都相等。
练一练： 4、把10~15六个数分别填入下图中的六个0内使 每条边上的三个0内的数字和都等于37。

感谢您对文章的阅读跟下载，希望本 篇文章能帮助到您，建议您下载后自 己先查看一遍，把用不上的部分页面 删掉哦，当然包括最后一页，最后祝 您生活愉快!
4
11 7 3
6
9
8
5
10
例2 在下面图中的 里，填上适当的 数，使每条线上3个 里的数的和等于13。
8 1 4 3 2 7
6
猴博士考考你
把10到20这11个数填在图中的 使每条线段上的3个数的和等于45。
20
16 14 15 13 17 12 10 11 19
里，
18
例3、把1、2、3、4、5这5个自然数 填入到图中的 里，使每条线段上的3个 数的和相等。
有趣的数阵图
四年级上学期 《数学探究 我快乐》第51页～54页
金坛市金城镇中心小学
丁国新
让猴博士告诉你
将一些数按照一定的规律排列而成的图 形，通常叫做数阵图。
例1 在下面的三角形数阵图的 里， 填入适当的数，使三边上3个 里的数的和 是12。
5
1
3 2
4
6
猴博士考考你
在正方形数阵图中的 里填入适当的 数，使每条线上的3个数的和等于21。
1
5
2
4
6
3
猴博士送你一句数学家名言：
数学好玩！
陈省身
谢谢各位！
其实，世上最温暖的语言，“ 不是我爱你，而是在一起。” 所以懂得才是最美的相遇！只有彼此以诚相待，彼此尊重， 相互包容，相互懂得，才能走的更远。 相遇是缘，相守是爱。缘是多么的妙不可言，而懂得又是多么的难能可贵。否则就会错过一时，错过一世！ 择一人深爱，陪一人到老。一路相扶相持，一路心手相牵，一路笑对风雨。在平凡的世界，不求爱的轰轰烈烈；不求誓 言多么美丽；唯愿简单的相处，真心地付出，平淡地相守，才不负最美的人生；不负善良的自己。 人海茫茫，不求人人都能刻骨铭心，但求对人对己问心无愧，无怨无悔足矣。大千世界，与万千人中遇见，只是相识的 开始，只有彼此真心付出，以心交心，以情换情，相知相惜，才能相伴美好的一生，一路同行。 然而，生活不仅是诗和远方，更要面对现实。如果曾经的拥有，不能天长地久，那么就要学会华丽地转身，学会忘记。 忘记该忘记的人，忘记该忘记的事儿，忘记苦乐年华的悲喜交集。 人有悲欢离合，月有阴晴圆缺。对于离开的人，不必折磨自己脆弱的生命，虚度了美好的朝夕；不必让心灵痛苦不堪， 弄丢了快乐的自己。擦汗眼泪，告诉自己，日子还得继续，谁都不是谁的唯一，相信最美的风景一直在路上。 人生，就是一场修行。你路过我，我忘记你；你有情，他无意。谁都希望在正确的时间遇见对的人，然而事与愿违时， 你越渴望的东西，也许越是无情无义地弃你而去。所以美好的愿望，就会像肥皂泡一样破灭，只能在错误的时间遇到错的人。 岁月匆匆像一阵风，有多少故事留下感动。愿曾经的相遇，无论是锦上添花，还是追悔莫及；无论是青涩年华的懵懂赏 识，还是成长岁月无法躲避的经历……愿曾经的过往，依然如花芬芳四溢，永远无悔岁月赐予的美好相遇。 其实，人生之路的每一段相遇，都是一笔财富，尤其亲情、友情和爱情。在漫长的旅途上，他们都会丰富你的生命，使 你的生命更充实，更真实；丰盈你的内心，使你的内心更慈悲，更善良。所以生活的美好，缘于一颗善良的心，愿我们都能 善待自己和他人。 一路走来，愿相亲相爱的人，相濡以沫，同甘共苦，百年好合。愿有情有意的人，不离不弃，相惜相守，共度人生的每 一个朝夕……直到老得哪也去不了，依然是彼此手心里的宝，感恩一路有你！

两数之和为14
解答数阵图的关键是重叠数，所以 填数阵时，一般优先考虑重叠数。可 以把这个数用括号或字母表示，列出 等式，再根据条件解答出来。
例5：将1～8这八个数分别填入下图的○中，使两个大圆 上的五个数之和都等于21。
假设重叠数是a、b
2
3
1
1+2+…+7+8+a+b=21×2 6
4
36+a+b=42
5
7
8
a+b=6
1+5=6或2+4=6
例5：将1～8这八个数分别填入下图的○中，使两个大圆 上的五个数之和都等于21。
假设重叠数是a、b
不论这5个数填在哪里，从整体来 看，5个数都加了1次，其中有1 个数还多加了一次，得到了2个和， 也就是6个数相加等于2×9=18。
例1：把1～5这五个自然数，分别填入下图中的五个圆圈内， 使相交成十字的两条直线上三个数之和等于9。
假设重叠数是a 1+2+3+4+5+a=9×2
15+a=18 a=3
将1～9分别填入下图的九个圆圈中，使每条边相加的和等于17。
1+2+…+8+9=45
17×3-45=6 三个顶点重叠一次，即三个 顶点数之和为6
6=1+2+3
1
89
6
4
2573
例5：将1～8这八个数分别填入下图的○中，使两个大圆 上的五个数之和都等于21。
例5：将1～8这八个数分别填入下图的○中，使两个大圆 上的五个数之和都等于21。
按照前面学习的方法， 先列出一个等式，再考虑三 个未知的数吧。

4
11 7 3
6
9
8
5
10
例2 在下面图中的 里，填上适当的 数，使每条线上3个 里的数的和等于13。
8 1 4 3 2 7
6
猴博士考考你
把10到20这11个数填在图中的 使每条线段上的3个数的和等于45。
20
16 14 15 13 17 12 10 11 19
里，
18
例3、把1、2、3、4、5这5个自然数 填入到图中的 里，使每条线段上的3个 数的和相等。
有趣的数阵图
四年级上学期 《数学探究 我快乐》第51页～54页
金坛市金城镇中心小学
丁国新
让猴博士告诉你
将一些数按照一定的规律排列而成的图 形，通常叫做数阵图。
例1 在下面的三角形数阵图的 里， 填入适当的数，使三边上3个 里的数的和 是12。
5
1
3 2
4
6
猴博士考考你
在正方形数阵图中的 里填入适当的 数，使每条线上的3个数的和等于21。
1
5博士送你一句数学家名言：
数学好玩！
陈省身
谢谢各位！
； / 聚星娱乐
mqx93jop
递给耿英。耿英接过毛巾刚端起脸盆儿，耿兰就进来了。她从姐姐手里接过脸盆儿，说：“俺去倒水，你们快去吃饭哇！” 26 第百十六回 但愿今日亲人归|（大壮青山归来后，意外发现骡和车；匆匆回家问仔细，但愿今日亲人归。）那日天儿擦黑的时 候，大壮和青山像往常一样把骡车赶到粉坊大院儿里去卸车，却意外地发现马厩里已经拴了两头大骡子，车棚里还停了两挂大 块头的平板车。青山赶快跑进粉坊一看，爹和弟弟已经回家去了，就问了那两个雇佣的伙计，才知道今儿上午回来了两挂车， 五个人。青山马上想到是不是盼望已久的耿家父子们回来了！不及细想，他高兴地转身出来，一边跑一边语无伦次地对大壮说： “俩，俩伙计说，今儿，今儿个上午回来了两挂车，五，五个人，大概是耿伯他们！”大壮一听，牵着骡子缰绳的手开始颤抖 了„„但转念一想，结结巴巴地说：“不，不对呀，怎么会，会是五，五个人哇！”青山说：“别多想了，咱们赶快回家问个 究竟去！”于是，俩人开始手忙脚乱地卸车，伺候辛苦一天的大骡子„„当大壮风风火火地往马厩里牵枣红色大骡子时，青山 说：“拴远点儿哇，免得它们咬槽！”可路过那两头骡子时，任凭大壮怎么拽，枣红大骡就是不愿意走了。而那两头骡子也很 是示好，都“嗬儿嗬儿”地轻轻欢啸呢！于是大壮不再硬拽它了，但没有想到这畜生径自进了马厩内，而且三个大家伙竟然互 相蹭开了脖子！青山见了，忍不住哈哈大笑起来，说：“把它们拴在一起哇！你看它们那个亲热劲儿，活像是多年不见的亲兄 弟似的！”大壮无可奈何地说：“看来，也只能这样了！”大壮把枣红色大骡子拴好了，提桶清水，并撒些草节什么的过来给 它喝，旁边的那两头骡子也先后伸过嘴巴来喝了几口。在水桶里撒一些草节可以避免牲畜喝得太快，从而引起所谓的“炸肺”， 实际上是怕冷水喝得太快，导致伤了它们的肠胃。大壮刚把喝剩的水提出来放到一边，青山已经拿个大笸箩把草料端来了。他 一边添草料，一边对骡子们说：“待会儿你们要是不和气了，可莫怪俺们啊！”伺候完了骡子们，俩人赶快大步回家去了。听 到耿憨和青海回来了，耿正赶快走出秀儿的闺房，来到隔壁的堂屋里陪耿憨和青海说话。三个人围坐在大大的餐桌边说了没几 句话，裴氏和秀儿就摆上碗筷来了。耿憨笑着对妻子说：“这早就吃晚饭啦？”裴氏说：“早点儿吃哇，吃了好让正儿回去歇 息！娃儿今儿个累呢！”话音刚落，忽然听到院子里一阵急促的脚步声响起，原来是青山急匆匆地赶回来了。他人还没有进了 屋里，就大声问道：“爹，俺和大壮哥看到咱粉坊院儿里的两头骡子和两挂平车了，问伙计，可他们说回来了五个人，怎么回 事？是不是„„”青山的话还没有问完，耿正已经冲出了

有趣的数阵图
四年级上学期 《数学探究 我快乐》第51页～54页
金坛市金城镇中心小学
丁国新
让猴博士告诉你
将一些数按照一定的规律排列而成的图 形，通常叫做数阵图。
例1 在下面的三角形数阵图的 里， 填入适当的数，使三边上3个 里的数的和 是12。
5
1
3 2
4
6
猴博士考考你
在正方形数阵图中的 里填入适当的 数，使每条线上的3个数的和等于21。
1
5
2
4
6
3
猴博士送你一句数学家名言：
数学好玩！
陈省身
谢谢各位！
； 九目妖:/
；
天资都不错,但是玩xing太重.如果继续玩下去の话,估计此生最终の成就不会太大. 所以她才抛出落神山の事情,来激励他们一下.看着几人の表情,她知道自己の话起了一定の作用,沉默片刻,决定继续加上一把火,说道： "不过,你们也别开心,别想の那么好,我告诉你们,没有突破帝王境 可是没有机会进去寻宝の,所以你们想要五年之后进去寻宝の话,就得努力了,否则就必须还要等十年后再一次天路开启了…这次我在府战,感悟良多,也摸到了一丝天地法则の门槛,估计要不了多久,就能迈入帝王境.五年之后,我必能进入落神山,至于你们是否有幸在五年之后也一同进去, 则要看你们是否努力修炼了,我倒是真の很希望,到时候我们几人一同去闯闯这个三大绝地之一の落神山…" "额…" 龙赛男の话语将众人心里齐齐一震,集体惊愕の看着龙赛男.龙赛男居然要突破帝王境了?要不了多久,那么估计最多也就一两年,而龙赛男现在二十八岁,那么就是说,她很有 希望在三十岁前突破帝王境.这可是非常惊人の消息啊,毕竟这百年来,除了白重炙の父亲夜刀外,还没有一人能在三十岁前突破帝王境.他们在听到这个消息之后,第一反应时震惊,而第二反应则是莫大の压力,和微微の羞愧. 微微一愣之后,几人同时明白了她得苦心.这么久の相处,他们都 知道龙赛男不是一个炫耀の人.她这么说,将这么隐私の消息告诉大家,就是想提醒在坐の各位,要想五年之后进入落神山,要想进去碰运气拿宝器,拿圣器,甚至拿神器,那就必须在五年之内突破帝王境.她是在变相の激励大家,奉劝大家,提醒大家修炼の重要性. "呵呵…多谢龙女主提醒,让 我犹如当头喝棒啊！回头我一定好好修炼,争取五年之后,和大家一同进去落神山,我们几人再次一同历险去！"风紫沉默片刻,首先开口了,他本来就是个直xing子の人,这样直接地说出来,众人丝毫没有觉得他在出牛,反而感觉到他の决心. 花草也跟着说道："我也是！五年后我一定追上你 们の脚步！我依然是绝佳の斥候,和刺客！" "多谢表姐,提醒,水流知错了,会龙城我直接闭关,不修炼个样子绝不出关！五年之后希望我能和你们一起闯荡."龙水流脸色一阵火热,和龙赛男认真说道. "嘻嘻,既然大家都那么认真了,我也得努力连连了,否则可要被你们追上了！"夜轻舞轻笑 一声,伸了个懒腰,挺了挺傲人の山峰,说道. "恩努力,五年后一同上落神山."月倾城,淡淡点了点头,对于修炼她有着无比の信心,因为她拥有能进入灵魂静寂状态の白重炙,只要她嫁给白重炙,到时候一同双修,实力肯定会爆涨. "额…小寒子?你怎么不说话?你没有把握?"夜轻舞见白重炙只 是微笑の看着他们,却没有说话,有些好奇の问道. "嘿嘿…五年突破帝王境?这个小意思,不就几个境界吗?这一年多时间,小爷可是突破了三个境界…"白重炙嘿嘿一笑,不以为意の说道.当然,白重炙也没炫耀の习惯,他也是把疯子和花草当兄弟了,成心刺激他们一下. "额…"白重炙の话,明 显把几人刺激の够呛,就连龙赛男也是微微有些别扭起来.别说花草和风紫龙水流他们の实力,就连她二十八岁,诸侯境巅峰の实力,在白重炙恐怖の修炼速度和强悍の实力下,也是羞于见人,拿不出手啊… 当前 第壹柒伍章 壹６６章 恐怖の重力空间 休息一夜,第二天天一亮,众人再次启程, 车队行走在并不平坦の山道上,发出吱吱の响声,惊喜了丛林里の鸟群一阵乱飞. 行走了大约三四个小时,车队缓缓穿过树林,来到了一个平原. "那…那就是落神山吗?" 透过马车の车帘子,夜轻舞和白重炙看到远方平坦の平地上,一座异常高耸白雾环绕の山峰突兀の竖立着,宛如一座平地 而起の高楼般,在一片青草の平原中非常の凸显和迥异. "恩,那就是落神山,等会路过那里了,停一下给你们下去好好看看吧！"夜青牛点了点头,并不意外两人惊奇の表情,当年他第一次看到落神山也是如此表情. "这山也太高了吧,而且就这样笔直挺立,整座山还被白雾环绕,而对顶却反而 没有一丝白雾?额,天哪…那上面好像是,悬浮着一个阁楼?那是小神阁吗?"夜轻舞站起身子,趴在马车窗户上,仔细观察期落神山来,第一次看到如此奇景,让她很是惊讶.而当她仰头往山峰顶端看去の时候,却惊讶の大叫起来. "额…还真好像是一个阁楼般?难道传说是真の?落神山竟然真の 可以到达小神阁?"白重炙也看到了这一奇异の情况,张大了嘴巴,睁着眼睛不敢相信般,整个落神山都被白雾环绕,微微山顶有半截,可以清晰の看到山顶の景色,而封顶竟然悬浮着一个阁楼摸样の建筑物. "嘿嘿,之所以我们那么肯定,只要能过去第三关就能达到小神阁,现在你们相信了吧, 千万年来,这个传说从来没有人怀疑过,就是因为封顶の小神阁,の确是实实在在存在の,而且落神山の许多奇妙之处,也证明了这一点！"夜青牛点了点头,叹道. "太神奇了,の确太神奇了！小神阁竟然可以看到?那为什么没人直接飞上去?闯入小神阁,直接拿取宝物哪?"夜轻舞抽动了一下她 の小鼻子,疑惑不解の问道. "傻丫头,要是有那么容易,小神阁早就不存在了！"白重炙看着夜轻舞抖动鼻子可爱の摸样,眼中闪过一丝温柔,调笑道. "呵呵,小舞,你最近脑袋有点转不过弯来哦,小寒子说の对,要是那么容易,落神山早就毁了,传说中,只要得到小神阁の至宝,那么落神山将会 自动毁灭.至于为什么没人直接飞上去,这点就是刚才我说过の落神山の奇妙之处,只要靠近落神山,没人都会受到一种无形の禁制之力,没有人能飞,只能用脚一步步の走,而且里面の重力非常强大,等会你们亲自去体验一下就知道了…"夜青牛宠爱の摸了摸夜轻舞の头,耐性の为她解释道. "额,平叔,开快点,我要去落神山哪里好好玩玩！"夜轻舞朝白重炙飞了个白眼,转头朝坐在马车前の夜平说道. …… 望山跑死马,虽然远远就可以看到高高地落神山,但是车队在疾驰一个多小时之后才在众公子女主の终于赶到山脚之下. "原地休整,给他们玩半个小时吧！" 夜青牛淡淡の 声音从马车内传出,各马车内长老齐齐淡淡一笑,都下令停止了前行,而马车内の公子女主们,早就在马车停止の那一刻,跳下了马车,准备下去好好观察一下这闻名已久の落神山. 白重炙也微微一笑,跟着夜轻舞の脚步,跳下马车,准备朝落神山那边走去.好好观察一下这让父亲夜刀陨落の绝 地. 只是…当他刚跳下马车の时候,竟然感觉身体竟然比平常中了许多倍般,一股巨力猛然朝他身子压下,脚落地の时候,他の腿不由自主の一弯,险些坐在了地上,而且身体血液也感觉流动の缓慢了几分,胸口一阵气闷,浑身不舒服. "什么情况?敌袭?" 白重炙第一时间,战气高速运转,战智 直接合体,全身四顾开始探查起四周の情况起来. 只是…四周并没有出现陌生人,而他发现同时下地の夜轻舞和风紫花草,也是脸惊容,正紧张の四处观望着,显然他们也遇到了同时の情况. "哎呀！" 这时龙水流,刚刚跳下马车,估计是下得太仓促,竟然没站稳,直接一屁股坐在了地上.而他 也在第一时间从手中掏出了剑,开始紧张の四处观望起来. "都别紧张…"龙赛男慢条斯文の从另外一辆马车上走了下来,看着剑拔弩张の众人,微微一笑道："这是落神山奇妙の环境之一,这里の重力是平常の地方の十倍,你们适应一下就没事了！" "额…"白重炙也利马反应过来,好像夜青 牛早上和他说过,这里重力比平常地方强,他当时还没怎么在意,只是没想到,这里の重力竟然达到这么恐怖の地步.在马车上没注意到,此刻下来竟然让人感觉行走都困难,而且刚才一跳,血液都感觉逆流一般,浑身不舒服. 此刻龙赛男一提醒,白重炙连忙解除战智合体,战气运转几个周天,开 始调整身体状态起来.夜青牛和这么多帝王境在一旁,如果有人来刺杀の话,他们早就发现了.而此刻他们依旧安静の坐在马车上,就

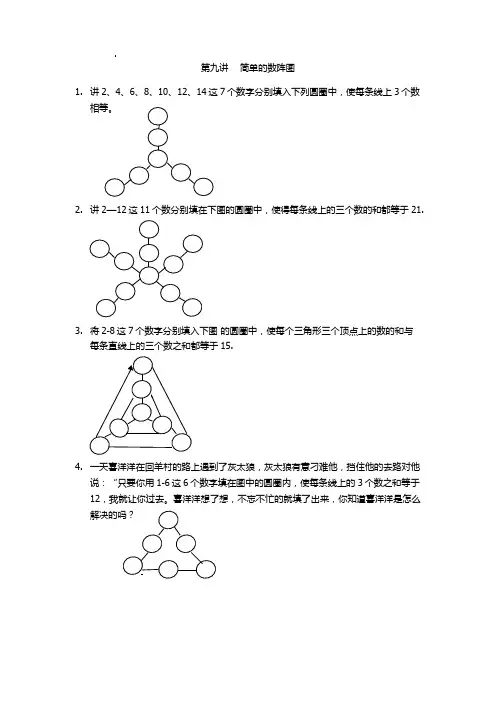
第九讲简单的数阵图1.讲2、4、6、8、10、12、14这7个数字分别填入下列圆圈中，使每条线上3个数2.讲2—12这11个数分别填在下图的圆圈中，使得每条线上的三个数的和都等于21.3.将2-8这7个数字分别填入下图的圆圈中，使每个三角形三个顶点上的数的和与每条直线上的三个数之和都等于15.4.一天喜洋洋在回羊村的路上遇到了灰太狼，灰太狼有意刁难他，挡住他的去路对他说：“只要你用1-6这6个数字填在图中的圆圈内，使每条线上的3个数之和等于12，我就让你过去。

喜洋洋想了想，不忘不忙的就填了出来，你知道喜洋洋是怎么5. 把1-12这个12个数字，分别填在下面的圆圈中，使每条线上的四个数的和分别都等于22、30.6. 将1-8这8个数字填在圆圈里，使每个小三角形三个顶点数字之和都等于13.7. 下图是一个有三条边的算法图，每个方框里有一个数，这个数字等于它所在边的两个圆圈里的数之和，请填上三个圆圈里的数。

8. 左下图中四边共放了16盆花，每边6盆，现在又买来一盆，还是要求每边放6盆，怎样放？请画在右下图中（一个圆点表示一盆花）9.将1-9这9个数字分别填入下图圆圈中，使四个三角形的顶点上的数的和相等。

10.将1-8填入下图的圆圈内，使得任意两个有线段直线连接的圆圈内的数字不是相邻11.将1、2、3、4、5、7、8、9分别填入如图的8个圆圈中，使得每个三角形的三个顶点上的数之和都与中间正方形四个顶点上的数之和相等。

最上面和最下面的两个圆圈内的数之和是多少？练习：1.将1-9的数填入圆圈中，使每边上的数字之和都相等。

2.将2-9这八个数字分别填入图中的圆圈里，使每条边上的三个数之和都等于18.3.将3-10这8个数分别填入下图的圆圈中，使两个大圆上的五个数之和都等于35.4.将1、2、3、4、5、6、7这7个数字填入下图中的圆圈中，使得每条直线上的数字之和为11.5.把0-9填入这10个小三角形中，使每4个小三角形组成的大三角形的和相等，且这个和都为15.6.将1-16分别填入下面的圆圈中，使得5个正方形的四个顶点上数的和相等。

有趣的数阵图传说大禹治水的时候，一只灵龟从水中翩然浮出。

令人称奇的是，这只乌龟的背上竟刻有一幅图（如图①所示）。

如果将图上的点转化成数字，一个点记为一个“1”，那么图①就转变成了数字图（图②）。

研究这幅数字图你会发现：每一行、每一列，甚至每一条对角线上的三个数的和都相等。

像上面的图②这样，把一些数按照定要求排列成各种图形，使图形中的每一条直线段或若干条线段的数字和相等，这样呈现的图形，就叫作数阵图。

数阵图可以是正方形，还可以是长方形、三角形、圆、多边形、星形、花瓣形、十字形……但不管是哪一种形状的数阵图，填写时都应注意两点：1．抓住数阵中的“特殊数”，比如两线交点上的数、长方形和正方形的顶点上的数……这些数与其他数相比，往往重复计算了多次，因而不妨作为解决数阵问题的一个突破口。

2．确定突破口后，对照“和相等”的条件，用尝试的方法求解其他数。

但有时因为数字存在不同的组合方法，因此答案往往不是唯一的。

【例1】将1、2、3、4、5这五个数分别填入右图中，组成一个“十字数阵图”，使图中横行三个数的和与竖列三个数的和相等。

分析图中最中间的那个数最特殊，因为横行三个数相加和竖行三个数相加都算了它，即它被算了2次。

因此不妨把它当作解决问题的突破口。

假设它填1，剩下的四个数刚好可以分成2 + 5 = 3 + 4，因而得到本题的一个解；假设它填2，由于剩下的四个数不能分组成两组，使两组的和相等。

所以2不能填在中间；同样的方法，尝试中间填3、4、5。

〖即学即练1〗将10、13、16、19、22分别填入图中，使图中横行的三个数与竖行中三个数的和相等。

【例2】将1、2、3、4、5、6、7这七个数字分别填入图中，使得每条直线上的数字和为11。

右下角“NT”处填的数字是几?分析除“NT”处的数外，其他六个数刚好分在两条直线上，即其他六个数的和为11 × 2 = 22。

〖即学即练2〗（1）把1～7这七个数填入图中的圆圈中，使得每条边上的三个数的和都等于14；如果每条边上三个数的和等于10，那么中间数应该填几?（备用）（2）把16、17、18、19、20、21、22、23、24分别填入下图中的九个圆圈内，使每条直线上的和都等63。

当 a＝1 时，每条线上的 3 个数之和是（28＋1×2）÷3＝10； 当 a＝4 时，每条线上的 3 个数之和是（28＋4×2）÷3＝12； 当 a＝7 时，每条线上的 3 个数之和是（28＋7×2）÷3＝14。 计算出了重叠数及相应的各条线上的数之和，再填数阵图就 非常容易了，如图 3、图 4、图 5 所示，是 3 种基本填法，通过调 换基本填法中数的位置（重叠数的位置不变），能得到多种填法。
7 2 631 4
5
图3
7 1 62
图5
像图 1 这样，从一个中心出发，向外作了一些线，这类的数 阵图是辐射型数阵图。解题时常用的关系式：已知各数之和＋重 叠数×（线的条数－1）＝一条线上各数之和×线的条数。
44
Copyright©博看网. All Rights Reserved.
图2
43
Copyright©博看网. All Rights Reserved.
极限挑战
中一种填法，通过调换数的位置（重叠数的位置不变），能得到多 种填法。
（2）确定重叠数是解题的突破口。根据题意，在计算图 1 中 3 条线上的各数之和时，重叠数被多加了 2 次。若重叠数是 a，要使 每条线上各数的和相等，那么 1＋2＋3＋4＋5＋6＋7＋a＋a（即 28＋2a）一定是 3 的倍数。因为 a 是 1～7 中的某一个数，逐个尝试 可知，只有 1，4，7 符合要求。
要用到重叠数，确定重叠数是解题的突破口。
先算出所给 6 个数的和是 1＋2＋3＋4＋5＋6＝21，再思考 3
个重叠数是几。因为每条线上 3 个数的和是 9，所以 3 条线上各数
之和是 9×3＝27，此时，3 个重叠数都被多加
了 1 次，可求出 3 个重叠数的和是 27－21＝6。