大数的认识主题单元设计及思维导图

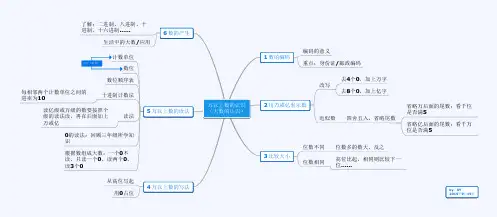
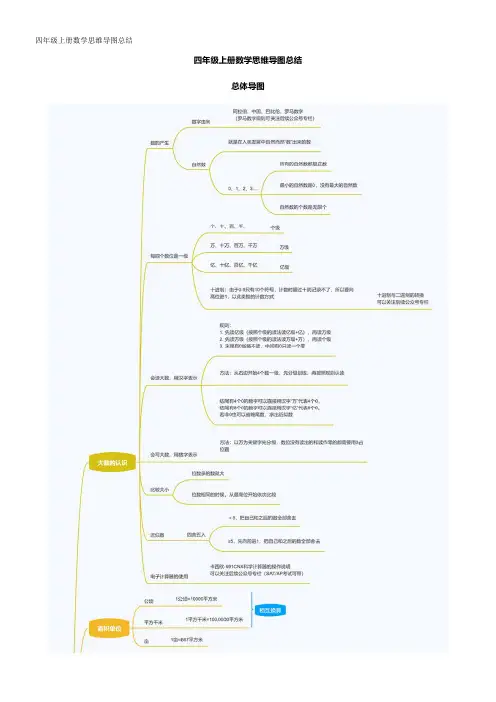
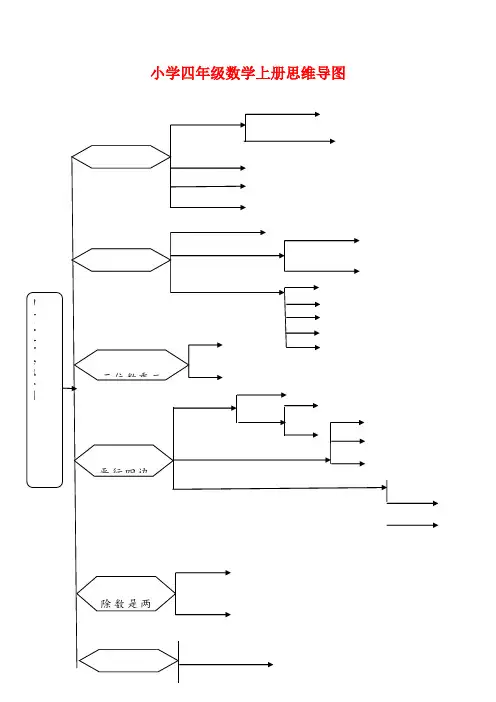
四年级上册数学思维导图总结总体导图第1单元知识点1.大数的认识1、计数单位：一（个）、十、百、千、万……亿等等，都是计数单位。

相邻两个计数单位之间的进率是十。

2、数位：个位、十位、百位、……亿位等等，都是数位。

数位名称就是在相应的计数单位后添一个“位”字，如：万--万位。

3、数级：个级、万级、亿级……都是数级，一个数级包括四个数位。

4、数位顺序表：含有数级、数位和相应的计数单位的表格叫做数位顺序表，如下。

5、数字表示：某个数位上的数字表示几个这个数位的计数单位。

如：12367 中的2在千位上，表示“2个千”某个数级上的数字表示几个这个数级的计数单位。

如：36472845中的3647在万级上，表示“3647个万”6、大数的读法：①从高位数读起，一级一级往下读。

②万级的数要按照个级的数的读法来读，再在后面加一个万字。

③每级末尾不管有几个零都不读，其他数位有一个“零”或连续几个“零”，都只读一个“零”。

读数注意事项：“2”读作“二”；如果是大数的最高位是十位、十万位、十亿位……且最高位上的数字是“1”时，这个“1”不读，如125046读作“十二万五千零四十六”7、读写数检验方法：读数和写数可以互相检验，即读数后再写出来和原数比对，而写数后可以自己读出。

②当这两个数位数相同的时候，我们就应该从左起的第一位比起，也就是从最高位开始比，哪个数最高位上的数大，这个数就大。

③如果碰到最高位上的数相同的时候，就再比下一位，以此类推，直到我们比较出相同的数位上的那个数，哪个数大的时候，我们就可以断定这个数比较大。

8、四舍五入法：求“近似数”的一种方法，首先确定需要精确到的数位，将其后面的数作为“尾数”，对尾数最高位上的数字进行取舍。

0~4为“舍”，尾数清零且精确数位的数字不变，5~9为“入”，尾数清零且精确数位上的数字加1。

如：12,5933 （精确到万位）≈13,000012,5933 （精确到千位）≈12,600012,5933 （精确到百位）≈12,590012,5933 （精确到十位）≈12,5930注意：四舍五入后的结果是近似数，所以符号一定要用“≈”！9、改写成不同计数单位的数：（1）整万数：将个级的4个0改写成“万”，整亿数：将万级、个级共8个0改写成“亿”如，15,0000 = 15万24,0000,0000 = 24,0000万= 24亿370,0000 = 370万注意：整万、整亿的数的改写属于准确数，要用“=”连接！（2）非整万的数改写成以“万”为单位的数：将万位以后的数作为尾数，对尾数的最高位（千位）四舍五入，再改写成以“万”为单位的数如14,7283 ，因为千位上的数字是7，属于“入”的情况，所以14,7283 ≈ 15,0000 = 15万或者直接写成14,7283 ≈ 15万（3）非整亿的数改写成以“亿”为单位的数：将亿位以后的数作为尾数，对尾数的最高位（千万位）四舍五入，再改写成以“亿”为单位的数如56,0384,9182 ，因为千万位上的数字是0，属于“舍”的情况，所以56,0384,9182 ≈ 56,0000,0000= 56 亿或者直接写成56,0384,9182≈ 56亿10、按要求组数：（1）组成最大、最小的数：“用2、4、5、6、0、9组成最大的六位数和最小的六位数”最大的数：把给定的数字按照从大到小的顺序排列即可，得965420最小的数：把给定的数字按照从小到大的顺序排列即可，若最高位上的数字是0，将第一个非0数字提前作为最高位，得024569 –》204569（2）组成特定读法的数：“用2、4、5、0、0组成读出1个0的数”按照读数规则，先把0的位置确定，只读1个0，则这个0不能在每级末尾，又已知这个数是五位数，所以单个0可以出现的数位有十位、百位、千位，连续两个0可以出现的位置有千位和百位、百位和十位。

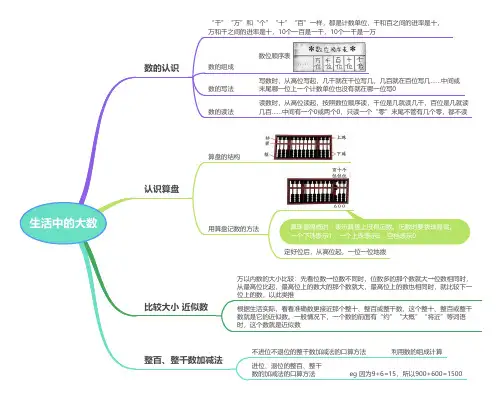
四年级上册《大数的认识》主题单元设计及思维导图
第二课时数的大小比较
一、复习。

在〇里填上“›”、“‹”或“＝”，并说说比较的方法。

985〇1020 504〇725 687〇678
二、探究活动。

1.出示我国部分省份的土地面积，请学生选择任意两个省的面积进行大小比较，用自己的话说说比较两个数大小的方法。

2.尝试排列大小：读出下面各数，并按从小到大的顺序排列。

5100360 10213800 5001370 680590
3.交流学习体会。

通过以上探究，你有哪些收获？还有哪些疑惑？
三、巩固练习
1.完成“做一做”。

2.比较下面每组中两数的大小。

93604和903604 370300和307300
四、课堂总结：通过今天的学习，你有什么收获？
第三课时多位数的改写与省略
. Word 文档。

大数的认识思维导大数，指的是比常规数值大得多的数。

在数学中，大数通常是指超出某个特定范围的数，例如超过可表示的最大整数或最大浮点数。

大数的认识需要一种特殊的思维导向，因为它们超越了我们常规的数学概念和直觉。

大数的概念需要我们放弃对数字大小的直觉。

我们习惯于处理小规模的数值，而大数往往远远超出我们的想象。

例如，我们可以轻松理解1加1等于2，但当涉及到超大数时，我们可能无法想象1加上一个无穷大的数会是什么结果。

大数的认识需要我们从常规思维中解放出来，接受数学中更为抽象和复杂的概念。

大数的计算和表示需要特殊的方法和工具。

常规的计算机和计算器往往无法处理大数运算，因为它们的位数和精度有限。

为了处理大数，我们需要使用特殊的算法和数据结构，如大数运算库或高精度计算器。

这些工具可以处理任意位数的数值，从而使我们能够进行复杂的大数计算。

大数在实际应用中具有重要的作用。

在密码学中，大数被广泛用于加密和解密算法中。

由于大数的复杂性和难以破解性，它们被用于保护敏感信息的安全性。

在科学研究中，大数也常常出现在计算模拟和数据分析中。

例如，模拟宇宙的演化过程需要处理大量的粒子和复杂的物理规律，这就需要使用大数来表示和计算。

大数还涉及到概率和统计的概念。

在概率论中，大数定律指出，当样本容量足够大时，样本平均值将趋向于总体平均值。

这个定律揭示了大数的规律性和稳定性，为我们理解和预测复杂系统的行为提供了依据。

大数的认识需要我们具备一种开放和探索的心态。

大数世界充满了未知和挑战，但也蕴藏着无限的可能性。

我们需要不断学习和探索，以不断拓展我们对大数的认知和理解。

大数的认识需要一种特殊的思维导向，并涉及到特殊的计算方法和工具。

大数在实际应用中具有重要的作用，并与概率统计和科学研究密切相关。

了解和理解大数的概念和特点，对于我们拓展数学思维和解决复杂问题具有重要意义。

四年级上册数学思维导图1~8单元1.大数的认识1、计数单位：一（个）、十、百、千、万……亿等等，都是计数单位。

相邻两个计数单位之间的进率是十。

2、数位：个位、十位、百位、……亿位等等，都是数位。

数位名称就是在相应的计数单位后添一个“位”字，如：万--万位。

3、数级：个级、万级、亿级……都是数级，一个数级包括四个数位。

4、数位顺序表：含有数级、数位和相应的计数单位的表格叫做数位顺序表，如下。

5、数字表示：某个数位上的数字表示几个这个数位的计数单位。

如：12367 中的2在千位上，表示“2个千”某个数级上的数字表示几个这个数级的计数单位。

如：36472845中的3647在万级上，表示“3647个万”6、大数的读法：①从高位数读起，一级一级往下读。

②万级的数要按照个级的数的读法来读，再在后面加一个万字。

③每级末尾不管有几个零都不读，其他数位有一个“零”或连续几个“零”，都只读一个“零”。

读数注意事项：“2”读作“二”；如果是大数的最高位是十位、十万位、十亿位……且最高位上的数字是“1”时，这个“1”不读，如125046读作“十二万五千零四十六”7、读写数检验方法：读数和写数可以互相检验，即读数后再写出来和原数比对，而写数后可以自己读出。

②当这两个数位数相同的时候，我们就应该从左起的第一位比起，也就是从最高位开始比，哪个数最高位上的数大，这个数就大。

③如果碰到最高位上的数相同的时候，就再比下一位，以此类推，直到我们比较出相同的数位上的那个数，哪个数大的时候，我们就可以断定这个数比较大。

8、四舍五入法：求“近似数”的一种方法，首先确定需要精确到的数位，将其后面的数作为“尾数”，对尾数最高位上的数字进行取舍。

0~4为“舍”，尾数清零且精确数位的数字不变，5~9为“入”，尾数清零且精确数位上的数字加1。

如：12,5933（精确到万位）≈13,000012,5933（精确到千位）≈12,600012,5933（精确到百位）≈12,590012,5933（精确到十位）≈12,5930注意：四舍五入后的结果是近似数，所以符号一定要用“≈”！9、改写成不同计数单位的数：（1）整万数：将个级的4个0改写成“万”，整亿数：将万级、个级共8个0改写成“亿”如，15,0000 = 15万24,0000,0000 = 24,0000万= 24亿370,0000 = 370万注意：整万、整亿的数的改写属于准确数，要用“=”连接！（2）非整万的数改写成以“万”为单位的数：将万位以后的数作为尾数，对尾数的最高位（千位）四舍五入，再改写成以“万”为单位的数如14,7283 ，因为千位上的数字是7，属于“入”的情况，所以14,7283 ≈ 15,0000 = 15万或者直接写成14,7283 ≈ 15万（3）非整亿的数改写成以“亿”为单位的数：将亿位以后的数作为尾数，对尾数的最高位（千万位）四舍五入，再改写成以“亿”为单位的数如56,0384,9182 ，因为千万位上的数字是0，属于“舍”的情况，所以56,0384,9182 ≈ 56,0000,0000=56 亿或者直接写成56,0384,9182≈ 56亿10、按要求组数：（1）组成最大、最小的数：“用2、4、5、6、0、9组成最大的六位数和最小的六位数”最大的数：把给定的数字按照从大到小的顺序排列即可，得965420最小的数：把给定的数字按照从小到大的顺序排列即可，若最高位上的数字是0，将第一个非0数字提前作为最高位，得024569 –》204569（2）组成特定读法的数：“用2、4、5、0、0组成读出1个0的数”按照读数规则，先把0的位置确定，只读1个0，则这个0不能在每级末尾，又已知这个数是五位数，所以单个0可以出现的数位有十位、百位、千位，连续两个0可以出现的位置有千位和百位、百位和十位。

四年级上册《大数的认识》主题单元设计及思维导图
数学
外语
历史
社区服务
2.教师出示计算器，任意拨数，学生读出计数器上的数，并写下来。

二、探究万以上数的读写
1.提出问题：我们身边有哪些比“万”还大的数呢？学生展示课前从网络资源上查找到的资料。

2.全班交流探讨：比“万”更大的数，还有多少新的计数单位？每相邻两个计数单位之间是什么关系？你是怎么想的？
3.出示数位顺序表，小组合作：怎样读写万以上的数。

三、交流汇报
1.小组汇报读数、写数的方法。

2.教师提问：每一级的中间或末尾有0时怎么办呢？
3.利用刚才总结的方法读出自己小组课始收集的数据
四、巩固练习
1.练习一中的第6－9题，直接填在教科书上。

2.写出下面各数。

（课件出示）
（1）有三个百万，九个千和五个十组成的数是（）。

（2）一个六位数，最高位上是8，最低位上是5，其余各位上都是0，这个数是（）。

（3）50个千万组成的数是（）。

（4）由三个0，三个6，三个8组成的最大的九位数是（）。

（5）与499999999相邻的两个自然数是（）。

五、全课总结：今天你有什么收获？还有什么问题？
六、板书设计：
大数的读写。

大数的认识思维导图大数的认识，是四年级第一学期的教学内容，共分约12课时的教学任务，继接三年所学大数的知识为基础，以计数器为学具，以计数器为拓展的大数的初步学习，进一步认识更大的数的读写及生活中的运用，并能在数据的收集整理过程中，认识近似数。

大数的认识思维导图把学习内容主要有四个部分：亿以内数的认识、亿以内数的读写、大数的改写及近似数的认识.教学重点是对“亿以内的数”的准确读数或写书，难点是“亿以内的数”中“0”的读与不读,写与不写。

在教学过程中，通过大数的认识思维导图创设情境，让学生感受大数的存在.首先通过让学生自由汇报收集到的信息，及结合教材提供的素材,创设具体的情境,让学生充分感受到大数的存在，进一步扩充了学生对“数”的认识。

并且相信学生,让学生自主探究。

在教学数位、数级、计数单位、十进关系、数的组成等知识时,采取让学生自学并发现其中的规律。

学生由于已经有万以内数的认识的基础，所以对于数位、十进关系和数的组成的相关知识很快就掌握了。

对于“数级”和“计数单位”这两个新的知识点,学生通过自学也很快理解了。

在此环节的教学，教师只起到了一个帮助学生梳理新知的角色及向学生介绍国际上的“三位分级法". 教学中充分应用计数器的规律性，让学生快速准确记忆计数器从右向左的依次数位，通过拍手游戏、闭眼空间形象记忆法,使学生掌握相邻两个数位之间的进率都是“十”的结论。

同时牢牢把握亿以内数“四个一分级，读几就写几，缺位用零补,读数从高向低位”.“四舍五入"更好掌握，题目规定近似那个位,采取“四舍五入”法，看此数位满“5”进位，不足“5"时,后面的数位全部近似为“0”计数时，带单位可省去该数位后面的“0”，再写上单位。

利用大数的认识思维导图采取四个分层来授课:一是在备课中分层，从知识的疑难程度由浅入深、由易到难有层次、有梯度设计教学、设计课堂;二是在讲课中分层，让简单更容易掌握的知识点竟可能使每个学生都掌握，知识的演变和综合应用部分能使大多数学生基本掌握,了解知识的贯穿途径,在拓展和探究发展的内容当中，可在用时少，题目精炼,鼓励少数发展中或有能力的学生去思考、去学习。