北京市清华大学中学生标准学术能力诊断性测试2019年11月测试理科数学试卷(二卷)

中学生标准学术能力诊断性测试2019 年9月测试理科综合试卷本试卷共300 分，考试时间150 分钟。

可能用到的相对原子质量：H—1 C—12 N—14 O—16 Mn—55 C a—40一、选择题：本题共13 小题，每小题6分，共78 分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．下列不能为生物界具有统一性提供证据的是：A．所有生物合成蛋白质的场所都相同且共用一套密码子B．所有生物都以具有特定核苷酸序列的核酸携带遗传信息 C．所有生物都以A TP 和A DP的相互转化机制作为能量供应机制 D．所有生物都以有丝分裂或者无丝分裂的方式实现细胞增殖2．狂犬病病毒是一种嗜神经病毒，可由神经-肌肉接点处入侵神经细胞，过程如图所示。

目前疫苗接种是预防和控制狂犬病发病最有效的措施。

狂犬疫苗是将狂犬病毒接种在地鼠肾细胞培养后，收获病毒液，经灭活纯化而成。

下列选项中正确的是：A．神经细胞被狂犬病病毒感染后往往会引起细胞坏死B．吞噬细胞吞噬消化侵入人体的部分病毒，此过程属于人体的第三道防线 C．狂犬病病毒被胞吞进入突触小体并沿着轴突逆行，与神经冲动传导的方向相反D．人被咬伤后可注射狂犬疫苗，以刺激浆细胞产生抗体直接消灭病毒3．最新研究发现外源环磷酸鸟苷 (c G M P)可调控大蒜根尖细胞有丝分裂，实验结果如表所示，据表分析正确的是：A．在显微镜视野中排列紧密呈长方形的细胞属于根尖分生区细胞B．据表可知不同浓度c GMP 溶液可抑制细胞分裂还可抑制染色体畸变 C．剪取根尖2～3cm，进行解离、漂洗、染色、制片后可在显微镜下观察细胞D．若每个根尖装片约统计600 个细胞，这样每种c GMP 浓度下应保证统计7个根尖装片以降低实验误差4．2019 年获诺贝尔生理医学奖的科学家揭示了生物钟的分子控制机制。

他们研究发现，果蝇中的per i od基因有活性时转录并翻译出 PER 蛋A．生物节律是指生命活动以24 小时左右为周期的变动，其控制中枢在大脑皮层B．机体对生物节律的控制存在负反馈调节机制C．PER 和T IM 通过核孔进入细胞核，核孔对大分子的进出具有选择性D．控制T IM 合成的t imless 基因突变后，个体将可能无法感知外界环境的昼夜周期变化5．江苏太湖水体富营养化非常严重，蓝藻疯长。

中学生标准学术能力诊断性测试 2019年11月测试理科综合试卷(一卷)——化学可能用到的相对原子质量：H 1 O 16 Fe 56 Cu 64 S 32一、选择题：本题共13小题，每小题 6分，共78分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1.中华文化源远流长、博大精深。

下列有关蕴含的化学知识的说法中，不正确的是A. 食品包装中常见的抗氧化剂成分为：还原性铁粉、氯化钠、炭粉等，其脱氧原理与钢铁的吸氧腐蚀不相同B. “陶尽门前土，屋上无片瓦。

十指不沾泥，鳞鳞居大厦。

”黏土烧制陶瓷的过程发生了化学变化C. “兰陵美酒郁金香，玉碗盛来琥珀光。

”粮食发酵产生的酒精分散在酒糟中，可以通过蒸馏与酒糟分离D. 侯氏制碱法中的“碱”指的是纯碱2.某有机物结构简式如图,下列关于该有机物的说法正确的是①分子式为C16H14O5；②能使酸性KMnO4溶液褪色；③能发生加成反应，但不能发生取代反应；④苯环上的一溴代物有6种；⑤1mol该有机物水解时最多能消耗4molNaOH；⑥1mol该有机物在一定条件下和H2反应，共消耗6molH2。

A. ①②③⑥B. ①②⑤C. ①④⑤⑥D. ①②④⑤⑥3.W、X、Y、Z 为元素周期表中的主族元素，且原子序数均不大于20，W 的原子序数最大，X 位于第二周期且原子的最外层电子数是内层电子数的2 倍，Y 的单质在空气中易形成一层致密的氧化膜，Z 与Y 同周期且相邻，W、Y 原子的最外层电子数之和等于Z 原子的最外层电子数。

下列说法正确的是A. 简单离子半径：Y＞W＞XB. 最高价氧化物对应水化物的碱性：Y﹤WC. 单质的熔点：Z＞W＞XD. Y、Z 的氧化物均不能溶解于水中，且均为碱性氧化物4.CuSO4是一种重要的化工原料，其制备途径及性质如图所示(假设恰好完全反应)。

下列说法正确的是A. 途径①所用混酸中，H2SO4与HNO3物质的量之比为2:3B. 1molCuSO4在1100℃所得混合气体中，O2为0.75molC. Z 只能是葡萄糖D. 相对于途径①、③，途径②更好地体现了绿色化学思想5.下列装置图的使用说法正确的是A. 甲装置吸收NH3制氨水B. 乙装置需添加其它仪器才能检验其气密性C. 丙装置中，向酸性高锰酸钾溶液中滴加草酸溶液，溶液的紫红色逐渐褪去D. 丁装置收集并吸收多余的HCl6.某工厂采用如图装置处理化石燃料开采、加工过程产生的H2S废气，已知电解池中的两个电极均为惰性电极。

中学生标准学术能力诊断性测试2019年11月测试文科数学试卷(一卷)本试卷共150分，考试时间120分钟。

一、选择题：本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1.己知全集U ＝R ，集合A ＝{x|1x x-≥0}，B ＝{x|y ＝lg(3x －1)}，则A ∩(U ðB)＝ A.(0，1] B.(0，13] C.(13，1] D.(－∞，13] 2.己知a ∈R ，复数z ＝23a i i-+(i 为虚数单位)，若z 为纯虚数，则a ＝ A.23 B.23- C.6 D.－6 3.某单位200名职工的年龄分布情况如图所示，现要从中抽取25名职工进行问卷调查，若采用分层抽样方法，则40～50岁年龄段应抽取的人数是A.7B.8C.9D.104.下列函数中，在区间(0，＋∞)上单调递增的是A.y ＝3－xB.y ＝log 0.5xC.21y x =D.12x y x +=+ 5.已知抛物线y 2＝4x 的焦点为F ，直线l 过点F 与抛物线交于A 、B 两点，若|AF|＝3|BF|，则|AB|＝A.4B.92 C.132 D.1636.己知1tan()43πα-=-，则sin(2)2sin()cos()2παπαπα+--+= A.75 B.15 C.15- D.31257.设变量x 、y 满足约束条件20240240x y x y x y +-≥⎧⎪-+≥⎨⎪--≤⎩，且z ＝kx ＋y 的最大值为12，则实数k 的值为A.－2B.－3C.2D.38.在△ABC 中，角A ，B ，C 的对边分别为a ，b ，v ，若a ＝1，c ＝bsinA ＝asin(3π－B)，则sinC ＝9.某三棱锥的三视图如图所示，网格纸上小正方形的边长为l ，则该三棱锥外接球的表面积为A.27πB.28πC.29πD.30π10.函数13cos 6x y x e =-的大致图象是11.已知双曲线C ：22221(0,0)x y a b a b-=>>的右焦点为F ，直线l ：yx 与C 交于A ，B 两点，AF ，BF 的中点分别为M ，N ，若以线段MN 为直径的圆经过原点，则双曲线的离心率为A.3－12＋112.在△ABC 中，AB ＝8，AC ＝6，∠A ＝600，M 为△ABC 的外心，若AM AB AC λμ=+，λ，μ∈R ，则4λ＋3μ＝A.34B.53C.73D.83二、填空题：本大题共4小题，每小题5分，共20分。

清华大学中学生标准学术能力诊断性测试2019年11月测试卷语文作文材料、导写及范文太和一中李岩2019.11.10阅读下面的材料，根据要求写作。

(60分)高考过后，一位母亲在某知名社交平台上提出了一个问题：“我家是普通的工薪阶层，女儿刚刚参加完高考，高三这一年，她非常努力，没日没夜复习功课，我们都很心疼女儿。

考完之后，她终于有一种解脱感，而且感觉考得不错，就打算用我们奖励她的5万元买一个奢侈品牌包包，作为家长该怎么办呢?”网友纷纷为其支招，有的回帖说高三一年确实辛苦，奖励一下也理所当然；有的认为物质奖励并不是最好的教育方式。

你怎么看待这个家庭问题？要求：综合材料内容及含意，自选角度，确定立意，明确文体，自拟标题，不要套作，不得抄袭:不少于800字。

作文材料分析：从作文所给材料要求来看，属于新材料的任务驱动性作文；从立意来角度看，考生可以考虑以下几个方面:（1）建议“母亲”不要采用物质奖励的方式激励孩子。

（2）劝“母亲”、并阐述理性消费的意义与办法。

（3）辩证看待这个问题，建议“母亲”懂得体谅、理解女儿，不伤害女儿的自尊心等。

附范文：合理，方有利太和一中李岩提供普通工薪阶层的家长，用5万元奖励她高考过后的女儿，或许让人们尚可理解，毕竟“再苦不能苦孩子“已渗入人心。

但女儿却要用这5万元买一个奢侈品牌的包包，这就匪夷所思。

不禁使人质疑这种奖励及消费的合理性了，对孩子的成长是否有利？考了好成绩，奖励个玩具；帮妈妈做家务，奖励个零花钱。

生活中司空见惯。

“期末考得好的话，带你出去旅游”“考入重点高中，给你5000块钱！”“高考被985/211录取，给你2万块。

”相信这些事、这些话，就可能发生你的家庭或你的身边。

奖励是对一个行为的回报。

但家长仅用钱来回报孩子的努力，就会使孩子产生对金钱的盲目崇拜，是弊大于利的。

常用金钱奖励孩子，最终只能害了孩子。

所以理性的家长，多用金钱为孩子的健康成长提供基本条件，而不是让孩子在挥霍金钱中消磨意志，自毁前程。

中学生标准学术能力诊断性测试2019年11月测试理综综合生物试题1.美国免疫学家詹姆斯·艾利森和日本免疫学家本庶佑因发现了用于治疗癌症的免疫调节抑制策略而获得了2018年诺贝尔生理学或医学奖。

他们发现在T细胞表面有CTLA-4蛋白，在识别目标并接受启动信号时，使T细胞活性降低，起到免疫刹车作用，从而减弱对癌细胞的攻击，以下理解错误的是A. CTLA-4的形成需要T细胞内的核糖体、内质网、高尔基体参与B.同一个体中的癌细胞与T细胞的核基因是不同的C.可通过注射CTLA-4抗体的方式，使癌细胞逃脱免疫系统的监控D.癌细胞被攻击清除主要依靠细胞免疫产生的效应T细胞，此过程属于细胞凋亡2.最新研究发现“细胞外烟酞胺磷酸核糖转移酶” (eNAMPT，蛋白质类)不仅能延长小鼠的寿命，还逆转了老鼠身体机能的衰老，这一研究可让人的“返老还童”成为可能。

有关酶的说法错误的是A.eNAMPT可与双缩服试剂反应产生紫色络合物.高温变性后仍能与该试剂变色B.eNAMP T可降低反应的活化能，可在最适温度和最适pH条件下保存C.eNAMPT由基因控制合成，影响代谢进而控制生物的性状D.eNAMPT的催化具有高效性和专一性，其作用的发挥离不开特定的空间结构3.细胞信号转导是指细胞通过受体感受信息分子的刺激，经胞内信号转导系统转换，从而影响细胞生物学功能的过程。

下图表示两种细胞信号转导形式，有关叙述错误的是A.甲图的激素可以表示性激素，以自由扩散的方式穿膜，与细胞膜的基本支架有关B.甲图可说明信息分子可影响基因表达过程，②③的碱基互补配对方式不同C.甲图中的d基本骨架为独特的双螺旋结构.e为mRNA可作为翻译的模板D.乙图可以反应细胞膜具有细胞间的信息交流的功能，图中的受体化学本质为糖蛋白4.下表为适宜浓度的a-萘乙酸(NAA)和赤霉素(GA3)溶液对燕麦胚芽鞘生长的影响，据表分析，下列说法错误的是B.若实验用的NAA浓度为l，则改用低于m浓度的NAA时，胚芽鞘长度不一定减少C.NAA与GA3可调节植物基因表达，二者混合使用具有协同作用D.NAA与GA3是由植物产生，由产生部位运输到作用部位且具有微量而高效的特点5.将果蝇的一个精原细胞放在3H标记的胸腺嘌呤脱氧核酸的培养液中培养完成减数分裂产生精子。

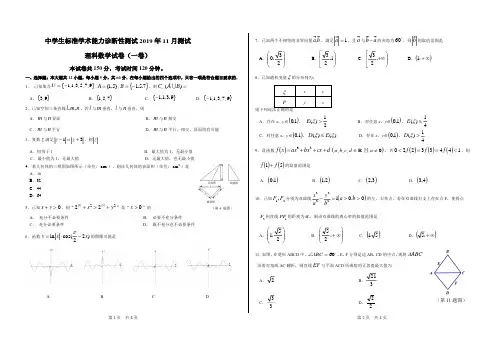
中学生标准学术能力诊断性测试2019年11月测试理科数学试卷（一卷）本试卷共150分，考试时间120分钟。

一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1． 已知集合{}1,1,3,5,7,9U =−,{1,5}A =,{}7,5,1−=B ，则()U C A B =A ．{}3,9 B ．{}1,5,7 C ．{}1,1,3,9− D ．{}1,1,3,7,9−2．已知空间三条直线n m l ,,，若l 与m 垂直，l 与n 垂直，则A ．m 与n 异面B ．m 与n 相交C ．m 与n 平行D ．m 与n 平行、相交、异面均有可能 3．复数z 满足31+=−z z ，则zA ．恒等于1B ．最大值为1，无最小值C ．最小值为1，无最大值D ．无最大值，也无最小值 4．某几何体的三视图如图所示（单位：cm ），则该几何体的表面积（单位：2cm ）是 A ．16 B ．32 C ．44D ．64 5．已知0>+y x ，则“2||2||22y x y x +>+”是“0>x ”的A ． 充分不必要条件B ． 必要不充分条件C ． 充分必要条件D ． 既不充分也不必要条件 6．函数ln cos(2)2y x x π=⋅−的图像可能是A B C D7．已知两个不相等的非零向量b ,a ，满足1=a ，且a 与a b −的夹角为 60，则b的取值范围是A ．⎪⎪⎭⎫ ⎝⎛230，B ．⎪⎪⎭⎫⎢⎣⎡1,23C ．⎪⎪⎭⎫⎢⎣⎡+∞,23 D ．()∞+，1 8．已知随机变量ξ的分布列为：ξx y Pyx则下列说法正确的是 A ．存在x ，y ()1,0∈，1()2E ξ>B ．对任意x ，y ()1,0∈，1()4E ξ≤C ．对任意x ，y ()1,0∈，()()DE ξξ≤ D ．存在x ，y ()1,0∈，1()4D ξ>9．设函数()d cx bx ax x f +++=23(),,,0a b c d a ∈≠R 且，若()()()14433220<==<f f f ，则()()51f f +的取值范围是A ．()10， B ．()21，C ．()3,2D ．()4,3 10．已知21,F F 分别为双曲线()0012222>>=−,b a by a x 的左、右焦点，若在双曲线右支上存在点P ，使得点2F 到直线1PF 的距离为a ，则该双曲线的离心率的取值范围是A ．⎪⎪⎭⎫⎝⎛251， B ．⎪⎪⎭⎫ ⎝⎛∞+，25 C ．()51， D ．()∞+，511．如图，在菱形ABCD 中，60ABC∠=，E ，F 分别是边AB ，CD 的中点，现将ΔABC沿着对角线AC 翻折，则直线EF 与平面ACD 所成角的正切值最大值为A ．2 B ．321C ．33 D ．22（第11题图）12．已知数列}{n a 满足11=a ，11ln 1++=+nn n a a a ，记[][][]n n a a a S +++= 21，[]t 表示不超过t 的最大整数，则2019S 的值为A ．2019B ．2018C ．4038D ．4037 二、填空题：本大题共4小题，每小题5分，共20分． 13．在[]2,2−上随机地取一个实数k ，则事件“直线kx y =与圆()9522=+−y x 相交”发生的概率为 ．14．如图，在ABC ∆中，AC AB >，32=BC ，︒=60A ，ABC ∆的面积等于32，则角平分线AD 的长等于 ．15．已知数列}{n a 满足n a a n n 2151−=++，其前n 项和为n S ，若n S 8S ≤恒成立，则1a 的取值范围为 ．16．已知P 为椭圆C ：22+143x y =上一个动点，1F 、2F 是椭圆C 的左、右焦点，O 为坐标原点，O 到椭圆C 在P 点处的切线距离为d ，若12247PF PF ⋅=，则d = ． 三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．第17~21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答． （一）必考题：60分． 17．（12分）已知函数x x x f cos 3sin )(−=（1）求函数()f x 的单调递增区间；（2）在ABC ∆中，角,,A B C 所对的边分别是a ,b ,c ，若()3f B =，3b =，求ABC∆面积的最大值．18．（12分）如图，已知四棱锥P —ABCD 中，底面ABCD 是直角梯形，AD //BC ，BC =2AD ，AD ⊥CD ，PD ⊥平面ABCD ，E 为PB 的中点． （1）求证：AE //平面PDC ；（2）若BC =CD =PD ，求直线AC 与平面PBC 所成角的余弦值．19．(12分) 已知甲盒内有大小相同的2个红球和3个黑球，乙盒内有大小相同的3个红球和3个黑球，现从甲，乙两个盒内各任取2个球．（1）求取出的4个球中恰有1个红球的概率；（2）设ξ为取出的4个球中红球的个数，求ξ的分布列和数学期望．20．(12分)如图，斜率为k 的直线l 与抛物线24y x =交于A 、B 两点，直线PM 垂直平分弦AB ，且分别交AB 、x 轴于M 、P ，已知()4,0P ． （1）求M 点的横坐标；（2）求PAB △面积的最大值．21．（12分）已知函数xaxx x f −=ln )(，R a ∈． （1）若函数)(x f 有且只有两个零点，求实数a 的取值范围；（2）设函数)(x f 的两个零点为21,x x ，且21x x ≠，求证e x x 221>+．（二）选考题：共10分．请考生在第22,23题中任选一题作答，如果多做，则按所做的第一题计分．作答时请写清题号．22．[选修4—4：坐标系与参数方程]（10分） 在平面直角坐标系xOy 中，曲线C 的参数方程为4cos 2sin x y αα=⎧⎨=⎩（α为参数），在以坐标原点O 为极点，x 轴的正半轴为极轴的极坐标系中，点P 的极坐标为4,3π⎛⎫ ⎪⎝⎭，直线l 的极坐标方程为2sin 96ρθπ⎛⎫−= ⎪⎝⎭． （1）求直线l 的直角坐标方程与曲线C 的普通方程；（2）若Q 是曲线C 上的动点，M 为线段PQ 的中点，直线l 上有两点A,B ，始终满足AB 4=，求MAB △面积的最大值与最小值．23．[选修4—5：不等式选讲]（10分）已知c b a ,,为正实数，且满足3=++c b a ．证明：（1）3≤++ac bc ab ； （2）3222≥++ac c b b a ．（第14题图）l中学生标准学术能力测试诊断性测试2019年11月测试理科数学（一卷）答案一． 选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只二． 填空题：本大题共4小题，每小题5分，共20分． 13．3814．315． (,7]−∞16．2三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．第17~21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答． （一）必考题：60分．17．解：()sin 2sin()3f x x x x π==− ………………………………2分（1）令22232k x k πππππ−≤−≤+（k Z ∈）得52266k x k ππππ−≤≤+（k Z ∈） 故函数()f x 的单调递增区间为52,266k k ππππ⎡⎤−+⎢⎥⎣⎦（k Z ∈） …………………5分（2）由()f B = ，得sin()3B π−=323πππ+=−k B 或,3223πππ+=−k B∴222,3B k B k k Z ππππ=+=+∈或 ，32π=∴B B 是三角形的内角， ． ………………………………7分∵B ac c a b cos 2222−+= ∴922=++ac c a∴92≤+ac ac ，即3≤ac ………………………………9分 ∴133sin 24ABC S ac B ∆=≤． ………………………………11分 当且仅当3a c == 时，ABC ∆面积的最大值是334． ……………………………12分 18．（1）取PC 的中点F ，连接DF ，EF ， ∵ E 是PB 的中点， ∴ EF //BC ，且BC =2EF ， 又 AD //BC ，BC =2AD∴ AD //EF 且AD =EF ， ………………………………2分 ∴ 四边形ADFE 是平行四边形，∴ AE //DF ，又DF ⊂平面PDC ,AE PCD ⊄平面 ， ……………………………… 4分 ∴ AE //平面PDC ． ………………………………5分 （2）若PD =DC ，则△PDC 是等腰三角形， ∴ DF ⊥PC ，又AE //DF ，∴ AE ⊥PC∵ PD ⊥平面ABCD ，BC ⊂平面ABCD ∴ PD ⊥BC ， 又 BC ⊥CD ,CDPD D = ∴ BC ⊥平面PDC ， ………………………………7分 ∵ DF ⊂平面PDC ∴ BC ⊥DF ∴ BC ⊥AE 又 AE ⊥PC ,PCBC C =∴ AE ⊥平面PBC ， ………………………………9分 连接EC ，AC ，则∠ACE 就是直线AC 与平面PBC 所成的角． ………………………10分 设PD =CD =BC =2，EBAPCD F在Rt △PCB 中，求得PC=，PB= ，EC在Rt △ADC 中，求得AC∴ 在Rt △AEC中，c s o EC ECA AC ==∠． ………………………………12分19．（1）设事件i A 为“甲盒中取出i 个红球”，事件j B 为“乙盒中取出j 个红球”则()()2223332256,i ij ji j C C C C P A P B C C −−== 设事件C 为“4个球中恰有1个红球”()()()021111022333233301102222565639633C 1015101510C C C C C C C C P P A B P A B C C C C ∴=+=⋅+⋅=⋅+⋅=…………………………………3分（2）ξ可取的值为0,1,2,34，()()02022333002256C C C C 30B =C C 50P P A ξ∴===⋅ ……5分 ()()31C 10P P ξ===()()()()022011112002233323332333021120222222565656112++25C C C C C C C C C C C C P P A B P A B P A B C C C C C C ξ==+=⋅+⋅⋅=………………………………7分()()()112020112333233312212222565693++50C C C C C C C C P P A B P A B C C C C ξ===⋅⋅= …………………9分()()20202333222256C C C C 14B =C C 50P P A ξ∴===⋅ ………………………………10分的分布列为：33119190123+450102550505E ξ∴=⨯+⨯+⨯+⨯⨯= ………………………………12分20．（1）设112200(,),(,),(,)A x y B x y M x y ，则121200,22x x y y x y ++==，……1分 ∴ 121212042y y k x x y y y −===−+ ， ………………………………3分而004MP y k x =−， ………………………………4分 由1MP k k ⋅=− 得042x −=− ，即02x =． ………………………………5分（2）设直线0:()2AB x m y y =−+ 即0:2AB x my my =−+ ， 与抛物线24y x = 联立得204480y my my −+−= ，220164(48)0,2m my m =−−>∴<△则121204,48y y m y y my +==−， ………………………………7分所以12|||AB y y =−=， 而P 到直线AB的距离为d =所以01||2|22PAB S d AB my ∆==+ ………………………………9分 又由于012y m k ==，所以222(24(PAB S m m ∆=+=+（22m <）， …………………10分t =，则0t >且222m t =−， 所以234(3)124PAB S t t t t ∆=−=− ， 令3()124(0)g t t t t =−> ，则2()121212(1)(1)g t t t t '=−=−+，当01t << ，()0g t '> ，当1t >时，()0g t '<，故3()124(1)8g t t t g =−≤=，即PAB ∆面积的最大值为8． ………………………12分21．（1）解：21ln ')0,xf x x e x−==∴=（ 当')00,()0)f x x e f x e ><<∴（时，在（，上单调递增 ， 当')0,(),)f x x e f x e <>∴+∞（时，在（上单调递减． 1)()f x f e a e∴==−极大值（ ……3分，1)0f x a e∴<<（有且只有两个零点，，00()0x x f x >→<又且时，0()0x a f x →+∞=>时，若时，不符合题意，0lim ()0x a f x a →+∞<=−>若时,不符合，0lim ()0x a f x a →+∞>=−<若时,满足，综上，若使()f x 有且只有两个零点，10a e∴<< …………………… 4分 （2）证法一：ln ln )0ln ,ln x xf x a x ax x a e x=−=∴=∴=⋅（，，12ln ,ln x x x xe a −∴=是的两根 tt e t t g e t t g x t x t −−−=⋅===)1()(',)(,ln ,ln 2211设，上单调递减上单调递增，在，在（),1[]1-)(+∞∞∴t g ， ………………………………6分,10,),()(212121t t t t t g t g <<<<=则必有设 ），（构造函数10),1()1()(G ∈−−+=t t g t g t ，,01-()1(')1(')(G'21>=−++=+）tt e ett g t g t,0)0()(,)1,0()(G =>∴∈∴G t G t t 上单调递增在 ………………………………9分)()()2(211t g t g t g =>−∴，上单调递减，在又),1()(),,1(,221+∞∈+∞∈−t t g t t 2,-22121>+∴<∴t t t t ,12ln ln 2x x ∴+>，即212x x e ⋅>；122x x e +∴>>，即122x x e +>．……12分 证法二：不妨设121x e x <<<，)()(21x f x f = ，1212ln ln x x x x ∴=，即2211ln ln x x x x ∴=， ………………………………6分设21(1)x tx t => ，1111ln ln ln ln ln tx t x t x x +∴==，1ln ln 1t x t ∴=−， 1ln 1ln ln ln ln )ln(ln 112−=−+=+==t t t t t t x t tx x ，t t t x x ln 11ln ln 21⋅−+=+∴，122x x +> ，要证122x x e +>，只需证212x x e ⋅>， 即证121ln ln ln 21t x x t t ++=⋅>− ，即证2(1)ln 01t t t −−>+． …………………………9分 设2(1)()ln ,(1)1t g t t t t −=−>+， 22214(1)'()0(1)(1)t g t t t t t −=−=>++，()g t ∴在(1,)+∞单调递增． 0)1(=g ，0)1()(=>∴g t g ，12ln ln 2x x ∴+>，122x x e +∴>>，即122x x e +>．………………………12分 证法三：不妨设121x e x <<<，12()()f x f x =，1212ln ln x x x x ∴=， ………………………………6分 要证122x x e +>，只需证122112112ln ln ln x x x x xe x x x +−>=>− ， ……………………7分 变形，得：2121212()ln ln x x x x x x −−>+，即2212112(1)ln 1x x x x x x −>+．设212(1)ln (1)1x t t t t x t −=∴>>+ ，设2(1)()ln ,(1)1t g t t t t −=−>+，……………………10分 22214(1)'()0(1)(1)t g t t t t t −=−=>++，()1g t ∴+∞在（，）上单调递增， ()(1)0g t g ∴>=，12112ln x x xe x +∴>=成立，122x x e ∴+>．………………………12分（二）选考题：共10分．请考生在第22，23题中任选一题作答，如果多做，则按所做的第一题计分．作答时请写清题号． 22．【选修4−4：坐标系与参数方程】（10分） （1）因为直线l 的极坐标方程为2sin 96ρθπ⎛⎫−= ⎪⎝⎭，即12sin cos 922ρθθ⎛⎫−⋅= ⎪ ⎪⎝⎭．由cos ,sin x y ρθρθ==，可得直线l 的直角坐标方程为90x +=． ………………………………2分将曲线C 的参数方程4cos 2sin x y αα=⎧⎨=⎩，消去参数a ，得曲线C 的普通方程为224161x y +=． ………………………………4分（2）设()Q 4cos ,2sin αα ，[)0,2απ∈ ．点P 的极坐标4,3π⎛⎫⎪⎝⎭，化为直角坐标为(2, ．则(M 2cos +1,sin αα+． ………………………………6分所以点M 到直线l 的距离d ==，（其中，tan θ=），所以77d 22⎡+∈⎢⎣⎦ ………………………………8分AB 4= ，12772ΔMAB S AB d d ⎡∴=⋅=∈−⎣ ∴MAB △面积的最大值为77+，最小值为77− …………………………10分23．【选修4−5：不等式选讲】（10分）23．（1）因为,,a b c 为正实数，且满足3a b c ++=．所以，()bc ac ab c b a c b a 2222222+++++=++ac c bc,a c ab,b b a 222222222≥+≥+≥+ ，ac bc ab c b a ++≥++∴222 ……2分()2333a b c ab ac bc ∴++≥++ ，3a b c ++=，∴3ab bc ac ++≤，当且仅当a b c ==时，等号成立 ………………………………5分（2）2222,2,2a b c b a c b a c b c a+≥+≥+≥ ， ()2222a b c a b c a b c b c a ∴+++++≥++ ………………………………8分222a b c a b c b c a ∴++≥++ ，3a b c ++= ，2223a b c b c a∴++≥ ，当且仅当a b c == 时，等号成立 ………………………………10分。

中学生标准学术能力诊断性测试 2018 年 11 月测试理科综合试卷（一卷）本试卷共 300 分，考试时间 150 分钟。

可能用到的相对原子质量：锆（Zr ）-91 Cl-35.5 O-16 Si-28 Ge-73一、选择题：本题共 13 小题，每小题 6 分，共 78 分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．关于细胞内所含有的“骨架”说法错误的是： A ．“细胞的蓝图—DNA”的骨架是磷酸和脱氧核糖交替连接构成的 B ．多糖、蛋白质、核酸等生物大分子都以碳链为骨架C ．单糖、氨基酸、核苷酸等单体也以若干个相连的碳原子构成的碳链为基本骨架D ．真核细胞中维持细胞形态的细胞骨架是由蛋白质和磷脂构成的网架结构2．右图是物质进出细胞的运输方式示意图，以下有关说法正确的是：A ．胰岛素通过丁图所示过程进入细胞发挥作用B ．通过丙图出细胞的物质并不一定是大分子C ．甲图所示跨膜方式使膜两侧离子趋于平衡D ．乙图所示过程与小肠绒毛上皮细胞吸收葡萄糖的方式相同3．自 2017 年 7 月以来，宫颈癌疫苗（HPV 疫苗）在国内得到推广。

该疫苗是 HPV （DNA 病毒，宿主细胞为上皮细胞）灭活纯化制备，接种三针可预防宫颈癌症的发生，下列说法错误的是： A ．HPV 的核酸彻底水解后可以获得 6 种化合物B ．若想用 32P 标记 DNA 可把 HPV 培养在含 32P 的磷酸盐溶液里C ．若想验证 HPV 遗传物质是 DNA ，可用含有同位素标记的 T 或 U 的上皮细胞来培养病毒，观察其子代病毒的放射性D ．HPV 侵入人体后，大多数情况下人体可以通过体液免疫和细胞免疫来清除病毒4．美国生物学家发现 1-甲基环丙烯（1-MCP ）可作为保鲜剂用于储存果蔬。

科学家用适宜浓度 1-MCP 对柿子果实的细胞呼吸速率和乙烯产生量的影响进行了研究，结果如图。

请据图选出错误的是：A ．由图甲可推测，1-MCP 可能抑制呼吸酶来减弱细胞呼吸延迟呼吸高峰的到来，从而对果蔬进行保鲜，降低果蔬营养物质的损耗B ．由图乙可推测，1-MCP 是通过抑制乙烯的产生延长了果蔬的储运期C ．研究发现柿子细胞表面乙烯受体数量正常，1-MCP 可能优先结合乙烯受体，抑制果蔬对乙烯的反应，延缓果蔬成熟D ．农业生产上可在一开始坐果时立即使用 1-MCP ，使果实延迟成熟上市5．生态果园是利用生态工程学原理，科学配置各成分及资源而建立的可持续发展的果园生产体系。

高三第二学期入学检测试卷数学(理)一、选择题（共8小题；共8×5＝40分）1.已知复数z 满足()1i z i +=，i 为虚数单位，则z 等于（ ）A. 1i -B. 1i +C.1122i - D.1122i + 【答案】A 【解析】因为|2(1)11(1)(1)i i z i i i i -===-++-，所以应选答案A ． 2.已知圆的极坐标方程为4sin 4P πθ⎛⎫=-⎪⎝⎭，则其圆心坐标为（ ） A. 2,4π⎛⎫⎪⎝⎭B. 32,4π⎛⎫ ⎪⎝⎭ C. 2,4π⎛⎫-⎪⎝⎭D. ()2,0【答案】B 【解析】 【分析】把圆的极坐标方程化为直角坐标方程，求得圆心坐标(，再根据极坐标与直角坐标的互化公式，即可求解.【详解】由题意知，圆的极坐标方程为4sin 4πρθ⎛⎫=-⎪⎝⎭，即ρθθ=-，即2sin cos ρθθ=-，所以220x y ++-=，所以圆心坐标为(，又由cos sin x y ρθρθ=⎧⎨=⎩，可得圆心的极坐标为3(2,)4π，故选B . 【点睛】本题主要考查了极坐标与直角坐标的互化，及圆的方程应用，其中解答中熟记极坐标与直角坐标的互化公式，把极坐标化为直角坐标方程是解答的关键，着重考查了运算与求解能力，属于基础题.3.执行如图所示的程序框图，则输出的S 值为（ ）A. 4B. 3C. 2-D. 3-【答案】A 【解析】执行程序框图，2i = ，第一次循环，2;s = 3i = ，第二次循环，1;s =-4i = ，第三次循环，3;s =5i = ，第四次循环，2;s =-6i = ，第五次循环，4;s =7i = 结束循环，输出4,s =故选A.【方法点睛】本题主要考查程序框图的循环结构流程图，属于中档题. 解决程序框图问题时一定注意以下几点：(1) 不要混淆处理框和输入框；(2) 注意区分程序框图是条件分支结构还是循环结构；(3) 注意区分当型循环结构和直到型循环结构；(4) 处理循环结构的问题时一定要正确控制循环次数；(5) 要注意各个框的顺序,（6）在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可. 4.设a ，b ∈R ，则“（a ﹣b ）a 2＜0”是“a ＜b ”的（ ）条件 A. 充分不必要 B. 必要不充分 C. 充要 D. 既不充分也不必要【答案】A 【解析】 【分析】根据不等式的关系，结合充分条件和必要条件的定义进行求解即可.【详解】由（a ﹣b ）a 2＜0得到：0,0a a b ≠-<，则a ＜b 成立，即充分性成立，反之不成立，故为充分不必要条件. 故选：A【点睛】本题考查了不等式的关系，充分必要条件，考查了学生逻辑推理，数学运算的能力，属于基础题.5.将一枚硬币连续抛掷n 次，若使得至少有一次正面向上的概率不小于1516，则n 的最小值为（ ） A. 4 B. 5C. 6D. 7【答案】A 【解析】由题意得1151()4216nn -=⇒= ,选A. 6.自点 A （﹣3，4）作圆（x ﹣2）2+（y ﹣3）2＝1的切线，则A 到切点的距离为（ ）B. 3D. 5【答案】D 【解析】 【分析】求出圆心和半径，求出AC 的值，可得切线的长度.【详解】圆（x ﹣2）2+（y ﹣3）2＝1表示以C (2,3)为圆心，1为半径的圆，由于AC =且A,C,切点三个点构成以切点为直角顶点的直角三角形，5= 故选：D【点睛】本题考查了圆的切线长求解，考查了学生转化与划归，数学运算的能力，属于基础题.7.某几何体三视图如图所示，在该几何体的体积是（ ）A.103B.203C.25D.45【答案】B 【解析】 【分析】由三视图，可得该几何体为四棱锥，由体积公式即得解.【详解】如图所示，该几何体为四棱锥，其中PA ⊥平面ABCD ，作BE CD ⊥，垂足为E 底面可以看成直角梯形ADEB 和直角三角形BEC 构成， 则：1121204(222)3223V +=⨯⨯⨯+⨯⨯= 故选：B【点睛】本题考查了三视图及棱锥的体积，考查了学生空间想象，运算求解能力，属于基础题.8.已知点(),P x y 是平面区域()4{04y x y x m y ≤-≤≥-内的动点, 点()1,1,A O -为坐标原点, 设()OP OA R λλ-∈u u u r u u u r的最小值为M ,若2M ≤恒成立, 则实数m 的取值范围是（ ）A. 11,35⎡⎤-⎢⎥⎣⎦B. 11,,35⎛⎤⎡⎫-∞-⋃+∞ ⎪⎥⎢⎝⎦⎣⎭C.1,3⎡⎫-+∞⎪⎢⎣⎭ D.1,2⎡⎫-+∞⎪⎢⎣⎭【答案】C【解析】试题分析：直线()4x m y=-恒过定点(0,4)，当0m>时，约束条件()4{04yx yx m y≤-≤≥-对应的可行域如图，则()OP OA Rλλ-∈u u u r u u u r的最小值为0M=，满足2M≤，当0m=时，直线()4x m y=-与y轴重合，平面区域()4{04yx yx m y≤-≤≥-为图中y轴右侧的阴影区域，则()OP OA Rλλ-∈u u u r u u u r的最小值为0M=，满足2M≤，当0m<时，由约束条件()4{04yx yx m y≤-≤≥-表示的可行域如图，点P与点B重合时，()OP OA Rλλ-∈u u u r u u u r的最小值为M OB=u u u r，联立{(4)y xx m y==-，解得44(,)11m mBm m--，所以421mOBm=-u u u r，由4221mm≤-，解得1135m-≤≤，所以13m-≤≤，综上所述，实数m的取值范围是1,3⎡⎫-+∞⎪⎢⎣⎭，故选C.考点：简单的线性规划.【方法点晴】本题主要考查了二元一次不等式组所表示的平面区域、简单的线性规划求最值问题，着重考查了数形结合思想方法及分类讨论的数学思想方法的应用，关键是正确的理解题意，作出二元一次不等式组所表示的平面区域，转化为利用线性规划求解目标函数的最值，试题有一定的难度，属于难题.二、填空题（共6小题；共6×5＝30分） 9.在等差数列{}n a 中，若()246n n a a n n N *++=+∈,则该数列的通项公式na=_____【答案】21n + 【解析】 【分析】由已知条件可得数列的首项和公差，可得通项公式.【详解】解：设等差数列{}n a 的公差为d ，由246n n a a n ++=+ ①， 可得24414n n a a n +++=+ ② ，可得②-①，48n n a a +-=，可得2d =， 把1n =代入①，可得12410a +=，可得13a =， 可得数列的通项公式32(1)21n a n n =+-=+， 故答案：21n +.【点睛】本题考查等差数列的通项公式，求出数列的首项和公差是解题的关键.10.102a x ⎫⎪⎭展开式中的常数项为180，则a =_________．【答案】2或2- 【解析】 【分析】先求出二项式展开式的通项公式，再令x 的幂指数等于0，求得r 的值，即可求得展开式中的常数项的值，再根据常数项的值为180，求得a 的值．【详解】2a x ）10展开式中的通项公式为 T r+1=10r C •a r •552r x -， 令5﹣52r =0，求得r=2，可得它的常数项为a 2•210C =180，故a=±2， 故答案为2或2-【点睛】求二项展开式有关问题的常见类型及解题策略(1)求展开式中的特定项.可依据条件写出第r ＋1项，再由特定项的特点求出r 值即可. (2)已知展开式的某项，求特定项的系数.可由某项得出参数项，再由通项写出第r ＋1项，由特定项得出r 值，最后求出其参数.11.若函数π()2sin(2)(0)2f x x ϕϕ=+<<的图象过点，则函数()f x 在[0,]π上的单调减区间是____． 【答案】π7π(,)1212(或π7π[,]1212) 【解析】函数()()π2sin 2(0)2f x x ϕϕ=+<<的图象过点(，则2sin ϕ=sin ϕ= ，0,23Q ππϕϕ<<∴=，()2sin(2)3f x x π∴=+.0x π≤≤Q ,022x π∴≤≤,72333x πππ≤+≤,有于sin y x =在3[,]22ππ为减函数，所以32232x πππ≤+≤，解得71212x ππ≤≤.【点睛】根据函数图象过已知点，求出sin ϕ ，借助ϕ的范围求出ϕ的值.求三角函数在某一区间上的最值及单调区间时，务必要注意“范围优先原则”，根据x 的范围研究x ωϕ+的范围，有时还要关注A 的符号，因此当自变量有范围限制时，解题更要小心失误.12.经过点(2,2)A -且与双曲线2212x y -=有公共渐近线的双曲线方程为_________．【答案】22124x y -=【解析】由题意设所求双曲线的方程为22(0)2x y λλ-=≠，∵点()2,2-在双曲线上， ∴4422λ=-=-， ∴所求的双曲线方程为2222x y -=-，即22124y x -=．答案：22124y x -=13.已知非零向量a r ，b r 满足|b r |＝1，b r 与b a r r -的夹角为30°，则|a r|的最小值是_____．【答案】12． 【解析】 【分析】构造满足题意的三角形，根据几何意义求出|a r|的最小值.【详解】根据题意：作,,30o CB a CA b b a BA A ==∴-=∠=u u u r r u u u r r r r u u u r过C 作CD AB ⊥，垂直为D ，则CD 的长度即为|a r|的最小值，1=sin 302o CD CA =，故|a r|的最小值为12故答案为：12【点睛】本题考查了向量的线性运算的应用，考查了学生转化与划归，数形结合，数学运算的能力，属于中档题.14.在平面直角坐标系xOy 中，对于⊙O ：x 2+y 2＝1来说，P 是坐标系内任意一点，点P 到⊙O 的距离S P 的定义如下：若P 与O 重合，S P ＝r ；若P 不与O 重合，射线OP 与⊙O 的交点为A ，S P ＝AP 的长度（如图）．（1）直线2x +2y +1＝0在圆内部分的点到⊙O 的最长距离为_____； （2）若线段MN 上存在点T ，使得： ①点T 在⊙O 内；②∀点P ∈线段MN ，都有S T ≥S P 成立．则线段MN 的最大长度为_____．【答案】 (1). 124- (2). 4 【解析】 【分析】（1）作出对应的图象，由图象可知当直线与2x +2y +1＝0垂直时对应的交点P ，此时P 到⊙O 的距离最长，即得解；（2）分析可得S P ≤1，因此当线段MN 过原点时，当线段MN 过原点时，MN 的最大长度为4，即得解.【详解】作出对应的图象如图：由图象可知当直线与2x +2y +1＝0垂直时对应的交点P ，|OP|取得最小值，此时P 到⊙O 的距离最长， 此时OP 22124822===+，则AP ＝1﹣OP ＝124-． （2）∵点T⊙O 内，∴S T ≤1，∵S T ≥S P 成立，∴S P ≤1，∀点P ∈线段MN ，若P 在圆内，都满足S P ≤1；若P 在圆外，P 必须在以原点为圆心，2为半径的圆的内部（含边界） ∴当线段MN 过原点时，MN 的最大长度为1+2+1＝4，【点睛】本题考查了直线和圆的新定义问题，考查了学生综合分析，转化划归，数形结合，数学运算的能力，属于较难题.三、解答题（共6小题；共80分）15.已知函数()sin()f x A x ωϕ=+，R x ∈（其中ππ0,0,22A ωϕ>>-<<），其部分图像如图所示．（1）求函数()f x 的解析式；（2）已知横坐标分别为1-、1、5的三点,,M N P 都在函数()f x 的图像上，求sin MNP ∠的值．【答案】（1）()sin()44f x x ππ=+；（2）45. 【解析】【详解】试题分析：本题主要考查三角函数的周期、三角函数的图象、余弦定理、平方关系等基础知识，考查学生的分析问题解决问题的能力、读图能力、转化能力、计算能力. 第一问，利用函数图象先看出周期，再利用周期公式得到ω，再利用特殊点（1,1）解出ϕ的值，从而得到()f x 解析式；第二问，先利用1-、1、5的三点,,M N P 都在函数()f x 的图像上，得到,,M N P 点坐标，从而利用两点间距离公式得到边MN 、MP 、PN 的长，利用余弦定理得到cos MNP ∠的值，最后利用平方关系得到sin MNP ∠，法二：还可以利用向量的数量积来计算.试题解析：（1）由图可知，1A =， 最小正周期428,T =⨯=∴2ππ8,.4T ωω===又∵π(1)sin()14f ϕ=+=，且ππ22ϕ-<< ∴ππ3π444ϕ-<+<，πππ,.424ϕϕ+==∴()sin()44f x x ππ=+．（2） 解法一: ∵ππ(1)sin(11)0,(1)sin (11)1,44f f -=-+==+= π(5)sin(51)14f =+=-， ∴(1,0),(1,1),(5,1)M N P --，MN MP PN ==从而3cos 5MNP ∠==-，∵()0,MNP π∠∈，∴4sin 5MNP ∠==. 考点：三角函数的周期、三角函数的图象、余弦定理、平方关系.16.某地区人民法院每年要审理大量案件，去年审理的四类案件情况如表所示：其中结案包括：法庭调解案件、撤诉案件、判决案件等．根据以上数据，回答下列问题． （Ⅰ）在编号为1、2、3的收案案件中随机取1件，求该件是结案案件的概率； （Ⅱ）在编号为2的结案案件中随机取1件，求该件是判决案件的概率；（Ⅲ）在编号为1、2、3的三类案件中，判决案件数的平均数为x ，方差为S 12，如果表中n x =，表中全部（4类）案件的判决案件数的方差为S 22，试判断S 12与S 22的大小关系，并写出你的结论（结论不要求证明）． 【答案】（Ⅰ）9395；（Ⅱ）1229；（Ⅲ）2212S S ＞； 【解析】 【分析】（Ⅰ）此概率模型为古典概型，分别计算在编号为1、2、3的收案案件中随机取1件和取到的是结案案件的方法数，即得解;（Ⅱ）此题仍为古典概型，分别计算对应的事件数，即得解; （Ⅲ）设4类案件的均值为x ，则34x xX x +==,代入运算，得解. 【详解】（Ⅰ）在编号为1、2、3的收案案件中随机取1件， 共有2400+3000+4100＝9500种取法， 其中取到的是结案案件方法数为 2400+2900+4000＝9300种，设“在收案案件中取1件结案案件”为事件A ， 则P （A ）9395=； （Ⅱ）在编号为2的结案案件中随机取1件共有2900种取法， 其中是判决案件有1200种取法， 设“在该结案案件中取1件判决案件”事件B ，则P （B ）1229=； （Ⅲ）2212S S ＞；设4类案件的均值为x ，则34x xX x +== 2214S =[22221234()()()()x x x x x x x x -+-+-+-] 14=[()2222123()()()x x x x x x x x -+-+-+-] 14=[222123()()()x x x x x x -+-+-] 13＜[222123()()()x x x x x x -+-+-]21S =． 【点睛】本题考查了统计与概率综合，考查了学生数据处理，转化划归，数学运算的能力，属于基础题.17.如图，四边形ABCD 与BDEF 均为菱形，∠DAB=∠DBF=60°，且FA=FC ．（Ⅰ）求证：AC⊥平面BDEF ； （Ⅱ）求证：FC∥平面EAD ； （Ⅲ）求二面角A ﹣FC ﹣B 的余弦值． 【答案】（1）见解析（2）见解析（3）155【解析】试题分析：（Ⅰ）设AC 与BD 相交于点O ，连接FO ，因为四边形ABCD 为菱形，所以AC BD ⊥，且O 为AC 中点，由FA FC =，知AC FO ⊥，由此能够证明AC ⊥平面BDEF ；（Ⅱ）因为四边形ABCD 与BDEF 均为菱形，所以//,//AD BC DE BF ，平面//FBC 平面EAD ，由此能够证明//FC 平面EAD ；（Ⅲ）因为四边形BDEF 为菱形，且60DBF ∠=o ，所以DBF ∆为等边三角形，因为O 为BD 中点，所以FO BD ⊥，故FO ⊥平面ABCD ，由,,OA OB OF 两两垂直，建立空间直角坐标系O xyz -，设2AB =，因为四边形ABCD 为菱形，60DAB ∠=o，则2BD =，所以3,0,3CF =u u u v，)3,1,0CB =u u u v，求得平面BFC 的法向量为()1,3,1n =--r ，平面AFC 的法向量为()0,1,0v =v，由此能求出二面角A FCB --的余弦值.试题解析：（Ⅰ）证明：设AC 与BD 相交于点O ，连接FO ．因为四边形ABCD 为菱形，所以AC⊥BD，且O 为AC 中点． 又 FA=FC ，所以 AC⊥FO． 因为 FO∩BD=O， 所以 AC⊥平面BDEF ．（Ⅱ）证明：因为四边形ABCD 与BDEF 均为菱形， 所以AD∥BC，DE∥BF，所以平面FBC∥平面EAD．又FC⊂平面FBC，所以FC∥平面EAD．（Ⅲ）解：因为四边形BDEF为菱形，且∠DBF=60°，所以△DBF为等边三角形．因为O为BD中点，所以FO⊥BD，故FO⊥平面ABCD．由OA，OB，OF两两垂直，建立如图所示的空间直角坐标系O﹣xyz．…（9分）设AB=2．因为四边形ABCD为菱形，∠DAB=60°，则BD=2，所以OB=1，．所以．所以，．设平面BFC的法向量为=（x，y，z），则有，取x=1，得．∵平面AFC的法向量为=（0，1，0）．由二面角A﹣FC﹣B是锐角，得|cos＜，＞|==．所以二面角A﹣FC﹣B的余弦值为．18.已知椭圆E：2xmy2＝1（m＞1）3过点P（1，0）的直线与椭圆E交于A，B不同的两点，直线AA0垂直于直线x＝4，垂足为A0．（Ⅰ）求m的值；（Ⅱ）求证：直线A0B恒过定点．【答案】（Ⅰ）m＝4（Ⅱ）见解析【解析】【分析】（Ⅰ）利用221c b a a=-即可得解；（Ⅱ）设AB方程并与椭圆联立，利用韦达定理化简直线A0B的方程为点斜式形式，得到定点. 【详解】（Ⅰ）∵椭圆E：2xm+y2＝1（m＞1）的离心率为3，∴2213112c ba a m=-=-=⇒m＝4，（Ⅱ）当直线AB与x轴不重合时，设其方程为x＝my+1．A（x1，y1），B（x2，y2），由22144x myx y=+⎧⎨+=⎩⇒（m2+4）y2+2my﹣3＝0．∴12224my ym-+=+，12234y ym-=+．因为A0（4，y1），2124A By ykx-=-，所以直线A0B的方程为：y﹣y1()21244y yxx-=--，⇒y21221212122122144444y y x y y x y yx y xx y y x y y⎛⎫⎛⎫----=-+⋅=+⎪ ⎪----⎝⎭⎝⎭21122122144y y my y y yxx y y⎛⎫--+=+⎪--⎝⎭．∵()121232my y y y =+，∴()121221212154522y y my y y y y y y y --+==---， ∴直线A 0B 的方程为：y 212542y y x x -⎛⎫=- ⎪-⎝⎭，当直线AB 与x 轴重合时，直线A 0B 与x 轴重合， 综上，直线A 0B 恒过定点（52，0） 【点睛】本题考查了直线和椭圆综合，考查了学生转化与划归，综合分析，数学运算的能力，属于较难题.19.设f （x ）＝xe x ﹣ax 2﹣2ax ．（Ⅰ）若y ＝f （x ）的图象在x ＝﹣1处的切线经过坐标原点，求a 的值； （Ⅱ）若f （x ）存在极大值，且极大值小于0，求a 的取值范围． 【答案】（Ⅰ）a 1e =；（Ⅱ）（0，12e ）∪（12e ，1e）． 【解析】 【分析】（Ⅰ）求f '（x ）得到切线斜率，结合直线过原点，即得解;（Ⅱ）分a ≤0，a ＞0两种情况分析导数极值，得到f （ln 2a ）是极大值，由极大值小于0，求a 的取值范围.【详解】（Ⅰ）f '（x ）＝e x +xe x ﹣2ax ﹣2a ＝（x +1）（e x ﹣2a ），f '（﹣1）＝0，f （﹣1）1e=-+a ， 所以由题意得：011ae -+=-，∴a 1e=；（Ⅱ）由（Ⅰ）得，当2a ≤0时，即a ≤0时，e x ﹣2a ≥0， ∴x ＜﹣1，f '（x ）＜0，f （x ）单调递减， x ＞﹣1，f '（x ）＞0，f （x ）单调递增， 所以f （x ）有极小值，无极大值； 当a ＞0，f '（x ）＝0，x ＝﹣1或x ＝ln 2a ， 当ln 2a ＞﹣1时，即a 12e＞， ∴x ∈（﹣∞，﹣1）和 （ln 2a ，+∞），f '（x ）＞0，f （x ）单调递增，当﹣1＜x ＜ln 2a 时，f '（x ）＜0，f （x ）单调递减，所以f （﹣1）为极大值，且f （﹣1）1e =-+a ，由题意得：f （﹣1）＜0，∴112a e e＜＜； 当ln 2a ＜﹣1时，即0＜a 12e＜， ∴x ∈（﹣∞，ln 2a ）和 （﹣1，+∞），f '（x ）＞0，f （x ）单调递增， x ∈（ln 2a ，﹣1），f '（x ）＜0，f （x ）单调递减，所以f （ln 2a ）是极大值，且f （ln 2a ）＝2aln 2a ﹣aln 22a ﹣2aln 2a ＝﹣aln 22a ＜0恒成立；当ln 2a ＝﹣1时，即a 12e=，f '（x ）＝（x +1）2≥0恒成立，f （x ）单调递增，无极值，舍去； 综上所述：符合条件的a 的取值范围：（0，12e ）∪（12e ，1e）．【点睛】本题考查了函数与导数综合，考查了学生综合分析，转化划归，分类讨论的能力，属于较难题.20.如果无穷数列{a n }的所有项恰好构成全体正整数的一个排列，则称数列{a n }具有性质P ．（Ⅰ）若a n 12112n n k n n k +=-⎧=⎨-=⎩，，（k ∈N *），判断数列{a n }是否具有性质P ，并说明理由， （Ⅱ）若数列{a n }具有性质P ，求证：{a n }中一定存在三项a i ，a j ，a k （i ＜j ＜k ）构成公差为奇数的等差数列；（Ⅲ）若数列{a n }具有性质P ，则{a n }中是否一定存在四项a i ，a j ，a k ，a l ，（i ＜j ＜k ＜l ）构成公差为奇数的等差数列？证明你的结论．【答案】（Ⅰ）数列{a n }具有性质P ．见解析（Ⅱ）见解析（Ⅲ）不一定存在，见解析 【解析】 【分析】（Ⅰ）分n 为奇数，n 为偶数讨论，研究a n 包含的数的情况，即得解;（Ⅱ）考虑12,,...,m a a a ，令12max{,,...,}m M a a a =，从1m a +开始寻找第一个大于M 的项，记为：j a ,分j a 为奇数，偶数讨论，分别构造,,t j k a a a ，,,s j k a a a 为公差为奇数的等差数列，即得证.（Ⅲ）构造反例：{}n a 为1，2，4，3，6，8，…,2k -1,4k -2,4k ,…,利用反证法，即得证,【详解】（Ⅰ）解：∵a n 12112n n k n n k +=-⎧=⎨-=⎩，，（k ∈N *），∴数列{a n }具有性质P ． 理由如下：当n 为奇数，n ∈N *时，a n ＝n +1包含所有的正偶数， 当n 为偶数，n ∈N *时，a n ＝n ﹣1包含所有的正奇数， ∴无穷数列{a n }的所有项恰好构成全体正整数的一个排列， ∴数列{a n }具有性质P ．（Ⅱ）证明：不妨设1,2,max{,}s t a a m s t === 考虑12,,...,m a a a ，令12max{,,...,}m M a a a =，从1m a +开始寻找第一个大于M 的项，记为：j a ，则12,,...,j a a a 中含有1，2，且j a 为前j 项中的最大项(3j a ≥)(i )若j a 为奇数，22j j a a ->，所以22j a -在j a 之后，记为22k j a a =-，则k j t >>，,,t j k a a a 为公差为奇数的等差数列;(ii ) 若j a 为偶数，令21k j a a =-，则k j s >>，,,s j k a a a 为公差为奇数的等差数列. 故结论成立. （Ⅲ）不一定存在例如{}n a 为1，2，4，3，6，8，…,2k -1,4k -2,4k ,…, 即每三项构成一组，第k 组的通项公式为：2k -1,4k -2,4k ，假设存在4项构成公差为奇数的等差数列，则存在三项（偶数，奇数，偶数）成等差， 由于{}n a 中，任意一项奇数j a 后面的偶数都大于等于2j a ， 因此不可能存在三项（偶数，奇数，偶数）成等差. 故假设不成立.【点睛】本题是数列的创新题型，考查了学生综合分析，转化划归的能力，属于较难题.。

第1页 共16页 第2页 共16页中学生标准学术能力诊断性测试2019年11月测试理科综合试卷（一卷）本试卷共300分，考试时间150分钟。

可能用到的相对原子质量：H 1 O 16 Fe 56 Cu 64 S 32一、选择题：本题共13小题，每小题6分，共78分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．美国免疫学家詹姆斯·艾利森和日本免疫学家本庶佑因发现了用于治疗癌症的免疫调节抑制策略而获得了2018年诺贝尔生理学或医学奖。

他们发现在T 细胞表面有CTLA-4蛋白，在识别目标并接受启动信号时，使T 细胞活性降低，起到免疫刹车作用，从而减弱对癌细胞的攻击，以下理解错误的是A ．CTLA-4的形成需要T 细胞内的核糖体、内质网、高尔基体参与B ．同一个体中的癌细胞与T 细胞的核基因是不同的C ．可通过注射CTLA-4抗体的方式，使癌细胞逃脱免疫系统的监控D ．癌细胞被攻击清除主要依靠细胞免疫产生的效应T 细胞，此过程属于细胞凋亡 2．最新研究发现，“细胞外烟酰胺磷酸核糖转移酶”（eNAMPT ，蛋白质类）不仅能延长小鼠的寿命，还逆转了老鼠身体机能的衰老，这一研究可让人的“返老还童”成为可能。

有关酶的说法错误的是A ．eNAMPT 可与双缩脲试剂反应产生紫色络合物，高温变性后仍能与该试剂变色B ．eNAMPT 可降低反应的活化能，可在最适温度和最适pH 条件下保存C ．eNAMPT 由基因控制合成，影响代谢进而控制生物的性状D ．eNAMPT 的催化具有高效性和专一性，其作用的发挥离不开特定的空间结构3．细胞信号转导是指细胞通过受体感受信息分子的刺激，经胞内信号转导系统转换，从而影响细胞生物学功能的过程。

下图表示两种细胞信号转导形式，有关叙述错误的是A ．甲图的激素可以表示性激素，以自由扩散的方式穿膜，与细胞膜的基本支架有关B ．甲图可说明信息分子可影响基因表达过程，②③的碱基互补配对方式不同C ．甲图中的d 基本骨架为独特的双螺旋结构，e 为mRNA 可作为翻译的模板D ．乙图可以反应细胞膜具有细胞间的信息交流的功能，图中的受体化学本质为糖蛋白4．下表为适宜浓度的α-萘乙酸(NAA)和赤霉素（GA 3）溶液对燕麦胚芽鞘生长的影响，据表分析，下列说法错误的是A B ．若实验用的NAA 浓度为m ，则改用低于m 浓度的NAA 时，胚芽鞘长度不一定减少 C ．NAA 与GA 3可调节植物基因表达，二者混合使用具有协同作用D ．NAA 与GA 3是由植物产生，由产生部位运输到作用部位且具有微量而高效的特点5．将果蝇的一个精原细胞放在3H 标记的胸腺嘧啶脱氧核酸的培养液中培养完成减数分裂产生精子。