理论力学课件
- 格式:doc
- 大小:794.00 KB
- 文档页数:15

1、一点动点:研究对象。
刚体上的点或一个单独的点。
2、二系定系:研究动点运动规律的参考系。
一般取地面。
动系:相对定系运动的参考系。
∞平面。
3、三运动绝对运动(absolute motion):动点相对定系的运动。
即在地面看动点的运动。
相对运动(relative motion):动点相对动系的运动。
即在动系上看动点的运动。
牵连运动(convected motion):动系相对定系的运动。
即在地面上看动系的运动。
动点:P;动系:汽车;定系:地面动点:P;动系:卡盘;定系:地面绝对运动:站在地面看P点直线运动相对运动:站在卡盘上看P点螺旋线牵连运动:站在地面看卡盘的运动定轴转动毛泽东《送瘟神》七律二首一绿水青山枉自多,华佗无奈小虫何!千村薜荔人遗矢,万户萧疏鬼唱歌。
坐地日行八万里,巡天遥看一千河。
牛郎欲问瘟神事,一样悲欢逐逝波。
二春风杨柳万千条,六亿神州尽舜尧。
红雨随心翻作浪,青山着意化为桥。
天连五岭银锄落,地动三河铁臂摇。
借问瘟君欲何在,纸船明烛照天烧。
思考:坐地日行八万里的定系是在那里建立的?地球绕太阳公转的轨迹近似的看作圆,轨道半径万公里4105.1×=R万公里250365/2=Rπ地球的赤道半径公里6400=r万公里01.42=rπ参考系为地心或地轴y 金星如果上帝在创世时与我商量一下,我会给他更好的建议。
选取适当的参考系,可使描述运动的结论:A的常接触点为动点,B为动系。
动点:AB上点A动系:凸轮相对运动轨迹清楚绝对运动:地面上看A 点直线相对运动:凸轮上看A点圆周运动牵连运动:在地面看凸轮的运动定轴转动动点:凸轮上A点动系:顶杆AB相对运动轨迹不清楚1绝对运动:圆周运动牵连运动平移相对运动???动点:OA上的A点动系:BC绝对运动:圆周运动相对运动:直线运动牵连运动:平移相对轨迹清楚动点:O1B上的A点动系:OC绝对运动圆周运动相对运动直线运动牵连运动定轴转动相对轨迹清楚动点:OC上的A点动系:O1B相对轨迹不清楚动点:CD上的B点动系是OA绝对运动相对运动牵连运动直线运动直线运动定轴转动相对轨迹清楚2)无常接触点(线线接触)条件:当两个刚体运动过程中,没有常接触点,只是轮廓线接触.结论:圆心为动点(定系),另一刚体为动系。
7-5 以矢量表示角速度和角加速度·以矢积表示点的速度和加速度一、角速度矢绕定轴转动刚体的角速度可以用矢量表示。
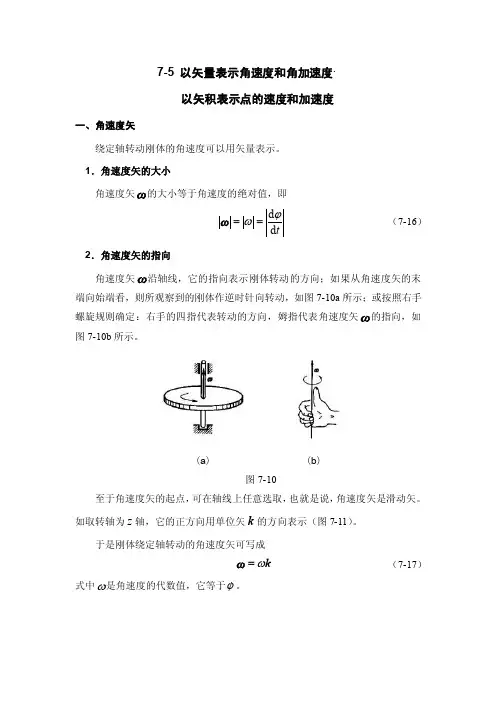
1.角速度矢的大小角速度矢ω的大小等于角速度的绝对值,即td d ϕω==ω (7-16) 2.角速度矢的指向角速度矢ω沿轴线,它的指向表示刚体转动的方向;如果从角速度矢的末端向始端看,则所观察到的刚体作逆时针向转动,如图7-10a 所示;或按照右手螺旋规则确定:右手的四指代表转动的方向,姆指代表角速度矢ω的指向,如图7-10b 所示。
(a ) (b )图7-10至于角速度矢的起点,可在轴线上任意选取,也就是说,角速度矢是滑动矢。
如取转轴为z 轴,它的正方向用单位矢k 的方向表示(图7-11)。
于是刚体绕定轴转动的角速度矢可写成k ω=ω (7-17)式中ω是角速度的代数值,它等于ϕ。
(a ) (b )图7-11二、角加速度矢同样,刚体绕定轴转动的角加速度可以用一个沿坐标轴线的滑动矢量表示:k ε=ε (7-18)式中ε是角加速度的代数值,它等于ω或ϕ 。
于是 )(d dd d k k ωωtt ==ε (7-19)即角加速度ε是角速度矢ω对时间的一阶导数。
根据上述角速度和角加速度的矢量表示法,刚体内任一点的速度可以用矢积 表示。
三、速度的矢量积表示如在轴线上任选一点O 为原点,点M 的矢径以r 表示,如图7-12所示。
图7-12那么,点M 的速度可以用角速度矢与它的矢径的矢量积来表示,即r v ⨯=ω (7-20)为了证明这一点,需证明矢积r ⨯ω确实表示点M 的大小和方向。
根据矢积的定义知,r ⨯ω仍是一个矢量,它的大小是v r r =⋅=⋅=⨯R ωωωθsin式中θ是角速度矢ω与矢径r 的夹角。
于是证明了矢积r ⨯ω的大小等于速度的大小。
矢积r ⨯ω的方向垂直于ω和r 所组成的平面(即图7-12中三角形OMO 1平面),从矢量v 的末端向始端看,则见ω按逆时针转向转过角θ与r 重合,由图容易看出,矢积r ⨯ω的方向正好与点M 的方向相同。

理论力学Theoretical Mechanics综合实验楼504 yliu5@要求•上课认真听讲,作笔记,积极思考•及时完成作业考核平时+研究性学习报告+期末绪论1.关于力学2.力学的发展简史3.力学的学科性质4.力学的研究方法5.力学的学科分类6.关于理论力学第1章静力学基本概念§1-1 刚体和力的概念§1-2 静力学公理§1-3 力的解析表示吊车梁的弯曲变形一般不超过跨度(A、B间距离)的1/500,水平方向变形更小。
因此,研究吊车梁的平衡规律时,变形是次要因素,可略去不计。
实际物体受力时,其内部各点间的相对距离都要发生改变,其结果是使物体的形状和尺寸改变,这种改变称为变形(deformation)。
物体变形很小时,变形对物体的运动和平衡的影响甚微,因而在研究力的作用效应时,可以忽略不计,这时的物体便可抽象为刚体(rigid body)。
如果变形体在某一力系作用下已处于平衡,则将此变形体刚化为刚体时,其平衡不变,这一论断称为刚化原理(rigidity principle)。
当研究航天器轨道问题时——质点当研究航天器姿态问题时——刚体、质点系、刚体系2.力的概念力(Force)是物体间相互的机械作用力对物体产生的效应一般可分为两个方面:一是物体运动状态的改变,另一个是物体形状的改变。
通常把前者称为力的运动效应(effect of motion),后者称为力的变形效应(effect of deformation)。
理论力学中把物体都视为刚体,因而只研究力的运动效应,即研究力使刚体的移动或转动状态发生改变这两方面的效应。
来表示,如图。
物体受力一般是通过物体间直接或间接接触进行的。
接触处多数情况下不是一个点,而是具有一定尺寸的面积。
因此无论是施力体还是受力体,其接触处所受的力都是作用在接触面积上的分布力(distributed force)。
当分布力作用面积很小时,为了分析计算方便起见,可以将分布力简化为作用于一点的合力,称为集中力(concentrated force)。








第三章 力系的平衡方程及其应用3-3在图示刚架中,已知kN/m 3=m q ,26=F kN ,m kN 10⋅=M ,不计刚架自重。
求固定端A 处的约束力。
032242234,0022,0022,01)(1i =∙-∙+--==-==-+=∑∑∑F F F M M MF F Fiy F F F FA FA AY AX x解得m kN 12kN 60⋅===A Ay Ax M F F ,,3-4杆AB 及其两端滚子的整体重心在G 点,滚子搁置在倾斜的光滑刚性平面上,如图所示。
对于给定的θ角,试求平衡时的β角。
B解:解法一:AB 为三力汇交平衡,如图所示ΔAOG 中βs i nl AO =, θ-︒=∠90AOG ,β-︒=∠90OAG ,βθ+=∠AGO 由正弦定理:)90sin(3)sin(sin θβθβ-︒=+l l ,)cos 31)sin(sin θβθβ=+l 即 βθβθθβs i n c o s c o s s i n c o s s i n3+= 即 θβt a n t a n2= )t a n 21a r c t a n(θβ= 解法二::0=∑x F ,0sin R =-θG F A(1)第三章 力系的平衡方程及其应用0=∑y F ,0cos R =-θG F B(2)0)(=∑F A M ,0sin )sin(3R =++-ββθl F lG B (3)解(1)、(2)、(3)联立,得 )t a n 21a r c t a n (θβ=3-5 由AC 和CD 构成的组合梁通过铰链C 连接。
支承和受力如图所示。
已知均布载荷强度kN/m 10=q ,力偶矩m kN 40⋅=M ,不计梁重。
解:取CD 段为研究对象,受力如图所示。
0)(=∑F CM,024=--q M F D ;kN 15=D F取图整体为研究对象,受力如图所示。
0)(=∑F AM ,01682=--+q M F F D B;kN 40=B F 0=∑yF ,04=+-+D BAyF q F F ;kN 15-=Ay F0=∑x F ,0=AxF解得kN 15kN 5kN 40kN 15===-=D C B A F F F F ;;;3-6如图所示,组合梁由AC 和DC 两段铰接构成,起重机放在梁上。
已知起重机重P1 = 50kN ,重心在铅直线EC 上,起重载荷P2 = 10kN 。
如不计梁重,求支座A 、B 和D 三处的约束反力。
解:(1)取起重机为研究对象,受力如图。
0)(=∑F F M ,0512P R =--W F F G ,kN 50R =G F(2)取CD 为研究对象,受力如图0)(=∑F C M ,016'R R =-G D F F ,kN 33.8R =D F(3)整体作研究对象,受力图(c )0)(=∑F A M ,0361012R P R =+--B D F F W F ,kN 100R =B F0=∑x F ,0=Ax F0=∑y F ,kN 33.48-=Ay F3-7 构架由杆AB ,AC 和DF 铰接而成,如图所示。
在DEF 杆上作用一矩为M 的力偶。
不计各杆的重量,求AB 杆上铰链A ,D 和B 所受的力。
解 对整体(图(a )),有∑∑=--===02,0)00M aF F M F X By CBx(,解得 aM F F By Bx 2,0-== 再研究DEF 杆(图(b )),有∑∑∑=++==++==+=0,00,002,0)(AyDyByAxDxBxDxBxAF F F Y F F F X aF aF F M 解得 aM F F F Ay Dx Ax 2,0-===3-8 图示构架中,物体P 重1200N ,由细绳跨过滑轮E 而水平系于墙上,尺寸如图。
不计杆和滑轮的重量,求支承A 和B 处的约束力,以及杆BC 的内力F BC 。
解:(1)整体为研究对象,受力图(a ),W F =T0=∑A M ,0)5.1()2(4T R =--+-⋅r F r W F B ,N 1050R =B F0=∑x F ,N 1200T ===W F F Ax 0=∑y F ,N 501=Ay F(2)研究对象CDE (BC 为二力杆),受力图(b )0=∑D M ,0)5.1(5.1sin T =-+⋅+⨯r F r W F BC θN 1500541200sin -=-=-=θW F BC (压力)3-9 图示结构中,A 处为固定端约束,C 处为光滑接触,D 处为铰链连接。
已知N 40021==F F ,m N 300⋅=M ,mm 400==BC AB ,mm 300==CE CD ,︒=45α,不计各构件自重,求固定端A处与铰链D处 的约束力。
解 先研究DCE 杆,如图(a ),由,0)(,00011x =∙--∙==-+===∑∑∑DE F M CD FF M F FF Y F X NcDDy NcD ,解得 N F N F F NC D y D x 1800,1400,0=-==再研究ABC 杆,如图(b ),由45sin ,0)(045sin ,0045cos 0222=∙++︒∙==-︒-==︒-=∑∑∑AB F MAC F F M F F F Y F F X ANCANCAyAx,解得 m N M N F N F A Ay Ax ∙-===1178,2083,22003-10 图示结构由直角弯杆DAB 与直杆BC 、CD 铰接而成,并在A 处与B 处用固定铰支座和可动铰支座固定。
杆DC 受均布载荷q 的作用,杆BC 受矩为2qa M =的力偶作用。
不计各构件的自重。
求铰链D 受的力。
解先研究BC杆,受力如图(b),由0=-=∑MaFFMCxB,)(得qaFCx=CD杆受力如图(a),由∑∑=-==+=2,0)(xDyCCxDaFaqaFMFFX,解得qaFqaFqaFDDyDx25,21,==-=3-11 图示构架,由直杆BC,CD及直角弯杆AB组成,各杆自重不计,载荷分布及尺寸如图。
在销钉B上作用载荷P。
已知q、a、M、且2qaM=。
求固定端A的约束力及销钉B对BC 杆、AB杆的作用力。
解 先研究CD 杆如图(b ),由02a 0=-=∑aqa F F M Cx D ,)( 解得 qa F Cx 21=研究BC 杆(包括销钉B ),受力如图(d ),由∑∑∑=∙-+-==-==-∙+=03213,0)(0003210y x x aa q aF aF M F M F F Y F a q F X BAxBAy A A BAy A BA A ,,解得A 处约束反力a qa P M qa P F qa F A Ay Ax )(,,+=+=-=研究销钉B 如图(e ),图中x BC F 、BCy F 是BC 杆对销钉B 的作用力,000=-+==+=∑∑P F FY F F X BCy BAyBCx BAx,解得 qa F qa F BCy BCx -=-=,213-12无重曲杆ABCD 有两个直角,且平面ABC 与平面BCD 垂直。
杆的D 端为球铰支座,A 端为轴承约束,如图所示。
在曲杆的AB 、BC 和CD 上作用三个力偶,力偶所在平面分别垂直于AB 、BC 和CD 三线段。
已知力偶矩M 2和M 3 ,求使曲杆处于平衡的力偶矩M 1和D A 、处的约束力。
解:如图所示:∑==0,0D x xF F∑=0yM ,012=⋅-d F M Az ,12d M F Az=∑=0z F ,12d M F Dz -= ∑=0zM,013=⋅+d F M Ay ,13d M F Ay-= ∑=0yF13d M F Dy =∑=0x M 0231=⋅+⋅--d F d F M Az Ay ,2123131M d dM d d M +=3-13在图示转轴中,已知:Q=4KN ,r=0.5m ,轮C 与水平轴AB 垂直,自重均不计。
试求平衡时力偶矩M 的大小及轴承A 、B 的约束反力。
解:m KN M Qr M M y∙==-=∑2,0,00,0==∑AYN Y026,0=∙-∙=∑Q N M BzxKN N BZ 34=∑==0,0BXzN M 0,0==∑AX N XKN N Q N N Z AZ BzAZ38,0,0==-+=∑3-14匀质杆AB 重Q 长L ,AB 两端分别支于光滑的墙面及水平地板上,位置如图所示,并以二水平索AC 及BD 维持其平衡。
试求(1)墙及地板的反力;(2)两索的拉力。
解:Q NZ B==∑0∑=0XM06030sin 2130sin =︒∙-︒∙-︒∙BDtg S BD Q BD N c B Q S C 144.0=∑=0YM06060sin 2160sin =︒∙+︒∙+︒∙-BDtg N BD Q BD N A B Q N A 039.0=0=∑Y 060cos =+︒-C BS SQ S B 288.0=3-14 平面悬臂桁架所受的载荷如图所示。
求杆1,2和3的内力。
解 用截面法取分离如图(b ),由4222,0)(0642,0)211=--+-∙-==---∙-=∑∑F F F F CD F F M F F F AB F F M CA (解得 F F F F 2,333.521=-=再研究节点B ,受力如图(c )由,0sin 032=-+=∑F F FY θ,得F F 667.13-=3-15 平面桁架的支座和载荷如图所示。
ABC 为等边三角形,E ,F 为两腰中点,又AD=DB 。
求杆CD 的内力CD F 。
ED 为零杆,取BDF 研究,F CD =-0.866F3-16 桁架受力如图所示,已知kN 101=F ,kN 2032==F F 。
试求桁架4,5,7,10各杆的内力。
解 先研究整体如图(a ),由2.14260sin 5,0)(060sin ,0060cos 0321213x=---︒==︒+--==+︒-=∑∑∑aF aFaF aF F M F F F F Y F F F X BABAyBA ,解得KNF KN F KN F Ay Ay B 197.568.5,64.28=-==再用截面法取分离体如图(b ),由cos ,00sin ,002.1,0)(87676=+++==+==-∙-=∑∑∑F F F F X F F Y aF F a F M AxAyAyEθθ解得KNF KN F KN F 35.14771.6,33.4876=-=-=最后研究节点G ,如图(c ),由0,00019810=-==-=∑∑F F Y F F X ,解得 KN F KN F 35.14,10109==3-17 平面桁架的支座和载荷如图所示,求杆1,2和3的内力。