2018年丰台二模数学文科

丰台区2018—2019学年度第二学期综合练习（二）高三数学（文科） 2019.05一、选择题（共8小题，每小题5分，共40分）二、填空题（共6小题，每小题5分，共30分。

有两空的小题，第一空3分，第二空2分）9．3π10．35 11．412．满足12,0a a >,0d <(答案不唯一) 13．( 14．6； 三、解答题（共6小题，共80分） 15．（共13分）解：（Ⅰ）因为11a =，1e n n a a +=⋅()n *∈N ，所以数列{}n a 是1为首项，e 为公比的等比数列，所以1n n a e -=. ………………4分 （Ⅱ）由（Ⅰ）知，1ln ln e 1n n a n -==-， ………………5分所以 (1)012(1)2n n n T n -=++++-=， ………………7分 所以23111nT T T +++2222122334(1)n n =++++⨯⨯⨯-11111112[(1)()()()]223341n n =-+-+-++-- ………………10分 12(1)n =-.………………11分 因为10n >，所以111n -<.所以12(1)2n -<即231112nT T T +++< ………………13分16．（共13分）解:（Ⅰ）由已知)(x f 图象得 2.A =3342T π=，则 2T =π. 因为22T ωπ==π，0ω> 所以1ω=. …………2分 因为02ϕπ<<， 所以3ϕπ=. …………4分 所以()2sin(+)3f x x π=． …………6分（Ⅱ）由题可得：()2cos2g x x =． …………8分故()2sin 2y g x x =+2cos22sin2x x =++)4x π=． …………10分因为3+22+2242k x k ππππ+π≤≤， …………11分所以5++88k x k ππππ≤≤. 所以()g x 的单调递减区间为5+,+,88k k k ππ⎡⎤ππ∈⎢⎥⎣⎦Z . …………13分17．（共13分） 解：（Ⅰ）高一年级知识竞赛的达标率为10.0350.85-⨯=. ………………4分（Ⅱ）高一年级成绩为[95,100]的有0.025404⨯⨯=名，记为1A ，2A ，3A ，4A ，高二年级成绩为[95,100]的有2名，记为1B ，2B . ………………6分 选取2名学生的所有可能为：12A A ，13A A ，14A A ，11A B ，12A B ，23A A ，24A A ，21A B ，22A B ，34A A ，31A B ，32A B ，41A B ，42A B ，12B B ，共15种；其中2名学生来自于同一年级的有12A A ，13A A ，14A A ，23A A ，24A A ，34A A ，12B B ，共7种； ………………8分 设2名学生来自于同一年级为事件A ， 所7()15P A =. ………………10分（Ⅲ）12X X <． ………………13分18．（共14分）解：（Ⅰ）证明：因为在菱形ABCD 中，3ADC π∠=，O 为线段CD 的中点， 所以'OD AO ⊥． ………………1分因为平面⊥'AOD 平面ABCO ， 平面 'AOD 平面AO ABCO =，'OD ⊂平面'AOD ，所以'OD ⊥平面ABCO ． ………………4分 因为BC ⊂平面ABCO ，所以'OD BC ⊥． ………………5分（Ⅱ）证明：如图，取P 为线段'AD 的中点，连接OP ，PM ；因为在'ABD ∆中，P ，M 分别是线段'AD ，'BD 的中点，所以AB PM //，AB PM 21=． 因为O 是线段CD 的中点，菱形ABCD 中，AB DC a ==，DC AB //，所以122aOC CD ==．所以AB OC //，AB OC 21=． ………………6分 所以OC PM //，OC PM =．所以四边形OCMP 为平行四边形， ………………7分 所以OP CM //，因为⊄CM 平面'AOD ，⊂OP 平面'AOD ，所以//CM 平面'AOD ； ………………10分（Ⅲ）解：由（Ⅰ）知'OD ⊥平面ABCO ．所以'OD 是四棱锥'D ABCO -的高． ………………11分因为1'3V S OD =⨯⨯==底，所以2a =． ………………14分解：（Ⅰ）由题知22224,1,2.a c a abc =⎧⎪⎪=⎨⎪⎪=+⎩解得2,a b =⎧⎪⎨=⎪⎩ …………………3分 所以求椭圆E 的方程为22143x y +=．…………………5分 （Ⅱ）由（Ⅰ）知()2,0A -,()2,0B当直线l 的斜率不存在时，直线l 的方程为1x =．由221 1.43x x y=⎧⎪⎨+=⎪⎩，解得1,3.2x y =⎧⎪⎨=⎪⎩或1,3.2x y =⎧⎪⎨=-⎪⎩ 得1213,22k k ==或1213,22k k =-=-；均有1213k k =． 猜测存在13λ=．…………………6分当直线l 的斜率存在时，设直线l 的方程为()1y k x =-，()11,C x y ，()22,D x y ．由()2211.43y k x x y =-⎧⎪⎨+=⎪⎩，得()22224384120k x k x k +-+-=．则212221228,43412.43k x x k k x x k ⎧+=⎪⎪+⎨-⎪=⎪+⎩…………………8分故1212121323(2)y y k k x x -=-+-…………………9分2112123(2)(2)3(2)(2)x y x y x x --+=+-()1212122583(2)(2)k x x x x x x -++⎡⎤⎣⎦=+- 2222128(3)40843433(2)(2)k k k k k x x ⎡⎤--+⎢⎥++⎣⎦=+- 0.= …………………13分所以存在常数13λ=使得1213k k =恒成立 …………………14分解：（Ⅰ）当3a =时， 32()3f x x x =-，2'()363(2)f x x x x x =-=-． …………………2分当[0,2]x ∈时，'()0f x ≤，所以()f x 在区间[0,2]上单调递减． …………………4分 所以()f x 在区间[0,2]上的最小值为(2)4f =-． …………………5分（Ⅱ）设过点(1,(1))P f 的曲线()y f x =的切线切点为00(,)x y ，2'()32f x x ax =-，(1)1f a =-， 所以320002000,(1)(32)(1).y x ax y a x ax x ⎧=-⎪⎨--=--⎪⎩ 所以320002(3)210x a x ax a -+++-=．令32()2(3)21g x x a x ax a =-+++-， 则2()62(3)2g x x a x a '=-++(1)(62)x x a =--，令()0g x '=得1x =或3a x =， 因为3a >，所以1a>． ()g x 的极小值为()(1)03ag g <=，所以()g x 在(,)3a-∞上有且只有一个零点1x =．因为3222()2(3)21(1)(1)0g a a a a a a a a =-+++-=-+>，所以()g x 在(,)3a+∞上有且只有一个零点．所以()g x 在R 上有且只有两个零点．即方程320002(3)210x a x ax a -+++-=有且只有两个不相等实根，所以过点(1,(1))P f 恰有2条直线与曲线()y f x =相切． …………………13分（若用其他方法解题，请酌情给分）。

适用精选文件资料分享2018 年丰台区初三数学二模试题（有答案）丰台区 2018 年初三一致练习（二）数学试卷2018. 05考生须知 1. 本试卷共 8 页，共三道大题， 28 道小题，满分 100 分。

考试时间120 分钟。

2. 在试卷和答题卡上仔细填写学校名称、姓名和考号。

3.试题答案一律填涂或书写在答题卡上，在试卷上作答无效。

4.在答题卡上，选择题、作图题用 2B 铅笔作答，其余试题用黑色笔迹署名笔作答。

5. 考试结束，将本试卷、答题卡一并交回。

一、选择题（本题共 16 分，每题 2 分）第 1-8 题均有四个选项，吻合题意的选项只有一个． 1 ．南水北调工程在保障城市供水安全、增添国都水资源战略贮备、改进居民生活用水条件、促进水资源涵养和恢复等方面，获得了重要的社会、经济、生态等综合效益 . 自 2008年 9月至 2018 年 5 月，北京已累计收水超出 5 000 000 000 立方米 .将 5000 000 000 用科学记数法表示为（A）（B）（C）（D） 2 ．为丰富公民精神文化生活，提高文化涵养，全国各地陆续睁开全民阅读活动 . 此刻的图书室不但是人们学习知识的地方，更是成为人们休闲的好去处 . 以下图书室标记的图形中不是轴对称图形的是（A）（B）（C）（D）我厉害了的国3 ．如图是一个小正方体的睁开图，把睁开图折叠成小正方体后，有“我”字一面的相对面上的字是（A）厉（B）害（C）了（D）国 4 ．实数 a，b，c 在数轴上的对应点的地点以以下图，假如 a + b = 0 ，那么以下结论正确的是（A）（B）（C）（D） 5 ．如图是小明利用等腰直角三角板丈量旗杆高度的表示图 . 等腰直角三角板的斜边 BD与地面 AF平行，当小明的视野恰好沿 BC经过旗杆顶部点 E 时，丈量出此时他所在的地点点 A与旗杆底部点 F 的距离为米.假如小明的眼睛距离地面米，那么旗杆 EF的高度为（A）米（B）米（C）米（D）米 6 ．已知，则代数式的值为（A）3 （B）1（C）-1 （D）-3 7．为适应新中考英语听闻机考，九年级甲、乙两位同学使用某手机软件进行英语听闻练习并记录了 40 次的练习成绩 .甲、乙两位同学的练习成绩统计结果以以下图：甲同学的练习成绩统计图乙同学的练习成绩统计图以下说法正确的选项是（A）甲同学的练习成绩的中位数是38 分（B）乙同学的练习成绩的众数是15 分（C）甲同学的练习成绩比乙同学的练习成绩更稳固（D）甲同学的练习总成绩比乙同学的练习总成绩低 8 ．某挪动通信公司有两种挪动电话计费方式，这两种计费方式中月使用费 y（元）与主叫时间 x（分）的对应关系以以下图：（主叫时间不到 1 分钟，按 1 分钟收费）以下三个判断中正确的选项是①方式一每个月主叫时间为 300 分钟时，月使用费为 88 元②每个月主叫时间为350 分钟和 600分钟时，两种方式收费同样③每个月主叫时间超出 600分钟，选择方式一更省钱（A）①② （B）①③ （C）②③ （D）①②③二、填空题（本题共16 分，每题 2 分） 9 ．分解因式： a3 - ab2= ． 10 ．正六边形每个内角的度数是．11．假如关于x的不等式ax > 2 的解集为 x <，写出一个满足条件的 a = ． 12 ．一个盒子里装有除颜色外都同样的10 个球，此中有 a 个红球， b 个黄球， c 个白球 .从盒子里随意摸出 1 个球，摸出黄球的概率是，那么 a =，b = ，c = ．（写出一种状况即可） 13 ．“中兴号”是我国拥有完好自主知识产权、达到世界先进水平的动车组列车 . “中兴号”的速度比本来列车的速度每小时快 50 千米，加速后从北京到上海运转时间缩短了 30 分钟 . 已知从北京到上海全程约 1320 千米，求“中兴号”的速度 . 设“中兴号”的速度为千米 / 时，依题意，可列方程为__________________．14．如图，在平面直角坐标系 xOy中，正方形 OABC的边长为 1，点 D，E分别在 OA，OC上， OD = CE，△ OCD可以看作是△ CBE经过若干次图形的变化（平移、轴对称、旋转）获取的，写出一种由△ CBE获取△OCD的过程：．15．如图，是一辆小汽车与墙平行停放的平面表示图，汽车靠墙一侧OB与墙 MN平行且距离为 0.8 米，一辆小汽车车门宽 AO为 1.2 米，当车门打开角度∠ AOB为 40°时，车门能否会碰到墙？；（填“是”或“否”）请简述你的原由．（参照数据： sin40 °≈ 0.64 ，cos40°≈ 0.77 ，tan40 °≈ 0.84 ）16．数学课上，老师提出以下问题：△ABC是⊙O的内接三角形，OD⊥BC 于点 D.请借助直尺，画出△ ABC中∠ BAC的均分线 . 晓龙同学的画图步骤以下：（1）延长 OD交于点 M；（2）连接 AM交 BC于点 N. 所以线段 AN为所求△ ABC中∠ BAC的均分线 . 请回答：晓龙同学画图的依照是 . 三、解答题（本题共 68 分，第 17-22 ，24 题每题 5 分，第 23，25 题每题 6 分，第 26-28 题每题 7 分） 17 ．计算：．18．解分式方程：.19．如图， E，C 是线段 BF 上的两点， BE = FC，AB∥DE，∠ A=∠D，AC=6，求 DF的长 .20．在平面直角坐标系xOy 中，已知抛物线y = x2 - 4x + 2m - 1与 x 轴交于点 A，B. （点 A 在点 B 的左边）（1）求 m的取值范围；（2）当 m取最大整数时，求点 A、点 B 的坐标．21．如图， BD是△ ABC的角均分线，过点 D作 DE∥BC交 AB于点 E，DF∥AB交 BC于点 F．（1）求证：四边形 BEDF为菱形；（2）假如∠A = 90 °，∠ C = 30 °， BD = 12，求菱形 BEDF的面积．22．在平面直角坐标系 xOy 中，直线 l ： . （1）判断直线 l 能否经过点M（2，1），并说明原由；（2）直线l 与反比率函数的图象的交点分别为点 M，N，当 OM=ON时，直接写出点 N的坐标 .23．某校七年级 6 个班的 180 名学生马上参加北京市中学生开放性科学实践活动送课到校课程的学习.学习内容包含以下7 个领域： A.自然与环境， B. 健康与安全， C.结构与机械， D.电子与控制， E. 数据与信息，F. 能源与资料，G.人文与历史 .为认识学生喜爱的课程领域，学生会睁开了一次检查研究，请将下边的过程补全.采集数据学生会计划检查 30 名学生喜爱的课程领域作为样本，下边抽样检查的对象选择合理的是 ___________；（填序号）① 选择七年级1班、2班各 15 名学生作为检核对象②选择机器人社团的 30 名学生作为检核对象③选择各班学号为6 的倍数的30 名学生作为检核对象检核对象确立后，检查小组获取了 30 名学生喜爱的课程领域以下： A ，C，D，D，G，G，F，E，B，G， C，C，G，D，B，A，G，F，F，A，G，B，F，G，E，G，A，B，G，G 整理、描述数据整理、描述样本数据，绘制统计图表以下，请补全统计表和统计图．某校七年级学生喜爱的课程领域统计表某校七年级学生喜爱的课程领域统计图课程领域人数A4B4C3D3E2FG合计30分析数据、推测结论请你依据上述果向学校介绍本次送到校的程域，你的介绍是__________（填 A-G 的字母代号），估整年大有 _________名学生喜个程域．24．如，⊙O中，AB是⊙O的直径，G弦AE的中点，接OG并延交⊙O 于点 D，接 BD交 AE于点 F，延 AE至点 C，使得 FC = BC，接 BC. （1）求：BC是⊙O的切；（2）⊙O的半径 5，，求 FD的．25．数学活上，老提出：如，有一 4dm， 3dm的方形板，在板的四个角裁去四个同样的小正方形，而后把四折起来，做成一个无盖的盒子，小正方形的多少，盒子的体最大 . 下边是研究程，充完好：（1）小正方形的 x dm，体 y dm3，依据方体的体公式获取 y 和 x 的关系式：；（2）确立自量 x 的取范是；（3）列出 y 与 x 的几 .x/dm ⋯ 1 ⋯ y/dm3 ⋯⋯（明：表格中相关数保留一位小数）（4）在下边的平面直角坐系中，描出以全后的表中各坐的点，画出函数的象；（5）合画出的函数象，解决：当小正方形的 dm ，盒子的体最大，最大 dm3.26．在平面直角坐系 xOy中，二次函数的象的点点 D．（1）当，求点 D 的坐；（2）当≤ ≤，求函数的最小 m．（用含 h 的代数式表示 m） 27 ．如，正方形 ABCD中，点 E 是 BC上的一个点，接 AE，将段 AE点 A 逆旋 90°，获取 AF，接 EF，交角 BD于点 G，接 AG．（1）依据意全形；（2）判断 AG与 EF 的地点关系并明；（3）当 AB= 3，BE= 2 ，求段 BG 的．28．在平面直角坐系 xOy中，将随意两点与之的“直距”定： . 比方：点 M （1，），点 N（3，）， . 已知点 A(1，0) 、点 B(-1 ，4). （1），；（2）假如直AB上存在点C，使得2，你求出点C的坐；（3）假如⊙B的半径3，点E ⊙B上一点，你直接写出的取范 .丰台区 2018 年初三第二次一初三数学参照答案一、（本共 16分，每小 2分）号 12345678答案CBDCB D A A 二、填空（本共 16 分，每小 2 分） 9 ．； 10 ．120°；11．-1（答案不独一）； 12 ．2，5，3（答案不独一）； 13 ．； 14 ．将△CBE点 C逆旋90°，再向下平移 1 个位获取△ OCD（答案不独一）； 15 ．否，求出点 A 与直 OB的距离 d1，通算可得 d1 <0.8 ，因此不会碰到； 16 ．垂径定理，等弧所的周角相等．三、解答（本共 68 分，第 17―22、24 ，每小5 分；第 23，256 分；第 26，27，28 ，每小7 分）17．解：．= ⋯⋯⋯⋯⋯⋯⋯⋯4分 = . ⋯⋯⋯⋯⋯⋯⋯⋯5分 18 ．解：去分母，得 x2-x （x-2 ）=x- 2⋯⋯⋯⋯⋯⋯⋯⋯2分解个方程，得 x=- 2 ⋯⋯⋯⋯⋯⋯⋯⋯4分 x=-2 是原方程的解．∴原方程的解是 x=-2 ．⋯⋯⋯5分19．明：∵AB∥DE，∴∠ ABC=∠DEF. ⋯⋯⋯⋯⋯⋯⋯⋯⋯1分∵BE=FC，∴BE +EC=FC+EC，∴BC=EF．⋯⋯⋯⋯⋯⋯⋯⋯⋯2分又∵∠ A=∠D，∴△ ABC≌△ DEF，⋯⋯⋯⋯⋯⋯⋯⋯⋯3分∴AC=DF．⋯⋯⋯⋯⋯⋯⋯⋯⋯4分又∵AC=6，∴DF=6．⋯⋯⋯⋯⋯⋯⋯⋯⋯5分 20 ．解：（1）∵抛物y=x2-4x+2m-1 与 x 有两个交点，令 y=0. ∴x2-4x+2m-1=0. ∵与 x 有两个交点，∴方程有两个不等的数根 . ∴Δ>0. 即=(-4)2- 4?(2m- 1)>0∴m<2.5.⋯⋯⋯⋯⋯⋯⋯⋯⋯2 分（2）∵，且 m取最大整数，∴m=2. ⋯⋯⋯⋯⋯⋯⋯⋯⋯3分当 m=2 ，抛物 y=x2-4x+2m-1= x2-4x+3. 令 y=0，得 x2-4x+3=0，解得 x1 = 1，x2=3. ∴抛物与x 两个交点的坐 A（1，0），B（3，0）. ⋯⋯⋯⋯⋯5分21．（1）明：∵ DE∥BC，DF∥AB，∴四形 BEDF平行四形⋯⋯⋯⋯⋯⋯1 分∴∠ 1=∠3. ∵BD是△ ABC的角均分，∴∠ 1=∠2.∴∠ 2=∠3. ∴BF=DF. ∴四形 BEDF菱形. ⋯⋯⋯⋯⋯⋯⋯⋯⋯2分（2）解：点D作DG⊥BC于点G，∠BGD=90°. ∵∠ A=90°，∠ C=30°，∴∠ ABC=60°. 由（ 1）知，BF=DF，∠ 2=30°， DF∥AB，∴∠ DFG=∠ABC=60°. ∵BD=12，∴在Rt△BDG中， DG=6. ∴在 Rt△FDG中， DF= . ⋯⋯⋯⋯⋯⋯⋯⋯⋯4分∴BF= DF= . ∴S菱形 BEDF . ⋯⋯⋯⋯⋯⋯⋯⋯⋯5分（其余法相分）22 ．（1）解：直 l 点 M（2，1）. ⋯⋯ . ⋯⋯ . ⋯⋯ . ⋯⋯1分原由以下：于，令x=2，∴直l 点 M（2，1）. . ⋯⋯ . ⋯⋯ . ⋯⋯2分（2）点 N的坐（1，2），（-2 ，-1 ），（-1 ，-2 ）. . ⋯⋯ . ⋯⋯ . ⋯⋯5分 23 ．采集数据抽象合理的是③ . ⋯⋯⋯⋯⋯⋯⋯⋯⋯1分整理、描述数据以下：⋯⋯⋯⋯⋯⋯⋯⋯⋯4 分某校七年学生喜的程域表某校七年学生喜的程域程域人数F 4 G 10 分析数据、推测 G，60.⋯⋯⋯⋯⋯⋯⋯⋯⋯6分 24 ．（1）明：∵G 弦 AE的中点，∴ OD⊥AE. ⋯⋯ . ⋯⋯ . ⋯⋯⋯⋯⋯1分∴∠ DGC=90°. ∴∠ D +∠DFG=90°. ∵FC=BC，∴∠ 1＝∠ 2. ∵∠ DFG =∠1，∴∠DFG＝∠ 2. ∵OD=OB，∴∠ D＝∠ 3. ∴∠ 3 + ∠2=90°. ∴∠ ABC＝90°. 即 CB⊥AB. ∴BC是⊙O的切. ⋯⋯ . ⋯⋯ . ⋯⋯⋯⋯⋯2分（2）解：∵ OA=5，tanA= ，∴在Rt△AGO中，∠AGO＝90°，OG=3，AG=4. ∵OD=5，∴DG=2. ∵AB=2OA=10，∴在Rt△ABC中，∠ ABC＝90°， BC= ，AC= . ∴FC=BC= . ∴ . ∴在Rt△DGF中，FD=. ⋯5分（其余法或解法相分. ）25 ．解：（1） . ⋯⋯1分（2）0<x<1.5.⋯⋯⋯⋯⋯⋯⋯⋯⋯2 分（3）如下表，⋯⋯⋯⋯⋯⋯⋯⋯⋯4 分（4）如右；⋯⋯⋯⋯⋯⋯⋯⋯⋯5分（ 5）至均可， 3.0 至 3.1 均可⋯⋯⋯⋯⋯⋯⋯⋯⋯6 分26．解：（1）∵抛物 = （x-h ）2+h-h2，∴ 点 D的坐（ h， h-h2 ），∴当h=-1 ，点 D 的坐是（-1 ，-2 ）．⋯⋯⋯⋯3分（2）当 x=-1 ，y= 3h+1，当 x=1 ，y=-h+1 ．⋯⋯⋯⋯4分①当 h<-1，函数的最小 m= 3h+1 ⋯⋯⋯⋯5分②当- 1≤h≤1 ，，函数的最小 m= h-h2 ⋯⋯⋯⋯6分③当 h>1 ，，函数的最小 m=-h+1 ⋯⋯⋯⋯7分27．解：（1）形全后如⋯⋯⋯⋯⋯⋯⋯1 分（2）：AG⊥EF．⋯⋯⋯⋯⋯⋯⋯2分明：接FD， F 点 FM∥BC，交BD的延于点 M．∵四形 ABCD是正方形，∴AB=DA=DC=BC，∠DAB=∠ABE=∠ADC=90°，∠ADB=∠5=45°．∵ 段 AE点 A 逆旋 90°，获取 AF，∴AE=AF，∠FAE=90°．∴∠ 1=∠2．∴△ FDA≌△ EBA．⋯⋯⋯⋯⋯⋯⋯3分∴∠FDA=∠EBA=90°，FD=BE．∵∠ ADC=90°，∴∠ FDA+∠ADC=180°。

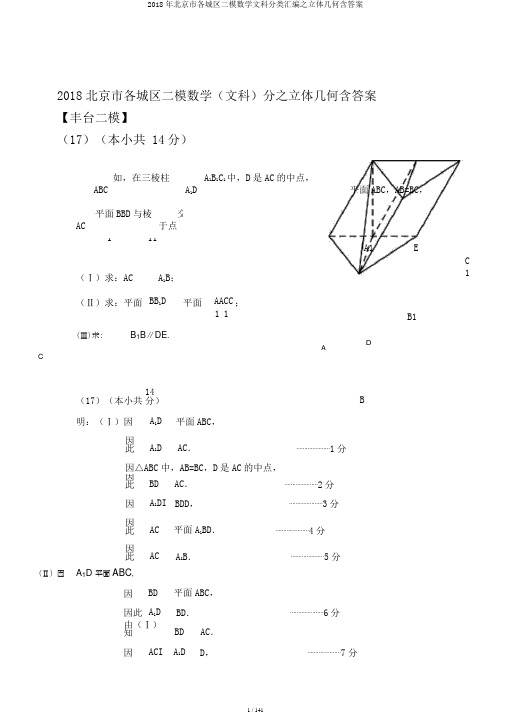
2018北京市各城区二模数学（文科）分之立体几何含答案【丰台二模】（17）（本小共14分）如，在三棱柱ABCA1B1C1中，D是AC的中点，A1D平面ABC，AB=BC，平面BBD与棱AC交于点111A1E（Ⅰ）求：AC A1B；C 1（Ⅱ）求：平面BB1D平面AACC；11B1（Ⅲ）求：B1B∥DE．ADC（17）（本小共14分）B明：（Ⅰ）因A1D平面ABC，因此A1D AC．⋯⋯⋯⋯⋯⋯⋯1分因△ABC中，AB=BC，D是AC的中点，因此BD AC．⋯⋯⋯⋯⋯⋯⋯2分因A1DI BDD，⋯⋯⋯⋯⋯⋯⋯3分因此AC平面A1BD．⋯⋯⋯⋯⋯⋯⋯4分因此AC A1B．⋯⋯⋯⋯⋯⋯⋯5分（Ⅱ）因A1D平面ABC，因BD平面ABC，因此A1D BD．⋯⋯⋯⋯⋯⋯⋯6分由（Ⅰ）知BD AC．因ACI A1D D，⋯⋯⋯⋯⋯⋯⋯7分因此BD平面A1ACC1．⋯⋯⋯⋯⋯⋯⋯8分因BD平面BB1D，因此平面BB1D平面AAC11C．⋯⋯⋯⋯⋯⋯⋯9分（Ⅲ）因在三棱柱ABC A1B1C1中，面A1ABB1平行四形，因此B1B∥A1A．⋯⋯⋯⋯⋯⋯⋯10分因B1B平面A1ACC1，A1A平面A1ACC1，⋯⋯⋯⋯⋯⋯⋯11分因此B1B∥平面A1ACC1．⋯⋯⋯⋯⋯⋯⋯12分因B1B平面BB1D，且平面BB1DI平面A1ACC1DE，⋯⋯⋯13分因此B1B∥DE．⋯⋯⋯⋯⋯⋯⋯14分【旭日二模】18.（本小题满分13分）如图,在四棱锥P ABCD中,!PBC是等腰三角形,且PBPC 3.四边形ABCD是直角梯形,AB//DC,ADDC,AB5,AD4,DC3.（Ⅰ）求证:AB//平面PDC;（Ⅱ）当平面PBC平面ABCD时,求四棱锥P ABCD的体积;（Ⅲ）请在图中所给的五个点P,A,B,C,D中找出两个点,使得这两点所在的直线与直线BC垂直,并给出证明.．．分析:（Ⅰ）由于AB//CD,CD平面PDC,AB平面PDC因此AB//平面PDC（Ⅱ）在梯形ABCD中,过点C作CF AB于F,取CD中点E,连结PE,由于PC PB因此在!PCB中,PE BC,由于面PBC面ABCD,面PBCI面ABCD=BC因此PE面ABCD由于AB//CD，AD CD,CF AB,AB 5,AD 4,DC 3因此CF 4,BF 222,在!CFB中,BCCF BF25PEPE2CE22由于S梯形ABCD(AB DC)162132因此VPABCD3S梯形ABCDPE3取BC的中点E,连结PE由于PB PC,因此PB BC,则PE3252由于平面PBC平面ABCD,平面PBCI平面ABCD BC,PB BC因此PB平面ABCD则四棱锥P ABCD的体积为:S1(35)4232323（Ⅲ）点P和点A,连结AC和AE则AC32425AB,AE均分BC,因此AE BCPD CEA B又PE BC,PE平面PAE,AE平面PAE,AEIPE E因此BC平面PAE,PA平面PAE,因此BC PA即证点P和点A所在的直线PA与直线BC垂直.【东城二模】（18）（本小题14分）如图，在三棱柱ABC A1B1C1中，侧棱垂直于底面，ACBC，AC BCCC1，E，F分别为A1B1，BC的中点．（Ⅰ）求证：AC C1F；C1B1（Ⅱ）求证：BE∥平面AC11F；EA1（Ⅲ）在棱CC1上能否存在一点G，使得平面B1EG平面AC11F？说明原因．FCB （18）（共14分）A解：（Ⅰ）在三棱柱ABCA1B1C1中，由于侧棱垂直于底面，因此CC1平面ABC．因此CC1AC．由于AC BC，CC1IBC C，因此AC平面BCC1B1．由于C1F平面BCC1B1，因此AC C1F．5分（Ⅱ）取A1C1中点H，连结EH，FH．则EH∥B1C1，且EH 1B1C1，H 2A1又由于BF∥B1C1，且BF 1B1C1，2因此EH∥BF，且EH BF．因此四边形BEHF为平行四边形．因此BE∥FH．A又BE平面AC11F，FH平面AC11F，因此BE∥平面ACF．1 1（Ⅲ）在棱CC1上存在点G，且G为CC1的中点．连结EG,GB1．C1在正方形BB1C1C中，由于F为BC中点，A1因此△B1C1G≌△C1CF．G因此C1CF B1GC190．C因此B1G C1F．由（Ⅰ）可得AC平面BB1C1C，A由于AC//A1C1，因此A1C1平面BB1C1C．由于B1G平面BB1C1C，因此AC11B1G．由于1111，AC ICF C因此B1G平面AC11F．由于B1G平面B1EG，因此平面B1EG平面AC11F．C1B1ECF B10分B1EFB14分【西城二模】（18．（本小分14分）如，梯形ABCD所在的平面与等腰梯形ABEF所在的平面相互垂直，AB//CD//EF，AB AD，G AB的中点．CD DA AF FE2，AB4．（Ⅰ）求：DF//平面（Ⅱ）求：平面BCF（Ⅲ）求多面体AFEBCD BCE；平面GCE；的体．18．（本小分14分）解：（Ⅰ）因CD//EF，且CD EF，因此四形CDFE平行四形，因此DF//CE．⋯⋯2分因DF平面BCE，⋯⋯3分因此DF//平面BCE．⋯⋯4分（Ⅱ）接FG．因平面ABCD平面ABEF，平面ABCDI平面ABEF AB，AD AB，因此AD平面ABEF，因此BF AD．⋯⋯⋯⋯⋯⋯6分因G AB的中点，因此AG//CD，且AG CD；EF//BG，且EF BG，因此四形AGCD和四形BEFG均平行四形．因此AD//CG，因此BFCG．⋯⋯⋯⋯⋯⋯7分因EFEB，因此四形BEFG菱形，因此BF EG．⋯⋯⋯⋯⋯⋯8分因此BF平面GCE．⋯⋯⋯⋯⋯⋯9分因此平面BCF平面GCE．⋯⋯⋯⋯⋯⋯10分（Ⅲ）BFIGE O．由（Ⅰ）得DF//CE，因此DF//平面GCE，由（Ⅱ）得AD//CG，因此AD//平面GCE，因此平面ADF//平面GCE，因此几何体ADF GCE是三棱柱．⋯⋯⋯⋯⋯⋯11分由（Ⅱ）得BF平面GCE．因此多面体AFEBCD的体V V ADFGCE V BGCE⋯⋯⋯⋯⋯⋯12分S GCE1S GCE BO FO34S GCE FO 83．⋯⋯⋯⋯⋯⋯14分33【海淀二模】（17）（本小题14分）如图，已知菱形AECD的对角线AC,DE交于点F，点E为的AB中点.将三角形ADE沿线段DE折起到PDE的地点，如图2所示.（Ⅰ）求证：DE平面PCF；；（Ⅱ）证明：平面PBC平面PCF；（Ⅲ）在线段PD,BC上能否分别存在点M,N，使得平面CFM//平面PEN？若存在，请指出点M,N的地点，并证明；若不存在，请说明原因.17．（本小14分）（Ⅰ）明：折叠前，因四形AECD菱形，因此AC DE；因此折叠后，DE PF,DE CF,又PFICF F,PF,CF平面PCF，因此DE平面PCF⋯⋯⋯⋯⋯⋯⋯4 分（Ⅱ）因四形AECD菱形，因此DC//AE,DC AE.又点E AB的中点，因此DC//EB,DC EB.因此四形DEBC平行四形.因此CB//DE.又由（Ⅰ）得，DE平面PCF,因此因CB 平面PCF. CB 平面PBC，因此平面PBC平面PCF.⋯⋯⋯⋯⋯⋯⋯9分（Ⅲ）存在知足条件的点M,N,且M,N分别是PD和BC的中点.如图，分别取PD和BC的中点M,N.连结EN,PN,MF,CM.由于四边形DEBC为平行四边形，1因此EF//CN,EF BC CN.2因此四边形ENCF为平行四边形.因此FC//EN.在PDE中，M,F分别为PD,DE中点，因此MF//PE.又EN,PE平面PEN,PEIEN E,MF,CF平面CFM,因此平面CFM//平面PEN.【昌平二模】18.（本小题14分）如图，四边形ABCD是正方形，平面ABCD平面ABEF，AF//BE,AB BE,ABBE2,AF1．（Ⅰ）求证：AC平面BDE；14分EF（Ⅱ）求证：AC//平面DEF；（III）求三棱锥D-FEB的体积.18.（共14分）A B OD C证明：（I）由于正方形ABCD,因此AC BD.又由于平面ABEF平面ABCD,平面ABEF I平面ABCD=AB,AB BE,BE平面ABEF,因此BE平面ABCD.又由于AC平面ABCD.故BE AC.又由于BEIBDB，因此AC平面BDE.--------------------5分（II）取DE的中点G，连结OG,FG，由于四边形ABCD为正方形，因此O为BD的中点．则OG//BE，且OG1BE．2由已知AF//BE，且AF1BE，则AF//OG且AFOG，2EFGA B因此四边形AOGF为平行四边形，因此AO//FG，O 即AC//FG．由于AC平面DEF，FG平面DEF，因此AC//平面DEF．--------------------10分D C（III）由于平面 ABCD平面ABEF，四边形ABCD是正方形，平面ABEF I平面ABCD=AB,因此AD//BC,AD AB.由（I）知，BE平面ABCD，AD平面ABCD因此BE AD因此AD平面BEF.因此V DBEF1S BEF AD11BE ABAD 4.--------------------14分3323【顺义二模】（本小题满分13分）如图,直三棱柱ABC A1B1C1的侧棱长为1,AB AC 1,BC2,D是BC的中点..（Ⅰ）求证:AD平面B1BCC1;（Ⅱ）求证:A1B//平面ADC1;（Ⅲ）求三棱锥B1ADC1的体积.【房山二模】（18）（本小题14分）如图1，正六边形ABCDEF的边长为2，O为中心，G为AB的中点.现将四边形DEFC沿CF折起到四边形D1E1FC的地点，使得平面ABCF平面D1E1FC，如图2.（Ⅰ）证明：D1F平面E1OG；（Ⅱ）求几何体E1-OFAG的体积；（Ⅲ）在直线AB上能否存在点H，使得D1H//平面E1OG？假如存在，求出AH的长；假如不E D存在，请说明原因.F.OC A G BE1D1F COCF （18）（Ⅰ）证明:图（1）中OG图（2）中，OG CFA G B又面CD1E1F面ABCF，面CD1E1FI面ABCF=CFOG面CD1E1FQD1F面CD1E1FOGD1F又O为CF的中点OF//D1E1，又E1D1E1F四边形E1D1OF为菱形=D1F OE1QOGIOE1=O D1F面E1OG5分E1D1（Ⅱ）图二中，过E1作E1M FO，垂足为MFO CQOG面CD1E1F，E1M面CD1E1FE1MOG MQOGIFOO E1M面AGOF E1M为E1-OFAG的AG B高，E1M=2sin603S四OFAG=(1+2)31=33V 1Sh310分2232（Ⅲ）过C作CH AB,交AB的延伸线于点HCH//OG又OE1//CD1,CD1I CH C面D1CH//面E1OGHD1H//面E1OGQD1H面D1CHQ四形OGHC矩形GH=CO=2AH=3⋯⋯⋯⋯14分。

北京市丰台区2018年高三二模数学(文科)试卷及答案丰台区2018年高三年级第二学期综合练习（二） 2018.5高三数学（文科）第一部分 （选择题 共40分）一、选择题共8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一项。

（1）已知U =R ，2{|230}A x xx =--<，则UA =ð(A) {|1x x ≤-或3}x ≥ (B) {|3x x ≤-或1}x ≥ (C) {|1x x <-或3}x > (D) {|3x x <-或1}x >（2）设a ，b 为非零向量，则“∥a b ”是“a 与b 方向相同”的(A) 充分而不必要条件 (B) 必要而不充分条件(C) 充分必要条件 (D) 既不充分也不必要条件（3）设双曲线2221(0)x y a a-=>的一条渐近线的倾斜角为π6，则a = (A) 3(B) 23(C)(D)（4）某四棱锥的三视图如图所示，则该四棱锥的俯视图侧视图正视图体积为 (A) 1 (B) 2 (C) 3(D) 6（5）下列函数中，既是偶函数，又在区间)0,(-∞上为减函数的是 (A)2log ()y x =-(B) xx y -=1(C)21y x =-+ (D) ||e x y =（6）执行如图所示的程序框图，则输出的S 值为 (A) 25 (B)20(C) 13(D) 6（7）在△ABC 中，D 为AB 中点，E 为CD 中点，设AB =a ，AC =b，若AE λμ=+a b ，则λμ的值是(A) 14(B) 12(C) 2(D) 4（8）某游戏开始时，有红色精灵m 个，蓝色精灵n个．游戏规则是：任意点击两个精灵，若两精灵同色，则合并成一个红色精灵，若两精灵异色，则合并成一个蓝色精灵，当只剩一个精灵时，游戏结束．那么游戏结束时，剩下的精灵的颜色(A) 只与m 的奇偶性有关 (B) 只与n 的奇偶性有关 (C) 与m ，n 的奇偶性都有关 (D) 与m ，n 的奇偶性都无关第二部分 （非选择题 共110分）二、填空题共6小题，每小题5分，共30分。

丰台区2018年初三统一练习（二）数 学 试 卷2018. 05考生须知 1. 本试卷共8页，共三道大题，28道小题，满分100分。

考试时间120分钟。

2. 在试卷和答题卡上认真填写学校名称、姓名和考号。

3. 试题答案一律填涂或书写在答题卡上，在试卷上作答无效。

4. 在答题卡上，选择题、作图题用2B 铅笔作答，其他试题用黑色字迹签字笔作答。

5. 考试结束，将本试卷、答题卡一并交回。

一、选择题（本题共16分，每小题2分）第1-8题均有四个选项，符合题意的选项只有．．一个． 1．南水北调工程在保障城市供水安全、增加首都水资源战略储备、改善居民生活用水条件、促进水资源涵养和恢复等方面，取得了重大的社会、经济、生态等综合效益. 自2008年9月至2018年5月，北京已累计收水超过5 000 000 000立方米.将5 000 000 000用科学记数法表示为 （A ）100.510⨯（B ）10510⨯（C ）9510⨯（D ）85010⨯2．为丰富国民精神文化生活，提升文化素养，全国各地陆续开展全民阅读活动. 现在的图书馆不单是人们学习知识的地方，更是成为人们休闲的好去处. 下列图书馆标志的图形中不．是．轴对称图形的是（A ） （B ） （C ） （D ）3．如图是一个小正方体的展开图，把展开图折叠成小正方体后，有“我”字一面的相对面上的字是 （A ）厉 （B ）害 （C ）了（D ）国4．实数a ，b ，c 在数轴上的对应点的位置如图所示，如果a + b = 0，那么下列结论正确的是 （A ）>a c（B ）0a c +<（C ）0abc <（D ）0ab=5．如图是小明利用等腰直角三角板测量旗杆高度的示意图. 等腰直角三角板的斜边BD 与地面AF 平行，当小明的视线恰好沿BC 经过旗杆顶部点E 时，测量出此时他所在的位置点A 与旗杆底部点F 的距离为10米. 如果小明的眼睛距离地面1.7米，那么旗杆EF 的高度为 （A ）10米 （B ）11.7米 （C ）102米（D ）(52 1.7)+米6．已知111m n-=，则代数式222m mn n m mn n --+-的值为（A ）3（B ）1（C ）-1 （D ）-37．为适应新中考英语听说机考，九年级甲、乙两位同学使用某手机软件进行英语听说练习并记录了40次的练习成绩. 甲、乙两位同学的练习成绩统计结果如图所示：甲同学的练习成绩统计图 乙同学的练习成绩统计图下列说法正确的是（A ）甲同学的练习成绩的中位数是38分 （B ）乙同学的练习成绩的众数是15分（C ）甲同学的练习成绩比乙同学的练习成绩更稳定 （D ）甲同学的练习总成绩比乙同学的练习总成绩低8．某移动通讯公司有两种移动电话计费方式，这两种计费方式中月使用费y （元）与主叫时间x （分）的对应关系如图所示：（主叫时间不到1分钟，按1分钟收费）下列三个判断中正确的是① 方式一每月主叫时间为300分钟时，月使用费为88元 ② 每月主叫时间为350分钟和600分钟时，两种方式收费相同 ③ 每月主叫时间超过600分钟，我厉 害 了 的国abcFABCDEy /元方式二方式一60088O200138400x /分58O。

丰台区2018年初三统一练习(二）数 学 试 卷2018. 05考生须知 1。

本试卷共8页，共三道大题，28道小题，满分100分。

考试时间120分钟。

2. 在试卷和答题卡上认真填写学校名称、姓名和考号。

3. 试题答案一律填涂或书写在答题卡上，在试卷上作答无效。

4. 在答题卡上，选择题、作图题用2B 铅笔作答,其他试题用黑色字迹签字笔作答.5。

考试结束，将本试卷、答题卡一并交回.一、选择题（本题共16分，每小题2分）第1-8题均有四个选项,符合题意的选项只有．．一个． 1．南水北调工程在保障城市供水安全、增加首都水资源战略储备、改善居民生活用水条件、促进水资源涵养和恢复等方面，取得了重大的社会、经济、生态等综合效益. 自2008年9月至2018年5月，北京已累计收水超过5 000 000 000立方米.将5 000 000 000用科学记数法表示为 （A ）100.510⨯（B ）10510⨯（C ）9510⨯（D ）85010⨯2．为丰富国民精神文化生活，提升文化素养，全国各地陆续开展全民阅读活动. 现在的图书馆不单是人们学习知识的地方，更是成为人们休闲的好去处。

下列图书馆标志的图形中不．是．轴对称图形的是（A) （B ） （C ） (D ）我3．如图是一个小正方体的展开图，把展开图折叠成小正方体后，有“我”字一面的相对面上的字是 （A)厉 （B)害 (C ）了（D ）国4．实数a ，b ,c 在数轴上的对应点的位置如图所示，如果a + b = 0，那么下列结论正确的是（A ）>a c (B ）0a c +< (C ）0abc <（D ）0a b=5．如图是小明利用等腰直角三角板测量旗杆高度的示意图。

等腰直角三角板的斜边BD 与地面AF 平行，当小明的视线恰好沿BC 经过旗杆顶部点E 时,测量出此时他所在的位置点A 与旗杆底部点F 的距离为10米. 如果小明的眼睛距离地面1.7米,那么旗杆EF 的高度为 （A ）10米（B)11.7米(C ）102米 （D ）(52 1.7)+米 6．已知111m n-=,则代数式222m mn n m mn n --+-的值为 （A ）3（B ）1 （C ）—1（D ）—37．为适应新中考英语听说机考，九年级甲、乙两位同学使用某手机软件进行英语听说练习并记录了40次的练习成绩. 甲、乙两位同学的练习成绩统计结果如图所示：甲同学的练习成绩统计图 乙同学的练习成绩统计图厉 害 了 的国abcFAB C DE下列说法正确的是（A)甲同学的练习成绩的中位数是38分 （B ）乙同学的练习成绩的众数是15分(C ）甲同学的练习成绩比乙同学的练习成绩更稳定 （D ）甲同学的练习总成绩比乙同学的练习总成绩低8．某移动通讯公司有两种移动电话计费方式，这两种计费方式中月使用费y （元）与主叫时间x （分）的对应关系如图所示：(主叫时间不到1分钟，按1分钟收费）下列三个判断中正确的是① 方式一每月主叫时间为300分钟时，月使用费为88元 ② 每月主叫时间为350分钟和600分钟时，两种方式收费相同 ③ 每月主叫时间超过600分钟,选择方式一更省钱 （A ）①② （B ）①③ （C)②③ （D ）①②③ 二、填空题(本题共16分，每小题2分) 9．分解因式:a 3 — ab 2 = ． 10．正六边形每个内角的度数是 ．11．如果关于x 的不等式ax > 2的解集为x <2a,写出一个满足条件的a = ．12．一个盒子里装有除颜色外都相同的10个球，其中有a 个红球，b 个黄球,c 个白球. 从盒子里随意摸出1个球，摸出黄球的概率是12，那么 a = ，b = ，c = ．(写出一种情况即可）13．“复兴号”是我国具有完全自主知识产权、达到世界先进水平的动车组列车。

2018年北京市丰台区高考数学二模试卷（文科）一、选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1．（5分）已知U＝R，A＝{x|x2﹣2x﹣3＜0}，则∁U A＝（）A．{x|x≤﹣1或x≥3}B．{x|x≤﹣3或x≥1}C．{x|x＜﹣1或x＞3}D．{x|x＜﹣3或x＞1}2．（5分）设，为非零向量，则“”是“与方向相同”的（）A．充分而不必要条件B．必要而不充分条件C．充分必要条件D．既不充分也不必要条件3．（5分）设双曲线的一条渐近线的倾斜角为，则a＝（）A．B．C．D．4．（5分）某四棱锥的三视图如图所示，则该四棱锥的体积为（）A．1B．2C．3D．65．（5分）下列函数中，既是偶函数，又在区间（﹣∞，0）上为减函数的是（）A．y＝log2（﹣x）B．C．y＝﹣x2+1D．y＝e|x|6．（5分）执行如图所示的程序框图，则输出的S值为（）A．25B．20C．13D．67．（5分）在△ABC中，D为AB中点，E为CD中点，设＝，＝，若＝λ+μ，则的值是（）A．B．C．2D．48．（5分）某游戏开始时，有红色精灵m个，蓝色精灵n个．游戏规则是：任意点击两个精灵，若两精灵同色，则合并成一个红色精灵，若两精灵异色，则合并成一个蓝色精灵，当只剩一个精灵时，游戏结束．那么游戏结束时，剩下的精灵的颜色（）A．只与m的奇偶性有关B．只与n的奇偶性有关C．与m，n的奇偶性都有关D．与m，n的奇偶性都无关二、填空题共6小题，每小题5分，共30分．9．（5分）复数的虚部为．10．（5分）已知实数x，y满足不等式组，则x+4y的最大值是．11．（5分）已知圆C：（x﹣1）2+y2＝4，则过点P（2，）且与圆C相切的直线方程为．12．（5分）已知函数y＝sin（ωx+φ）（ω＞0，）的部分图象如图所示，则ω＝；φ＝．13．（5分）设函数①f（2）＝；②若f（x+1）＞1，则x的取值范围是．14．（5分）如图，在矩形ABCD中，AB＝4，AD＝2，E为AB的中点．将△ADE 沿DE翻折，得到四棱锥A1﹣DEBC．设A1C的中点为M，在翻折过程中，有下列三个命题：①总有BM∥平面A1DE；②线段BM的长为定值；③存在某个位置，使DE与A1C所成的角为90°．其中正确的命题是．（写出所有正确命题的序号）三、解答题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．15．（13分）如图所示，在△ABC中，D是BC边上一点，AB＝14，BD＝6，AD ＝10，．（Ⅰ）求∠ADB；（Ⅱ）求AC的长．16．（13分）已知数列{a n}的前n项和，等比数列{b n}满足a1＝3b1，b2b4＝a2．（Ⅰ）求数列{a n}的通项公式；}的前n项和T n．（Ⅱ）求数列{b2n﹣117．（14分）如图，在三棱柱ABC﹣A1B1C1中，D是AC的中点，A1D⊥平面ABC，AB＝BC，平面BB1D与棱A1C1交于点E．（Ⅰ）求证：AC⊥A1B；（Ⅱ）求证：平面BB1D⊥平面AA1C1C；（Ⅲ）求证：B1B∥DE．18．（13分）某汽车生产厂家为了解某型号电动汽车的“实际平均续航里程数”，收集了使用该型号电动汽车1年以上的部分客户的数据，得到他们的电动汽车的“实际平均续航里程数”．从年龄在40岁以下的客户中抽取8位归为A 组，从年龄在40岁（含40岁）以上的客户中抽取8位归为B组，将他们的电动汽车的“实际平均续航里程数”整理成如下茎叶图：注：“实际平均续航里程数”是指电动汽车的行驶总里程与充电次数的比值．（Ⅰ）分别求出A组客户与B组客户“实际平均续航里程数”的平均值；（Ⅱ）在A，B两组客户中，从“实际平均续航里程数”大于335的客户中各随机抽取1位客户，求A组客户的“实际平均续航里程数”不小于B组客户的“实际平均续航里程数”的概率；（Ⅲ）试比较A，B两组客户数据方差的大小．（结论不要求证明）19．（13分）已知函数f（x）＝（x﹣a）cos x﹣sin x，x∈（0，π），（a∈R）．（Ⅰ）求f（x）的单调区间；（Ⅱ）若对于任意x1∈（0，π），存在x2∈（0，π），都有，求a的取值范围．20．（14分）已知椭圆C：的长轴长为4，离心率为，过右焦点的直线l与椭圆相交于M，N两点，点P的坐标为（4，3），记直线PM，PN的斜率分别为k1，k2．（Ⅰ）求椭圆C的方程；（Ⅱ）当时，求直线l的斜率；（Ⅲ）求证：k1+k2为定值．2018年北京市丰台区高考数学二模试卷（文科）参考答案与试题解析一、选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1．（5分）已知U＝R，A＝{x|x2﹣2x﹣3＜0}，则∁U A＝（）A．{x|x≤﹣1或x≥3}B．{x|x≤﹣3或x≥1}C．{x|x＜﹣1或x＞3}D．{x|x＜﹣3或x＞1}【解答】解：A＝{x|﹣1＜x＜3}；∴∁U A＝{x|x≤﹣1，或x≥3}．故选：A．2．（5分）设，为非零向量，则“”是“与方向相同”的（）A．充分而不必要条件B．必要而不充分条件C．充分必要条件D．既不充分也不必要条件【解答】解：对于非零向量，，由⇒与方向相同或相反，反之，与方向相同⇒，则“”是“与方向相同”的必要而不充分条件．故选：B．3．（5分）设双曲线的一条渐近线的倾斜角为，则a＝（）A．B．C．D．【解答】解：双曲线的一条渐近线方程y＝x，由题意可得＝tan＝，∴a＝，故选：C．4．（5分）某四棱锥的三视图如图所示，则该四棱锥的体积为（）A．1B．2C．3D．6【解答】解：由三视图还原原几何体如图，可知该几何体为四棱锥，底面ABCD为直角梯形，∠ABC＝90°，AB∥CD，AB＝2，CD＝1，P A⊥底面ABCD，P A＝2．∴该四棱锥的体积为．故选：A．5．（5分）下列函数中，既是偶函数，又在区间（﹣∞，0）上为减函数的是（）A．y＝log2（﹣x）B．C．y＝﹣x2+1D．y＝e|x|【解答】解：对于A，由﹣x＞0，得x＜0，函数的定义域为（﹣∞，0），函数为非奇非偶函数；对于B，y＝的定义域为{x|x≠1}，函数为非奇非偶函数；对于C，y＝﹣x2+1的定义域为R，在（﹣∞，0）上为增函数；对于D，y＝e|x|，定义域为R，且f（﹣x）＝f（x），函数为偶函数，∵内函数t＝|x|在（﹣∞，0）上为减函数，而外函数为增函数，由复合函数的单调性可得，y＝e|x|在（﹣∞，0）上为减函数．故选：D．6．（5分）执行如图所示的程序框图，则输出的S值为（）A．25B．20C．13D．6【解答】解：第一次执行循环体后，S＝2，k＝2，不满足退出循环的条件；第二次执行循环体后，S＝6，k＝3，不满足退出循环的条件；第三次执行循环体后，S＝13，k＝4，满足退出循环的条件；故输出的S＝13，故选：C．7．（5分）在△ABC中，D为AB中点，E为CD中点，设＝，＝，若＝λ+μ，则的值是（）A．B．C．2D．4【解答】解：∵D为AB中点，E为CD中点，∴＝+＝+＝，∴λ＝，μ＝，∴＝．故选：B．8．（5分）某游戏开始时，有红色精灵m个，蓝色精灵n个．游戏规则是：任意点击两个精灵，若两精灵同色，则合并成一个红色精灵，若两精灵异色，则合并成一个蓝色精灵，当只剩一个精灵时，游戏结束．那么游戏结束时，剩下的精灵的颜色（）A．只与m的奇偶性有关B．只与n的奇偶性有关C．与m，n的奇偶性都有关D．与m，n的奇偶性都无关【解答】解：每碰一次，就少一个精灵，所以当最后只剩一个精灵时，碰了m+n ﹣1次，任意两个精灵相碰，有三种情况：第一种情况：红色+红色→红色，此时红色精灵减少1个，蓝色精灵数量不变；第二种情况：蓝色+蓝色→红色，此时红色精灵增加1个，蓝色精灵减少2个；第三种情况：红色+蓝色→蓝色，此时红色精灵减少1个，蓝色精灵数量不变；根据以上分析可知，每碰一次，蓝色精灵的数量要么不变，要么减少2，也就是说，每碰一次蓝色精灵数量的奇偶性不变．开始时，蓝色精灵有n个，当n是奇数时，最后剩下的只能是一个蓝色精灵；当n是偶数时，最后剩下的只能是一个红色精灵．∴游戏结束时，剩下的精灵的颜色只与n的奇偶性有关．故选：B．二、填空题共6小题，每小题5分，共30分．9．（5分）复数的虚部为．【解答】解：复数＝＝＝﹣i的虚部为﹣．故答案为：﹣．10．（5分）已知实数x，y满足不等式组，则x+4y的最大值是5．【解答】解：由实数x，y满足不等式组作出可行域如图，联立，解得A（1，1），化目标函数z＝x+4y，由图可知，当直线z＝x+4y过A时，直线在y轴上的截距最大，z有最大值为1+4＝5．故答案为：5．11．（5分）已知圆C：（x﹣1）2+y2＝4，则过点P（2，）且与圆C相切的直线方程为．【解答】解：由已知得，点P（2，）在圆C：（x﹣1）2+y2＝4上，∵，∴过点P（2，）且与圆C相切的直线的斜率为﹣，则切线方程为y﹣，即．故答案为：．12．（5分）已知函数y＝sin（ωx+φ）（ω＞0，）的部分图象如图所示，则ω＝2；φ＝．【解答】解：根据函数y＝sin（ωx+φ）（ω＞0，）的部分图象，可得A＝1，•＝﹣，∴ω＝2．再根据五点法作图可得2×+φ＝，∴φ＝，故答案为：2；．13．（5分）设函数①f（2）＝﹣1；②若f（x+1）＞1，则x的取值范围是．【解答】解：①∵函数∴f（2）＝＝﹣1②若x+1≤0，则f（x+1）＞1可化为：﹣（x+1）﹣2＞1，解得：x＜﹣4；若x+1＞0，则f（x+1）＞1可化为：＞1，解得：﹣1＜x＜﹣；故x的取值范围是：，故答案为：﹣1，14．（5分）如图，在矩形ABCD中，AB＝4，AD＝2，E为AB的中点．将△ADE 沿DE翻折，得到四棱锥A1﹣DEBC．设A1C的中点为M，在翻折过程中，有下列三个命题：①总有BM∥平面A1DE；②线段BM的长为定值；③存在某个位置，使DE与A1C所成的角为90°．其中正确的命题是①②．（写出所有正确命题的序号）【解答】解：取A1D的中点N，连接MN，EN，则MN为△A1CD的中位线，∴MN CD，又BE为矩形ABCD的边AB的中点，∴BE CD，∴MN BE，即四边形MNEB为平行四边形，∴BM∥EN，又EN⊂平面A1DE，BM⊄平面A1DE，∴BM∥平面A1DE，故①正确；由四边形MNEB为平行四边形可得BM＝NE，而在翻折过程中，NE的长度保持不变，故BM的长为定值，故②正确；取DE的中点O，连接A1O，CO，由A1D＝A1E可知A1O⊥DE，若DE⊥A1C，则DE⊥平面A1OC，∴DE⊥OC，又∠CDO＝90°﹣∠ADE＝45°，∴△OCD为等腰直角三角形，故而CD＝OD，而OD＝DE＝，CD＝4，与CD＝OD矛盾，故DE与A1C所成的角不可能为90°．故③错误．故答案为：①②．三、解答题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．15．（13分）如图所示，在△ABC中，D是BC边上一点，AB＝14，BD＝6，AD ＝10，．（Ⅰ）求∠ADB；（Ⅱ）求AC的长．【解答】（本小题共13分）解：（Ⅰ）在△ADB中，由余弦定理得＝＝．…………………（2分）因为∠ADB∈（0，π），…………………（3分）所以．…………………（5分）（Ⅱ）由，可知，…………………（6分）所以…………………（8分）＝．…………………（10分）在△ADC中，由正弦定理得，…………………（12分）所以，所以．…………………（13分）16．（13分）已知数列{a n}的前n项和，等比数列{b n}满足a1＝3b1，b2b4＝a2．（Ⅰ）求数列{a n}的通项公式；}的前n项和T n．（Ⅱ）求数列{b2n﹣1【解答】解：（Ⅰ）因为，所以a1＝S1＝3．…………………（1分）＝3n2﹣3（n﹣1）2＝6n﹣当n≥2时，a n＝S n﹣S n﹣13．…………………（3分）因为当n＝1时，6×1﹣3＝3＝a1，…………………（4分）所以数列{a n}的通项公式是a n＝6n﹣3．…………………（5分）（Ⅱ）设数列{b n}的公比为q．因为a1＝3b1，所以b1＝1．…………………（6分）因为b2•b4＝a2，所以．…………………（8分）因为，所以b3＝3，且q2＝3．…………………（10分）因为{b n}是等比数列，}是首项为b1＝1，公比为q2＝3的等比数列．…………………所以{b2n﹣1（11分）所以．即．…………………（13分）17．（14分）如图，在三棱柱ABC﹣A1B1C1中，D是AC的中点，A1D⊥平面ABC，AB＝BC，平面BB1D与棱A1C1交于点E．（Ⅰ）求证：AC⊥A1B；（Ⅱ）求证：平面BB1D⊥平面AA1C1C；（Ⅲ）求证：B1B∥DE．【解答】（本小题共14分）证明：（Ⅰ）因为A1D⊥平面ABC，所以A1D⊥AC．…………………（1分）因为△ABC中，AB＝BC，D是AC的中点，所以BD⊥AC．…………………（2分）因为A1D∩BD＝D，…………………（3分）所以AC⊥平面A1BD．…………………（4分）所以AC⊥A1B．…………………（5分）（Ⅱ）因为A1D⊥平面ABC，因为BD⊂平面ABC，所以A1D⊥BD．…………………（6分）由（Ⅰ）知BD⊥AC．因为AC∩A1D＝D，…………………（7分）所以BD⊥平面A1ACC1．…………………（8分）因为BD⊂平面BB1D，所以平面BB1D⊥平面AA1C1C．…………………（9分）（Ⅲ）因为在三棱柱ABC﹣A1B1C1中，侧面A1ABB1为平行四边形，所以B1B∥A1A．…………………（10分）因为B1B⊄平面A1ACC1，A1A⊂平面A1ACC1，…………………（11分）所以B1B∥平面A1ACC1．…………………（12分）因为B1B⊂平面BB1D，且平面BB1D∩平面A1ACC1＝DE，…………………（13分）所以B1B∥DE．…………………（14分）18．（13分）某汽车生产厂家为了解某型号电动汽车的“实际平均续航里程数”，收集了使用该型号电动汽车1年以上的部分客户的数据，得到他们的电动汽车的“实际平均续航里程数”．从年龄在40岁以下的客户中抽取8位归为A 组，从年龄在40岁（含40岁）以上的客户中抽取8位归为B组，将他们的电动汽车的“实际平均续航里程数”整理成如下茎叶图：注：“实际平均续航里程数”是指电动汽车的行驶总里程与充电次数的比值．（Ⅰ）分别求出A组客户与B组客户“实际平均续航里程数”的平均值；（Ⅱ）在A，B两组客户中，从“实际平均续航里程数”大于335的客户中各随机抽取1位客户，求A组客户的“实际平均续航里程数”不小于B组客户的“实际平均续航里程数”的概率；（Ⅲ）试比较A，B两组客户数据方差的大小．（结论不要求证明）【解答】（本小题共13分）解：（Ⅰ）A组平均值为：；……………（1分）B组平均值为：．……………（2分）（Ⅱ）将A组客户中实际平均续航里程数为338，340的客户分别记为a1，a2；将B组客户中实际平均续航里程数为338，340，360，380的客户分别记为b1，b2，b3，b4．从A，B两组实际平均续航里程数大于335km的客户中各随机抽取1位客户的事件包括：a1b1，a1b2，a1b3，a1b4，a2b1，a2b2，a2b3，a2b4，共8种，…………………（5分）其中A组客户的实际平均续航里程数不小于B组客户的实际平均续航里程数的事件包括：a1b1，a2b1，a2b2，共3种．…………………（7分）设“A组客户的实际平均续航里程数不小于B组客户的实际平均续航里程数”为事件M，…………………（8分）则．…………………（10分）所以A组客户的实际平均续航里程数不小于B组客户的实际平均续航里程数的概率为．（III）A组数据的方差小于B组数据的方差．…………………（13分）19．（13分）已知函数f（x）＝（x﹣a）cos x﹣sin x，x∈（0，π），（a∈R）．（Ⅰ）求f（x）的单调区间；（Ⅱ）若对于任意x1∈（0，π），存在x2∈（0，π），都有，求a的取值范围．【解答】解：（Ⅰ）根据题意，f（x）＝（x﹣a）cos x﹣sin x，则f'（x）＝﹣（x ﹣a）sin x．因为x∈（0，π），所以sin x＞0．由f'（x）＝0得x＝a．当a≤0时，f'（x）＜0，f（x）在（0，π）上单调递减；当a≥π时，f'（x）＞0，f（x）在（0，π）上单调递增；当0＜a＜π时，x，f'（x），f（x）的变化情况如下表：所以f（x）的单调递增区间是（0，a），单调递减区间是（a，π）．综上所述，当a≤0时，f（x）在（0，π）上单调递减；当a≥π时，f（x）在（0，π）上单调递增；当0＜a＜π时，以f（x）的单调递增区间是（0，a），单调递减区间是（a，π）．（Ⅱ）设g（x）＝x2﹣2x﹣1．因为g（x）＝（x﹣1）2﹣2，当x＝1时，g（x）有最小值为﹣2．因为对于任意x1∈（0，π），存在x2∈（0，π），都有，所以，即．所以π﹣2≤a≤2，即a的取值范围是[π﹣2，2]．20．（14分）已知椭圆C：的长轴长为4，离心率为，过右焦点的直线l与椭圆相交于M，N两点，点P的坐标为（4，3），记直线PM，PN的斜率分别为k1，k2．（Ⅰ）求椭圆C的方程；（Ⅱ）当时，求直线l的斜率；（Ⅲ）求证：k1+k2为定值．【解答】解：（Ⅰ）依题意2a＝4，所以a＝2．因为，所以c＝1．所以b2＝3，所以椭圆C的方程为．（Ⅱ）椭圆得右焦点F（1，0）．当直线l的斜率不存在时，不妨取，，|MN|＝3，不合题意．当直线l的斜率存在时，设直线l：y＝k（x﹣1），M（x1，y1），N（x2，y2）．联立方程组，消y得（3+4k2）x2﹣8k2x+4（k2﹣3）＝0，△＞0成立．所以，．因为，即，所以，所以k＝±1．（Ⅲ）证明：当直线l的斜率不存在时，不妨取，，此时．当直线l的斜率存在时，设直线l：y＝k（x﹣1），M（x1，y1），N（x2，y2）．此时．分子化为24﹣3（x1+x2）﹣4（y1+y2）+x2y1+x1y2＝2kx1x2﹣（3+5k）（x1+x2）+8k+24．所以＝＝．综上所述，k1+k2为定值2．。

2018丰台初三数学二模试题及答案丰台区2018年初三统一练习（二）数学试卷2018. 05考生须知1. 本试卷共8页，共三道大题，28道小题，满分100分。

考试时间120分钟。

2. 在试卷和答题卡上认真填写学校名称、姓名和考号。

3. 试题答案一律填涂或书写在答题卡上，在试卷上作答无效。

4. 在答题卡上，选择题、作图题用2B铅笔作答，其他试题用黑色字迹签字笔作答。

5. 考试结束，将本试卷、答题卡一并交回。

一、选择题（本题共16分，每小题2分）第1-8题均有四个选项，符合题意的选项只有．．一个．1．南水北调工程在保障城市供水安全、增加首都水资源战略储备、改善居民生活用水条件、促进水资源涵养和恢复等方面，取得了重大的社会、经济、生态等综合效益.自2008年9月至2018年5月，北京已累计收水超过5 000 000 000立方米.将5 000 000 000用科学记数法表示为（A）100.510⨯（B）10510⨯（C）9510⨯（D）85010⨯2．为丰富国民精神文化生活，提升文化素养，全国各地陆续开展全民阅读活动. 现在的图书馆不单是人们学习知识的地方，更是成为人们休闲的好去处. 下列图书馆标志的图形中不．是．轴对称图形的是（A）（B）（C）（D）3．如图是一个小正方体的展开图，把展开图折叠成小正方体后，有“我”字一面的相对面上的字是（A）厉（B）害（C）了（D）国4．实数a，b，c在数轴上的对应点的位置如图所示，如果a + b = 0，那么下列结论正确的是（A）>a c（B）0a c+<我厉害了的国（C ）0abc <（D ）0a b=5．如图是小明利用等腰直角三角板测量旗杆高度的示意图. 等腰直角三角板的斜边BD与地面AF 平行，当小明的视线恰好沿BC 经过旗杆顶部点E 时，测量出此时他所在的位置点A 与旗杆底部点F 的距离为10米. 如果小明的眼睛距离地面1.7米，那么旗杆EF 的高度为 （A ）10米（B ）11.7米（C ）102米 （D ）(52 1.7)+米 6．已知111m n-=，则代数式222m mn n m mn n --+-的值为 （A ）3 （B ）1（C ）-1（D ）-37．为适应新中考英语听说机考，九年级甲、乙两位同学使用某手机软件进行英语听说练习并记录了40次的练习成绩. 甲、乙两位同学的练习成绩统计结果如图所示：甲同学的练习成绩统计图 乙同学的练习成绩统计图下列说法正确的是（A ）甲同学的练习成绩的中位数是38分 （B ）乙同学的练习成绩的众数是15分（C ）甲同学的练习成绩比乙同学的练习成绩更稳定 （D ）甲同学的练习总成绩比乙同学的练习总成绩低8．某移动通讯公司有两种移动电话计费方式，这两种计费方式中月使用费y （元）与主叫时间x （分）的对应关系如图所示：（主叫时间不到1分钟，按1分钟收费）下列三个判断中正确的是 ① 方式一每月主叫时间为300分钟时，月使用费为88元 ② 每月主叫时间为350分钟和600分钟时，两种方式收费相同③ 每月主叫时间超过600分钟，选择方式一更省钱（A ）①② （B ）①③ （C ）②③ （D ）①②③F AB C DEy /元方式二方式一60088O20013840058二、填空题（本题共16分，每小题2分） 9．分解因式：a 3 - ab 2 = ． 10．正六边形每个内角的度数是 ．11．如果关于x 的不等式ax > 2的解集为x <2a，写出一个满足条件的a = ．12．一个盒子里装有除颜色外都相同的10个球，其中有a 个红球，b 个黄球，c 个白球. 从盒子里随意摸出1个球，摸出黄球的概率是12，那么a = ，b = ，c = ．（写出一种情况即可）13．“复兴号”是我国具有完全自主知识产权、达到世界先进水平的动车组列车.“复兴号”的速度比原来列车的速度每小时快50千米，提速后从北京到上海运行时间缩短了30分钟. 已知从北京到上海全程约1320千米，求“复兴号”的速度.设“复兴号”的速度为x 千米/时，依题意，可列方程为__________________．14．如图，在平面直角坐标系xOy 中，正方形OABC 的边长为1，点D ，E 分别在OA ，OC 上，OD = CE ，△OCD 可以看作是△CBE 经过若干次图形的变化（平移、轴对称、旋转）得到的，写出一种由△CBE 得到△OCD 的过程： ．15．如图，是一辆小汽车与墙平行停放的平面示意图，汽车靠墙一侧OB 与墙MN 平行且距离为0.8米，一辆小汽车车门宽AO 为1.2米，当车门打开角度∠AOB 为40°时，车门是否会碰到墙？ ；（填“是”或“否”）请简述你的理由 ．（参考数据：sin40°≈ 0.64，cos40°≈ 0.77，tan40°≈ 0.84）16．数学课上，老师提出如下问题：△ABC 是⊙O 的内接三角形，OD ⊥BC 于点D .请借助直尺，画出△ABC 中∠BAC 的平分线. 晓龙同学的画图步骤如下： （1）延长OD 交BC 于点M ； （2）连接AM 交BC 于点N.所以线段AN 为所求△ABC 中∠BAC 的平分线. 请回答：晓龙同学画图的依据是 .三、解答题（本题共68分，第17-22，24题每小题5分，第23，25题每小题6分，第26-28题每小题7分）A O BMN17212sin 60(1)2-⎛⎫-︒+-+ ⎪⎝⎭．18．解分式方程：112x x x-=-.19．如图，E ，C 是线段BF 上的两点，BE = FC ，AB ∥DE ，∠A=∠D ，AC=6，求DF 的长.20．在平面直角坐标系xOy 中，已知抛物线y = x 2 - 4x + 2m - 1与x 轴交于点A ，B .（点A 在点B 的左侧） （1）求m 的取值范围；（2）当m 取最大整数时，求点A 、点B 的坐标．21．如图，BD 是△ABC 的角平分线，过点D 作DE ∥BC 交AB 于点E ，DF ∥AB 交BC于点F ．（1）求证：四边形BEDF 为菱形； （2）如果∠A = 90°，∠C = 30°，BD = 12，求菱形BEDF 的面积．22．在平面直角坐标系xOy 中，直线l ：21(0)y mx m m =-+≠. （1）判断直线l 是否经过点M （2，1），并说明理由； （2）直线l 与反比例函数ky x=的图象的交点分别为点M ，N ，当OM =ON 时，直接写出点N 的坐标.DB ADEA23．某校七年级6个班的180名学生即将参加北京市中学生开放性科学实践活动送课到校课程的学习. 学习内容包括以下7个领域：A.自然与环境，B.健康与安全，C.结构与机械，D.电子与控制，E.数据与信息，F.能源与材料，G.人文与历史. 为了解学生喜欢的课程领域，学生会开展了一次调查研究，请将下面的过程补全.收集数据学生会计划调查30名学生喜欢的课程领域作为样本，下面抽样调查的对象选择合理的是___________；（填序号）①选择七年级1班、2班各15名学生作为调查对象②选择机器人社团的30名学生作为调查对象③选择各班学号为6的倍数的30名学生作为调查对象调查对象确定后，调查小组获得了30名学生喜欢的课程领域如下：A，C，D，D，G，G，F，E，B，G，C，C，G，D，B，A，G，F，F，A，G，B，F，G，E，G，A，B，G，G整理、描述数据整理、描述样本数据，绘制统计图表如下，请补全统计表和统计图．某校七年级学生喜欢的课程领域统计表某校七年级学生喜欢的课程领域统计图分析数据、推断结论 请你根据上述调查结果向学校推荐本次送课到校的课程领域，你的推荐是__________（填A-G 的字母代号），估计全年级大约有_________名学生喜欢这个课程领域．24．如图，⊙O 中，AB 是⊙O 的直径，G 为弦AE 的中点，连接OG 并延长交⊙O 于点D ，连接BD 交AE 于点F ，延长AE 至点C ，使得FC = BC ，连接BC . （1）求证：BC 是⊙O 的切线；（2）⊙O 的半径为5，3tan 4A，求FD 的长．25．数学活动课上，老师提出问题：如图，有一张长4dm ，宽3dm 的长方形纸板，在纸板的四个角裁去四个相同的小正方形，然后把四边折起来，做成一个无盖的盒子，问小正方形的边长为多少时，盒子的体积最大. 下面是探究过程，请补充完整：（1）设小正方形的边长为x dm ，体积为y dm 3，根据长方体的体积公式得到y 和x 的关系式： ；（2）确定自变量x 的取值范围是 ； （3）列出y 与x 的几组对应值.（说明：表格中相关数值保留一位小数）（4）在下面的平面直角坐标系xOy 中，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；DEG O F ACB（5）结合画出的函数图象，解决问题：当小正方形的边长约为 dm 时，盒子的体积最大，最大值约为 dm 3.26．在平面直角坐标系xOy 中，二次函数22y x hx h =-+的图象的顶点为点D ．（1）当1h =-时，求点D 的坐标； （2）当1x -≤≤≤1x ≤≤1时，求函数的最小值m ．（用含h 的代数式表示m ）27．如图，正方形ABCD 中，点E 是BC 边上的一个动点，连接AE ，将线段AE 绕点A 逆时针旋转90°，得到AF ，连接EF ，交对角线BD 于点G ，连接AG ． （1）根据题意补全图形；（2）判定AG 与EF 的位置关系并证明；（3）当AB = 3，BE = 2时，求线段BG 的长．AB CE D28．在平面直角坐标系xOy 中，将任意两点()11,y x P 与()22y x Q ，之间的“直距”定义为：2121y y x x D PQ -+-=.例如：点M （1，2-），点N （3，5-），则132(5)5MN D =-+---=.已知点A (1，0)、点B (-1，4).（1）则_______=AO D ，_______=BO D ； （2）如果直线AB 上存在点C ，使得COD 为2，请你求出点C 的坐标；（3）如果⊙B 的半径为3，点E 为⊙B 上一点，请你直接写出EOD 的取值范围.丰台区初三数学参考答案一、选择题（本题共16分，每小题2分） 题号 1 2 3 4 5 6 7 8 答案CBDCBDAA二、填空题（本题共16分，每小题2分）9．()()a a b a b +-； 10．120°； 11．-1（答案不唯一）； 12．2，5，3（答案不唯一）； 13．13201320305060xx =--；14．将△CBE 绕点C 逆时针旋转90°，再向下平移1个单位得到△OCD （答案不唯一）；54411231213xO y6654327654326515．否，求出点A与直线OB的距离d1，通过计算可得d1 <0.8，所以车门不会碰到墙；16．垂径定理，等弧所对的圆周角相等．三、解答题（本题共68分，第17—22、24题，每小题5分；第23，25题6分；第26，27，28题，每小题7分）17．解：23182sin60(1)2-⎛⎫-︒+-+ ⎪⎝⎭．=32214-⨯++……………………4分=73-. ……………………5分18．解：去分母，得x2-x（x-2）=x-2……………………2分解这个方程，得x=-2 ……………………4分经检验x=-2是原方程的解．∴原方程的解是x=-2．………5分19．证明：∵AB∥DE，∴∠ABC=∠DEF. ………………………1分∵BE = FC，∴BE +EC=FC+EC，∴BC=EF．………………………2分又∵∠A=∠D，∴△ABC≌△DEF，………………………3分∴AC=DF．………………………4分又∵AC=6，∴DF=6．………………………5分FDE CBA20．解：（1）∵抛物线y =x 2-4x +2m -1与x 轴有两个交点，令y =0.∴x 2-4x +2m -1=0. ∵ 与x 轴有两个交点， ∴方程有两个不等的实数根.∴Δ>0.即Δ=(-4)2-4•(2m -1)>0∴m <2.5. ………………………2分（2） ∵m <2.5，且m 取最大整数，∴m =2. ………………………3分 当m =2时，抛物线y =x 2-4x +2m -1= x 2-4x +3. 令y =0，得x 2-4x +3=0，解得x 1 = 1，x 2=3.∴抛物线与x 轴两个交点的坐标为A （1，0），B （3，0）. ……………5分21．（1）证明：∵DE ∥BC ，DF ∥AB ，∴四边形BEDF 为平行四边形………………1分∴∠1=∠3.∵BD 是△ABC 的角平分线，∴∠1=∠2. ∴∠2=∠3. ∴BF =DF .∴四边形BEDF 为菱形.………………………2分（2）解：过点D 作DG ⊥BC 于点G ，则∠BGD =90°.∵∠A =90°，∠C =30°，∴∠ABC =60°. 由（1）知，BF =DF ，∠2=30°，DF ∥AB ，∴∠DFG =∠ABC =60°. ∵BD =12，∴在Rt △BDG 中，DG=6.∴在Rt △FDG 中，DF=分 ∴BF =DF=∴S 菱形BEDFBF DG =⋅=. ………………………5分（其他证法相应给分）22．（1）解：直线l 经过点M （2，1）. …….…….…….……1分理由如下：对于21y mx m =-+，令x =2，则2211y m m =-+=∴直线l 经过点M （2，1）. .…….…….……2分（2）点N 的坐标为（1，2），（-2，-1），（-1，-2）. .…….…….……5分23．收集数据 抽样调查对象选择合理的是③. ………………………1分整理、描述数据 如下： ………………………4分G 321ACEDF某校七年级学生喜欢的课程领域统计表 某校七年级学生喜欢的课程领域统计图 E F CDGAB分析数据、推断结论 G ，60. ………………………6分24．（1）证明：∵G 为弦AE 的中点，∴OD ⊥AE .…….…….……………1分∴∠DGC =90°.∴∠D +∠DFG =90°.∵FC =BC ，∴∠1＝∠2. ∵∠DFG =∠1，∴∠DFG ＝∠2. ∵OD =OB ，∴∠D ＝∠3.∴∠3 +∠2=90°. ∴∠ABC ＝90°.即CB ⊥AB.∴BC 是⊙O 的切线. …….…….……………2分（2）解：∵OA =5，tan A =34，∴在Rt △AGO 中，∠AGO ＝90°，OG =3，AG =4. ∵OD =5，∴DG =2. ∵AB =2OA =10，∴在Rt △ABC 中，∠ABC ＝90°，BC =152 ，AC =252.∴FC =BC =152. ∴ 1GF AC AG FC =--=.∴在Rt △DGF 中，FD 分（其他证法或解法相应给分.）25．解：（1）()()4232y x x x =-- .……1分 （2）0<x <1.5. ………………………2分321D E GOF ACB（3）如下表， ………………………4分（4）如右图； ………………………5分 （5）21至85均可，3.0至3.1均可 ………………………6分26．解：（1）∵抛物线22y x hx h =-+=（x -h ）2+h -h 2，∴顶点D 的坐标为（h ，h -h 2），∴当h =-1时，点D 的坐标是（-1，-2）． …………3分（2）当x =-1时，y = 3h+1，当x =1时，y =-h+1． …………4分① 当h <-1时，函数的最小值m = 3h+1 …………5分 ② 当-1≤h ≤1时，，函数的最小值m = h -h 2 …………6分③ 当h >1时，，函数的最小值m =-h+1 …………7分27．解：（1）图形补全后如图…………………1分（2）结论：AG ⊥EF ． …………………2分 证明：连接FD ，过F 点FM ∥BC ，交BD ∵四边形ABCD 是正方形，∴AB=DA=DC=BC ，∠DAB =∠ABE =∠ADC ∠ADB =∠5=45°．∵线段AE 绕点A 逆时针旋转90°，得到AF ， ∴AE=AF ，∠FAE =90°．∴∠1=∠2．∴△FDA ≌△EBA ． …………………3分 ∴∠FDA =∠EBA =90°，FD=BE ． ∵∠ADC =90°，∴∠FDA +∠ADC =180°。

丰台区2018年初三统一练习（二）数 学 试 卷2018. 05考生须知 1. 本试卷共8页，共三道大题，28道小题，满分100分。

考试时间120分钟。

2. 在试卷和答题卡上认真填写学校名称、姓名和考号。

3. 试题答案一律填涂或书写在答题卡上，在试卷上作答无效。

4. 在答题卡上，选择题、作图题用2B 铅笔作答，其他试题用黑色字迹签字笔作答。

5. 考试结束，将本试卷、答题卡一并交回。

一、选择题（本题共16分，每小题2分）第1-8题均有四个选项，符合题意的选项只有．．一个． 1．南水北调工程在保障城市供水安全、增加首都水资源战略储备、改善居民生活用水条件、促进水资源涵养和恢复等方面，取得了重大的社会、经济、生态等综合效益. 自2008年9月至2018年5月，北京已累计收水超过5 000 000 000立方米.将5 000 000 000用科学记数法表示为 （A ）（B ）（C ）（D ）2．为丰富国民精神文化生活，提升文化素养，全国各地陆续开展全民阅读活动. 现在的图书馆不单是人们学习知识的地方，更是成为人们休闲的好去处. 下列图书馆标志的图形中不．是．轴对称图形的是（A ） （B ） （C ） （D ）3．如图是一个小正方体的展开图，把展开图折叠成小正方体后，有“我”字一面的相对面上的字是 （A ）厉 （B ）害 （C ）了（D ）国4．实数a ，b ，c 在数轴上的对应点的位置如图所示，如果a+b=0，那么下列结论正确的是 （A ）（B ）（C ）（D ）5．如图是小明利用等腰直角三角板测量旗杆高度的示意图. 等腰直角三角板的斜边BD 与地面AF 平行，当小明的视线恰好沿BC 经过旗杆顶部点E 时，测量出此时他所在的位置点A 与旗杆底部点F 的距离为米. 如果小明的眼睛距离地面1.7米，那么旗杆EF 的高度为 （A ）米 （B ）米 （C ）米 （D ）米 6．已知，则代数式的值为（A ）3（B ）1 （C ）-1（D ）-37．为适应新中考英语听说机考，九年级甲、乙两位同学使用某手机软件进行英语听说练习并记录了40次的练习成绩. 甲、乙两位同学的练习成绩统计结果如图所示：甲同学的练习成绩统计图 乙同学的练习成绩统计图下列说法正确的是（A ）甲同学的练习成绩的中位数是38分 （B ）乙同学的练习成绩的众数是15分（C ）甲同学的练习成绩比乙同学的练习成绩更稳定（D ）甲同学的练习总成绩比乙同学的练习总成绩低8．某移动通讯公司有两种移动电话计费方式，这两种计费方式中月使用费y （元）与主叫时间x （分）的对应关系如图所示：（主叫时间不到1分钟，按1分钟收费）下列三个判断中正确的是①方式一每月主叫时间为300分钟时，月使用费为88元②每月主叫时间为350分钟和600分钟时，两种方式收费相同③每月主叫时间超过600分钟，选择方式一更省钱我厉 害 了 的国 y /元方式二方式一60088O 20013840058（A ）①② （B ）①③ （C ）②③ （D ）①②③ 二、填空题（本题共16分，每小题2分） 9．分解因式：a 3 - ab 2 = ． 10．正六边形每个内角的度数是 ．11．如果关于x 的不等式ax > 2的解集为x <，写出一个满足条件的a = ． 12．一个盒子里装有除颜色外都相同的10个球，其中有a 个红球，b 个黄球，c 个白球.从盒子里随意摸出1个球，摸出黄球的概率是，那么a = ，b = ，c= ．（写出一种情况即可）13．“复兴号”是我国具有完全自主知识产权、达到世界先进水平的动车组列车.“复兴号”的速度比原来列车的速度每小时快50千米，提速后从北京到上海运行时间缩短了30分钟.已知从北京到上海全程约1320千米，求“复兴号”的速度.设“复兴号”的速度为千米/时，依题意，可列方程为__________________．14．如图，在平面直角坐标系xOy 中，正方形OABC 的边长为1，点D ，E 分别在OA ，OC 上，OD = CE ，△OCD 可以看作是△CBE 经过若干次图形的变化（平移、轴对称、旋转）得到的，写出一种由△CBE 得到△OCD 的过程： ．15．如图，是一辆小汽车与墙平行停放的平面示意图，汽车靠墙一侧OB 与墙MN 平行且距离为0.8米，一辆小汽车车门宽AO 为1.2米，当车门打开角度∠AOB 为40°时，车门是否会碰到墙？ ；（填“是”或“否”）请简述你的理由 ． （参考数据：sin40°≈ 0.64，cos40°≈ 0.77，tan40°≈ 0.84）16．数学课上，老师提出如下问题：△ABC 是⊙O 的内接三角形，OD ⊥BC 于点D .请借助直尺，画出△ABC 中∠BAC 的平分线.晓龙同学的画图步骤如下： （1）延长OD 交于点M ；（2）连接AM 交BC 于点N.所以线段AN 为所求△ABC 中∠BAC 的平分线. 请回答：晓龙同学画图的依据是 .三、解答题（本题共68分，第17-22，24题每小题5分，第23，25题每小题6分，第26-28题每小题7分） 17．计算：．18．解分式方程：.19．如图，E ，C 是线段BF 上的两点，BE = FC ，AB ∥DE ，∠A=∠D ，AC=6，求DF 的长.20．在平面直角坐标系xOy 中，已知抛物线y = x 2 - 4x + 2m -1与x 轴交于点A ，B .（点A 在点B 的左侧） （1）求m 的取值范围；（2）当m 取最大整数时，求点A 、点B 的坐标．21．如图，BD 是△ABC 的角平分线，过点D 作DE ∥BC 交AB 于点E ，DF ∥AB 交BC 于点F ．（1）求证：四边形BEDF 为菱形； （2）如果∠A = 90°，∠C = 30°，BD = 12，求菱形BEDF 的面积．E DCBA y Ox11A O B MND EA22．在平面直角坐标系xOy 中，直线l ：.（1）判断直线l 是否经过点M （2，1），并说明理由； （2）直线l 与反比例函数的图象的交点分别为点M ，N ，当OM =ON 时，直接写出点N 的坐标.23．某校七年级6个班的180名学生即将参加北京市中学生开放性科学实践活动送课到校课程的学习.学习内容包括以下7个领域：A.自然与环境，B.健康与安全，C.结构与机械，D.电子与控制，E.数据与信息，F.能源与材料，G .人文与历史.为了解学生喜欢的课程领域，学生会开展了一次调查研究，请将下面的过程补全. 收集数据学生会计划调查30名学生喜欢的课程领域作为样本，下面抽样调查的对象选择合理的是___________；（填序号）① 选择七年级1班、2班各15名学生作为调查对象 ② 选择机器人社团的30名学生作为调查对象 ③ 选择各班学号为6的倍数的30名学生作为调查对象调查对象确定后，调查小组获得了30名学生喜欢的课程领域如下：A ，C ，D ，D ，G ，G ，F ，E ，B ，G ，C ，C ，G ，D ，B ，A ，G ，F ，F ，A ， G ，B ，F ，G ，E ，G ，A ，B ，G ，G整理、描述数据整理、描述样本数据，绘制统计图表如下，请补全统计表和统计图．某校七年级学生喜欢的课程领域统计表 某校七年级学生喜欢的课程领域统计图分析数据、推断结论 请你根据上述调查结果向学校推荐本次送课到校的课程领域，你的推荐是__________（填A-G 的字母代号），估计全年级大约有_________名学生喜欢这个课程领域．24．如图，⊙O 中，AB 是⊙O 的直径，G 为弦AE 的中点，连接OG 并延长交⊙O 于点D ，连接BD 交AE 于点F ，延长AE 至点C ，使得FC = BC ，连接BC . （1）求证：BC 是⊙O 的切线； （2）⊙O 的半径为5，，求FD 的长．4411231213x O y 43243225．数学活动课上，老师提出问题：如图，有一张长4dm ，宽3dm 的长方形纸板，在纸板的四个角裁去四个相同的小正方形，然后把四边折起来，做成一个无盖的盒子，问小正方形的边长为多少时，盒子的体积最大. 下面是探究过程，请补充完整： （1）设小正方形的边长为x dm ，体积为ydm 3，根据长方体的体积公式得到y 和x 的关系式： ；（2）确定自变量x 的取值范围是 ； （3）列出y 与x 的几组对应值.x /dm …1… y /dm 3 … 1.3 2.2 2.73.0 2.8 2.51.5 0.9 …（说明：表格中相关数值保留一位小数） （4）在下面的平面直角坐标系中，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；3Oyx421123（5）结合画出的函数图象，解决问题：当小正方形的边长约为 dm 时，盒子的体积最大，最大值约为 dm 3.26．在平面直角坐标系xOy 中，二次函数的图象的顶点为点D ．（1）当时，求点D 的坐标；（2）当≤≤时，求函数的最小值m ．（用含h 的代数式表示m ）27．如图，正方形ABCD 中，点E 是BC 时针旋转90°，得到AF ，连接EF ，交对角线BD 于点G ，连接AG ． （1）根据题意补全图形；（2）判定AG 与EF 的位置关系并证明；（3）当AB = 3，BE = 2时，求线段BG 的长．28．在平面直角坐标系xOy 中，将任意两点与之间的“直距”定义为：.例如：点M （1，），点N （3，），则.已知点A (1，0)、点B (-1，4). （1）则，；（2）如果直线AB 上存在点C ，使得为2，请你求出点C 的坐标；（3）如果⊙B 的半径为3，点E 为⊙B 上一点，请你直接写出的取值范围.丰台区2018年初三第二次统一练习 54411231213xOy68765432765432654411231213xO y432432初三数学参考答案一、选择题（本题共16分，每小题2分）题号 1 2 3 4 5 6 7 8答案 C B D C B D A A二、填空题（本题共16分，每小题2分）；答案不唯一）（1-．11；120°．10；．912．2，5，3（答案不唯一）；13．；14．将△CBE绕点C逆时针旋转90°，再向下平移1个单位得到△OCD（答案不唯一）；15．否，求出点A与直线OB的距离d1，通过计算可得d1 <0.8，所以车门不会碰到墙；16．垂径定理，等弧所对的圆周角相等．三、解答题（本题共68分，第17—22、24题，每小题5分；第23，25题6分；第26，27，28题，每小题7分）17．解：．=……………………4分=. ……………………5分18．解：去分母，得x2-x（x-2）=x-2……………………2分解这个方程，得x=-2 ……………………4分经检验x=-2是原方程的解．∴原方程的解是x=-2．………5分19．证明：∵AB∥DE，∴∠ABC=∠DEF. ………………………1分∵BE = FC，∴BE +EC=FC+EC，∴BC=EF．………………………2分又∵∠A=∠D，∴△ABC≌△DEF，………………………3分∴AC=DF．………………………4分又∵AC=6，∴DF=6．………………………5分20．解：（1）∵抛物线y=x2-4x+2m-1与x轴有两个交点，令y=0.∴x2-4x+2m-1=0. ∵与x轴有两个交点，∴方程有两个不等的实数根.∴Δ>0.即Δ=(-4)2-4•(2m-1)>0∴m<2.5. ………………………2分（2）∵m<2.5，且m取最大整数，∴m=2. ………………………3分当m=2时，抛物线y=x2-4x+2m-1= x2-4x+3.令y=0，得x2-4x+3=0，解得x1=1，x2=3.∴抛物线与x轴两个交点的坐标为A（1，0），B（3，0）. ……………5分21．（1）证明：∵DE∥BC，DF∥AB，∴四边形BEDF为平行四边形………………1分∴∠1=∠3.∵BD是△ABC的角平分线，∴∠1=∠2.∴∠2=∠3. ∴BF=DF.∴四边形BEDF为菱形.………………………2分（2）解：过点D作DG⊥BC于点G，则∠BGD=90°.∵∠A=90°，∠C=30°，∴∠ABC=60°.由（1）知，BF=DF，∠2=30°，DF∥AB，∴∠DFG=∠ABC=60°.∵BD=12，∴在Rt△BDG中，DG=6.∴在Rt△FDG中，DF=. ………………………4分∴BF= DF=.∴S菱形BEDF. ………………………5分（其他证法相应给分）22．（1）解：直线l经过点M（2，1）. …….…….…….……1分理由如下：对于，令x=2，则∴直线l经过点M（2，1）. .…….…….……2分（2）点N的坐标为（1，2），（-2，-1），（-1，-2）. .…….…….……5分23．收集数据抽样调查对象选择合理的是③. ………………………1分整理、描述数据如下：………………………4分某校七年级学生喜欢的课程领域统计表某校七年级学生喜欢的课程领域统计图课程领域人数F 4G 10G321ABED54321H M GFABD CE 分析数据、推断结论 G ，60. ………………………6分 24．（1）证明：∵G 为弦AE 的中点，∴OD ⊥AE . …….…….……………1分∴∠DGC =90°.∴∠D +∠DFG =90°.∵FC =BC ，∴∠1＝∠2. ∵∠DFG =∠1，∴∠DFG ＝∠2. ∵OD =OB ，∴∠D ＝∠3.∴∠3 +∠2=90°. ∴∠ABC ＝90°.即CB ⊥AB.∴BC 是⊙O 的切线. …….…….……………2分（2）解：∵OA =5，tan A =，∴在Rt △AGO 中，∠AGO ＝90°，OG =3，AG =4. ∵OD =5，∴DG =2. ∵AB =2OA =10，∴在Rt △ABC 中，∠ABC ＝90°，BC = ，AC =.∴FC =BC =. ∴.∴在Rt △DGF 中，FD =. …5分（其他证法或解法相应给分.）25．解： （1）.……1分（2）0<x <1.5. ………………………2分 （3）如下表， ………………………4分x /dm1y /dm 3.0 2.0（4）如右图； ………………………5分 （5）至均可，3.0至3.1均可 ………………………6分26．解：（1）∵抛物线=（x -h ）2+h -h 2，∴顶点D 的坐标为（h ，h -h 2），∴当h =-1时，点D 的坐标是（-1，-2）． …………3分（2）当x =-1时，y = 3h+1，当x =1时，y =-h+1． …………4分 ① 当h <-1时，函数的最小值m = 3h+1 …………5分② 当-1≤h ≤1时，，函数的最小值m = h -h 2 …………6分 ③ 当h >1时，，函数的最小值m =-h+1 …………7分27．解：（1）图形补全后如图…………………1分GFAB DCE（2）结论：AG ⊥EF ． …………………2分证明：连接FD ，过F 点FM ∥BC ，交BD 的延长线于点M ．∵四边形ABCD 是正方形，∴AB=DA=DC=BC ，∠DAB =∠ABE =∠ADC =90°， ∠ADB =∠5=45°．∵线段AE 绕点A 逆时针旋转90°，得到AF ， ∴AE=AF ，∠FAE =90°． ∴∠1=∠2．∴△FDA ≌△EBA ． …………………3分 ∴∠FDA =∠EBA =90°，FD=BE ． ∵∠ADC =90°，∴∠FDA +∠ADC =180°。

丰台2018高三二模 2018.5高三数学（文科）参考答案二、填空题：本大题共6小题，每小题5分，共30分。

（9）25-（10） 5 （11）50x +-=（12）2；π6（13）1-；1,4,2-∞-（）（-1-） （14）①② 注：第12，13题第一个空填对得3分，第二个空填对得2分． 第14题只写对一个得2分，有一个错误不得分．三、解答题：本大题共6小题，共80分。

解答应写出文字说明，演算步骤或证明过程。

（15）（本小题共13分） 解：（Ⅰ）在△ADB 中，由余弦定理得222cos2AD BD AB ADB AD BD +-∠=⋅100361962106+-=⨯⨯12=-． …………………2分 因为 (0,π)ADB ∠∈， …………………3分 所以2π3ADB ∠=． …………………5分 （Ⅱ）由 cos DAC ∠=，可知sin DAC ∠=， …………………6分 所以2πsin sin()3C DAC ∠=-∠ …………………8分 12142147=⨯+⨯=． …………………10分 在△ADC 中，由正弦定理得sin sin AC ADADC C=∠∠， …………………12分 所以=所以 AC = …………………13分（16）（本小题共13分） 解：（Ⅰ）因为 23n S n =，所以 113a S ==． …………………1分 当2n ≥时，1n n n a S S -=-2233(1)n n =--63n =-．…………………3分 因为当 1n =时，16133a ⨯-==， …………………4分 所以数列{}n a 的通项公式是 63n a n =-． …………………5分 （Ⅱ）设数列{}n b 的公比为q ．因为 113a b =，所以 11b =． (6)分因为 242b b a ⋅=， 所以 239b =． …………………8分因为 2310b b q =>，所以 33b =，且23q =． (10)分因为{}n b 是等比数列，所以21{}n b -是首项为11b =，公比为23q =的等比数列． (11)分所以 212(1())131(31)1132n n nn b q T q --===---． 即 1(31)2nn T =-． …………………13分（17）（本小题共14分）证明：（Ⅰ）因为 1A D ⊥平面ABC ，所以 1A D ⊥AC ． …………………1分 因为△ABC 中，=AB BC ，D 是AC 的中点，所以 BD AC ⊥． …………………2分 因为 1A DBD D =， …………………3分所以 AC ⊥平面1A BD ． …………………4分 所以 1AC A B ⊥． …………………5分 （Ⅱ） 因为 1A D ⊥平面ABC ，因为 BD ⊂平面ABC ，所以 1A D BD ⊥． …………………6分 由（Ⅰ）知 BD AC ⊥． 因为 1ACA D D =， …………………7分所以 BD ⊥平面11A ACC ． …………………8分 因为 BD ⊂平面1BB D ，所以 平面1BB D ⊥平面11AAC C ． …………………9分 （Ⅲ）因为在三棱柱111ABC A B C -中，侧面11A ABB 为平行四边形，所以 11B B A A ∥． …………………10分 因为 1B B ⊄平面11A ACC ，1A A ⊂平面11A ACC ， …………………11分 所以 1B B ∥平面11A ACC ． …………………12分 因为 1B B ⊂平面1BB D ，且平面1BB D平面11A ACC DE =， (13)分所以 1B B DE ∥． …………………14分（18）（本小题共13分） 解：（Ⅰ）A 组平均值为：2808340338332330230225225220=+++++++；……………1分B 组平均值为：2002202303323383403603803008+++++++=．……………2分（Ⅰ）将A 组客户中实际平均续航里程数为338, 340的客户分别记为1a ，2a ；将B 组客户中实际平均续航里程数为338, 340, 360, 380的客户分别记为1b ，2b ，3b ，4b ． 从A ，B 两组实际平均续航里程数大于335km 的客户中各随机抽取1位客户的事件包括：11b a ，21b a ，31b a ，41b a ，12b a ，22b a ，32b a ，42b a ，共8种， …………………5分其中A 组客户的实际平均续航里程数不小于B 组客户的实际平均续航里程数的事件包括：11b a ，12b a ，22b a ，共3种． (7)分设“A 组客户的实际平均续航里程数不小于B 组客户的实际平均续航里程数”为事件M ， …………………8分则3()8P M =． …………………10分 所以A 组客户的实际平均续航里程数不小于B 组客户的实际平均续航里程数的概率为38．（III ）A 组数据的方差小于B 组数据的方差． …………………13分（19）（本小题共13分）解：（Ⅰ）()()sin f x x a x '=--． …………………2分因为 (0,π)x ∈，所以 sin 0x >． .....................3分 由 ()0f x '=得 x a =． (4)分当0a ≤时，()0f x '<，()f x 在(0,π)上单调递减； …………………5分 当πa ≥时，()0f x '>，()f x 在(0,π)上单调递增； …………………6分 当0πa <<时，x ，()f x '，()f x 的变化情况如下表：所以()f x 的单调递增区间是(0,)a ，单调递减区间是(,π)a ． 综上所述，当0a ≤时，()f x 在(0,π)上单调递减； 当πa ≥时，()f x 在(0,π)上单调递增；当0πa <<时，以()f x 的单调递增区间是(0,)a ，单调递减区间是(,π)a ．………9分 （Ⅱ）设 2()21g x x x =--．因为 2()(1)2g x x =--，当1x =时，()g x 有最小值为2-． (10)分因为对于任意1(0,π)x ∈，存在2(0,π)x ∈，都有 2122()21f x x x >--，所以 (0)2(π)2f f ≥-⎧⎨≥-⎩， 即2(π)2a a -≥-⎧⎨--≥-⎩． 所以π22a -≤≤，即a 的取值范围是[π2,2]-． …………………13分（20）（本小题共14分）（Ⅰ）解：依题意 24a =，所以 2a =． …………………1分因为 12c e a ==，所以 1c =． …………………2分所以 23b =， …………………3分所以椭圆C 的方程为 22143x y +=．…………………4分 （Ⅱ）解：椭圆得右焦点(1,0)F ．当直线l 的斜率不存在时，不妨取3(1,)2M ，3(1,)2N -，3MN =，不合题意． (5)分当直线l 的斜率存在时，设直线l ：(1)y k x =-，11(,)M x y ，22(,)N x y ． …………………6分联立方程组 ⎪⎩⎪⎨⎧-==+)1(13422x k y y x ， 消y 得 2222(34)84(3)0k x k x k +-+-=，0∆>成立． (7)分所以 2122834k x x k +=+，21224(3)34k x x k-=+． …………………8分因为247MN ==， …………………9分247=，所以2212347k k +=+，所以1k =±． …………………10分 （Ⅲ）证明：当直线l 的斜率不存在时，不妨取3(1,)2M ，3(1,)2N -，此时123922233k k +=+=． …………………11分当直线l 的斜率存在时，设直线l ：(1)y k x =-，11(,)M x y ，22(,)N x y ． 此时21211221221121)(416)4)(3()4)(3(4343x x x x x y x y x y x y k k ++---+--=--+--=+． 分子化为21122121)(4)(324y x y x y y x x +++-+-248))(53(22121++++-=k x x k x kx ．所以222222222143)3(4438416248438)53(43)3(42k k k k k k k k k k k k k +-++⨯-+++⨯+-+-⨯=+ )3(8)43(4)43)(3(2)53(2)3(2222222-+-+++++--⨯=k k k k k k k k k 299181822=++=k k ．综上所述，12k k +为定值2． …………………14分。