当前位置：文档之家 › 4、高级实验设计—回归的旋转设计(Regressional Rotary Design)

4、高级实验设计—回归的旋转设计(Regressional Rotary Design)

  • 格式：ppt
  • 大小：3.34 MB
  • 文档页数：91

下载文档原格式

  / 91

合集下载

旋转课程设计

旋转课程设计

旋转课程设计一、教学目标本节课的学习目标包括知识目标、技能目标和情感态度价值观目标。

知识目标要求学生掌握旋转的定义、性质和计算方法；技能目标要求学生能够运用旋转的知识解决实际问题；情感态度价值观目标要求学生培养对数学的兴趣和自信心，培养合作意识和探究精神。

二、教学内容本节课的教学内容主要包括旋转的定义、性质和计算方法。

首先，通过实例引入旋转的概念，让学生感知旋转的现象；然后，引导学生探究旋转的性质，如旋转前后的图形形状和大小不变，对应点、对应线段和对应角的关系等；最后，教授旋转的计算方法，如旋转变换的矩阵表示和旋转变换的性质。

三、教学方法为了激发学生的学习兴趣和主动性，本节课采用多种教学方法。

首先，采用讲授法，系统地讲解旋转的定义、性质和计算方法；其次，运用讨论法，让学生在小组内交流探究旋转的性质，培养学生的合作意识和探究精神；最后，运用案例分析法，让学生举例说明旋转在实际问题中的应用，提高学生运用知识解决实际问题的能力。

四、教学资源为了支持教学内容和教学方法的实施，丰富学生的学习体验，本节课准备了一定的教学资源。

教材《数学》提供了本节课的主要学习内容；参考书《数学教程》为学生提供了额外的学习材料；多媒体资料包括旋转的动画和实例视频，帮助学生形象地理解旋转的概念；实验设备如几何画板和折纸，让学生亲自动手操作，感受旋转的现象。

五、教学评估本节课的评估方式包括平时表现、作业和考试。

平时表现主要评估学生的课堂参与度和合作意识，通过观察和记录学生在课堂上的表现来进行评估。

作业评估学生的理解和运用知识的能力，通过作业的完成质量来评估学生的学习效果。

考试则评估学生对旋转知识的掌握程度，包括选择题、填空题和解答题等形式。

六、教学安排本节课的教学安排如下：共安排4个课时，每个课时45分钟。

第一课时介绍旋转的定义和性质，第二课时讲解旋转的计算方法，第三课时进行实例分析和练习，第四课时进行总结和复习。

教学地点安排在教室，利用多媒体设备和实验设备进行教学。

回归旋转试验设计dolly

回归旋转试验设计dolly


• 结果显示，x2最不显著，所以考虑剔除此 变量，且x3比较好，变量变为x3，x1*x3， x3*x3。
• • • • • • • • • • • • • • •
data ex; input x1 x2 x3 y; X4=x3*x3;x5=x1*x3; cards; 1.0 13 1.5 0.330 1.4 19 3.0 0.366 1.8 25 1.0 0.294 2.2 10 2.5 0.476 2.6 16 0.5 0.209 3.0 22 2.0 0.451 3.4 28 3.5 0.482 ; proc glm ; model y=x3 x4 x5; run;
• Y=0.315x3-0.759x3*x3+0.026x1*x3
• • • • • • • • • • • • • • •
data ex; input x1 x2 x3 y; X4=x3*x3;x5=x1*x3; cards; 1.0 13 1.5 0.330 1.4 19 3.0 0.366 1.8 25 1.0 0.294 2.2 10 2.5 0.476 2.6 16 0.5 0.209 3.0 22 2.0 0.451 3.4 28 3.5 0.482 ; proc glm ; model y=x3 x4 x5/noint; run;
一．回归旋转设计的步骤
1. 确定参与试验的因素，选定处理水平。 设某试验p个因素，以z1、z2、zp表 示，每个处理因素设上下两个水平， 第j个因素的上水平为z2j，下水平为 z1j，则各处里的零水平为 z0j＝（ z1j + z2j ）/2
2. 计算各因素的变化区间，并对处理水平 编码。 将第j因素的变化区间以Δ j表示， Δ j＝ （ z2j – z1j ）/2，然后对每个因素zj的 处理水平进行编码，即对每个因素的取 值进行线性变换，因素zj与规范变量xj 变换的对应关系是xj＝（zj-z0j）/ Δ j， 上、下、零水平的编码值分别为+1、-1、 0。
回归设计

回归设计


谢谢观看
自然因素：是未经编码的因素，通常记为z1, z2, ….. zp。自然因素有些有量纲，有些无量纲，但都有具 体的物理意义，由自然因素构成的空间称为自然空间，是实际试验方案存在的空间。
编码因素：是经过编码的因素，通常记为x1, x2, ….. xp。任何编码因素都是无量纲的。由编码因素构成 的空间称为编码空间。回归设计时，方案的编制、回归系数的计算及回归方程的统计检验，即整个优化过程都是 在编码空间进行的。不同的回归设计，有不同的编码公式。
回归设计
应用回归分析时通过试验点的选择、使设计矩阵具有某种优良性的 方法
01 发展历史
03 特点 05 关键
目录
02 相关信息 04 优势 06 应用
基本信息
回归设计是应用回归分析时，通过试验点的选择，使设计矩阵具有某种优良性的一类方法。根据实际问题的 分析要求，恰当选取回归变量值，以尽可能少的观测次数，获得响应变量的最大信息的观测结果，以提高经验回 归方程的精度。常用的有回归正交设计、回归旋转设计、D最优设计、G最优设计等。
为了适应寻求最佳工艺、最佳配方、建立生产过程的数学模型等的需要，人们就要求以较少的试验次数建立 精度较高的回归方程。
为此，要求摆脱古典回归分析的被动局面，主动把试验的安排、数据的处理和回归方程的精度统一起来考虑， 即根据试验目的和数据分析的要求来选择试验点，不仅使得在每一个试验点上获得的数据含有最大的信息，从而 减少试验次数，而且使数据的统计分析具有一些较好的性质。
发展历史
发展历史
回归设计实际上产生于上世纪五十年代，它是综合回归分析与试验设计的现代发展而建立起来的试验优化领 域的一个新分支，也是数理统计学科的一个新发展。它将方案设计、数据处理与回归方程的精度统一起来进行优 化，已成为现代通用的一种试验优化技术。我们知备试验设计很难用于系统连续优化，因为它不能给出连续模型。 由于某些因素水平变化的非定量性和非连续性，即使利用试验数据线性结构模型或伪变量回归分析建立起预测方 程，也只能近似选优。相反，回归设计则提供了便于系统连续优化和进一步精确选优的条件。由此，回归设计不 但使工程技术、自然科学和社会科学乃至思维科学中具有相关关系的多因素问题，都有可能实现定量分析，而且 有可能用最小的代价达到寻优的目的，不论那些问题是白色系统、灰色系统还是黑色系统。可以预料过去那些只 能进行定性研究和处理的科研和生产问题，可以期望用回归设计技术构造需要的数学模型，将其提高到定量分析 的水平上来，加以更好地研究。
第六章 §6 二次回归的旋转设计

第六章 §6 二次回归的旋转设计


五,k>2 实现旋转设计借助于组合设计思想
1.中心组合思想
(1)m c 个点布置在半径 R c = k的球面上 (2 )2k个点布置在半径 R = r的球面上,通常位于 (3)m 0 个点布置在因子区域的 中心
n = m c + 2k + m 0 坐标轴上,称 r为星号臂
2. k = 2 D = 1 1 1 1 r r 0 0 0 0 1 1 1 1 0 0 r r 0 0
§6 二次回归的旋转设计
一,问题
y = β 0 + ∑ βi x i + ∑ βij x i x j + ∑ β ii x i2 + ε
i i< j i
要寻找旋转设计 D, X′X满足旋转性条件 0 第 (0,)元素为 n x 2 = λ 2 n i = 1, , k ∑ ji j ∑ x 4 = 3∑ x 2 1 x 2 2 = 3λ 4 n i1 ≠ i 2 ji ji ji j j k λ4 ≠ 2 λ2 k + 2
∑x
j j
ji
= ∑ x ji1 x ji 2 = ∑ x x ji 2 = 0
2 ji1 j j
x 2 = 4 + 2r 2 ∑ ji x21x2 2 = 4 ∑ ji ji
j
x 4 = 4 + 2r 4 ∑ ji
j
为满足旋转性条件
∑x
j
4 ji
= 3∑ x x
2 ji1 j
2 ji 2
∴ 4 + 2 r 4 = 12 r =
2
3.k ≥ 3
∑x
j j
ji
= ∑ x ji1 x ji 2 = ∑ x 2 1 x ji 2 = 0 ji
二次回归正交旋转组合设计在紫芝液体发酵培养条件优化中的应用

二次回归正交旋转组合设计在紫芝液体发酵培养条件优化中的应用


成分 ， 势必成 本过 高 ， 得对 紫芝深 层次 开发 受到 限 使 制 。利 用液 体深层发 酵技 术可 以在 较短 时 间内获 得
大量菌 丝体及 其发 酵 产 物 ， 以为 大 通 量 开 发 紫芝 可 相 关产 品提供 可 能 。 目前 ， 于 紫 芝 栽 培 和液 体 关 发 酵条件 的研 究 报 道 较 少 ， 无 利 用 五 因素 “ 次 更 二
得其 子实体 ， 但人 工栽 培紫芝 具有 周期 长 ， 成本高 的
缺点 。如果 从子 实体 中提取具 有疗 效 和保健 功能 的
芝科 （ ａ ｏｅｍａ ｃａ ） 灵 芝属 （ ａ ｏ ｅｎ ） 的 Ｇ ｎ ｄ ｒ ｔ ｅｅ ， ａ Ｏ ｎ ｄｒ ａ 中 ｌ 真菌 … 。 自古 以来 被视 为 滋 补 强壮 、 固本 扶正 的珍
西
南
农
业
学
报
２ ３卷
回归 系数之 间相关 性等特 点 ； 二 ， 第 有助 于克服 回归 正 交 设 计 中二 次 回归 预 测 值 ｌ的方 差依 赖 于试 验 ， 点 在 因子空 间 中的位 置 缺点 ， 能有效 地 克Ｊ － 次 即 Ｊ ￣
后 分别在 ２ 、５ ２ 、９ ３ ３ ２ 、７ ２ 、 ｌ℃ 下 ， 每组 ３个 重 复 ， 摇 床培养 。 １３ ５ 依据 单 因素试 验 的结果 确 定 因素 水 平 范 围 ．． 选 取 装 液 量 （ ５ Ｌ 三 角 瓶 ）（ 、 始 ｐ ２０ ｍ Ｘ ）初 Ｈ
１ ３ ６ 不 同接 种 菌龄 对发 酵 的 影 响 分别 向培 养 ．． 液 中接 人菌龄 为 ４ ５ ６ ７ ８ ９ ｄ的种 子 ， 组 ３个 、 、 、 、 、 每
１ 材 料 与 方 法
１ １ 材料 ．
第十讲(2) 旋转D最优设计

第十讲(2) 旋转D最优设计


14
当p=2时的饱和D—最优计划。
试验号 1 2 3 4 5 6 7 8
6点设计
7点设计
8点设计
x1
x2
x1
x2
x1
x2
-1 -1 -1 -1 1 -1 1 -1 -1 1 -1 1 -0.1315 -0.1315 1 1 1 0.3945 -0.092 0.092 0.3945 1 1 -0.067 0.067 -1
-1 -1 1 -1 -1 1 -1 -1 -1 0.1925 0.1925 -1 0.1925 0.1925 -0.2912 1 1 -0.2912 1 1
p=3时的饱和设计称为310设计。
16
关于p4的饱和D—最优计划问题，至今尚未解决。 对于p=4，有人找到了一个较好的15点设计 。见188页 表9-3。 根据p=2,3的二次饱和D—最优计划的谱点结构，得 到一般的二次饱和设计的方案表9-4(188页)。
当p=4时，D—最优计划是：
12
当p=4时，D—最优计划是：
x1 1 1 -1 -1 1 x2 -1 1 -1 -1 1 x3 1 -1 1 -1 1 x4 -1 1 1 -1 -1
一般地，当p+1是2的整数次幂时，p个因子的一 次饱和D—最优计划可用2p型的全因子试验的部分 实施法给出。
13
二、二次饱和Ｄ—最优设计 对二次回归模型
定义在因子空间中若试验计划使a达到最大或使c达到最小即定义在因子空间中若试验计划使a达到最大或使c达到最小即则称为一个d最优计划设计
第八章
回归的旋转设计
回归正交设计的优点：(1)试验次数少；(2)计算简便； (3)消除了回归系数间的相关性。缺点：二次回归的预测 值y的方差依赖于试验点在因子空间的位置，不能根据 预测值直接寻找最优区域。为此提出回归的旋转设计 (旋转性)。它不仅克服了正交设计的缺点，还能基本保 留其优点。
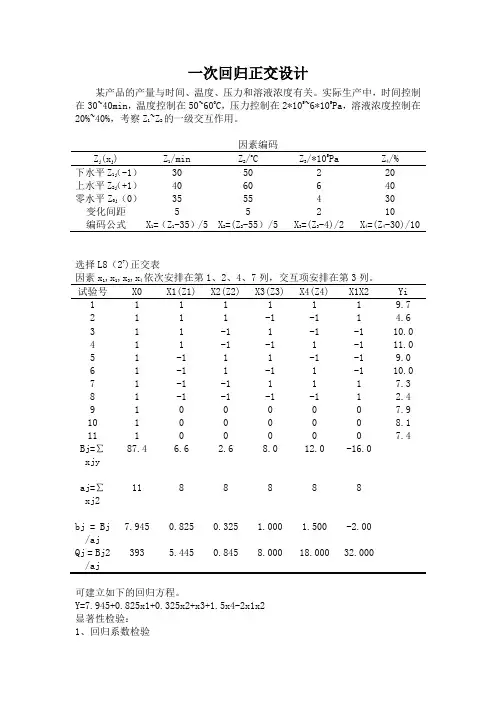
一次回归正交设计、二次回归正交设计、二次回归旋转设计

一次回归正交设计、二次回归正交设计、二次回归旋转设计

一次回归正交设计某产品的产量与时间、温度、压力和溶液浓度有关。

实际生产中，时间控制在30~40min，温度控制在50~600C，压力控制在2*105~6*105Pa，溶液浓度控制在20%~40%，考察Z1~Z2的一级交互作用。

因素编码Z j (xj) Z1/min Z2/o C Z3/*105Pa Z4/%下水平Z1j（-1）30 50 2 20上水平Z2j（+1）40 60 6 40零水平Z0j（0）35 55 4 30 变化间距 5 5 2 10编码公式X1=（Z1-35）/5 X2=(Z2-55）/5 X3=(Z3-4)/2 X4=(Z4-30)/10选择L8（27)正交表因素x1,x1,x3,x4依次安排在第1、2、4、7列，交互项安排在第3列。

试验号X0 X1(Z1) X2(Z2) X3(Z3) X4(Z4) X1X2 Yi1 1 1 1 1 1 1 9.72 1 1 1 -1 -1 1 4.63 1 1 -1 1 -1 -1 10.04 1 1 -1 -1 1 -1 11.05 1 -1 1 1 -1 -1 9.06 1 -1 1 -1 1 -1 10.07 1 -1 -1 1 1 1 7.38 1 -1 -1 -1 -1 1 2.49 1 0 0 0 0 0 7.910 1 0 0 0 0 0 8.111 1 0 0 0 0 0 7.4 Bj=∑xjy87.4 6.6 2.6 8.0 12.0 -16.0aj=∑xj211 8 8 8 8 8bj = Bj/aj7.945 0.825 0.325 1.000 1.500 -2.00Qj = Bj2/aj393 5.445 0.845 8.000 18.000 32.000可建立如下的回归方程。

Y=7.945+0.825x1+0.325x2+x3+1.5x4-2x1x2显著性检验：1、回归系数检验回归关系的方差分析表变异来源SS 平方和 Df 自由度 MS 均方 F 显著水平x 1 5.445 1 5.445 76.25 0.01x 2 0.845 1 0.845 11.83 0.05x 3 8.000 1 8.000 112.04 0.01x4 18.000 1 18.000 252.10 0.01x1x2 32.000 1 32.000 448.18 0.01回归 64.29 5 12.858 180.08 0.01 剩余 0.357 5 0.0714 失拟0.09730.03230.25<1误差e 0.26 2 0.13总和 64.647 10经F 检验不显著的因素或交互作用直接从回归方程中剔掉，不必再重新进行回归分析。

第5讲(2) 正交回归设计

第5讲(2) 正交回归设计


n mc 2 p m0 2 2 2 2 3 11
h mc 2 2 2 1.148 6.636
2 2 2
则
2 2 xj x 2 h / n x 6 . 636 / 11 x j j j 0.603
j 1,2
(5.4.16)
其中指数如上所述，n是试验次数，a a1 a2 a p ， a 是待 定参数，下标a 必为偶数，且 0 1 。
特例：对d=1,2的旋转性条件具体化。 （1） d=1的情况：在一次回归旋转设计，此时A中满足
0 a1 a2 a都是偶数或零这些条件的，应有
5.写出二次回归方程并求最佳条件 我们可以写出在0.10水平上各系数都显著的回归方程为：
35.868x2 ˆ 171.45 14.338x2 21.818x1 y
再将(5.4.16)代入，即可得y关于x1,x2的二次回归方程：
2 ˆ 171.45 14.338 x2 21.818( x12 0.603) 35.868( x2 y 0.603)


2．试验计划与试验结果 本例的试验计划见表5.4.5，在试验随机化后所得试验结果 列在该表的最右边一列。 表5.4.5 试验计划与试验结果
3．参数估计 为求出y关于x1 , x2 的二次回归方程，首先将 x12 与 x22 列中心化， 即令 x x h / n 。在本例中：
j 2 j
§5.5 二次回归旋转设计
5.5.1 旋转性条件与非退化条件
回归正交设计的最大优点是试验次数较少，计算简便， 又消除了回归系数间的相关性。但是其缺点是预测值的方 差依赖于试验点在因子空间中的位置。由于误差的干扰， 试验者不能根据预测值直接寻找最优区域。若能使二次设 计具有旋转性，即能使与试验中心距离相等的点上预测值 的方差相等，那就有助于克服上述缺点。所以试验者常常 希望牺牲部分的正交性而获得旋转性，特别在计算机软件 发展的今天，计算的不便之处可以交由计算机帮助处理。
第六章 §4 旋转回归设计的概念

第六章 §4 旋转回归设计的概念

i
j = 1,2, , n
1 Var β = (X ′X ) σ 2 2 i
1 2 k 1 2 2 = σ + ∑ σ xi n i =1 n 1 2 2 = σ 1+ x n x 就是预测点 x到因子区域中心之间的 距离
(
)
四,使拟合线性回归的单纯形设计具有 旋转性
缺点:一般而言回归预测值y的方差依赖于试验
二,旋转回归设计 旋转设计是使得在离开因子区域的 中心等距离的任意两点处,估计量y 具有相同精度的一种回归设计
三,用正交表对线性回归模型所作的正 交设计是旋转设计
设 y j = β 0 + β1 x 1 + + β k x k + ε j X = (1n , D ) X ′X = nI k +1 ∴ Var (y (x )) = Var β 0
Var(y(x )) = Varβ0 + ∑ Var βi x i2
i =1
k
( )
1 2 k σ2 = σ +∑ 2 x i2 2 k +1 i + i x1i i =1
(
)
取这一点的坐标使 1 1 1 1 = 2 == 2 = 2 2 2x11 6x12 k + k x1k C
(
)
σ2 1 ∴ Var(y(x )) = + x k +1 C
§4 旋转回归设计
一,正交回归设计的优缺点
(1 优点: )计算方便
(2)消除了回归系数间的相关性
点在因子空间中的位置,这就影响了不同 点间预测值的比较,使设计在各个方向上 不能提供等精度的估计,假如能使二次设 计具有旋转性,即能使与试验中心距离相 等的点上,预测值的方差相等,那将有助 于克服上述缺点.
回归的旋转设计教育课件

回归的旋转设计教育课件


在组合设计下，当 mc＝2m （全实施）时，则前式变为
2m2432m
解此方程，即可建立全实施时 γ 值的计算式，即
m
24
(13－31)
同理
m2 2 当
m 1（ 1实 施 ）
c
2
m 1 4
m2 2 当
m 2（ 1实 施 ）
c
4
m 2 4
m2 2 当
m 3（ 1实 施 ）
旋转性对试验设计有什么要求以及获得旋转性必须满足哪
些基本条件。首先必须明确的是：在旋转设计中，试验处
理的预测值ຫໍສະໝຸດ y的方差仅与因素空间中从试验点到试验中心
的距离 ρ 有关而与方向无关，从而克服了通常因为不知道
最优点在什么方向的缺陷。
§1 旋转设计的基本原理
这里应该解决的是二次回归正交的旋转性问题。下面以试验设计中常用的 三元二次回归方程来讨论这个问题。
x2 i
mc2
2

x4 i
mc2
4

均不等于零，完全符合式(13－29)的要求。
x x m 2 2
i j
c

§1 旋转设计的基本原理
为了获得旋转设计方案，还必须根据旋转性条件式(13－29)确定 γ 值，
x xx 事实上只要
4
j
3
2
i
2
j
求出 γ
值就行了。
(13－29)是旋转设计的必要条件，满足非退化条件式 (13－30)是使旋
转性成为可能的充分条件。两者结合起来才能使旋转性设计得以实现
。实际操作上主要借助于组合设计来实现。因为组合设计中 N 个试验
点 N ＝ mc+mγ +m0 ，分布在3个半径不相等的球面上。即
第九章回归旋转试验设计

第九章回归旋转试验设计

9回归旋转试验设计本章要点：主要介绍了回归旋转设计的基本原理、实现条件、组合设计的步骤和统计分析方法，并给出二次回归正交旋转试验设计的计算案例。

重点：回归正交旋转设计的实现条件、组合设计的方法、方程的建立及显著性检验。

难点：回归正交旋转设计正交和旋转的实现条件及其统计分析。

9.1回归旋转试验设计的基本原理前面所介绍的“回归正交设计”，具有试验处理数比较少，计算简便、消除回归系数之间的相关性等优点。

但它也存在一定的缺点，即二次回归预测值的方差随试验点在因子空间的位置不同而呈现较大的差异。

由于误差的干扰，就不易根据预测值寻找最优区域。

为了克服这个缺点，人们通过进一步研究，提出了回归旋转设计（whirly design ）。

所谓旋转性是指试验因素空间中与试验中心距离相等的球面上各处理组合的预测值的方差具有几乎相等的特性，具有这种性质的回归设计称回归旋转设计。

这种设计的意 义在于可以直接比较各处理组合预测值的好坏，从而找出预测值相对优良的区域。

9.1.1回归设计旋转性条件旋转设计包括一次、二次和三次旋转设计，但研究中最常见的设计是二次回归旋转设计。

下面以三元二次回归方程来讨论回归正交的旋转性问题。

二次正交多项式方程的估计值为： 如果以三因素二次回归正交设计的数学模型为例：因此其信息矩阵A 为：T A=x x=ˆy ˆy332011ˆj j ij i j jj jj i jj y b b x b x x b x ===+++∑∑∑2220112233121213132323111222333ˆy b b x b x b x b x x b x x b x x b x b x b x =+++++++++1231213231231121312131231121322222232a a a a a a a a a a a aa a a a a a a a a a a a a a a a a n x x x x x x x x x x x x x x x x x x x x x x x x x x x x x ∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑223121232312223312313231322222322222a a a a a a a a a a a a a a a a a a a a a a a a a x x x x x x x x x x x x x x x x x x x x x x x x x ∑∑∑∑∑∑∑∑∑∑∑∑∑ 对233121231231212123232222332a a a a a a a a a a a a a a a a a a x x x x x x x x x x x x x x x x x x∑∑∑∑∑∑∑∑∑称13123131231323123232322232322233a a a a a a a a a a a a a a a a a a a a a x x x x x x x x x x x x x x x x x x x x x ∑∑∑∑∑∑∑∑∑ 1121342222a a a a a x x x x x ∑∑∑ 部223422a a a x x x ∑∑ 分34a x ⎛⎫ ⎪ ⎪ ⎪ ⎪⎪ ⎪⎪⎪ ⎪ ⎪ ⎪⎪ ⎪⎪ ⎪⎪⎪ ⎝⎭∑上述信息矩阵中的各个元素可用一般形式表达为： ，其中x 的指数1Q 、2Q 、3Q 分别可取0、1、2、3、4等非负整数。

回归通用旋转设计的几个问题_卢恩双


-
1 20 23- 3 B 0+ B 22+ ( B 11+ B 22 )。 10 160 160 除了回归系数计算不一样以外 , 回归方程及回
归系数的显著性检验也不同。 在回归正交设计和正 交旋转设计中都是直接先求回归平方和 , 然后求剩
剩 = SS T - U , S ST 为总平方和 ) , 而在通 余平方和 ( Q n p
- 1 2
112
2
西北农林科技大学学报 (自然科学版 )
第 30卷
播种 , 小区面积为 13. 34 m , 锄地 4 次 , 1991-10-10 收 获 , 单收 单 打 , 风 干称 重 , 大 豆 生 育 期降 雨 390. 3 mm , 前期降雨偏多 , 后期旱象严重 ,生育期积
温为 3 349 ℃ , 试验 安 排及 试 验结 果 见参 考 文 献 [ 3 ]。
第 5期 z0 1 1 1 1 1 X 2= 1 1 1 1 1 1 1 1
n
卢恩双等 : 回归通用旋转设计的几个问题 z1 1 1 - 1 - 1 1. 414 - 1. 414 0 0 0 0 0 0 0 z2 1 - 1 - 1 1 0 0 1. 414 - 1. 414 0 0 0 0 0 z 1z 2 1 - 1 - 1 1 0 0 0 0 0 0 0 0 0 z1 1 1 1 1 2 2 0 0 0 0 0 0 0
′
z2
′
1 2 3 4
0. 5 0. 5 0. 5 0. 5 1. 5 1. 5 - 0. 5 - 0. 5
0. 5 0. 5 0. 5 0. 5
- 0. 5 5 - 0. 5 6 1. 5 1. 5 7 8
- 0. 5 - 0. 5 9 - 0. 5 - 0. 5 10 - 0. 5 - 0. 5 11 - 0. 5 - 0. 5 12 - 0. 5 - 0. 5 13 - 0. 5 - 0. 5 14 - 0. 5 - 0. 5 15 - 0. 5 - 0. 5 16

第9讲 回旋转设计

第九讲 回归旋转设计分析方法REGRESSION ROTATABLE DESIGN回归旋转设计是在回归正交设计的基础上发展而来的。

但后者的预测值Yˆ的方差很大程度上依赖于试验点在因子空间的位置。

由于误差的干扰，试验不能根据预测值直接寻找最优区域。

若使用二次设计具有旋转性，便能使与试验中心点距离相等的试验点上的预测值方差相等。

将有助于克服回归正交设计的不足。

故此，本讲着重讨论二次回归旋转设计及分析。

第一节 二次通用旋转设计的方法一、试验点的确定二次旋转设计也是一种组合设计（为克服试验规模过于庞大，在因素空间中选择n 类具有不同特点的点，把它们适当组合起来而形成试验计划）。

它的试验处理数目N 由三部分组成，即：N=m c +2P +m 0 （9—1）其中：m c 为所选用正交表中的全试验数；p 为试验因素的个数；m 0为各因素零水平组成的中心试验点的重复数。

N 个试验点是分布在三个半径不相等的球面上。

其中m c 个点分布在半径p c =p 的球面上；2p 个点分布在半径p γ=γ的球面上；m 0个点集中在半径p 0=0的球面上。

因此，它满足了旋转性和非退化性。

有关m 0的重复次数，二次旋转组合设计对m 0的选择是自由的，即使中心点的试验一次也不做，也不会影响旋转性，但中心点附近区域往往是我们所关心的区域，而且中心点重复试验能给出回归方程在中心点的拟合情况。

所以，中心点m 0的重复试验是很有必要的。

m 0因p 不同而不同。

现将通用旋转设计的一些有关参数列于表9—1，供设计时查用。

表9—1 二次通用旋转设计的参数表表9—1中γ值可按下式计算)4(2ip -=γ(9—2)式中：p 为因素个数；i 为实施情况，当试验全实施时i=0，1/2实施时i=1；1/4实施时i=2。

二、二次旋转计划的安排设为研究的因素有p 个，分别以Z 1、Z 2、…、Zp 表示，每因素的上水平为Z i2，下水平为Z i1，零水平为Z i0，变动区间（Δi ）为：)39(2210-+=i i i Z Z Z△)49(12--=γi i i Z Z其中r 值可按p 的个数及实施情况查表9—1或按9—2式计算，然后编制因素水平的编码表9—2。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2 i 2 j
x
i，j =1，2„P；
待定参数
以上为 P 元二次回归旋转设计的旋转性条件。
此外，为了使旋转设计成为可能，还必须使信
息矩阵 A 不退化，为此，必须有不等式：
4 p 2 2 P 2
上式为 P 元二次回归的非退化条件。 已证明，只要使 N 个试验点不在同一个球面上， 就能满足非退化条件。或者说只要使 N 个试验点至少 分布于两个半径不等的球面上，就有可能获得旋转设
P 2 2 ˆ D y P 2 4 PN
4 1 2 P 1 4 P 1 4 1 2 2 4 P 2 4 4
（4.11） 由式（4.11）经研究表明，只有采用恰当的方法 确定 4 ，才能满足通用性的要求。如何确定 4 ？对 4 有什么要求呢？总的来说，它必须使上式中 i处的
ˆ 的 二次旋转组合设计具有同一球面预测值 y
方差相等的优点，但回归统计数的计算较繁琐，
若使它获得正交性就能简化计算手续。
在二次旋转组合计划中，一次项和交互项的 回归系数 bj ，bij 仍保持正交，但 b0 与 bjj 之间，
以及 bii 与 bjj 之间都存在相关，即不具正交性，
它们之间的相关矩分别为：
计方案。
为了获得 P 元二次旋转设计方案，就要求既要
满足非退化条件式，又要满足旋转性条件式。
如何才能满足这两方面的条件呢？这主要借助
于组合设计来实现，因为组合设计中 N 个试验点：
N mc m m0
分布在三个半径不相等的球面上：
mc 个点分布在半径为 P 的球面上； c m 个点分布在半径为 的球面上； m0 个点分布在半径为 0 0 的球面上；
第二节 二次正交旋转组合设计及其统计分析
一、二次正交旋转组合设计的一般方法
设某试验需研究 P 个因素，分别以 Z1, Z2 , …
ZP 表示，在进行设计时，首先拟定每个因素的上下
水平，上水平以 Z2j 表示，下水平以 Z1j 表示（j = 1, 2, …P），再由每个元素的上下水平计算零水平和变 化间距。
二、二次旋转组合设计的通用性
所谓“通用性”，就是试验计划除了仍保持 其旋转性之外，还具有各试验点与中心点的距离 在因子空间编码值 0 ～ 1 的范围内，其预测值
的方差基本相等的性质，即同时具有旋转性与通
用性，这种设计称为通用旋转组合设计。
如何才能满足其通用性呢？我们首先从预测值 y ˆ 的 方差出发讨论：
-1
Z 01 Z 01 1 Z 11
Z2 Z 22 Z 02 2 Z 02 Z 02 2

Z 12

ZP Z 2P Z 0 P P Z 0P Z 0 P P Z 1P
值与 0 处的值相差的平方和为最小。
即:
Q4 f 4 f 1 4 f 2 4
2 0 n i 1 2 i

4 i
最小
2
（4.12） 式中：
P2 f 0 4 P 24 PN 4
P 14 P 1 f 2 4 2 2 4 P 2
变换，以实现其编码。
X j (Z j Z 0 j ) j
（4.15）
这样，就将有量纲的自变量 Zj (j=1,2,…P) 变成 无量纲的规范变量 Xj (j =1, 2,…P) ，则可编制如下的 因素水平编码值表。
表4-3 因素水平编码值表
X

+1 0
Z1 Z 21 Z 01 1
4
P
解此方程，即可建立全实施时 即：

值的计算式，
2P / 4
当
当 当
mc 2 mc 2 mc 2
P （ 1 1/2实施） P 2
2
( P 1) / 4 ( P 2) / 4
（1/4实施） （1/8实施）
2
P 3
2
( P 3) / 4
一、正交性的获得
α的含义：试验点从第1个到第N个
信息矩阵A中的所有元素，可以用以下形式表示：
x
a1 a2 1 2
x
上式中 x 指数a1、a2 可分别取0、1、2、3、4 等数，但它们的和不超过 4 ，即
0 a1 a2 4
信息矩阵A中的元素可以分成两类：
第一类元素，它们的所有指数 a1、a2中至少 有一个为奇数；
x 2
x1x 2
2 x 1x 2 2 x x 1 2 2 2 x 1x 2
2 x 1 2 x 1x 2 3 x 1x 2 4 x 1 3 x 1
2 x 2 2 x1x 2 3 x 2 3 x x 1 2 2 2 x1x 2 4 x 2
某因素的零水平以 Z0j 表示，其计算式为：
Z 0 j Z 2 j Z 1 j 2
（4.13）
某因素的变化间距以 j 表示，其计算式为：
j Z 2 j Z 0 j
（4.14）
式中 γ 为待定参数，其值可以从表4-1中查出。
对每个因素 Zj 各水平的取值进行如下的线性
x
a
2 2 i j
x mc
均不等于零，完全符合旋转性条件的要求， 为了获得旋转设计方案，还必须根据旋转性条 件确定

值，事实上只要使：
事实上只要使：
x
P
4 j
3 x x
2 2 i j
求出

就可以了。在组合设计下，当
mc 2 P
（全实施），则上式变为：
2 2 3 2
m0 N mc m
计算出不同 P 值的 m0，上述计算结果列于下表:
表4-2 二次通用旋转组合设计参数表
P
2 3 4 5（1/2实施） 6（1/2实施） 7（1/2实施） 8（1/2实施） 8（1/4实施） 4 8 16 16 32 64 128 64
mc m
4 6 8 10 12 14 16 16
2 2 Y 0 1 X 1 2 X 2 12 X 1 X 2 11 X X 1 22 2 2 ˆ b0 b1 x1 b2 x2 b12 x1 x2 b11x12 b22 x2 y
它的结构矩阵为：
1 x11 1 x21 X 1 x N1

1.414 1.682 2.000 2.000 2.378 2.828 3.364 3.828
0.81 0.86 0.86 0.89 0.90 0.92 0.93 0.93
4
N 13 20 31 32 53 92 165 93
m0
5 6 7 6 9 14 21 13
从上述讨论结果看出，为了满足通用性要求， 主要在于确定出适当的 m0 ,因此，只要在中心点安 排如上表所列的 m0 次试验，即可使二次旋转组合 设计获得通用性。
x12 x22 xN 2
x11x12 x21x22 xN 1 xN 2
x x
2 11 2 21

2 xN 1
x x 2 xN 2
2 12 2 22
A X X 1 x11 x 12 X x11x12 x2 11 x2 12
cov(b0 , b jj ) 224t 2 / N cov(bii , b jj ) ( 4 )t / N
2 2 2
要使二次回归旋转组合设计获得正交性，就 需消除相关性，消除 b0 与 bjj 之间的相关性，只
需对平方项施行中心化变换，即
1 2 j X j X N
使二次旋转组合设计具有一定正交性。
表4-1 二次正交旋转组合设计参数表
P
2（全实施） 3（全实施） 4（全实施） 4（1/2实施） 5（全实施） 5（1/2实施） 6（1/2实施） 6（1/4实施） 7（1/2实施） 7（1/4实施） 8（1/2实施） 8（1/4实施） 8（1/8实施） 4 8 16 8 32 16 32 16 64 32 128 64 32
mc
m
4 6 8 8 10 10 12 12 14 14 16 16 16
m0
8 9 12 7 17 10 15 8 22 13 33 20 11
N 16 23 36 23 59 36 59 36 100 59 177 100 59

1.414 1.682 2.000 1.682 2.378 2.000 2.378 2.000 2.828 2.378 3.364 2.828 2.374
第四章
回归的正交设计
回归的旋转设计
优点：试验处理比较少，计算简便， 消除了回归系数之间的相关性。
缺点：即二次回归预测值 y ˆ 的方差， 随试验点在因子空间的位置不同而呈现较 大的差异，由于误差的干扰，就不容易根 据预测值寻找最优区域。 回归的旋转设计是为了克服上述缺点而提出的。
第一节 旋转设计的基本原理 Rotary design
因此，采用组合设计选取的试验点， 完全能够满足非退化条件。 此外，采用组合设计，其信息矩阵
A 的元素中：
2 2 x x x x j i j i xj 0 a


这就满足旋转性条件式，而它的偶次方元素：
2 2 x m 2 i c 4 4 x m 2 i c a a
2 X j i 1
N
平方项之间相关性的消除，需使
cov(bii , b jj ) ( 4 )t / N 式中
2 2 2
4 2 2
或者 / 2 1 就会使 4 2
cov( bii , b jj ) 0