非线性动力学-2讲解
- 格式:ppt
- 大小:1.71 MB
- 文档页数:8



非线性动力学的理论与应用第一章介绍非线性动力学(Nonlinear Dynamics)是指研究非线性系统运动的学科,与传统的线性动力学不同,它所研究的系统是依赖于初始条件及过程中反馈、耗散及非线性耦合等的状态变化规律。
非线性动力学模型可以是连续的,也可以是离散的,涉及到许多数学工具,包括微积分、常微分方程、偏微分方程、拓扑学、代数几何等。
第二章研究内容非线性动力学研究的主要内容是非线性动力系统在自然界、生产生活和科学技术中的应用和理论。
这里说的非线性动力系统,主要指具有非线性特性的动力系统,包括天气气候预测、生物学、生物医学、材料科学、航空航天等等各个领域的动力学系统。
1.混沌理论混沌理论是非线性动力学中的核心之一,也是最吸引人的方向之一。
混沌现象是随着时间推进,系统状态的巨大变化,这是由于微小的初始条件的微小变化而引起的。
混沌现象最早是由美国数学家李雅普诺夫(A.N.Kolmogorov)提出的,其主要特点是系统的轨迹看似毫无规律可寻,在函数中体现出一些随机的性质。
2.非周期振荡非周期振荡是非线性动力学的另一个重要方向。
它是指系统为适应外部环境和内部自身反馈机制作出的一种非线性动态的运动状态。
非周期振荡可以被看作是一种自适应的机制,可以在动态环境中寻找到对稳定性更好的点,也可以用于刻画非线性振动系统的动态特性。
3.射影演化动力学射影演化动力学是指在相空间上进行射影变换,通过将相空间上的点映射到下一时刻的点来描述系统的真实运行情况。
射影动力学模型的研究主要涉及轨道的几何特征和混沌现象的显现。
第三章应用非线性动力学在实际中有广泛的应用场景,其主要应用包括:1.天气气候预测天气气象研究是非线性动力学应用的早期领域之一。
天气系统本身包含着复杂的非线性特性,可以用非线性动力学方法来研究气象系统的稳定性和不稳定性,进而提高天气预报的精度。
2.生物学研究在生物学中,非线性动力学在神经生理学、心理学、进化生物学、群体生物学、生态学等方面都有很重要的应用,可以帮助揭示复杂的生物系统中的动态机制和交互关系。



即non-linear 是指输出输入既不是正比例也不是反比例的情形。
如宇宙形成初的混沌状态。
自变量与变量之间不成线性关系,成曲线或抛物线关系或不能定量,这种关系叫非线性关系。
“线性”与“非线性”,常用于区别函数y = f (x)对自变量x的依赖关系。
线性函数即一次函数,其图像为一条直线。
其它函数则为非线性函数,其图像不是直线。
线性,指量与量之间按比例、成直线的关系,在空间和时间上代表规则和光滑的运动;而非线性则指不按比例、不成直线的关系,代表不规则的运动和突变。
如问:两个眼睛的视敏度是一个眼睛的几倍?很容易想到的是两倍,可实际是 6-10倍!这就是非线性:1+1不等于2。
非线性关系虽然千变万化,但还是具有某些不同于线性关系的共性。
线性关系是互不相干的独立关系,而非线性则是相互作用,而正是这种相互作用,使得整体不再是简单地等于部分之和,而可能出现不同于"线性叠加"的增益或亏损。
激光的生成就是非线性的!当外加电压较小时,激光器犹如普通电灯,光向四面八方散射;而当外加电压达到某一定值时,会突然出现一种全新现象:受激原子好像听到“向右看齐”的命令,发射出相位和方向都一致的单色光,就是激光。
迄今为止,对非线性的概念、非线性的性质,并没有清晰的、完整的认识,对其哲学意义也没有充分地开掘。
线性:从相互关联的两个角度来界定,其一:叠加原理成立;其二:物理变量间的函数关系是直线,变量间的变化率是恒量。
在明确了线性的含义后,相应地非线性概念就易于界定:其—,“定义非线性算符N(φ)为对一些a、b或φ、ψ不满足L(aφ+bψ)=aL(φ)+bL(ψ)的算符”,即叠加原理不成立,这意味着φ与ψ间存在着耦合,对(aφ+bψ)的*作,等于分别对φ和ψ*作外,再加上对φ与ψ的交叉项(耦合项)的*作,或者φ、ψ是不连续(有突变或断裂)、不可微(有折点)的。
其二,作为等价的另—种表述,我们可以从另一个角度来理解非线性:在用于描述—个系统的一套确定的物理变量中,一个系统的—个变量最初的变化所造成的此变量或其它变量的相应变化是不成比例的,换言之,变量间的变化率不是恒量,函数的斜率在其定义域中有不存在或不相等的地方,概括地说,就是物理变量间的一级增量关系在变量的定义域内是不对称的。

非线性动力学原理及应用随着科学技术的不断发展,非线性动力学已经成为研究各种现象的一种重要方法。
这种方法不仅能够帮助人们更好地理解自然现象,还可以应用到很多领域中。
本文将介绍非线性动力学的基本原理以及它的应用。
什么是非线性动力学?非线性动力学是一种描述非线性系统特征的方法,可以用来研究类似于混沌现象的一些现象。
在非线性动力学中,系统的状态是由一组微分方程来描述的。
这些微分方程的解决方案非常复杂,可能会显示出周期性或无规律的变化。
这种不规则的变化就是混沌所表现出的特征之一。
非线性动力学的应用非线性动力学有着广泛的应用,可以用于很多领域中,以下是其中的几个例子:1、天气预测天气系统是一个典型的非线性系统,其中包含许多不同的因素,如湍流、大气压力、温度、湿度等等。
由于这些因素之间的相互作用比较复杂,根本无法通过简单的线性模型来描述气象现象,因此需要使用非线性动力学方法来进行预测。
2、经济系统经济系统也是一个具有非线性特征的系统。
由于经济活动中涉及到太多的因素,比如价格、货币供应量、利率、税务政策等等,使得经济系统具有不确定的变化和波动性。
使用非线性动力学方法可以更好地理解经济现象,并对未来情况进行预测。
3、生物学研究在生物学领域中,非线性动力学可以用于研究生物系统中的一些现象,比如心脏跳动、神经元在脑中的传递等等。
由于这些现象中涉及到很多的变量和相互作用,因此需要使用非线性动力学方法来处理这些复杂的系统。
总体来说,非线性动力学方法可以用于研究各种不规则的现象,并可以为科学家提供更深入的理解和预测,从而进一步推动科学技术的发展。
总结非线性动力学提供了一种用微分方程来描述和分析复杂系统的方法。
这种方法不仅可以为科学家提供更深入的理解和预测,还可以用于很多领域,如天气预测、经济、生物学等等。
虽然这种方法的应用范围很广,但也有一些问题需要解决,比如系统的精度、数据的质量等等。
通过不断的改进和创新,相信非线性动力学方法将会在更多领域得到应用。


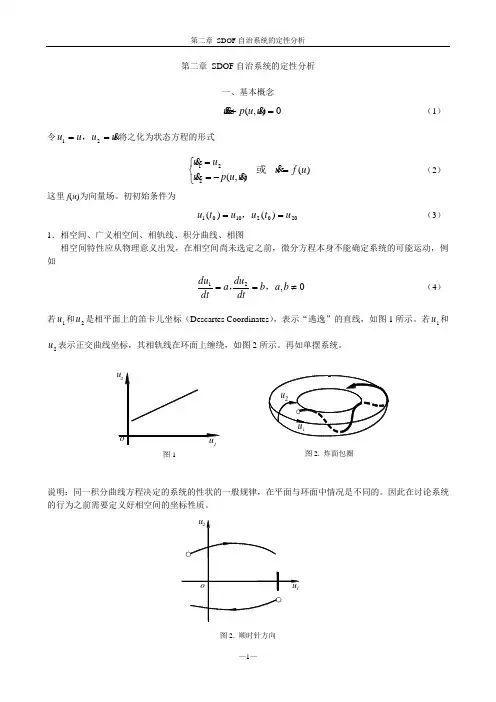
第二章 SDOF 自治系统的定性分析一、基本概念0),(=+u u p u(1)令uu u u ==21,将之化为状态方程的形式 )(),(221u f u u u p uu u=⎩⎨⎧-== 或 (2)这里f (u )为向量场。
初初始条件为20021001)()(u t u u t u ==,(3)1.相空间、广义相空间、相轨线、积分曲线、相图相空间特性应从物理意义出发,在相空间尚未选定之前,微分方程本身不能确定系统的可能运动,例如21dudu ,相图特点:(1)上半平面,021>=u u ,相轨线从左到右;(2)下半平面,021<=u u,相轨线从左到右;(3)横坐标,∞→⎪⎪⎭⎫⎝⎛=0122u du du ,轨线与横轴正交。
2.定理:若),;(00u t t u u= 是方程(2)的解,对任意常数0t ,),0;(00u t t u u -= 仍是其解。
证明:对任何时刻/t ,有()()///|)()(|)(|)(00/0t t t t t t t t t u f t t u f dtt du dt t t du =-==-=-==- (5)表明:上式在任意瞬时恒成立,故),0;(00u t t u u-= 是解。
说明:自治系统在相空间的轨线只与初始值有关,与初始时刻的选取无关。
因此,今后令00=t ,初始条件(3)成为2010)0()0(u u u u ==,(6)例1:对自治系统0=+u u,t u sin =是其解,)sin(0t t u -=还是其解。
若取t u cos -=,此时20π=t 。
推论:经过相空间中的每一点(奇点除外),自治系统有一条且仅有一条相轨线(只有唯一轨线通过)。
证明:设方程(2)有两条轨线),,(1010u t t u u =,),,(2020u t t u u =有公共点,即在时刻1T 和2T 有),,(),,(2020210101u t T u u t T u =(7)因),,(101021u t T T t u u -+=还是方程(2)的解,因此下式成立22|),,(|),,(2020101021T t T t u t t u u t T T t u ===-+(8)根据Cauchy 定理:若在),(00u t 的邻域f 对u 的偏导数存在并连续,对t 的单边偏导数存在并连续,则),(u t f u = 在相当小的区间],0[δ内存在唯一解(过同一初始值的解是唯一的)。
非线性动力学的基本原理和应用实例非线性动力学,又称为混沌理论,是一门研究复杂系统行为的学科。
它研究的领域包括物理学、化学、生物学、社会学等多个领域。
本文将介绍非线性动力学的基本原理和应用实例。
一、非线性动力学的基本原理非线性动力学研究的是具有非线性行为的系统。
所谓非线性行为,指的是系统对初始条件的微小变化极其敏感,这种敏感性在系统中表现为不可预测性和不规则性。
一个非线性系统可以用微分方程的形式表示。
因此,非线性动力学的基本原理是微分方程的求解。
非线性系统的微分方程通常较为复杂,无法通过解析方法求解。
因此,在非线性动力学中,常常使用数值计算方法来模拟系统的行为。
另一个非线性动力学的基本原理是混沌理论。
混沌理论表明,在一些非线性系统中,微小的扰动可以引起系统行为的剧烈变化。
这是由于在非线性系统中,不同的初值条件会引起系统的行为非常不同。
这种不确定性被称为“混沌”。
二、非线性动力学的应用实例1. 布朗运动布朗运动是指在液体中漂浮的物质在水分子的撞击下不断做无规则的运动。
这个过程可以用随机游走模型来描述,也可以用布朗粒子模型来描述。
布朗粒子模型是一个非线性系统,在模拟过程中需要使用非线性动力学的方法。
布朗运动在化学动力学、生物化学、统计物理学等领域有广泛应用。
2. 汇流问题汇流问题是指在不同流域中通过河道流动的水汇合到同一个点的问题。
这个问题可以用非线性水力模型来描述。
非线性水力模型是一个非线性系统,在模拟过程中需要使用非线性动力学的方法。
汇流问题在水文学和水资源管理等领域有广泛应用。
3. 神经网络神经网络是一种模拟大脑神经元之间相互作用的数学模型。
神经网络可以看作是一个非线性系统,因为神经元之间的连接是多样的、强弱不一的。
用非线性动力学的方法可以对神经网络模型进行仿真和分析。
神经网络在人工智能、模式识别等领域有广泛应用。
4. 生态系统生态系统是指生物体之间以及生物体与周围环境之间相互作用形成的系统。
生态系统通常是非线性的,因为生物体之间的相互作用和生物体与环境之间的相互作用都是非线性的。
非线性动力学的基本概念与原理随着科技的不断发展,物理学等领域也在不断的深入研究。
非线性动力学作为其中一个分支,正逐渐受到人们的关注。
本文就来探讨一下非线性动力学的基本概念与原理。
一、什么是非线性动力学非线性动力学是指研究系统的运动规律与演变过程的学科,它关注的是系统在不同状态下的演化和转化,以及其中的规律性和混沌性等。
非线性动力学最初是由Poincare在竞赛中研究和发现,它和线性动力学不同,线性动力学的系统遵循着线性守恒定律,其状态随时间呈现出稳定的周期振动。
而非线性动力学的系统则会存在不稳定、混沌等问题。
二、非线性动力学的原理非线性动力学的研究涉及到的内容很广泛,包括了力学、物理、生物、化学等多个领域。
其中,非线性动力学的基本原理主要有以下几个方面:1. 非线性系统非线性系统指的是系统中存在着不同程度的非线性关系,常常会出现不可预测的现象。
非线性动力学所研究的系统大多数是非线性系统。
2. 混沌混沌是非线性系统中十分特殊的一种状态,其表现为在一定的参数条件下,系统与初始条件有很大的敏感性,从而使得系统呈现出不规则、复杂的运动状态。
混沌状态包括了自相似、自组织凝聚等自适应现象。
混沌现象的研究对于改变系统的状态具有十分重要的意义。
3. 红外、紫外发散非线性动力学研究中出现的红外、紫外发散问题,是指在计算中出现的无限大结果,其存在导致计算的结果并不精确。
红外、紫外发散问题是非线性动力学中非常常见的问题之一,也是研究非线性动力学的一个难点。
4. 动力学方程动力学方程是非线性动力学中最重要的基础之一,它是描述系统动力学过程的基本工具,也是研究系统演化的数学模型。
动力学方程可以通过数学计算来得到系统运动的轨迹和演化规律,因此其研究对于了解非线性动力学系统的运动规律是必不可少的。
5. 常微分方程常微分方程是非线性动力学中应用最为广泛的数学工具之一,它描述了一些时间变化连续的系统,可用于描述许多非线性动力学系统的演化规律。