04-1zf_两自由度系统的振动

二自由度系统的振动1.概述在实际工程中，真正的单自由度振动是很少的，而是根据需要将被研究对象简化成单自由度系统来研究。

但是许多问题不能简化为单自由度系统，为满足工程精度上的需要，必须按多自由度系统来研究。

一般讲，三自由度以上的系统要得到闭合解是相当困难的。

在这种情况下，可以用坐标变换的方法，将描述实际问题的广义坐标用一组新的坐标来代替。

新坐标所描述的系统运动方程与实际系统是相同的，但用新坐标描述的系统微分方程之间已不存在耦合，称为各自独立的微分方程，就可以按单自由度系统的微分方程那样一一单独求解。

这种新坐标主坐标或模态坐标。

二自由度系统是最简单的多自由度振动系统，许多多自由度喜用的物理概念及解题思路可以从二自由度系统的分析中得到启迪，也是分析多自由度系统的基础。

二自由度振动系统的结构具有两个固有频率。

当系统按其中某一固有频率作自由振动时，称之为主振动。

主振动是简谐振动。

当发生主振动时，描述振动的两个独立变量与振幅之间有确定的比例关系，即两个振幅比决定了整个系统的振动形态，称之为主振型。

任意初始条件下的自由振动一般是这两个不同频率的主振动的叠加，其叠加后的振动不一定是简谐振动。

当外界激扰为简谐激扰时，系统对其响应是与激扰频率相同的简谐振动。

当激扰频率接近系统的任意一固有频率时，就会发生共振。

共振时的振型就是与固有频率相对应的主振型。

此时，喜用的两个振动的振幅都趋于最大值。

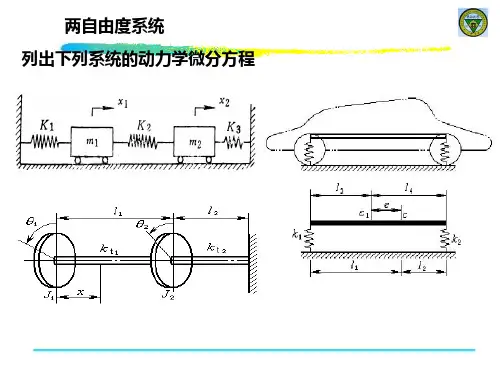
2.二自由度系统的运动方程图1所示为具有粘性阻尼的二自由度系统。

图1.二自由度系统模型对质量m1、m2绘分离体图，如图2所示。

图2.二自由度系统分析图用牛顿第二定律分别列分离体在水平方向方程得：整理得：由两个联立二阶常微分方程所描述的系统统称为二自由度系统。

上述方程可以方便的表示成矩阵形式。

常数矩阵[m]、[c]和[k]分别为质量、阻尼、刚度矩阵。

{x(t)}和{F(t)}分别称为二维位移向量和力向量。

可以将上述方程写成矩阵形式：对于同一系统当采用不同的独立坐标系来描述时，其[m]、[c]、[k]矩阵中的元素是不同的，但不影响系统的固有特性，系统的固有频率与坐标的选取无关，一定的系统固有频率是一定的。

第四章 两自由度系统的振动前两章介绍了单自由度系统的振动，它是振动理论的基础，并有重要的应用价值。

但工程中许多实际问题是不能简化为单自由度系统的振动问题，它们往往需要简化成为多自由度系统。

两自由度系统是最简单的多自由度系统，无论是模型的简化、振动微分方程的建立和求解的一般方法，以及系统响应表现出来的振动特性等等。

两自由度系统和多自由度系统没有本质上的差别，而主要是量上的差别，因此研究两自由度系统是分析多自由度系统振动特性的基础。

所谓两自由度系统是指要用两个独立坐标才能确定系统在振动过程中任何瞬时的几何位置的振动系统。

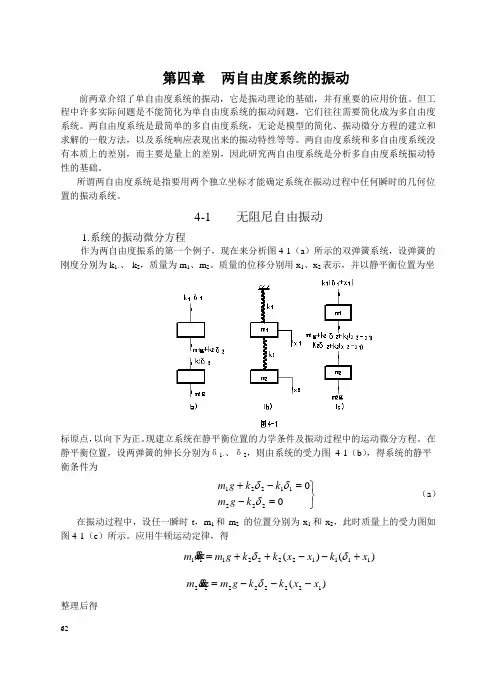
4-1 无阻尼自由振动1.系统的振动微分方程作为两自由度振系的第一个例子，现在来分析图4-1（a ）所示的双弹簧系统，设弹簧的刚度分别为k 1、、 k 2，质量为m 1、m 2。

质量的位移分别用x 1、x 2表示，并以静平衡位置为坐标原点，以向下为正。

现建立系统在静平衡位置的力学条件及振动过程中的运动微分方程。

在静平衡位置，设两弹簧的伸长分别为δ1、、δ2，则由系统的受力图 4-1（b ），得系统的静平衡条件为⎭⎬⎫=-=-+0022211221δδδk g m k k g m （a ）在振动过程中，设任一瞬时t ，m 1和m 2 的位置分别为x 1和x 2，此时质量上的受力图如图4-1（c ）所示。

应用牛顿运动定律，得)()(11112222111x k x x k k g m x m +--++=δδ )(12222222x x k k g m xm ---=δ 整理后得222122222112212212111)(δδδk g m x k x k x m k k g m x k x k k xm -=-+-+=-++ } （b ）将方程（b ）的右端和方程(a)比较，就可以消去平衡项，于是得00)(1222222212111=-+=-++x k x k xm x k x k k xm } (4-1)令 ,/,/,/)(2222121m k c m k b m k k a ==+=则（4-1）式可改写成00122211=-+=-+cx cx xbx ax x } (4-2)这是联立的二阶常系数线性微分方程组。

第四章两自由度系统的振动介绍第四章是关于两自由度系统的振动的介绍。

在这一章中，我们将探讨两自由度系统的振动模型、动力学方程，并讨论其解析解和数值解。

此外，我们还将介绍两自由度系统的模态分析、共振现象以及一些相关的应用。

两自由度系统是一种具有两个自由度的振动系统，它由两个具有质量和弹性的物体通过柔性连接件或刚性连接件相互连接而成。

这些物体可以是质点、弹性体或刚体等，而连接件可以是弹性杆、弹簧、细梁等。

在两自由度系统中，每个物体都可以做平动或转动运动，因此系统具有两个自由度。

例如，双摆锤、双弹簧振子等都属于两自由度系统。

两自由度系统的动力学方程可以由拉格朗日方程或牛顿第二定律得到。

得到动力学方程后，我们可以通过解方程得到系统的解析解，以获得系统的振动特性。

在分析解时，通常要求系统的运动是简谐振动或近似简谐振动。

另一种求解两自由度系统的方法是数值解法。

数值解法可以通过数值积分来近似求解动力学方程，这种方法常用于求解复杂的系统，或者对系统参数进行优化等情况。

分析解和数值解法可以用来研究两自由度系统的固有振动频率、振型和动态响应等。

通过模态分析，我们可以得到系统的固有频率，并确定每个模态的振型。

对于实际工程问题，模态分析可以帮助我们了解系统的共振情况，并设计出合适的控制策略，以求减小共振现象的发生。

共振是两自由度系统中一个重要而常见的振动现象。

当外力的频率与系统的固有频率接近时，系统会发生共振现象。

共振的发生会导致系统振幅的急剧增加，并且可能对系统的稳定性产生不利影响。

因此，在设计过程中，需要避免共振现象的发生，并采取合适的措施来控制共振。

此外，两自由度系统的振动也有许多实际应用。

例如，双摆锤可以用来研究天体运动和天文学现象；双弹簧振子可以用来研究建筑物或桥梁的振动特性；双振子可以用来研究分子振动和分子动力学等。

总而言之，两自由度系统的振动是一种普遍且重要的物理现象。

通过对两自由度系统进行建模和分析，我们可以深入了解系统的振动特性，并在实际应用中进行优化和改进。

两自由度系统振动规律《探索两自由度系统振动规律：一场奇妙的科学之旅》嗨，大家好！今天我想跟你们讲讲特别有趣的两自由度系统振动规律。

你们有没有想过，这个世界上有好多东西都会振动呢？就像我们学校的秋千，荡来荡去的，那就是一种振动。

不过呀，两自由度系统的振动可比秋千复杂多啦。

我先给你们讲个故事吧。

我们班上有个小发明家，叫小明。

有一天，他带来了一个他自己做的小玩意儿，是用两根弹簧和两个小木块组成的。

他说这就是一个简单的两自由度系统模型。

当时我们都围了过去，好奇得不得了。

我就问小明：“这东西咋就能体现两自由度系统振动规律呢？看着就像两个小木块被弹簧连着，好像没什么特别的呀。

”小明笑着说：“你们可别小看它。

这两个小木块，每个都能在自己的方向上运动，这就是两个自由度啦。

”然后呢，小明就开始摆弄这个小模型。

他轻轻地拉了一下其中一个小木块，哇，这时候可有趣了。

那个被拉的小木块就开始动起来了，而且还不是简单地动，另一个小木块也跟着动了起来。

就好像它们两个是好朋友，一个有动作，另一个也跟着有反应。

我当时就觉得好神奇，这就像我们跳舞的时候，领舞的人做了一个动作，旁边配合的人也会跟着做出相应的动作一样。

这时候，我们班的学霸小红说话了：“你们知道吗？这其实就跟两自由度系统振动规律有关。

在这个系统里，每个小木块的振动都不是独立的，它们之间有着一种相互影响的关系。

这就好比我们生活在一个集体里，我们每个人的行为也会影响到周围的人呢。

”我就又问小红：“那这个规律到底是怎么个事儿呀？”小红想了想，说：“嗯，这个两自由度系统的振动啊，就像是一场交响乐。

每个小木块就像一个乐器，它们各自发出自己的声音，但是又要相互配合。

当我们拉动一个小木块的时候，就像是给这个乐器奏响了一个音符，然后这个音符就会通过弹簧这个‘指挥棒’传递到另一个小木块那里，让另一个小木块也开始演奏属于它的旋律。

”我听了小红的话，似懂非懂的。

这时候，小明又补充道：“对呀，而且这个振动还有频率呢。