第七章离散信号与系统的复频域分析(2)L23_CH7.
- 格式:ppt
- 大小:572.50 KB
- 文档页数:5






信息科学与工程学院《信号与系统》实验报告四专业班级电信 09-班姓名学号实验时间 2011 年月日指导教师陈华丽成绩实验名称离散信号的频域分析实验目的1. 掌握离散信号谱分析的方法:序列的傅里叶变换、离散傅里叶级数、离散傅里叶变换、快速傅里叶变换,进一步理解这些变换之间的关系;2. 掌握序列的傅里叶变换、离散傅里叶级数、离散傅里叶变换、快速傅里叶变换的Matlab实现;3. 熟悉FFT算法原理和FFT子程序的应用。
4. 学习用FFT对连续信号和离散信号进行谱分析的方法,了解可能出现的分析误差及其原因,以便在实际中正确应用FFT。
实验内容1.对连续信号)()sin()(0tutAetx taΩα-=(128.444=A,πα250=,πΩ250=)进行理想采样,可得采样序列50)()sin()()(0≤≤==-nnunTAenTxnx nTaΩα。
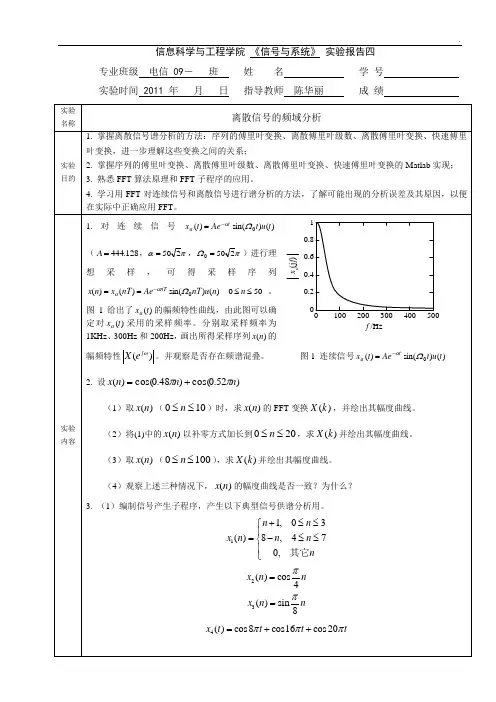
图1给出了)(txa的幅频特性曲线,由此图可以确定对)(txa采用的采样频率。
分别取采样频率为1KHz、300Hz和200Hz,画出所得采样序列)(nx的幅频特性)(ωj eX。
并观察是否存在频谱混叠。
图1 连续信号)()sin()(0tutAetx taΩα-=2. 设)52.0cos()48.0cos()(nnnxππ+=(1)取)(nx(100≤≤n)时,求)(nx的FFT变换)(kX,并绘出其幅度曲线。
(2)将(1)中的)(nx以补零方式加长到200≤≤n,求)(kX并绘出其幅度曲线。
(3)取)(nx(1000≤≤n),求)(kX并绘出其幅度曲线。
(4)观察上述三种情况下,)(nx的幅度曲线是否一致?为什么?3. (1)编制信号产生子程序,产生以下典型信号供谱分析用。
11,03()8,470,n nx n n nn+≤≤⎧⎪=-≤≤⎨⎪⎩其它2()cos4x n nπ=3()sin8x n nπ=4()cos8cos16cos20x t t t tπππ=++10.80.60.40.20100200300400500xa(jf)f /Hz(2)对信号1()x n ,2()x n ,3()x n 进行两次谱分析,FFT 的变换区间N 分别取8和16,观察两次的结果是否一致?为什么?(3)连续信号4()x n 的采样频率64s f Hz =,16,32,64N =。



离散时间系统频域分析离散时间系统的频域分析是研究离散时间信号在频域上的性质和行为的方法。
在离散时间系统频域分析中,使用离散时间傅里叶变换(Discrete Fourier Transform,DFT),来将离散时间信号从时域转换到频域。
通过分析信号在频域上的频谱分布和频谱特性,可以得到离散时间系统的频率响应和频域特性,对信号的频域分布和频率区间进行评估和分析。
离散时间傅里叶变换是时域信号分析的重要工具,它可以将离散时间信号从时域转换到频域。
离散时间傅里叶变换的定义可以表示为:X(k) = Σ[x(n) * exp(-j*2πkn/N)]其中,X(k)是离散时间信号在频域的频谱,x(n)是离散时间信号,N是信号的长度,k是频谱的索引。
离散时间傅里叶变换将时域信号分解成多个频率成分,通过频谱的幅度和相位信息,可以得到信号在频域上的分布情况。
通过离散时间傅里叶变换可以得到离散时间信号的频谱,进而分析信号在频域上的频率响应和频域特性。
频谱可以反映信号在不同频率上的能量分布情况,通过观察频谱的幅度和相位,可以得到信号的频率成分、频带宽度和频率特性等信息。
在离散时间系统频域分析中,常用的分析工具有频谱图、功率谱密度、频率响应等。
频谱图可以将信号的频谱以图形形式展示出来,通过观察频谱图的形状和分布,可以得到信号在频域上的特点。
功率谱密度是指信号在不同频率上的功率分布情况,可以评估信号在不同频率上的能量分布情况。
频率响应是指系统对不同频率信号的响应情况,可以评估系统对不同频率信号的滤波和增益特性。
离散时间系统频域分析的应用包括信号处理、通信系统、控制系统等领域。
在信号处理中,通过频域分析可以对信号进行滤波、去噪、频域变换等操作,提高信号的质量和分析能力。
在通信系统中,通过频域分析可以评估信号传输和接收的性能,并对系统进行优化和改进。
在控制系统中,通过频域分析可以评估系统的稳定性和控制特性,提高系统的响应速度和稳定性。

离散系统的复频域分析专题研讨【目的】(1) 了解系统函数的零、极点分布与系统特性的关系; (2) 培养学生分析与解决实际问题的能力。
【知识点】离散时间线性时不变系统的系统函数与系统特性、系统响应分析【研讨内容】我国市电是电压为220V 、频率为50Hz 的交流电,电气设备经常受到市电以耦合的方式干扰。
在不影响有用信号的情况下,如何去除信号中混入的工频信号(50Hz)干扰?情况1:信号x 1 (t )=s 1(t )+n (t )中有用信号频率为f 1=20Hz 的正弦信号s 1(t )=sin(2πf 1t ),混入频率为50Hz 的工频信号n (t )=0.2sin(100πt )。
现经过采样率f s =500Hz 模数转换器(ADC)通过设计系统H (z )的零极点的方法,滤除50Hz 工频干扰信号n (t )。
情况2:如果x 2(t )=s 1(t )+s 2(t )+n (t ),其中f 2=100Hz 的正弦信号s 2(t )=sin(2πf 2t ),又如何设计零极点滤除工频干扰?1. (*)信号x (t )经过模数转换(A/D)后变成离散信号x [k ],x [k ]的表达式是什么?编写matlab程序产生信号x 1[k ]和x 2[k ]。
[]()k x k x Fs= ()Fs 为抽样频率1[]sin(2*20*)0.2sin(2*50*)x k k k ππ=+2[]sin(2*20*)sin(2*100*)0.2sin(2*50*)x k k k k πππ=++产生信号源程序f1=20;f2=100;Fs=500;k=0:1:Fs; s1=sin(2*pi*f1*k/Fs); s2=sin(2*pi*f2*k/Fs); n=0.2*sin(100*pi*k/Fs); x1=s1+n; x2=s1+s2+n; X1=fft(x1); X2=fft(x2);subplot(2,2,1); stem(k,x1); title('x1ʱÓòͼ') subplot(2,2,3);plot(-250:250,fftshift(abs(X1))) title('x1ƵÓòͼ')subplot(2,2,2); stem(k,x2); title('x2ʱÓòͼ') subplot(2,2,4);plot(-250:250,fftshift(abs(X2))) title('x2ƵÓòͼ')2. (*)离散LTI 系统的零极点与系统函数的关系是什么?11()()()mjj nii z z H z Kz p ==-=-∏∏ 其中z j 为零点,p i 为极点其中||jjj j j j j z z z z eN eψψ-=-=||i i j j i i i z p z p e D e θθ-=-=()()j i j jiN H z Ke Dψθ+∑∑=∏∏|()|jiN H z KD=∏∏由上式可见,当z 接近于零点z j 时,N j 趋向于0,系统函数幅值趋向于0。
离散时间信号和系统的频域分析离散时间信号与系统是研究数字信号与系统的频域分析,其中离散时间信号是对连续时间信号进行采样得到的,而离散时间系统是对连续时间系统进行离散化得到的。
频域分析是对信号与系统在频率域上的特性进行研究和分析。
对于离散时间信号,其离散化的过程是将连续时间信号在时间轴上进行均匀采样,得到指定的采样间隔,得到离散时间序列。
在频域上,其频谱是周期性的,并且频谱是以单位圆为单位周期的。
频域分析的目的是研究离散时间信号在频率域上的特性,包括频谱范围、频率分辨率、功率谱密度等。
离散时间信号的频域分析可以通过离散时间傅里叶变换(DTFT)来实现。
DTFT是信号在频域上的完全变换,将一个离散时间信号映射到一个连续的频率域函数。
DTFT是一个复数函数,表示信号在不同频率上的振幅和相位。
频谱的振幅可以表示信号在该频率上的能量大小,相位可以表示信号在该频率上的相对位置。
除了DTFT之外,还可以使用离散傅里叶变换(DFT)进行频域分析。
DFT是DTFT的一种计算方法,可以将离散时间信号转换为有限的频域信号。
DFT的计算是通过对离散时间信号进行有限长的时间窗口进行采样,并进行频域变换得到的。
DFT的结果是一个离散的频域信号,也称为频谱。
DFT通常使用快速傅里叶变换(FFT)算法来快速计算。
离散时间系统的频域分析主要是通过系统的频率响应函数来实现。
频率响应函数是系统在不同频率上对信号的响应情况的描述。
对于线性时不变系统,其频率响应函数是系统的传递函数的傅里叶变换。
频率响应函数拥有类似信号的频谱特性,可以描述系统对不同频率的信号的增益和相位。
频域分析在离散时间信号与系统中有着广泛的应用。
首先,频域分析可以帮助我们理解信号的频率构成和能量分布情况,有助于对信号进行合理的处理和分析。
其次,频域分析可以快速计算离散时间系统的响应,能够有效地评估系统的性能和稳定性。
此外,频域分析还可以进行滤波器设计、信号压缩、信号重构等应用。
第7章离散时间系统的Z域分析7.1 学习要求(1)深刻理解z变换的定义、收敛域及基本性质,会根据z变换的定义和性质求解一些常用序列的z变换,能求解z反变换,深刻理解z变换与拉普拉斯变换得关系;(2)正确理解z变换的应用条件;(3)能用z域分析分析系统,求离散系统的零状态响应、零输入响应、完全响应、单位样值响应;(4)深刻理解系统的单位样值响应与系统函数H(z)之间的关系,并能用系统函数H(z)求解频率响应函数,能用系统函数的分析系统的稳定性、因果性。
7.2 本章重点(1)z变换(定义、收敛域、性质、反变换、应用);(2)z域分析(求解分析系统);(3)系统的频率响应函数。
7.3 本章的知识结构7.4 本章的内容摘要7.4.1 Z变换(1)定义∑∞-∞=-=n nzn x z X )()( 表示为:)()]([z X n x Z =。
(2)收敛域 1.有限长序列12(),()0,x n n n n x n n ≤≤⎧=⎨⎩其他 (1)当0,021>>n n 时,n 始终为正,收敛条件为0>z ; (2)当0,021<<n n 时,n 始终为负,收敛条件为∞<z ;(3)当0,021><n n 时,n 既取正值,又取负值,收敛条件为∞<<z 0。
2.右边序列11(),()0,x n n n x n n n ≥⎧=⎨<⎩ (1)当01>n 时,n 始终为正,由阿贝尔定理可知,其收敛域为1x R z >,1x R 为最小收敛半径;(2)当01<n 时,)(z X 分解为两项级数的和,第一项为有限长序列,其收敛域为∞<z ;第二项为z 的负幂次级数,由阿贝尔定理可知,其收敛域为1x R z >;取其交集得到该右边序列的收敛域为∞<<z R x 1。
3.左边序列2(),()0,x n n n x n n ≤⎧=⎨⎩其他(1)当02<n ,n 始终为负,收敛域为2x R z <,2x R 为最大收敛半径; (2)当02>n ,)(z X 可分解为两项级数的和,第一项为z 的正幂次级数,根据阿贝尔定理,其收敛域为2x R z <,2x R 为最大收敛半径;第二项为有限长序列,其收敛域为0>z ;取其交集,该左边序列的收敛域为20x R z <<。