第3章 电阻电路的一般分析总结
- 格式:doc
- 大小:177.50 KB
- 文档页数:12

第三章电阻电路的一般分析电路的一般分析是指方程分析法,它是以电路元件的约束特性(VCR)和电路的拓扑约束特性(KCL,KVL)为依据,建立以支路电流或回路电流,或结点电压为变量的回路方程组,从中解出所要求的电流、电压、功率等。
方程分析法的特点是:(1)具有普遍适用性,即无论线性和非线性电路都适用;(2)具有系统性,表现在不改变电路结构,应用KCL,KVL,元件的VCR建立电路变量方程,方程的建立有一套固定不变的步骤和格式,便于编程和用计算机计算。
本章的重点是会用观察电路的方法,熟练运用支路法、回路法和结点电压法的“方程通式”写出支路电流方程、回路方程和结点电压方程,并加以求解。
3-1 在一下两种情况下,画出图示电路的图,并说明其节点数和支路数(1)每个元件作为一条支路处理;(2)电压源(独立或受控)和电阻的串联组合,电流源和电阻的并联组合作为一条支路处理。
解:(1)每个元件作为一条支路处理时,图(a)和(b)所示电路的图分别为题解3-1图(a1)和(b1)。
图(a1)中节点数6b==n,支路数11图(b1)中节点数7=bn,支路数12=(2)电压源和电阻的串联组合,电流源和电阻的并联组合作为一条支路处理时,图(a)和图(b)所示电路的图分别为题解图(a2)和(b2)。
图(a2)中节点数4b=n,支路数8=图(b2)中节点数15b=n,支路数9=3-2指出题3-1中两种情况下,KCL,KVL独立方程数各为多少?解:题3-1中的图(a)电路,在两种情况下,独立的KCL方程数分别为(1)51==4n1--1=6-1-=n (2)3独立的KVL方程数分别为(1)61=84+--n+=1b1=111b (2)5+6+--n=图(b)电路在两种情况下,独立的KCL方程数为(1)61=5-=1n-7n (2)41=1-=-独立的KVL方程数分别为(1)6+1=95b1-n+=-=1271b (2)51=-n++-3-3对题图(a)和(b)所示G,各画出4个不同的树,树支数各为多少?解:一个连通图G 的树T 是这样定义的:(1) T 包含G 的全部结点和部分支路;(2) T 本身是连通的且又不包含回路。


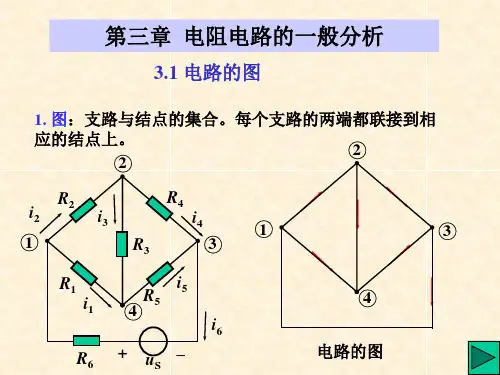
第3章电阻电路的一般分析3.1 复习笔记一、电路图论的基本概念1.图(G)图(G)是具有给定连接关系的结点和支路的集合,其中每条支路的两端都连到相应的结点上,允许孤立结点的存在,没有结点的支路不能称为图。
路径:从G的一个结点出发,依次通过图的支路和结点(每一支路和结点只通过一次),到达另一个结点(或回到原出发点),这种子图称为路径。
连通图:当G的任意两结点都是连通的,称G为连通图。
有向图:赋予支路方向的图称为有向图。
2.树(T)满足下列三个条件的子图,称为G的一棵树:①连通的;②包含G的全部结点;③本身没有回路。
树支与连支:属于树的支路称为树支;不属于树的支路称为连支。
基本回路:对于G的任意一个树,有且只有一条连支回路,这种回路称为单连支回路或基本回路。
树支数:对于有n个结点,b条支路的连通图,树支数=n-1。
推论:连枝数=b-n+1;基本回路数=连支数=b-n+1。
二、KCL和KVL的独立方程数KCL的独立方程数:对一个具有n个结点的电路而言,其中任意的(n-1)个结点的KCL方程是独立的。
KVL的独立方程数:对一个具有n个结点和b条支路的电路而言,其KVL的独立方程数为(b-n+1)。
三、电路的分析方法1.支路电流法(1)支路电流法是以b个支路电流为变量列写b个方程,并直接求解。
其方程的一般形式为(2)支路电流法解题步骤①标出各支路电流的方向;②依据KCL列写(n-1)个独立的结点方程;③选取(b-n+1)个独立回路,标出回路绕行方向,列写KVL方程。
注:①独立结点选择方法:n个结点中去掉一个,其余结点都是独立的;②独立回路选择方法:先确定一个树,再确定单连支回路(基本回路),仅含唯一的连支,其余为树支。
2.网孔电流法(1)网孔是最简单的回路,即不含任何支路的回路。
网孔数=独立回路数=b-n+1。
网孔电流法是以网孔电流为未知量,根据KVL对全部网孔列出方程求解。
(2)网孔电流法解题步骤①局部调整电路,当电路中含有电流源和电阻的并联组合时,可转化为电压源和电阻的串联组合;②选取网孔电流,指定网孔电流的参考方向;③依据KVL列写网孔电流方程,自阻总为正,互阻视流过的网孔电流方向而定,两电路同向取“+”,异向取“-”。







第三章电阻电路的一般分析本章内容:1.电路的图及KCL和KVL独立方程数 2.支路分析法3.网孔分析法4.回路电流法5.结点分析法本章重点:主要学习电阻电路的方程建立及一般分析方法(支路分析法、网孔分析法、节点分析法、回路分析法。
其中,支路分析法是最基本的方法)。
本章难点:独立回路数的确定, 回路分析法及节点分析法.§3-1 电路的图本节介绍有关图论的初步知识,学习应用图的方法选择电路方程的独立变量一、电路的图(G)数学上的图:是边(支路)和顶点(结点)的集合,每一条边都连到相应的顶点上,边是抽象的线段,当移去边时,顶点保留,当移去顶点时,应将顶点所连的支路移走。
1.电路的图(连通图G):是将支路画成的抽象线段形成的节点和支路的集合,结点相对于数学图的顶点,支路相当于数学图中的边。
支路是实体。
KVL和KCL 与元件的性质无关,故可用图讨论其方程。
2.无向图:画出的没有方向的图为无向图3.有向图:画出的有方向的图为有向图4.连通图:任意两个结点之间至少有一条支路或路径时的图为连通图。
二、电路的图的画法(有几种,其中简便的画法)1.一般将电阻和电压源串联的组合,电阻和电流源并联的组合看成一条支路, 将流过同一个电流的每一个分支看成一条支路。
如(b)2.指定电流和电压的参考方向,一般选关联参考方向。
如图(c)(a) (b) (c)§3-2 KCL和KVL的独立方程数一、KCL的独立方程数(n个结点电路,KCL的独立方程是n-1个)将电路的有向图,结点和支路加以编号,如下图,对结点①②③④列写KCL 方程有由于每条支路与两个结点相联,其电流从一个节点流出,从另一个结点流入,一正,一负(从表达式可见),将上面4个方程相加,等式两边为0,说明4个方程不是独立的;将上面3个方程相加,等式两边不为0,说明3个方程是独立的。
可见,n个结点电路,n-1个结点的KCL方程是独立的一、KVL的独立方程数(b条支路,n个结点,KVL为b-(n-1)个)KVL的独立方程数等于独立回路数独立回路数等于基本回路数,回路与支路的方向无关,以无向图讨论。
第三章电阻电路的一般分析一、教学基本要求电路的一般分析是指方程分析法,是以电路元件的约束特性(VCR)和电路的拓补约束特性(KCL、KVL)为依据,建立以支路电流或回路电流或结点电压为变量的电路方程组,解出所求的电压、电流和功率。
方程分析法的特点是:(1)具有普遍适用性,即无论线性和非线性电路都适用;(2)具有系统性,表现在不改变电路结构,应用KCL,KVL,元件的VCR建立电路变量方程,方程的建立有一套固定不变的步骤和格式,便于编程和用计算机计算。
本章学习的内容有:电路的图,KCL和KVL的独立方程数,支路电流法,网孔电流法,回路电流法,结点电压法。
本章内容以基尔霍夫定律为基础。
介绍的支路电流法、回路电流法和节点电压法适用于所有线性电路问题的分析,在后面章节中都要用到。
内容重点:会用观察电路的方法,熟练应用支路电流法,回路电流法,结点电压法的“方程通式”写出支路电流方程,回路电流方程,结点电压方程,并求解。
预习知识:线性代数方程的求解难点:1. 独立回路的确定2. 正确理解每一种方法的依据3. 含独立电流源和受控电流源的电路的回路电流方程的列写4. 含独立电压源和受控电压源的电路的结点电压方程的列写二、学时安排总学时:6三、教学内容§3-1 电路的图1. 网络图论图论是拓扑学的一个分支,是富有趣味和应用极为广泛的一门学科。
图论的概念由瑞士数学家欧拉最早提出,欧拉在1736年发表的论文《依据几何位置的解题方法》中应用图的方法讨论了各尼斯堡七桥难题,见图3.1a和b所示。
图3.1 a 哥尼斯堡七桥 b 对应的图19~20世纪,图论主要研究一些游戏问题和古老的难题,如哈密顿图及四色问题。
1847年,基尔霍夫首先用图论来分析电网络,如今在电工领域,图论被用于网络分析和综合、通讯网络与开关网络的设计、集成电路布局及故障诊断、计算机结构设计及编译技术等等。
2. 电路的图电路的图是用以表示电路几何结构的图形,图中的支路和结点与电路的支路和结点一一对应,如图3.2所示,所以电路的图是点线的集合。
第三章电阻电路的一般分析◆重点:1、支路法2、节点法3、网孔法和回路法◆难点:1、熟练掌握支路法、网孔法和割集分析法的计算思路,会用这几种方法列写电路方程。
2、熟练地运用节点法和回路法分析计算电路。
3-1 电网络中的基本概念网络图论与矩阵论、计算方法等构成电路的计算机辅助分析的基础。
其中网络图论主要讨论电路分析中的拓扑规律性,从而便于电路方程的列写。
1.支路——Branch流过同一个电流的电路部分为一条支路。
2.节点——node三条或者三条以上支路的汇集称为节点。
4.网络的图——graph节点和支路的集合,称为图,每一条支路的两端都连接到相应的节点上。
6.回路——loop电路中的任意闭合路径,称为回路。
8.网孔——mesh一般是指内网孔。
平面图中自然的“孔”,它所限定的区域不再有支路。
例如:在下图中,支路数6,节点数4,网孔数3,回路数79.树一个连通图G的树T是指G的一个连通子图,它包含G的全部节点,但不含任何回路。
树中的支路称为“树支”——tree branch,图G中不属于T 的其他支路称为“连支”——link,其集合称为“树余”。
一个连通图的树可能存在多种选择方法。
10.基本回路只含一条连支的回路称为单连支回路,它们的总和为一组独立回路,称为“基本回路”。
树一经选定,基本回路唯一地确定下来。
对于平面电路而言,其全部网孔是一组独立回路。
3-2 2B 法与1B 法3.2.1 支路法(2B 法)介绍1.方法概述以支路电压和支路电流作为变量,对节点列写电流(KCL )方程,对回路列写电压(KVL )方程,再对各个支路写出其电压电流关系方程,简称支路方程。
从而得到含2b 个变量的2b 个独立方程。
又称为“2b 法”。
2.思路由上述方法可见,“2b 法”实际上清晰地体现了求解电路的两个不可或缺的方面,即电路的解一是要满足网络的拓扑约束,二是要满足电路中各个元件的伏安关系约束。
3.方程结构b 个支路方程,)1(-n 个电流(KCL )方程,))1((--n b 个电压(KVL )方程。
共2b 个独立方程,变量是b 个支路电流和b 个支路电压,共2b 个变量。
3.2.2 支路电流法简介(实际上,支路电压法可以类似地推出) 1.方法概述以支路电流作为变量,对独立节点列写电流(KCL )方程,对独立回路列写电压(KVL )方程,再由各个支路的支路方程将支路电压用支路电流表示出来。
从而得到含b 个变量的b 个独立方程。
又称为“1b 法”。
2.方程结构)1(-n 个电流(KCL )方程,))1((--n b 个电压(KVL )方程。
共b 个独立方程,变量是b 个支路电流。
3.2.3 解题步骤1.选定各个支路电流的参考方向;2.按KCL 对)1(-n 个独立节点列写电流方程;3.选取))1((--n b 个独立回路,指定回路的绕行方向,应用KVL ,列写电压方程;4.联立上述方程式,求解。
3.2.4 说明1.当电路存在纯电流源支路时,可以设电流源的端电压为变量,同时补充相应的方程。
2.实际解题时,适用于支路数少的电路出计算分析中。
3.2.5 例题已知:电路如图所示S2I求:用2b法及1b法的支路电流法及支路电压法列写求解电路各个支路电流的全部独立方程。
解:一、2b法⎪⎩⎪⎨⎧=-+=--=--53423114IIIIIIIIIS⎪⎩⎪⎨⎧=-+++=-+=--+22513211314UUUUUUUUUUUUSSS⎪⎪⎪⎩⎪⎪⎪⎨⎧=====555444333222111URIURIURIURIURI二、支路电流法⎪⎩⎪⎨⎧=-+=--=--53423114IIIIIIIIIS⎪⎩⎪⎨⎧=----=-+=--+2225511122111133144RIURIURIURIRIRIRIURISSS三、支路电压法⎪⎩⎪⎨⎧=-+++=-+=--+22513211314UUUUUUUUUUUUSSS⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=-+=--=--0005533442233111144R U R U R U R U R U R U R U R U I S3-3 网孔法与回路法网孔法实际上是回路法中的特殊情况。
所谓回路分析法是用数目少于支路电流数的“回路电流”代替支路电流作为电路方程中的变量,而通过回路电流可以推算出全部的支路电流的方法。
对于平面电路,可以按网孔取独立回路(至于原因,有关的图论中有详尽的证明)。
而对于非平面电路或者某些连接方式具有一定特点的平面电路,则采用回路分析法,即不一定选取网孔电流为独立变量。
3.3.1 网孔法一、方法概述选择电路的网孔电流作为独立变量,对各个网孔列写电压(KVL )方程,由于平面电路的全部网孔为一组独立回路,因此可以得到一组完备的独立电流方程,从而求解电路中的待求量。
我们仍然以支路法中提到的例题为例。
S2I实际上,设定了网孔电流、选择了网孔绕行方向后,就可以根据网孔的KVL 方程计算出各网孔电流,从而据此推出其他所有待求量,比如322I I I R -=,各节点电压可以直接根据列写各独立节点的KCL 方程来求取。
可见这里的所谓“网孔电流”,正是一组可以求解电路方程的完备的独立电量。
列写KVL 方程:网孔1:0)()(121331141=-+-++R I I R I I U R I S网孔2:0)()(212112=--+-U R I I R I I网孔3:0)()(2111322353=+--+-+S S U U R I I R I I R I写成矩阵形式:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++---+---++21132153223221131431S S S U U U U I I I R R R R R R R R R R R R R R补充方程: S I I -=2,即可解出待求量。
仔细观察可以看出,应用网孔法列写出来的方程组也十分有规律。
方程左边的系数矩阵的对角线上的元称为“自阻”,为网孔中各个电阻的和;系数矩阵的其他位置上的元称为“互阻”,符号为负,大小为两网孔间公共的电阻的和。
方程右边的列向量的各元为沿网孔绕行方向产生的电位升的电压源值的大小。
由于使用网孔法列写方程极具规律性,因此在实际使用网孔法解题时,只需根据电路的拓扑结构直接列写就可以了。
当然,其中的实际电流源要变换为实际电压源,以便计算。
二、说明1. 当电路存在纯电流源支路时,可以设电流源的端电压为变量,同时补充相应的方程。
2. 当电路中存在受控源时,可以将受控源按独立源一样处理,其后将受控源的控制量用网孔电流表示出来,然后移项。
3. 适用于支路多、网孔少的电路分析计算。
4. 只能运用于平面电路。
三、网孔法的矩阵形式m m m U I R =•其中:◆ R m ——网孔电阻矩阵。
其对角线上的元称为“自阻”,其值为某一网孔中联接的支路上的电阻之和,符号为正;其他各元称为“互阻”, 其值为某两个网孔共有支路上的电阻之和,符号为负。
◆ I m ——网孔电流向量。
其元为各个网孔的电流,为列向量。
◆ U m ——节点电压源向量。
其元为沿网孔参考方向产生的电压源电位升的和,为列向量。
例题:见P75:3-123.3.2 回路法一、方法以连支电流为变量,对用连支确定的基本回路列写KVL 方程,从而分析计算电路的方法。
在选择树时,应尽量将电流源或受控流源所在的支路选为连支,这样可以不再对由纯流源连支所确定的基本回路列写方程,从而进一步减少方程的数量。
解题方法与解题步骤基本与网孔法相同,所有可以运用网孔法求的电路均可使用回路法。
不同之处在于回路法应用面更广(它可以应用于非平面电路),而且在某些电路结构下可以简化计算。
二、回路法的矩阵形式l l l U I R =•其中:◆ R l ——回路电阻矩阵。
其对角线上的元称为“自阻”,其值为某一基本回路中联接的支路上的电阻之和,符号为正;其他各元称为“互阻”, 其值为某两个基本回路共有支路上的电阻之和,符号为负。
◆ I l ——连支电流向量。
其元为各个连支的电流,为列向量。
◆ U l ——回路电压源向量。
其元为沿基本回路参考方向产生的电压源电位升的和,为列向量。
三、例题1.已知:电路如图所示,我们可以注意到,这个电路虽然也是平面电路,各网孔也是独立回路,但是如果用网孔法解时会出现困难(请思考并查阅相应资料)。
此时,有两种方法可以解决:一是选择回路电流时将纯电流源支路选为回路独占的支路(即不把它作为两个回路的公共支路),然后以该电流源电流作为回路电流;另一个是将原电路中的电流源与跟它并联的电阻交换位置,使得电流源自然称为网孔独占的支路,并取电流源电流为网孔电流。
通过以上方法均可使得未知电流变量变为两个。
I 1 I 2 2.25k Ω- Ω 3k方法一I 2I 4电路对应的图及一组基本回路I I 2.25k Ω- 3k方法二求:各支路电流 解:方法一如图所示选择回路及回路电流,在此情况下,回路1、回路2的回路电流即为支路电流11和12,回路3的回路电流等于电流源的电流2mA ,因此只需建立两个回路方程就可以了。
自阻、互阻及每一回路中的电压源电位升的代数和为Ω=++=Ω=+=k R k R 25.5225.214132211Ω-==Ω-==k R R k R R 2132232112 0122211==S S U V U因此,回路1、2的回路方程为:01021025.5101121011043323131313=⨯-⨯+⨯-=⨯-⨯I I I I I 而:33102⨯=I ,可以解出:mA I 35.31=,mA I 4.12=。
所以 mA I 35.31=, mA I 4.12=, mA I 23=, mA I I I 6.0324-=-=,mA I I I 95.1215=-=方法二如图所示,将电流源与跟它并联的电阻调换位置,然后选择网孔电流为回路电流,在此情况下,网孔1、2、3的网孔电流即为支路电流11、12和电流源的电流13=2mA ,因此也只需建立两个回路方程就可以了。
自阻、互阻及每一回路中的电压源电位升的代数和为Ω=++=Ω=+=k R k R 25.5225.214132211Ω-==Ω-==k R R k R R 2132232112 0122211==S S U V U可见这与方法一中的完全相同。
因此,可以列写相同的回路方程。
后面的过程略去。
2.已知:电路如图ΩΩ5I 1求:各个支路电流解:分析:该电路既含有独立电流源,又含有受控电流源。
为了便于建立回路方程,且方便计算,可以将这二者分别划归回路1和回路3,从而使得这两个回路电流分别等于已知的独立电流源电流(15A )和受控源电流(9/X U ),于是就只需对回路2建立回路方程即可,再利用受控源与所涉及的回路电流之间的关系,就可以求解出待求量。