由弯矩图画剪力图
- 格式:doc
- 大小:60.50 KB
- 文档页数:2



轴,。
以表(a)(c)(1)(2) (3)≤ (4) 以剪力图是平行于轴的直线。
段的剪力为正,故剪力图在轴上方;段剪力为负,故剪力图在轴之下,如图8-12(b )所示。
由式(2)与式(4)可知,弯矩都是的一次方程,所以弯矩图是两段斜直线。
根据式(2)、(4)确定三点,, ,由这三点分别作出段与段的弯矩图,如图8-12(c )。
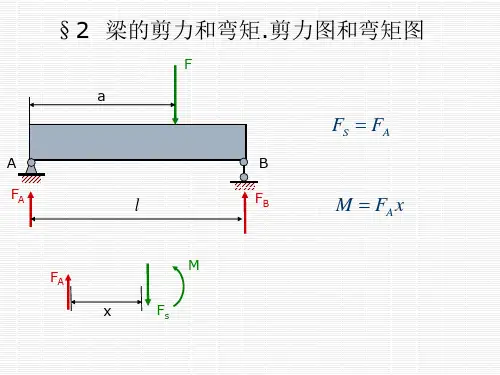
例8-4 简支梁受集度为的均布载荷作用,如图8-13(a )所示,作此梁的剪力图和弯矩图。
图8-13解 (1)求支反力 由载荷与支反力的对称性可知两个支反力相.即(2)列出剪力方程和弯矩方程 以梁左端为坐标原点,选取坐标系如图所示。
距原点为的任意横截面上的剪力和弯矩分别为x C l x AC x BC x x 0=x 0)(=x M a x =l Fabx M =)(l x =0)(=x M AC BC AB q A x解 (1)求支反力 由静力平衡方程,得(2)列剪力方程和弯矩方程 由于集中力作用在处,全梁内力不能用一个方程来表示,故以为界,分两段列出内力方程段0<≤ (1)0≤< (2)段 ≤< (3)≤≤(4) (3) 画剪力图和弯矩图 由式(1)、(3)画出剪力图,见图8-14(b );由式(2)(4)画出弯矩图,见图8-14(c )。
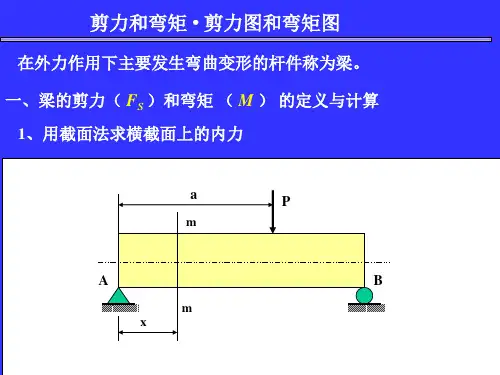
二、弯矩、剪力与分布载荷集度之间的微分关系在例8-4中,若将的表达式对取导数,就得到剪力。
若再将的∑=0)(x M A ∑=0)(x M B m C C AC l mF x F A Q ==)(x a xl m x F x M A ==)(x a BC l mF x F A Q ==)(a x l mx l mm x F x M A -=-=)(a x l )(x M x )(x F Q )(x F Q表达式对取导数,则得到载荷集度。
这里所得到的结果,并不是偶然的。
实际上,在载荷集度、剪力和弯矩之间存在着普遍的微分关系。
现从一般情况出发加以论证。




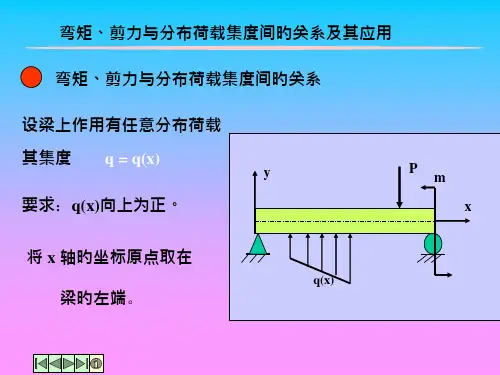
1.1.4 根据弯矩图作剪力图
1.1.4 根据弯矩图作剪力图
利用微分关系,可方便地根据弯矩图作剪力图。
(一)当M图为直线变化时
以图1-4a所示跨中作用集中荷载的简支梁为例,加以说明。
其M图和图分别示于图1-4b和图1-4c。
图1-4
在图1-4b中,循惯例,选取直角坐标系。
当我们分区段考察M图形与图形的关系时,若沿轴的指向,由左向右看,则将会看到如下客观规律:
第一,关于的符号:AC段,M“下坡”(M为增函数),则其相应的为正(M的一阶导数>0);CB段,M“上坡”(M为减函数),则其相应的为负(M的一阶导数<0)。
第二,关于的大小:可由M图形的“坡度”(斜率)确定,即,其中,为该区段长度,为图中该区段两端点弯矩值的高差。
而且,区段内图形“坡度”愈徒,剪力值愈大;“坡度”愈缓,剪力值愈小;“坡度”
为零(M图为水平直线),则剪力值亦为零(无剪力)。
二相邻区段的M图形“坡度”相同(当有集有力偶作用时),则其剪力值亦相同。
例如,本例中,AC段的剪力为
而CB段的剪力为
这一规律同样适用于竖杆或斜杆,只是须注意应沿杆轴“由左向右看”这一前提条件。
(二)当M图为二次抛物线变化时
根据M与的微分关系可判定,该图为斜直线。
因此,只须按照“一求两端
剪力,二引直线相连”的步骤,即可绘出该区段的图。
图1-5是根据已知弯矩图(图1-5a)绘出相应剪力轮廊图(图1-5b)的一个例子。
图1-5。