剪力图和弯矩图(基础)
- 格式:docx
- 大小:228.03 KB
- 文档页数:7








轴,。
以表(a)(b)(c)(1)(2) (3) ≤ (4)以剪力图是平行于轴的直线。
段的剪力为正,故剪力图在轴上方;段剪力为负,故剪力图在轴之下,如图8-12(b )所示。
由式(2)与式(4)可知,弯矩都是的一次方程,所以弯矩图是两段斜直线。
根据式(2)、(4)确定三点,,,由这三点分别作出段与段的弯矩图,如图8-12(c )。
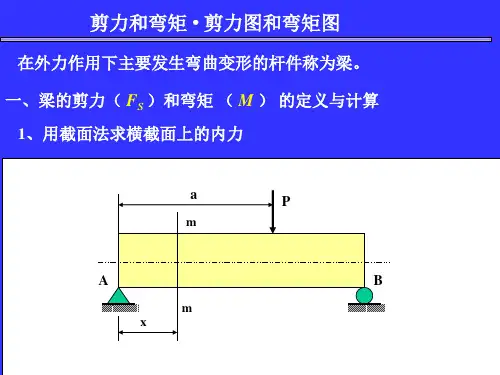
例8-4 简支梁受集度为的均布载荷作用,如图8-13(a )所示,作此梁的剪力图和弯矩图。
x C l x AC x BC x x 0=x 0)(=x M a x =l Fab x M =)(l x =0)(=x M AC BC AB q图8-13解 (1)求支反力 由载荷及支反力的对称性可知两个支反力相等,即(2)列出剪力方程和弯矩方程 以梁左端为坐标原点,选取坐标系如图所示。
距原点为的任意横截面上的剪力和弯矩分别为<< (1) 0≤≤ (2)(3)作剪力图和弯矩图 由式(1)可知,剪力图是一条斜直线,确定其上两点后即可绘出此梁的剪力图(图8-13b )。
由式(2)可知,弯矩图为二次抛物线,要多确定曲线上的几点,才能画出这条曲线。
例如通过这几点作梁的弯矩图,如图8-13(c )所示。
由剪力图和弯矩图可以看出,在两个支座内侧的横截面上剪力为最大值:。
在梁跨度中点横截面上弯矩最大,而在此截面上剪力。
例8-5 图8-14所示简支梁,跨度为,在截面受一集中力偶作用。
试列出梁的剪力方程和弯矩方程,并绘出梁的剪力图和弯矩图。
2ql F F B A ==A x qx ql qx F x F A Q -=-=2)(0x l 22122)(qx x ql x qx x F x M A -=-=x l 2maxql F Q=2max 81ql M =0=Q F l C m )(x F Q )(x M AB图8-14解 (1)求支反力 由静力平衡方程,得(2)列剪力方程和弯矩方程 由于集中力作用在处,全梁内力不能用一个方程来表示,故以为界,分两段列出内力方程段0<≤ (1)0≤< (2) 段≤< (3) ≤≤ (4)(3) 画剪力图和弯矩图 由式(1)、(3)画出剪力图,见图8-14(b );由式(2)(4)画出弯矩图,见图8-14(c )。

剪力弯矩图知识点总结1. 剪力和弯矩的概念剪力(shear force)指的是横截面上受力元的切向力,通常用V表示。
在悬臂梁上,剪力是垂直于截面的力,它的大小等于剪力截面上受力元的合力。
在弯曲情况下,不同截面上剪力的大小会有所不同。
弯矩(bending moment)指的是横截面上受力元的弯矩,通常用M表示。
弯矩是由悬臂梁上的外部力矩引起的,它的大小等于横截面上受力元的合力与该截面的距离之积。
在弯曲情况下,不同截面上弯矩的大小也会有所不同。
2. 剪力弯矩图的绘制原理绘制剪力弯矩图的基本原理是根据受力学原理和材料力学知识,将结构受力的情况在横截面上转化为剪力和弯矩的分布情况。
在绘制剪力弯矩图时,需要按照悬臂梁上的外部力作用位置和方向的不同,对每一个截面进行受力分析,然后根据受力平衡和截面内力的平衡方程来求解该截面上的剪力和弯矩。
通过不断地沿着结构轴线对不同截面进行受力分析,最终可以得到整个结构上的剪力和弯矩分布情况。
3. 剪力弯矩图的作用剪力弯矩图可以用于描述结构在不同位置上的受力情况,从而可以帮助工程师了解结构受力的性质和数量。
对于结构工程的设计和分析来说,剪力弯矩图可以为工程师提供重要的信息,例如结构的安全性、变形情况等。
此外,剪力弯矩图还可以用于指导设计和施工,帮助工程师做出合理的结构设计和构件选型。
4. 剪力弯矩图的绘制方法在绘制剪力弯矩图时,一般采用以下步骤:(1)确定结构的受力情况:首先需要了解结构上的外部力和力矩的作用位置和大小。
(2)取截面:根据要求,选择不同位置和数量的截面,并根据悬臂梁的几何形状和受力情况进行分析。
(3)受力分析:对每一个截面进行力学分析,求解该截面上的剪力和弯矩。
(4)绘制图表:根据受力分析结果,可以绘制剪力和弯矩图。
其中,剪力图通常用V-x 图表示,弯矩图通常用M-x图表示。
其中,V和M分别表示剪力和弯矩的大小,x表示截面的位置。
5. 剪力弯矩图的典型特点在剪力弯矩图中,具有以下一些典型特点:(1)剪力图的典型特点:通常在受力点附近出现剪力峰值,峰值的大小等于受力点的大小。

轴,。
以表(a)(c)(1)(2) (3)≤ (4) 以剪力图是平行于轴的直线。
段的剪力为正,故剪力图在轴上方;段剪力为负,故剪力图在轴之下,如图8-12(b )所示。
由式(2)与式(4)可知,弯矩都是的一次方程,所以弯矩图是两段斜直线。
根据式(2)、(4)确定三点,, ,由这三点分别作出段与段的弯矩图,如图8-12(c )。
例8-4 简支梁受集度为的均布载荷作用,如图8-13(a )所示,作此梁的剪力图和弯矩图。
图8-13解 (1)求支反力 由载荷与支反力的对称性可知两个支反力相.即(2)列出剪力方程和弯矩方程 以梁左端为坐标原点,选取坐标系如图所示。
距原点为的任意横截面上的剪力和弯矩分别为x C l x AC x BC x x 0=x 0)(=x M a x =l Fabx M =)(l x =0)(=x M AC BC AB q A x解 (1)求支反力 由静力平衡方程,得(2)列剪力方程和弯矩方程 由于集中力作用在处,全梁内力不能用一个方程来表示,故以为界,分两段列出内力方程段0<≤ (1)0≤< (2)段 ≤< (3)≤≤(4) (3) 画剪力图和弯矩图 由式(1)、(3)画出剪力图,见图8-14(b );由式(2)(4)画出弯矩图,见图8-14(c )。
二、弯矩、剪力与分布载荷集度之间的微分关系在例8-4中,若将的表达式对取导数,就得到剪力。
若再将的∑=0)(x M A ∑=0)(x M B m C C AC l mF x F A Q ==)(x a xl m x F x M A ==)(x a BC l mF x F A Q ==)(a x l mx l mm x F x M A -=-=)(a x l )(x M x )(x F Q )(x F Q表达式对取导数,则得到载荷集度。
这里所得到的结果,并不是偶然的。
实际上,在载荷集度、剪力和弯矩之间存在着普遍的微分关系。
现从一般情况出发加以论证。
图8-15设图8-15(a )所示简支梁,受载荷作用,其中有载荷集度为的分布载荷。
是的连续函数,规定向上为正,选取坐标系如图所示。
若用坐标为和的两个相邻横截面,从梁中取出长为的一段来研究,由于是微量,微段上的载荷集度可视为均布载荷,见图8-15(b ) 。
设坐标为的横截面上的内力为和,在坐标为的横截面上的内力为和。
假设这些内力均为正值,且在微段内没有集中力和集中力偶。
微段梁在上述各力作用下处于平衡。
根据平衡条件,得由此导出 (8-1) 设坐标为截面与梁轴线交点为C ,由,得略去二阶微量,可得(8-2)将式(8-2)对求一阶导数,并利用式(8-1),得(8-3)公式(8-1)~(8-3)就是载荷集度、剪力和弯矩之间的微分关系。
它表示:(1)横截面的剪力对的一阶导数,等于梁在该截面的载荷集度,即剪力图上某点切线的斜率等于该点相应横截面上的载荷集度。
(2)横截面的弯矩对的一阶导数,等于该截面上的剪力,即弯矩图上某点切线的斜率等于该点相应横截面上的剪力。
(3)横截面的弯矩对的二阶导数,等于梁在该截面的载荷集度。
由此表明弯矩图的变化形式与载荷集度的正负值有关。
若方向向下(负值),即<0,弯矩图为向上凸曲线;反之,方向向上(正值),则弯矩图为向下凸曲线。
根据微分关系,还可以看出剪力和弯矩有以下规律:(1) 梁的某一段内无载荷作用,即,由可知,常量。
若,剪力图为沿轴的直线,并由可知,常量,弯矩图为平行于轴的直线。
若等于常数,剪力图为平行于轴的直线,弯矩图为向上或向下倾斜的直线。
(2)梁的某一段内有均布载荷作用,即等于常数,则剪力是的一次函数,弯矩是的二次函数。
剪力图为斜直线;若为正值,斜线向上倾斜;若负值,斜线向下倾斜。
弯矩图为二次抛物线,当为正值,即>0时,弯矩x q )(x q )(x q x x x x d +x d x d )(x q x )(x F Q )(x M x x d +)(d )(x F x F Q Q +)(d )(x M x M +x d ∑=0y F )(d )(d x q x x F Q =x x d +∑=0C M 2d d )(xxx q )(d )(d x F x x M Q =x )(d )(d 22x q x x M =)(x q )(x F Q )(x M x x x )(x q )(x q )(x q )(d )(d 22x q x x M =)(x q 0)(=x q 0)(d )(d ==x q x x F Q =)(x F Q 0)(=x F Q x 0)(d )(d ==x F x x M Q =)(x M x )(x F Q x )(x q )(x F Q x )(x M x )(x q )(x q )(x q )(d )(d 22x q x x M =例8-6 图8-16(a )所示简支梁,受均布(a) 载荷和集中力共同作用,试绘梁的内力图。
解 (1)计算支反力 由,得(b) 所以由,得 (c)得(2)根据载荷作用位置把梁分成三段,并 图8-16对各段的内力图形状作出分析判断,求出各段内力图的起点、终点和极值点的内力值,然后∑=0)(F A M 0kN 62)(=⨯-⨯+⨯⨯-AD F AC ABAB q D kN3kN 6212=⨯+⋅-=AD AC AB q F D ∑=0y F kN 3=A F(3)根据上表,由左至右逐段画出剪力图,如图8-16(b ) 所示;画出弯矩图,如图8-17(c )所示,可见,。
例8-7 外伸梁与其所受载荷如图8-17(a )所示,试作梁的剪力图和弯矩图。
图8-17解 按照前述使用的方法作剪力图和弯矩图时,应分段列出剪力方程与弯矩方程,然后按方程作图。
现利用本节所得结论,可以不列方程而直接作图。
(1)求支反力 由和可求得,(2)分段 沿集中力作用线、均布载荷的始末端以与集中力偶所在位置进行分段。
现将梁分为.、四段。
(3) 作剪力图段 在支反力的右侧梁截面上,剪力为。
截面到截面之间的载荷为均布载荷,即常数。
剪力图为斜直线。
算出集中力左侧梁截面上剪力 即可确定这条斜直线,见图8-17(b )。
段 截面处有一集中力,剪力图发生突变,变化的数值等于。
故从到剪力图又为斜直线,知段 截面与截面之间梁上无载荷,剪力图为水平线。
段 截面与截面之间剪力图也为水平线,算出截面右侧截面上的,即可画出这一水平线。
(4) 作弯矩图段 截面上弯矩为零。
从到梁上为均布载荷,且均布载荷向下,则弯矩图为上凸的抛物线。
算出截面的弯矩为已知点、点弯矩以与抛物线为上凸,即可大致画出段的弯矩图。
段 由受力特性可知,从到弯矩图为上凸的另一抛物线。
截面的剪力突变,故弯矩图在点斜率也突变。
在截面上的剪力等于零,故点为弯矩的极值点。
由段的剪力方程可计算出至梁左端距离为,故可求出截面上弯矩的极值为 在集中力偶左侧截面上弯矩为已知、与等三个截面上的弯矩,即可连成到之间的抛物线。
段和段 截面上有一集中力偶,弯矩图突变,而且变化的数值等于。
所以在右侧截面上为截面上的弯矩为由于段的剪力图为水平直线,于是由和就确定了这条直线。
到之间弯矩图也是斜直线,由于,故可画出图示斜直线。
从所得的剪力图(图8-17b )和弯矩图(图8-17c )上,不难确定最大剪力,最大弯矩。
kN 3max =Q F m kN 3max ⋅=M ∑=0)(F A M ∑=0)(F B M kN 7=A F kN 5=B F AE AC CD DB BE AC A F kN 7A C =AC q 1F 左QC FCD C 1F 1F C D DB D B BE B E B =右QB F kN 2AC A A C C A C AC CD C D C C F F CD F 5m F 0M 左D M m 16kN m kN 881214287211⋅=⋅⨯⨯⨯-⨯-⨯=⨯⨯-⨯-⨯=)(左AD AD q CD F AD F M A D C F 左DC D DB BE D m kN 100⋅=M D 右D M B B M DB 右D MB M B E 0=E M kN7max=QF mkN 5.20max ⋅=M要注意的是:不但可能发生在的截面上,也有可能发生在集中力或集中力偶作用处。
所以求弯矩的最大值时,应综合考虑上述几种可能性。
先假设M 求为某一方向,(一般我是假设为逆时针,书上好像是把逆时针方向规定为正方向),然后对该分离体(或研究对象)列弯矩平衡方程(当然必须是在分离体弯矩平衡情况下):M 总=0。
即MA+MB+MC+M 求=0。
(注意对于MA 、MB 、MC ,如果是逆时针的取正值,顺时针取负值。
),此时如果球出的M 求为正值,则它就是逆时针的,如果是负值,那它的方向与假设方向是相反的,是顺时针。
也可以把所有顺时针的弯矩全取正值放在等号左边相加,把所有逆时针的也取正值但放在等号右边相加(其实跟上面是一样的,也是得假设M 求为某一方向)列平衡方程。
那还不简单,不同X 对应不同的弯矩了,要看X 等于多少了。
不知道你的是不是结构构件上的弯矩,结构力学上梁的弯矩正负判断原则是使梁的上表面受拉的弯矩为正,反之为负。
我不知道你的原题是什么样的,X 表示的是什么。
如果X 表示的是位置坐标,那么M 求=AX²+BX+C 表示的是构件上的弯矩分布函数,不同位置对应不同的弯矩,也就是说构件上弯矩有的地方正有的地方负,凡是求出是正值的就与假设方向或默认方向相同,反之相反。
如果X 表示的是某个构件的长度,也是一样判方法。
还有一个可能是你所算的是一种动态情况,就是某个东西在动,导致弯矩是个变量,也是一样的。
总之一句话,要看X 值的情况。
最好把原题放上来,这样更有针对性。
你的应该是结构力学方面的,结构力学上梁的弯矩正负判断原则是使梁的上表面受拉的弯矩为正,反之为负。
所以假设时应假设成如图方向。
弯矩图都是画在受拉一侧的,所以凡是出现正值的区域就把弯矩图画在上面,出现负值的就画在下面,过度地带就是为0的地方。
强调一下,假设没有什么对或错的,M 求>0对应的X 处弯矩跟假设的方向就是相同的,正的,M 求<0对应的XX 围处弯矩方向就是跟假设相反,无论假设方向怎么样求出的弯矩都是一样的。
、一般规定 梁的哪侧纤维受拉就画在哪侧的 一般规定下侧受拉为正弯矩。
建筑力学中弯矩剪力图方向悬赏分:30 - 解决时间:2010-2-2 11:27我不知道画上边还是下边左边还是右边,希望举个简支梁的例子详细说明说的明了给加分 你把梁想象成柔性的,梁的变形和图像要一致!即往哪儿变形画那边比如,简支梁上面作用一集中力,画下面。
如果作用一力偶,1,力偶顺时针时,左边上,右边下;2力偶逆时针时,相反。