2019-2020学年江西师大附中高一(上)10月月考数学试卷

江西师大附中2019-2020高一年级10月月考数学试题命题人：郑辉平 审题人：朱涤非第Ⅰ卷（共60分）一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．函数()()0112x f x x x -=+--的定义域为（ ） A ．[)1,+∞ B ．()1,+∞C ．()()1,22,+∞D ．[)()1,22,+∞【答案】C2．图中阴影部分所表示的集合是（ ）A.()U B A CB. ()()C B B AC.()()U A C BD. ()()U A C B【答案】C3．给出下列关系式：2Q ； ②{1,2}{(1,2)}=； ③2{1,2}∈； ④{0}∅⊆，其中正确关系式的个数是（ ）A ．0B ．1C ．2D ．3【答案】C4．下列集合中子集个数最多的是（ ）A ．{}2|320x N x x ∈++=B ．{|x x 是边长分别为123，，的三角形}C ．{|||1}x R x ∈=-D ．{}∅【答案】D5.下列各组中的两个函数是同一函数的为（ ）A ．(3)(5)(),()53x x f x g x x x +-==-+ B ．2(),()f x x g x x == C ．()25,()25f x x g x x =-=-D ．33(),()f x x g t t ==【答案】D6.已知函数2()25f x x ax =-+，且其对称轴为1x =，则以下关系正确的是( )A. (3)(2)(8)f f f -<<B. (2)(3)(8)f f f <-<C. (3)(2)(8)f f f -=<D. (2)(8)(3)f f f <<-【答案】B 【解析】根据题意，函数52)(2+-=ax x x f ，其对称轴为1=x ，其开口向上，)(x f 在),1[+∞上单调递增，则有)8()5()3()2(f f f f <=-<，故选B.7.若()()()()⎩⎨⎧≥-<-=10,610,2x x f x x x f ,则(57)f 的值为（ ） A. 1 B.3 C.5 D. 7【答案】D【解析】由题意得，729)9()45()51()57(=-==⋅⋅⋅===f f f f8.设}5,4,3,2,1{=U ，B A ,为U 的子集，若}2{=B A ，((){4}U A B =,()(){1,5}U U A B =，则下列结论正确的是（ ） A ．3,3A B ∉∉ B ．3,3A B ∉∈ C ．3,3A B ∈∉ D ．3,3A B ∈∈ 【答案】C 9.若函数223,1()1,1x ax x f x ax x ⎧++≤=⎨+>⎩是减函数，则a 的取值范围是（ ）A.[3,1]--B.(,1]-∞-C.[1,0)-D.[2,0)- 【答案】A10．定义集合的商集运算为},,|{B n A m nm x x B A ∈∈==，已知集合}6,4,2{=A ， },12|{A k k x x B ∈-==，则集合B AB 元素的个数为( ) A ．7 B ．8C ．9D ．10 【答案】A 【解析】由题意知，}2,1,0{=B ，}31,1,61,41,21,0{=A B，则}2,31,1,61,41,21,0{=B A B ，共有7个元素，选A.11．已知()x x f 23-=，()x x x g 22-=，()()()()()()(),,g x f x g x F x f x f x g x ≥⎧⎪=⎨<⎪⎩若若，则()x F 的最值是（ ）A.最大值为3-，最小值为1-B.最大值为727-，无最小值C.最大值为3，无最小值D.既无最大值，又无最小值【答案】B 【解析】如图实线部分可知， 有最大值为727-，无最小值，故选B.12．已知函数1()()0()x f x x ⎧=⎨⎩为有理数为无理数，则关于函数有如下说法：①的图像关于y 轴对称； ②方程的解只有；③任取一个不为零的有理数T ，)()(x f T x f =+对任意的R x ∈恒成立； ④不存在三个点))(,(11x f x A ，))(,(22x f x B ,))(,(33x f x C ，使得ABC ∆为等边三 角形． ()f x ()f x (())f f x x =1x =。

3.2.2奇偶性基础过关练题组一函数奇偶性的概念及其图象特征1.已知一个奇函数的定义域为{-1,2,a,b},则a+b等于()A.-1B.1C.0D.22.若y=f(x)(x∈R)是奇函数,则下列坐标表示的点一定在y=f(x)图象上的是()A.(a,-f(a))B.(-a,-f(a))C.(-a,-f(-a))D.(a,f(-a))3.下列图象表示的函数中具有奇偶性的是()4.(2020北京通州高一上期末)能说明“若f(x)是奇函数,则f(x)的图象一定过原点”是假命题的一个函数是f(x)=.5.(1)如图①,给出奇函数y=f(x)的部分图象,试作出y轴右侧的图象并求出f(3)的值;(2)如图②,给出偶函数y=f(x)的部分图象,试作出y轴右侧的图象并比较f(1)与f(3)的大小.题组二函数奇偶性的判定6.已知y=f(x),x∈(-a,a),F(x)=f(x)+f(-x),则F(x)()A.是奇函数B.是偶函数C.既是奇函数又是偶函数D.是非奇非偶函数7.(2019四川雅安中学高一上第一次月考)下列函数中是偶函数,且在区间(0,1)上为增函数的是( ) A.y=|x| B .y=3-x C.y=1xD.y=-x 2+4 8.若函数f(x)={1,x >0,-1,x <0,则f(x)( )A.是偶函数B.是奇函数C.既是奇函数又是偶函数D.既不是奇函数又不是偶函数 9.判断下列函数的奇偶性: (1)f(x)=√x 2-1+√1-x 2;(2)f(x)=2x 2+2x x+1;(3)f(x)={x(1-x)(x <0),x(1+x)(x >0).题组三 函数奇偶性的综合运用10.已知函数f(x)=mx 2+nx+2m+n 是偶函数,其定义域为[m+1,-2n+2],则( )A.m=0,n=0B.m=-3,n=0C.m=1,n=0D.m=3,n=011.(2020广西柳州二中高一上月考)已知函数f(x)是定义在R 上的奇函数,当x ∈(-∞,0)时,f(x)=2x 3+x 2,则f(2)=( ) A.20 B.12 C.-20 D.-1212.(2020广东珠海高一上期末学业质量检测,)已知函数f(x)为R 上的奇函数,且在(-∞,0)上是增函数, f(5)=0,则xf(x)>0的解集是 .13.已知y=f(x)是奇函数,当x<0时,f(x)=x 2+ax,且f(3)=6,则a 的值为 .14.(2020广东湛江一中高一上期中)已知f(x),g(x)分别是定义在R 上的偶函数和奇函数,且f(x)-g(x)=x 3+x 2+1,则f(1)+g(1)= . 15.(2019天津南开高一上期末)已知f(x)是定义在R 上的偶函数,当x ≥0时, f(x)=x 2-2x.(1)求函数f(x)的解析式,并画出函数f(x)的图象;(2)根据图象写出f(x)的单调区间和值域.能力提升练题组一函数奇偶性的概念及其图象特征1.()已知y=f(x)是偶函数,其图象与x轴有4个交点,则方程f(x)=0的所有实数根之和是()A.4B.2C.1D.02.(多选)()若f(x)为R上的奇函数,则下列四个说法正确的是()A.f(x)+f(-x)=0B.f(x)-f(-x)=2f(x)C.f(x)·f(-x)<0D.f(x)=-1f(-x)3.()f(x)是定义在R上的奇函数,其在[0,+∞)上的图象如图所示.(1)画出f(x)的图象;(2)解不等式xf(x)>0.题组二函数奇偶性的判定4.(2020黑龙江哈三中高一上第一次阶段性验收,)下列函数是偶函数的是()A.f(x)=x3-1x B.f(x)=√1-x2|x-2|-2C.f(x)=(x-1)√1+x1-xD.f(x)=|2x+5|+|2x-5|5.()已知F(x)=(x3-2x)f(x),且f(x)是定义在R上的奇函数,f(x)不恒等于零,则F(x)为()A.奇函数B.偶函数C.奇函数或偶函数D.非奇非偶函数6.()已知f(x+y)=f(x)+f(y)对任意实数x,y都成立,则函数f(x)是()A.奇函数B.偶函数C.既是奇函数,也是偶函数D.既不是奇函数,也不是偶函数7.(多选)()设函数f(x),g(x)的定义域都为R,且f(x)是奇函数,g(x)是偶函数,则下列结论中正确的是()A.|f(x)|g(x)是奇函数B.f(x)|g(x)|是奇函数C.f(x)+|g(x)|是偶函数D.|f(x)|+g(x)是偶函数题组三函数奇偶性的综合运用8.(2020河北承德一中高一上月考,)若偶函数f(x)在(-∞,-1]上单调递增,则()A.f(-32)<f(-1)<f(2)B.f(-1)<f(-32)<f(2)C.f(2)<f(-1)<f(-32)D.f(2)<f(-32)<f(-1)9.(2020黑龙江大庆实验中学高一上月考,)函数f(x)在(-∞,+∞)上单调递减,且为奇函数.若f(1)=-1,则满足-1≤f(x-1)≤1的x的取值范围是()A.[-2,2]B.[-1,1]C.[0,2]D.[1,3]10.(2020河南郑州高一上期末,)已知定义在R上的奇函数f(x)满足f(x+4)=f(x)恒成立,且f(1)=1,则f(3)+f(4)+f(5)的值为(深度解析)A.-1B.1C.2D.011.(2020江西临川一中高一上月考,)已知函数f(x)与g(x)分别是定义域上的奇函数与偶函数,且f(x)+g(x)=x2-1x+1-2,则f(2)=()A.-23B.73C.-3D.11312.(2019四川成都高一上期末调研,)已知f(x)是定义在R 上的奇函数,且当x ≥0时, f(x)={-x,0≤x ≤1,-1,1<x <2,x -3,x ≥2.若对任意的x ∈R,不等式f(x)>f(x-√2a)恒成立,则实数a 的取值范围是 . 13.(2019天津河西高一上期末,)(1)若奇函数f(x)是定义在R 上的增函数,求不等式f(2x-1)+f(3)<0的解集;(2)若f(x)是定义在R 上的偶函数,且在区间[0,+∞)上是增函数,求不等式f(2x-1)-f(-3)<0的解集.14.(2020安徽师大附中高一上月考,)已知函数f(x)=ax+b1+x 2是定义在(-1,1)上的奇函数,且f (12)=25.(1)求函数f(x)的解析式;(2)用定义证明f(x)在(-1,1)上是增函数; (3)解关于实数t 的不等式f(t-1)+f(t)<0.15.(2020山东菏泽高一上期末联考,)已知函数f(x)=x 2+2a-3x是奇函数.(1)求函数f(x)的解析式;(2)若函数f(x)在(0,√p)上单调递增,试求p的最大值.16.()设函数f(x)=x2-2|x-a|+3,x∈R.(1)王鹏同学认为,无论a取何值,f(x)都不可能是奇函数.你同意他的观点吗?请说明你的理由;(2)若f(x)是偶函数,求a的值;(3)在(2)的情况下,画出y=f(x)的图象并指出其单调递增区间.深度解析答案全解全析基础过关练1.A因为该奇函数的定义域为{-1,2,a,b},且奇函数的定义域关于原点对称,所以a与b中一个等于1,一个等于-2,所以a+b=1+(-2)=-1,故选A.2.B∵f(x)为奇函数,∴f(-a)=-f(a),∴点(-a,-f(a))在函数y=f(x)的图象上.3.B选项A中的图象关于原点或y轴均不对称,故排除;选项C、D中的图象所示的函数的定义域不关于原点对称,不具有奇偶性,故排除;选项B中的图象关于y轴对称,其表示的函数是偶函数.故选B.(答案不唯一)4.答案1x,答案不唯一.解析举出x=0不在定义域内的奇函数即可,如f(x)=1x5.解析(1)由奇函数的性质可作出它在y轴右侧的图象,如图①所示,易知f(3)=-2.(2)由偶函数的性质可作出它在y轴右侧的图象,如图②所示,易知f(1)>f(3).6.B∵x∈(-a,a),其定义域关于原点对称,且F(-x)=f(-x)+f(x)=F(x),∴F(x)是偶函数.7.A选项A中,函数y=|x|为偶函数,且在区间(0,1)上为增函数,故A符合题意;选项B中,函数y=3-x为非奇非偶函数,且在区间(0,1)上为减函数,故B不符合题意;选项C中,函数y=1为奇函数,且在区间(0,1)上为减x函数,故C不符合题意;选项D中,函数y=-x2+4为偶函数,在区间(0,1)上为减函数,故D不符合题意.8.B作出函数f(x)的图象,如图所示,可以看出该图象关于原点对称,故f(x)为奇函数.9.解析(1)依题意得x2-1≥0,且1-x2≥0,即x=±1,因此函数f(x)的定义域为{-1,1},关于原点对称,且f(x)=0.∵f(-x)=-f(x),f(-x)=f(x),∴f(x)既是奇函数又是偶函数.(2)函数f(x)的定义域是(-∞,-1)∪(-1,+∞),不关于原点对称,∴f(x)是非奇非偶函数.(3)易得函数f(x)的定义域是D=(-∞,0)∪(0,+∞),关于原点对称.任取x∈D,当x>0时,-x<0,∴f(-x)=(-x)[1-(-x)]=-x(1+x)=-f(x);当x<0时,-x>0,∴f(-x)=-x(1-x)=-f(x),∴f(x)为奇函数.10.B由f(x)=mx2+nx+2m+n是偶函数,得n=0.又函数的定义域为[m+1,-2n+2],所以m+1=2n-2,则m=-3.11.B由题意得f(2)=-f(-2)=-[2×(-2)3+(-2)2]=12.12.答案(-∞,-5)∪(5,+∞)解析∵f(x)为R上的奇函数,∴f(0)=0.∵f(x)在(-∞,0)上是增函数,f(5)=0,∴f(x)在(0,+∞)上是增函数,f(-5)=0.可大致用图象表示:∵xf(x)>0等价于x与f(x)同号,且均不为0,∴结合图象知解集是(-∞,-5)∪(5,+∞).13.答案5解析因为f(x)是奇函数,所以f(-3)=-f(3)=-6,所以(-3)2+a×(-3)=-6,解得a=5.14.答案1解析由题意可得f(1)+g(1)=f(-1)-g(-1)=(-1)3+(-1)2+1=1.15.解析(1)∵x≥0时,f(x)=x2-2x,∴当x<0时,-x>0,∴f(-x)=x2+2x,∴f(-x)=f(x)=x 2+2x. 故函数f(x)的解析式为 f(x)={x 2-2x,x ≥0,x 2+2x,x <0,函数f(x)的图象如图所示.(2)由(1)中函数的图象可知,函数f(x)的单调递增区间为[-1,0],[1,+∞);单调递减区间为(-∞,-1],[0,1].函数f(x)的值域为[-1,+∞).能力提升练1.D 因为y=f(x)是偶函数,所以y=f(x)的图象关于y 轴对称,所以f(x)=0的所有实数根之和为0.2.AB ∵f(x)在R 上为奇函数,∴f(-x)=-f(x),∴f(x)+f(-x)=f(x)-f(x)=0,故A 正确; f(x)-f(-x)=f(x)+f(x)=2f(x),故B 正确;当x=0时,f(x)·f(-x)=0,故C 不正确;当x=0时,f(x)f(-x)的分母为0,无意义,故D 不正确.3.解析 (1)根据奇函数的图象关于原点对称,可得f(x)的图象如图所示.(2)xf(x)>0即图象上点的横坐标与纵坐标同号,且均不为0.结合图象可知,xf(x)>0的解集是(-2,0)∪(0,2).4.D 在选项A 中,f(x)=x 3-1x(x ≠0), f(-x)=-x 3+1x,f(-x)=-f(x),是奇函数;在选项B 中,f(x)=√1-x 2|x -2|-2=√1-x 2-x(-1≤x ≤1,x ≠0),f(-x)=√1-x 2x, f(-x)=-f(x),是奇函数;在选项C 中,f(x)=(x-1)·√1+x 1-x(-1≤x<1),是非奇非偶函数;在选项D中,f(x)=|2x+5|+|2x-5|(x ∈R), f(-x)=|-2x+5|+|-2x-5|=|2x+5|+|2x-5|, f(x)=f(-x),是偶函数,故选D.5.B 依题意得F(x)的定义域为R,且F(-x)=(-x 3+2x)f(-x)=(x 3-2x)f(x)=F(x),所以F(x)为偶函数,故选B. 6.A 令x=y=0,得f(0)=f(0)+f(0), 所以f(0)=0.又因为f(x-x)=f(x)+f(-x)=0,所以f(-x)=-f(x),所以f(x)是奇函数,故选A. 7.BD A 中,令h(x)=|f(x)|g(x),则h(-x)=|f(-x)|g(-x)=|-f(x)|g(x)=|f(x)|·g(x)=h(x),∴A 中函数是偶函数,A 错误;B 中,令h(x)=f(x)|g(x)|,则h(-x)=f(-x)·|g(-x)|=-f(x)|g(x)|=-h(x),∴B 中函数是奇函数,B 正确;C 中,由f(x)是奇函数,可得f(-x)=-f(x),由g(x)是偶函数,可得g(-x)=g(x),由f(-x)+|g(-x)|=-f(x)+|g(x)|知C 错误;D 中,由|f(-x)|+g(-x)=|-f(x)|+g(x)=|f(x)|+g(x),知D 正确.故选BD.8.D 由f(x)是偶函数且在(-∞,-1]上单调递增,得f(x)在[1,+∞)上单调递减, f (-32)=f (32),f(-1)=f(1),又因为2>32>1,所以f(2)<f (32)<f(1),即f(2)<f (-32)<f(-1),故选D. 9.C 因为f(x)为奇函数,且f(1)=-1,所以f(-1)=1, 所以-1≤f(x-1)≤1等价于f(1)≤f(x-1)≤f(-1).由函数f(x)在(-∞,+∞)上单调递减,可得-1≤x-1≤1,解得0≤x ≤2. 故选C.10.D ∵f(x)是R 上的奇函数, f(1)=1, ∴f(-1)=-f(1)=-1, f(0)=0.依题意得f(3)=f(-1+4)=-f(1)=-1,f(4)=f(0+4)=f(0)=0,f(5)=f(1+4)=f(1)=1. 因此, f(3)+f(4)+f(5)=-1+0+1=0,故选D.陷阱提示 在有关奇函数f(x)的求值问题中,要注意当f(x)在x=0处有意义时, f(0)=0这个特殊情况,否则可能会出现已知条件不足,导致问题解决不了的情况. 11.A ∵f(x)+g(x)=x 2-1x+1-2①,∴f(-x)+g(-x)=(-x)2-1-x+1-2=x 2-1-x+1-2,又∵函数f(x)与g(x)分别是定义域上的奇函数与偶函数, ∴f(-x)=-f(x),g(-x)=g(x), ∴f(-x)+g(-x)=-f(x)+g(x)=x 2-1-x+1-2②, 联立①②消去g(x),得f(x)=-12x+2+1-2x+2,∴f(2)=-12×2+2+1-2×2+2=-23.故选A.12.答案 (3√2,+∞)解析 由已知条件画出函数f(x)的图象(图中实线部分),若对任意的x ∈R,不等式 f(x)>f(x-√2a)恒成立,则函数f(x)的图象始终在函数f(x-√2a)的图象的上方.当a<0时,将函数f(x)的图象向左平移,不能满足题意,故a>0,将函数f(x)图象向右平移时的临界情况是当D 点与B 点重合,且临界情况不满足题意,由图可知,向右平移的√2a 个单位长度应大于6,即√2a>6,解得a>3√2,故答案为(3√2,+∞).13.解析 (1)由题知f(x)为奇函数,且在R 上是增函数,则f(2x-1)+f(3)<0⇒f(2x-1)<-f(3)⇒f(2x-1)<f(-3)⇒2x-1<-3,解得x<-1,即不等式的解集为(-∞,-1).(2)由题知f(x)是定义在R 上的偶函数,且在区间[0,+∞)上是增函数, 则f(2x-1)-f(-3)<0⇒f(2x-1)<f(3)⇒f(|2x-1|)<f(3)⇒|2x-1|<3,解得-1<x<2, 即不等式的解集为(-1,2). 14.解析 (1)因为函数f(x)=ax+b 1+x 2是定义在(-1,1)上的奇函数,所以f(0)=0,得b=0. 又知f (12)=25,所以12a 1+14=25,解得a=1,所以f(x)=x1+x 2.(2)证明:∀x 1,x 2∈(-1,1),且x 1<x 2,则f(x 2)-f(x 1)=x 21+x 22-x 11+x 12=(x 2-x 1)(1-x 1x 2)(1+x 12)(1+x 22),由于-1<x 1<x 2<1,所以-1<x 1x 2<1,即1-x 1x 2>0, 所以(x 2-x 1)(1-x 1x 2)(1+x 12)(1+x 22)>0,即f(x 2)-f(x 1)>0,所以f(x)在(-1,1)上是增函数.(3)因为f(x)是奇函数, 所以f(-x)=-f(x),所以f(t-1)+f(t)<0等价于f(t-1)<-f(t)=f(-t),即f(t-1)<f(-t), 又由(2)知f(x)在(-1,1)上是增函数,所以{-1<t -1<1,-1<-t <1,t -1<-t,解得0<t<12,即原不等式的解集为{t |0<t <12}.15.解析 (1)因为函数f(x)=x 2+2a -3x是奇函数,所以f(x)=-f(-x),即x 2+2a -3x=-x 2+2a+3x,化简得a=0, 所以f(x)=x 2+2-3x.(2)f(x)=x 2+2-3x =-13(x 2+2x)=-13·(x +2x ),任取x 1,x 2∈(0,+∞)且x 1≠x 2,则Δf(x)Δx=f(x 2)-f(x 1)x 2-x 1=-13(x 2+2x 2)-[-13(x 1+2x 1)]x 2-x 1=-13(x 2-x 1+2x 2-2x 1)x 2-x 1=-13·(x 2-x 1)(1-2x 1x 2)x 2-x 1=-13·x 1x 2-2x 1x 2.因为x 1,x 2∈(0,+∞),所以x 1x 2>0. 当x 1,x 2∈(0,√2]时,x 1x 2-2<0,从而Δf(x)Δx>0;当x 1,x 2∈[√2,+∞)时,x 1x 2-2>0,从而Δf(x)Δx<0.因此f(x)在(0,√2]上是增函数, f(x)在[√2,+∞)上是减函数.由题知f(x)在(0,√p]上单调递增,所以√p的最大值为√2,即p的最大值为2.16.解析(1)我同意王鹏同学的观点.理由如下:假设f(x)是奇函数,则由f(a)=a2+3,f(-a)=a2-4|a|+3,可得f(a)+f(-a)=0,即a2-2|a|+3=0,显然a2-2|a|+3=0无解,∴f(x)不可能是奇函数.(2)若f(x)为偶函数,则有f(a)=f(-a),即a2+3=a2-4|a|+3,解得a=0.经验证,此时f(x)=x2-2|x|+3是偶函数.(3)由(2)知f(x)=x2-2|x|+3,其图象如图所示,由图可得,其单调递增区间是(-1,0)和(1,+∞).解题模板利用奇偶性确定函数解析式中参数的值时,选择题、填空题中可用特殊值法简化运算;解答题中要结合定义写出完整的解题过程,若用特殊值法得到参数的值仍需要进一步证明.。

公司理财(罗斯光盘)篇一：罗斯《公司理财》(第9版)网授精讲班江西省南昌市2019-2019学年度第一学期期末试卷（江西师大附中使用）高三理科数学分析试卷紧扣教材和考试说明，从考生熟悉的基础知识入手，多角度、多层次地考查了学生的数学理性思维能力及对数学本质的理解能力，立足基础，先易后难，难易适中，强调应用，不偏不怪，达到了“考基础、考能力、考素质”的目标。

试卷所涉及的知识内容都在考试大纲的范围内，几乎覆盖了高中所学知识的全部重要内容，体现了“重点知识重点考查”的原则。

1．回归教材，注重基础试卷遵循了考查基础知识为主体的原则，尤其是考试说明中的大部分知识点均有涉及，其中应用题与抗战胜利70周年为背景，把爱国主义教育渗透到试题当中，使学生感受到了数学的育才价值，所有这些题目的设计都回归教材和中学教学实际，操作性强。

2．适当设置题目难度与区分度选择题第12题和填空题第16题以及解答题的第21题，都是综合性问题，难度较大，学生不仅要有较强的分析问题和解决问题的能力，以及扎实深厚的数学基本功，而且还要掌握必须的数学思想与方法，否则在有限的时间内，很难完成。

3．布局合理，考查全面，着重数学方法和数学思想的考察在选择题，填空题，解答题和三选一问题中，试卷均对高中数学中的重点内容进行了反复考查。

包括函数，三角函数，数列、立体几何、概率统计、解析几何、导数等几大版块问题。

这些问题都是以知识为载体，立意于能力，让数学思想方法和数学思维方式贯穿于整个试题的解答过程之中。

二、亮点试题分析1．【试卷原题】11已知,,是单位圆上互不相同的三点，且满足?，则?的最小值为（）????141．?23．?4．?1．?【考查方向】本题主要考查了平面向量的线性运算及向量的数量积等知识，是向量与三角的典型综合题。

解法较多，属于较难题，得分率较低。

???【易错点】1．不能正确用，，表示其它向量。

????2．找不出与的夹角和与的夹角的倍数关系。

2019-2020学年北京师大附中高一（上）第一次月考数学试卷一、选择题共8小题，每小题4分，共32分。

在每小题列出的四个选项中，选出符合题目要求的一项。

1．（4分）设集合A＝{0，1，2，3}，集合B＝{2，3，4}，则A∩B＝（）A．{2，3}B．{0，1}C．{0，1，4}D．{0，1，2，3，4} 2．（4分）命题“∃x0∈R，x02+x0+1＜0”的否定为（）A．不存在x0∈R，B．∃x0∈R，C．∀x∈R，x2+x+1＜0D．∀x∈R，x2+x+1≥03．（4分）设四边形ABCD的两条对角线为AC，BD，则“四边形ABCD为菱形”是“AC ⊥BD”的（）A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件4．（4分）对于任意实数a，b，c，d以下四个命题中，其中正确的有（）①ac2＞bc2，则a＞b，②若a＞b，c＞d，则a+c＞b+d；③若a＞b，c＞d，则ac＞bd；④若a＞b，则．A．4个B．3个C．2个D．1个5．（4分）已知正数x，y满足xy＝16，则x+y（）A．有最大值4B．有最小值4C．有最大值8D．有最小值8 6．（4分）如图，I是全集，M、P、S是I的3个子集，则阴影部分所表示的集合是（）A．（M∩P）∩S B．（M∩P）∪S C．（M∩P）∩∁I S D．（M∩P）∪∁I S 7．（4分）已知集合A＝{a﹣2，a2+4a，10}，若﹣3∈A，则实数a的值为（）A．﹣1B．﹣3C．﹣3或﹣1D．无解8．（4分）在“一带一路”知识测验后，甲、乙、丙三人对成绩进行预测．甲：我的成绩比乙高．乙：丙的成绩比我和甲的都高．丙：我的成绩比乙高．成绩公布后，三人成绩互不相同且只有一个人预测正确，那么三人按成绩由高到低的次序为（）A．甲、乙、丙B．乙、甲、丙C．丙、乙、甲D．甲、丙、乙二、填空题共8小题，每小题4分，共32分9．（4分）不等式组的解集为．10．（4分）若集合A＝{x||x﹣1|＜1}，B＝{x|x2﹣x＝0}，则A∪B＝．11．（4分）关于x的不等式ax2+bx+2＞0的解集是{x|﹣1＜x＜2}，则a+b＝．12．（4分）已知x＞1，当x＝时，则有最小值为．13．（4分）若不等式ax2+ax﹣1＞0的解集为∅，则实数a的取值范围是．14．（4分）已知集合A＝{x|＜0}，若1∉A，则实数a的取值范围为．15．（4分）已知集合A＝{x|x＜a}，B＝{x|x2﹣5x+4≥0}，若P：“x∈A”是Q：“x∈B”的充分不必要条件，则实数a的取值范围为．16．（4分）设a+b＝2019，b＞0，则当a＝时，+取得最小值．三、解答题共4小题，共36分。

【关键字】学期江西师大附中高一年级数学月考试卷命题人：吴小平审题人：黄润华2017.10一、选择题(本大题共12小题，每小题5分，共60分．每小题只有一个选项符合题意）1.设则下列结论中正确的是（）A. B. C. D.2. 已知集合，则=（）A. B. C. D.3. 已知全集则集合A的真子集共有（）个A. 3B.C. 8D. 74. 下列四个函数：（1），（2），（3），（4），其中定义域与值域相同的是（）A. （1）（2）B. （1）（2）（3）C. （1）（4）D. （1）（3）（4）5.若（）A. B. C. 3 D.36. 已知A,B是非空集合，定义，（）A. B. C. D.7. 已知函数上为增函数，则的取值范围是（）A. B. C. D.8. 设函数的值为（）A. aB. bC. a,b中较小的数D.a,b中较大的数9. 下列四个函数中，在上为增函数的是（）A. B. C. D.10. 设集合，则下列关系中成立的是（）A. B. C. D.11. 定义在[1,1]上的函数，则不等式的解集为（）A. B. C. D.12.设与是定义在同一区间上的两个函数，若对任意的都有则称和在上是“和谐函数”，区间为“和谐区间”，设在区间上是“和谐函数”，则它的“和谐区间”可以是（）A. B. C. D.二、填空题（本大题共4小题，每小题5分，共20分）13.已知集合若，则实数a的取值范围为.14. 函数的值域为.15. 已知集合A,B均为全集的子集，且=16. 已知函数恒成立，则实数m的取值范围为三、解答题（本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤）17. 设全集，集合，集合.求18. 已知全集（1）若，求实数q的取值范围；（2）若中有四个元素，求和q的值.19. 已知函数（1）若，试判断并用定义证明的单调性； （2）若，求的值域. 20. 已知函数（1）解不等式；（2）求在上的最大值. 21. 已知集合（1）若时，求实数a 的取值范围； （2）若时，求实数a 的取值范围. 22. 设二次函数满足下列条件：①对恒成立； ②对恒成立.（1）求的值； （2）求的解析式；（3）求最大的实数(1)m m >，使得存在实数t ，当[1,]x m ∈时，()f x t x +≤恒成立.高一数学10月考试答案13. [1,)-+∞ 14. 1[,)2+∞15. {}3 16. (3,)+∞17. 解：|1|221213x x x -<⇒-<-<⇒-<<,(1,3),(0,4)A B ∴=-=18.解：（1）A =∅，41329|,,1,,51525q q R q q q q ⎧⎫∈≠≠≠≠⎨⎬⎩⎭且；（2）45q =或1315q =或2925q =.19. 解：（1）当1a =时，9()|1|1[1,6]f x x x x =--+∈9911x x x x=--+=-递增证：任取12,[1,6]x x ∈且12x x < 则1221212121129()99()()()x x f x f x x x x x x x x x --=--+=--=21129()[1]0x x x x -+> 21()()()f x f x f x ∴>∴在[1,6]上单调递增.（2）当8a =时，999()|8|88816()f x x x x x x x=--+=--+=-+令9t x x=+[1,6]x ∈[6,10]t ∴∈()16[6,10]f x y t ∴==-∈ 所以()f x 的值域为[6,10].20. 解：（1）2()()|2||4|(2)4x f x g x x x x x x x ≥⎧>⇒->+⇔⎨->+⎩或42(2)4x x x x -≤<⎧⎨->+⎩或4(2)4x x x x <-⎧⎨---⎩22340x x x ≥⎧⇒⎨-->⎩或24240x x x -≤<⎧⎨-+<⎩或24340x x x <-⎧⎨--<⎩ 214x x x ≥⎧⇒⎨<->⎩或或42x x φ-≤<⎧⎨∈⎩或414x x <-⎧⎨-<<⎩4x ⇒>（2）222(2)()|2|2(2)x x x f x x x x x x ⎧-≥⎪=-=⎨-+<⎪⎩①当01a <<时，2()()2f x f a a a ==-+大②当11a ≤≤()(1)1f x f ==大③当1a >2()()2f x f a a a ==-大21.解：{}0(,2)(1,2),|()(2)00(2,)0a B a a A B x x a x a a B a a a B φ>=⎧⎪==--<⇒<=⎨⎪==⎩当时当时当时（1）01122a A B a a a >⎧⎪⊆⇒≤⇒=⎨⎪≥⎩由已知得（2）当A B =∅时若0a A B ≤=∅时，1022122a A B a a a a >=∅≥≤⇒≥≤时，使，则或或 综上：122a a ≥≤或22.解：（1）当x=1时，1(1)1(1)1f f ≤≤⇒=（2）由已知可得()1,122b f x x b a a=-∴-=-⇒=的轴……①由(1)11f a b c =⇒++=……②由()f x x ≥恒成立2(21)130ax a x a ⇒+-+-≥对R 恒成立则201(21)4(13)04a a a a a >⎧⎪⎨∆=---≤⇒=⎪⎩由22211()1)2131)22f x x ax ax a x ≤+⇒++-≤+（恒成立（对x R ∈恒成立2(21)4160a x ax a ⇒-++-≤恒成立则2221012164(21)(16)01(41)04a a a a a a a -<⎧⎪⎧⎪<⎪⎨⎪∆=---≤⇒⎨⎪⎪⎪-≤⇒=⎪⎩⎩131,1244b c ∴==-=,221111()(1)4244f x x x x ∴=++=+ （3）21()(1),()[1,]4f x t x t f x t x m ∴+=+++≤使在恒成立，则使()y f x t =+的图像在y x =的下方，且m 最大，则1，m 为()f x t x +=的两个根 由21(1)1(2)1044f t t t t +=⇒+=⇒==-或此文档是由网络收集并进行重新排版整理.word 可编辑版本！。

江西师大附中高三年级数学（理）月考试卷（2012.10）一、选择题（本大题共10小题，每小题5分，共50分，每小题只有一个选项是正确） 1．若集合{}(,)cos ,A x y y x x R ==∈，{}ln B x y x ==，则A B =（ ） A ．{}|11x x -≤≤ B ．{}|0x x ≥C ．{}01x x <≤ D ．∅ 2．已知复数z ，映射zi z f →:，则i 32+的原象是（ ）A ．i 23-B ．i 32-C ．i 23+D ．i 32+3．已知,a b R Î，则33log log a b >是 11()()22ab<的（ ） A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件 4．命题“20,10x R x ax ∃∈++<使”的否定是（ ）A ．20,10x R x ax ∃∈++>使B ．20,10x R x ax ∃∈++≥使C ．2,10x R x ax ∀∈++>成立D ．2,10x R x ax ∀∈++≥成立5．若函数()sin ()f x x x x R ωω=∈，又()2,()0f f αβ=-=，且βα-的最小值为34π，则正数ω的值是（ ） A ．13B ．23C ．43D ．326．已知A ，B ，C 三点的坐标分别是(3,0)A ，(0,3)B ，(cos ,sin )C αα，3,22ππα⎛⎫∈⎪⎝⎭，若1AC BC ⋅=-，则21tan 2sin sin 2ααα++的值为（ ）A ．59-B ．95- C ．2D ．37．如图，正方形ABCD 的顶点A (0，B，0），顶点C ，D位于第一象限，直线:(0l x t t =≤将正方形ABCD 分成两部分，记位于直线l 左侧阴影部分的面积为()f t ，则函数()S f t =的图象大致是（ ）A B C D8．已知函数31,(1)12()111,(0)6122x x x f x x x ⎧<≤⎪⎪+=⎨⎪-+≤≤⎪⎩和函数()sin 1(0)6g x a x a a π=-+>，若存在[]12,0,1x x ∈，使得12()()f x g x =成立，则实数a 的取值范围是（ ） A ．13,22⎛⎤⎥⎦⎝ B ．[1,2)C ．1,22⎡⎤⎢⎥⎣⎦D ．31,2⎡⎤⎢⎥⎣⎦9．已知()y f x =为R 上的可导函数，当0x ≠时，()()'0f x f x x+>，则关于x 的函数()()1g x f x x=+的零点个数为（ ） A ．1 B ．2 C ．0 D ．0或 2 10．已知)(x f y =是偶函数，而)1(+=x f y 是奇函数，对任意12,[0,1]x x ∈，且12x x ≠时,有12120()()x x f x f x ->-,则)15106(),17101(),1998(f c f b f a ===的大小关系是（ ） A ．c a b << B ．c b a << C ．a c b << D ．a b c <<二、填空题（本大题共5小题，每小题5分，共20分）11．如图，在一个长为π，宽为2的矩形OABC 内，曲线sin (0)y x x π=≤≤与x 轴围成如图所示的阴影部分，向矩形OABC 内随机投一点(该点落在矩形OABC 内任何一点是等可能的)，则所投的点落在阴影部分的概率是 .12．在△ABC 中，角A 、B 、C 的对边分别为a 、b 、c ,若(222a cb +-)tan B =,则B 的值为 .13．若,,a b c 均为单位向量，且0a b ⋅= ，()()0a c b c -⋅-≤，则a b c +- 的最大值为 .14．函数()f x 的定义域为D ，若对于任意12,x x D ∈，当12x x <时，都有12()()f x f x ≤，则称函数()f x 在D 上为非减函数.设函数()f x 为定义在[0，1]上的非减函数，且满足以下三个条件：①(0)0f =；② (1)()1f x f x -+=，[]0,1x ∈； ③ 当x ∈10,4⎡⎤⎢⎥⎣⎦时，()2f x x ≥恒成立.则315()729f f f ⎛⎫⎛⎫++= ⎪ ⎪⎝⎭⎝⎭.15．关于x 的方程()2224440x x k ---+=，给出下列四个命题：①存在实数k ，使得方程恰有2个不同的实根； ②存在实数k ，使得方程恰有4个不同的实根； ③存在实数k ，使得方程恰有5个不同的实根； ④存在实数k ，使得方程恰有6个不同的实根; ⑤存在实数k ，使得方程恰有8个不同的实根．其中真命题的序号是 （写出所有真命题的序号）.三、解答题（本大题共6小题，共75分．解答应写出文字说明、证明过程或演算步骤）16．（本小题共12分）设函数24()cos(2)2cos 3f x x x π=-+. （1）求()f x 的最大值，并写出使()f x 取得最大值的x 的集合； （2）在ABC ∆中，角A 、B 、C 的对边分别为a b c 、、，若3(),2,2f B C b c +=+= 求a 的最小值.17．（本小题共12分）师大附中高三年级学生为了庆祝第28个教师节，同学们为老师制作了一大批同一种规格的手工艺品，这种工艺品有A 、B 两项技术指标需要检测，设各项技术指标达标与否互不影响，若A 项技术指标达标的概率为3,4B 项技术指标达标的概率为89，按质量检验规定：两项技术指标都达标的工艺品为合格品. （1）求一个工艺品经过检测至少一项技术指标达标的概率；（2）任意依次抽取该工艺品4个，设ξ表示其中合格品的个数，求ξ的分布列及E ξ. 18．（本小题共12分）已知等比数列{}n a 满足13223a a a +=，且32a +是24,a a 的等差中项. （1）求数列{n a ｝的通项公式； （2）若2121log ,,n n n n nb a S b b b a =+=+++ 求使12470n n S +-+<成立的正整数n 的最小值.19．（本小题共12分）如图边长为4的正方形ABCD 所在平面与正PAD ∆所在平面互相垂直，M Q 、分别为,PC AD 的中点. （1）求证：//PA 平面MBD ；（2）求：二面角P BD A --的余弦值；（3）试问：在线段AB 上是否存在一点,N 使得平面PCN ⊥平面?PQB 若存在，试指出点N 的位置，并证明你的结论；若不存在，请说明理由.20．（本小题共13分）已知抛物线24x y =的焦点是椭圆 2222:1(0)x y C a b a b+=>>一个顶点，椭圆C O （1）求椭圆C 和圆O 的方程；（2）已知00(,)M x y 是圆O 上任意一点，过M 点作直线12,l l ，使得12,l l 与椭圆C 都只有一个公共点，求证：12l l ⊥.21．（本小题共14分）已知函数()ln f x x =，3()2ag x x=-，（a 为实数）.（1）当1a =时，求函数()()()x f x g x ϕ=-在[4,)x ∈+∞上的最小值；（2）若方程()2()f x e g x =（其中 2.71828e = ）在区间1[,1]2上有解，求实数a 的取值范围；（3）证明：*151[2(21)()(1)]21,.460nk n f k f k f k n n N =+<+--+<+∈∑（参考数据：ln 20.6931)≈.江西师大附中高三年级数学（理）答题卷一、选择题：(本大题共10小题，每小题5分，共50分)．二、填空题（本大题共5小题，每题5分，共25分） 11． 1π12．3π、23π 13． 114．3215．①②③⑤三、解答题（本大题共6小题，共75分，要有适当的解答过程） 16．（本小题共12分） 设函数24()cos(2)2cos 3f x x x π=-+ （1）求()f x 的最大值，并写出使()f x 取得最大值的x 的集合 （2）在ABC ∆中，角A 、B 、C 的对边分别为a b c 、、，若3(),2,2f B C b c +=+= 求a 的最小值 解：（1）24()cos(2)2cos 3f x x x π=-+ 44cos 2cos sin 2sin33x x ππ=+cos 21x ++1cos 221cos(2)123x x x π=+=++ ∴当22(),3x k k Z ππ+=∈即()6x k k Z ππ=-∈时，()f x 取得最大值2，故使()f x 取得最大值的x 的集合为{|,}6x x k k Z ππ=-∈（2）由题意知3()cos[2()]1,32f B C B C π+=+++=即1cos(22)32A ππ-+=1cos(2)32A π∴-=5(0,),2(,),333A A ππππ∴∈∴-∈-2,333A A πππ∴-=∴=在ABC ∆中，由余弦定理得2222222312cos ()3()()()44a b c bc A b c bc b c b c b c =+-=+-≥+-+=+又22,1,1b c a a +=∴≥∴≥当且仅当1b c ==时，a 取得最小值1 17．（本小题共12分）师大附中高三年级学生为了庆祝第28个教师节，同学们为老师制作了一大批同一种规格的手工艺品，这种工艺品有A 、B 两项技术指标需要检测，设各项技术指标达标与否互不影响，若A 项技术指标达标的概率为3,4B 项技术指标达标的概率为89，按质量检验规定：两项技术指标都达标的艺术品为合格品（1）求一个工艺品经过检测至少一项技术指标达标的概率（2）任意依次抽取该工艺品4个，设ξ表示其中合格品的个数，求ξ分布列及E ξ 解（1）设:M 一个工艺品经过检测至少一项技术指标达标，则:,M A B 都不达标，故1135()1()14936P M P M =-=-⨯=（2）依题意知2(4,),3B ξ411(0)381P ξ⎛⎫=== ⎪⎝⎭1314218(1)3381P C ξ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭ ()2224212423381P C ξ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭ ()334213233381P C ξ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭ ()42164381P ξ⎛⎫=== ⎪⎝⎭433E ξ=⋅= 18．（本小题共12分）已知等比数列{}n a 满足13223,a a a +=且32a +是24,a a 的等差中项 （1）求数列{n a ｝的通项公式（2）若2121log ,,n n n n nb a S b b b a =+=+++ 求使12470n n S +-+<成立的正整数n 的最小值解（1）设等比数列{n a ｝的公比为q由13224323,2(2)a a a a a a +=⎧⎨+=+⎩得2113211(2)3()24a q a q a q q a q ⎧+=⎪⎨+=+⎪⎩①②由①得2320,q q -+=解得1q =或2q = 当1q =时，不合题意舍去当2q =时，代入②得12,a =则1222n n n a -=⋅= （2）因为2211log 2log 2,2n n n n n n b a n a =+=+=- 所以23132122232n n n n S b b b b n =++++=-+-+-++-=232(12)(1)(2222)(123)122n nn n n -+++++-++++=-=-12112222n n n +---因为12470,n n S +-+<所以1211122247022n n n n ++----+<即2900n n +->，解得9n >或10n <-又*N n ∈，故使12470n n S +-+<成立的正整数n 的最小值为1019．（本小题共12分）如图边长为4的正方形ABCD 所在平面与正PAD ∆所在平面互相垂直，M Q 、分别为,PC AD 的中点（1）求证：//PA 平面;MBD (2)求二面角P BD A --的余弦值；（3）试问：在线段AB 上是否存在一点,N 使得平面PCN ⊥平面?PQB 若存在，试指出点N 的位置，并证明你的结论；若不存在，请说明理由（1）证明：连接AC 交BD 于点O ，连接,MO 由正方形ABCD 知O 为AC 的中点，M为PC 的中点，//MO PA ∴MO ⊂ 平面,MBD PA ⊄平面,//MBD PA ∴平面MBD（2）二面角P BD A --（3）解，存在点,N 当N 为AB 中点时，平面PQB ⊥平面PNC∴四边形ABCD 是正方形，Q 为AD 的中点，.BQ NC ∴⊥由（1）知，PQ ⊥平面,,,ABCD NC ABCD PQ NC ⊂∴⊥平面 又,BQ PQ Q NC PQB ⋂=∴⊥平面,NC PCN PCN PQB ⊂∴⊥ 平面平面平面20．（本小题共13分）已知抛物线24x y =的焦点是椭圆2222:1(0)x y C a b a b+=>>一个顶点，椭圆C 的离心率为，另有一圆O （1）求椭圆C 和圆O 的方程（2）已知00(,)M x y 是圆O 上任意一点，过M 点作直线12,l l ，使得12,l l 与椭圆C 都只有一个公共点，求证：12l l ⊥解（1）由24x y =可得抛物线焦点坐标为（0，1），由已知得1b =，又222223,,4c e a b c a =∴==+得24,a ==∴椭圆C 的方程为2214x y +=，圆O 的方程为225x y +=（2）若点M 的坐标为(2,1).(2,1),(2,1),(2,1)----，则过这四点分别作满足条件的直线12,l l ，若一条直线斜率为0,则另一条斜率不存在，则12l l ⊥若直线12,l l 斜率都存在，则设过M 与椭圆只有一个公共点的直线方程为00(),y y k x x -=-由0022()14y kx y kx x y =+-⎧⎪⎨+=⎪⎩得22004[()]4x kx y kx ++-=即2220000(14)8()4()40k x k y kx x y kx +-+-⋅+--= 则2220000[8()]4(14)[4()4]0k y kx k y kx ∆=--+--=化简得2220000(4)210x k x y k y -++-= 又22005,x y +=2220000(4)240x k x y k x ∴-++-=设直线12,l l 的斜率分别为12,k k ，因为12,l l 与椭圆都只有一个公共点，所以12,k k 满足2220000(4)240x k x y k x -++-= 201212241,4x k k l l x -∴⋅==-∴⊥- 21．（本小题共14分）已知函数()ln f x x =，3()(2ag x a x=-为实数） （1）当1a =时，求函数()()()x f x g x ϕ=-在[4,)x ∈+∞上的最小值； （2）若方程()2()f x e g x =（其中 2.71828e = ）在区间1[,1]2上有解，求实数a 的取值范围；（3）证明：*151[2(21)()(1)]21,.460nk n f k f k f k n n N =+<+--+<+∈∑（参考数据：ln 20.6931)≈解（1）当1a =时，13()()()ln ,2x f x g x x x ϕ=-=+- 22111'(),x x x x xϕ--=+=令'()0,0,x x ϕ>>又得1x > ()x ϕ∴在(0,1]上单调递减，在[1,)+∞上单调递增 4x ∴≥时135()(4)ln 4ln 4.424x ϕϕ≥=+-=- ()x ϕ∴的最小值为5ln 44-（2）2()()f x e g x =在1[,1]2x ∈上有解2ln 32xa e x ⇔=-在1[,1]2x ∈上有解332a x x ⇔=-在1[,1]2x ∈上有解令331(),[,1]22h x x x x =-∈ 2231'()33()22h x x x =-=-令'()0,0,02h x x x >><<又解得 331()[,]222h x x x x ∴=-∈在上单调递增，[2x ∈上单调递减，又1(1)().(1)()2h h h h x h <∴<≤即1()2h x ≤≤故1[2a ∈（3）设2(21)()(1)k a f k f k f k =+--+=24412ln(21)ln ln(1)ln(1)k k k k k k k +++--+=+ 由（1），可得min 5()ln 40(4),4x x ϕ=->≥ 31ln (4)2x x x∴>-≥ 24414(1)k k k k ++>+223(1)5115115111().244144(21)44(21)(23)482123k k k a k k k k k k k +∴>-=+⋅>+⋅=+-+++++++1511111115111483557212348323nk k a n n n n n =⎛⎫⎛⎫∴>+-+-++-=+- ⎪ ⎪+++⎝⎭⎝⎭∑511151=.4835460n n ⎛⎫≥+-+ ⎪⎝⎭ 构造函数()F x ()11ln 24,'()1,xx x x F x x x-=-+≥=-=当4x ≥时，1'()0,()xF x F x x-=<∴在[4,)+∞上单调递减， 即()(4)ln 422(ln 21)0F x F ≤=-=-<∴当4x >时，ln 2x x <-1111ln(4)4211k a k k k k ∴=+-<+--++即1121k a k k <+-+1121211nk k a n n n =∴<+-<++∑ 故*151[2(21)()(1)]21,460nk n f k f x f k n n N =+<+-=+<+∈∑。

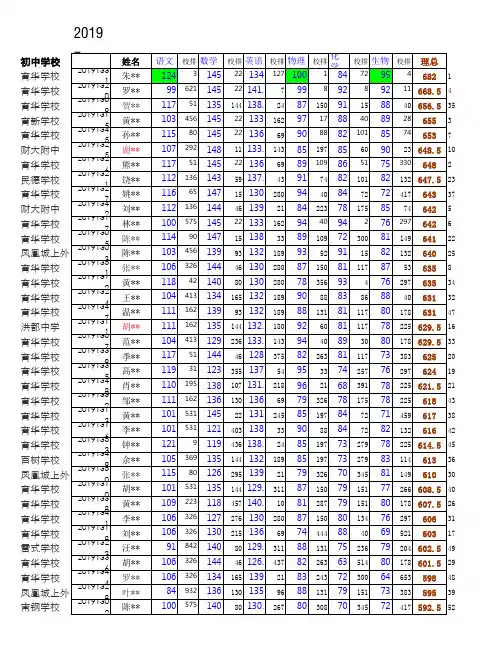
2023北京首都师大附高一10月月考数 学第Ⅰ卷（共50分）一、选择题（本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，选出符合题目要求的一项）1. 下列各式：①{}10,1,2∈；②{}0,1,2∅⊆；③{}{}10,1,2∈；④{}{}0,1,22,0,1=，其中错误的个数是（ ） A. 1个B. 2个C. 3个D. 4个2. 命题“2x ∃<,220x x −<”的否定是（ ） A. 2x ∃≤,220x x −≥ B. 2x ∀≥,02x << C. 2x ∃<,220x x −≥D. 2x ∀<,0x ≤或2x ≥3. 将下列多项式因式分解，结果中不含因式()2x +的是（ ） A. 224x x + B. 2312x −C. 26x x +−D. ()()228216x x −+−+4. 若集合{}{3},21,Z A xx B x x n n =<==+∈∣∣，则A B =（ ）A. ()1,1−B. ()3,3−C. {}1,1−D. {}3,1,1,3−−5. 如图，I 是全集，M 、P 、S 是I 的3个子集，则阴影部分所表示的集合是（ ）A. ()M P SB. ()M P SC. ()M P SD. ()M P S6. 已知p ：111x <+，q ：()10x x +<，则p 是q 的（ ）A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件7. 下列结论成立的是（ ） A. 若ac bc <，则a b > B. 若a b >，则22a b > C. 若a b >，则11a b< D. 若110a b<<，则0b a <<8. 设集合11,Z ,,Z 3663k k M x x k N x x k ⎧⎫⎧⎫==+∈==+∈⎨⎬⎨⎬⎩⎭⎩⎭||，则（ ） A. MNB. M NC. N MD. M N ⋂=∅9. 已知,,A B C 是三个集合，若A B B C ⋃=⋂，则一定有（ ） A. A C ⊆B. C A ⊆C. C A ≠D. A =∅10. 设()C M 表示非空集合M 中元素的个数，已知非空集合,A B .定义()(),()()()(),()()C A C B C A C B A B C B C A C A C B −≥⎧⊗=⎨−<⎩，若{}1,2A =，()(){}2220B x x ax x ax =+++=且1A B ⊗=，则实数a 的所有取值为（ ）A. 0B. 0，−C. 0，D. −，0，第Ⅱ卷（共70分）二、填空题（本大题共5小题，每小题5分，共25分）11. 方程组322327x y x y +=⎧⎨−=⎩的解集用列举法表示为______________.12. 若“25x m >−”是“|x |<1”的必要不充分条件，则实数m 的取值范围是___________ 13. 设a ，b ∈R ，集合{}2,0,1{,,0}a a b −=，则a b +的值是______.14. 已知集合{}|3A x a x =≤≤，{}|0B x x =<，若A B ⋂=∅，则实数a 的取值范围是______． 15. 当两个集合中有一个集合为另一个集合的子集时，称两个集合之间构成“全食”；当两个集合有公共元素，但互不为对方子集时，称两个集合之间构成“偏食”，对于集合11,,12A ⎧⎫=−⎨⎬⎩⎭，{}2B x x a ==|.若A 与B 构成“全食”，则a 的取值范围是______；若A 与B 构成“偏食”，则a 的取值范围是______.三、解答题（本大题共4小题，共45分.解答应写出文字说明，演算步骤或证明过程）16. 已知全集U =R ，集合{R |211}A x x =∈−≤，集合{R |12}B x x =∈−<≤． （1）求集合A B ⋂及()UA B ⋃；（2）若集合{|2,0}=∈≤<>C x R a x a a ，且C B ⊆，求实数a 的取值范围． 17. 已知关于x 的一元二次方程()22230x m x m +−+=有两个实数根1x ，2x .（1）求实数m 的取值范围； （2）若12126x x x x +=−，求m 的值.18. 已知全集U =R ，812x A xx ⎧⎫+=>⎨⎬−⎩⎭，{}22240B x x mx m =−+−<，{}14C x x =−<<，在①Ux A ∈；②x A C ∈；③x A C ∈⋃；这三个条件中任选一个补充到下列问题中并作答.问题：设p ：______，q ：x B ∈，是否存在实数m ，使得p 是q 的必要不充分条件？若实数m 存在，求m 的取值范围；若实数m 不存在，说明理由.19. 已知集合{}1,2,,A n =⋅⋅⋅（3n ≥），表示集合A 中的元素个数，当集合A 的子集i A 满足2i A =时，称i A 为集合A 的二元子集，若对集合A 的任意m 个不同的二元子集1A ，2A ，…，m A ，均存在对应的集合B 满足：①BA ⊆；②B m =；③1i BA ≤（1i m ≤≤），则称集合A 具有性质J .（1）当3n =时，若集合A 具有性质J ，请直接写出集合A 的所有二元子集以及m 的一个取值； （2）当6n =，4m =时，判断集合A 是否具有性质J ？并说明理由.参考答案第Ⅰ卷（共50分）一、选择题（本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，选出符合题目要求的一项）1. 【答案】A【分析】根据集合与集合的关系，元素与集合的关系即可求解.【详解】由元素与集合的关系可知{}10,1,2∈正确，{}{}10,1,2∈不正确， 由集合之间的关系知{}0,1,2∅⊆正确， 由集合中元素的无序性知{}{}0,1,22,0,1=正确， 故错误的个数为1， 故选：A【点睛】本题主要考查了元素与集合的关系，集合的子集，集合的相等，属于容易题. 2. 【答案】D【分析】根据存在量词命题的否定是全称量词命题即可得到结果. 【详解】命题“2x ∃<,220x x −<”是存在量词命题, 又22002x x x −<⇒<<,所以其否定为全称量词命题,即为“2x ∀<,0x ≤或2x ≥”. 故选:D. 3. 【答案】C【分析】利用提取公因式法判断A ，利用公式法判断B ，利用十字相乘法判断C 、D. 【详解】对于A.原式()22x x =+，不符合题意；对于B.原式()()()234322x x x =−=+−，不符合题意；对于C 原式()()23x x =−+，符合题意； 对于D.原式()()22242x x =−+=+，不符合题意. 故选：C. 4. 【答案】C【分析】解绝对值不等式得A ，根据交集的定义计算即可.【详解】解3x <得33x −<<，即()3,3A =−，B 为奇数集，故{}1,1A B =−.故选：C 5. 【答案】C【分析】根据Venn 图表示的集合运算作答．【详解】阴影部分在集合,M P 的公共部分，但不在集合S 内，表示为()⋂⋂M P S ， 故选：C ． 6. 【答案】D【分析】分别求出,p q ，再分析出,p q 的推导关系. 【详解】()11110010111x x x x x x −<⇒−<⇒<⇒+>+++， 所以:0p x >或1x <−，而:10q x −<<，所以p 是q 的既不充分也不必要条件， 故选：D 7. 【答案】D【分析】根据不等式的性质或举出反例对各选项逐一判断即可.【详解】选项A ：当0c >时，若ac bc <，则a b <，当0c <时，若ac bc <，则a b >，故A 说法错误； 选项B ：若1a =，2b =−满足a b >，此时22a b <，故B 说法错误； 选项C ：当0a b >>或0a b >>时， 11a b <，当0a b >>时， 11a b>，故C 说法错误；选项D ：当110a b<<时，0ab >，所以不等式同乘ab 可得0b a <<，故D 说法正确； 故选：D 8. 【答案】B【分析】根据集合,M N 的表达式，可求出集合M 是16的奇数倍，N 是16的整数倍，即可得出,M N 的关系.【详解】由()11,Z 21,Z 366k M x x k x x k k ⎧⎫⎧⎫==+∈==+∈⎨⎬⎨⎬⎩⎭⎩⎭||可知，集合M 表示的是16的奇数倍； 由()11,Z 2,Z 636k N x x k x x k k ⎧⎫⎧⎫==+∈==+∈⎨⎬⎨⎬⎩⎭⎩⎭||可知，集合N 表示的是16的整数倍； 即可知M 是N 的真子集，即M N . 故选：B 9. 【答案】A 【分析】根据()B C B ⋂⊆，以及()B C C ⋂⊆，结合已知条件，即可判断集合之间的关系. 【详解】因为()B C B ⋂⊆，又A B B C ⋃=⋂， 故可得()A B B ⋃⊆，则A B ⊆； 因为()B C C ⋂⊆，又A B B C ⋃=⋂,故可得()A B C ⋃⊆，则B C ⊆； 综上所述：A B C ⊆⊆. 故选：A.【点睛】本题考查由集合的运算结果，求集合之间的关系，属基础题. 10. 【答案】D【分析】由题意可得集合B 中的元素个数为1个或3个，分集合B 中的元素个数为1和集合B 中的元素个数为3两种情况，再结合一元次方程根的个数求解即可. 【详解】解：由2220xax x ax 可得20x ax或220x ax ++=，又因为{}1,2A =，1A B ⊗=， 所以集合B 中的元素个数为1个或3个， 当集合B 中的元素个数为1时，则20x ax有两相等的实数根，且220x ax ++=无解，所以22080a a ⎧=⎨−<⎩，解得0a =；当集合B 中的元素个数为3时，则20x ax有两不相等的实数根，且220x ax ++=有两个相等且异于方程20x ax 的根的解，所以20Δ80a a ≠⎧⎨=−=⎩，解得a =a =−综上所述，0a =或a =a =− 故选：D.【点睛】关键点睛：本题的关键是根据题意得出集合B 中的元素个数为1个或3个.第Ⅱ卷（共70分）二、填空题（本大题共5小题，每小题5分，共25分）11. 【答案】(){}3,7−【分析】首先根据方程组求出其解，然后运用列举法表示出对应的解集即可（以有序数对(),a b 的形式表示元素）.【详解】因为322327x y x y +=⎧⎨−=⎩，所以37x y =⎧⎨=−⎩，所以列举法表示解集为：(){}3,7−.故答案为(){}3,7−.【点睛】本题考查二元一次方程组解集的列举法表示，难度较易.二元一次方程组的解用列举法表示时，可将元素表示成有序数的形式：(),x y . 12. 【答案】(],2−∞【分析】根据题意得到(1,1)− (25,+)m −∞，再利用数轴得到不等式，解出不等式即可. 【详解】||<1,1<<1x x ∴−>25x m −是||1x <的必要不充分条件,(1,1)∴− (25,+)m −∞,251,2m m ∴−≤−∴≤, ∴实数m 的取值范围是(,2]−∞,故答案为： (,2]−∞. 13. 【答案】0【分析】由集合相等的含义，分类讨论元素对应关系即可. 【详解】由集合元素互异性：0a ≠，又{}2,0,1{,,0}a a b −=，则21a a b ⎧=⎨=−⎩或21a ba ⎧=⎨=−⎩，解得11a b =⎧⎨=−⎩或11a b =−⎧⎨=⎩，故0a b += 故答案为：0 14. 【答案】0a ≥【分析】分别讨论A =∅和A ≠∅两种情况求解.【详解】因为A B ⋂=∅， 若3a >，则A =∅，满足题意；若3a ≤，则应满足0a ≥，所以03a ≤≤， 综上，0a ≥. 故答案为：0a ≥.15. 【答案】 ①. {|0a a <或}1a = ②. 14⎧⎫⎨⎬⎩⎭【分析】分情况解集合B ，再根据“全食”与“偏食”的概念分析集合中元素满足的关系列式求解即可. 【详解】由{}2B x x a ==|可知，当a<0时，B =∅，此时B A ⊆； 当0a =时，{}0B =，此时A B ⋂=∅，当0a >时，{B =； 又11,,12A ⎧⎫=−⎨⎬⎩⎭，若A 与B 构成“全食”，则B A ⊆， 当a<0时，满足题意；当0a =时，不合题意；当0a >时，要使B A ⊆，则{}1,1B =−1=，解得1a =； 综上，A 与B 构成“全食”时，a 的取值范围是{|0a a <或}1a =； 若A 与B 构成“偏食”时，显然0a ≤时，不满足题意，当0a >时，由A B ⋂≠∅，所以11,22B ⎧⎫=−⎨⎬⎩⎭12=，解得14a =，此时a 的取值范围是14⎧⎫⎨⎬⎩⎭.故答案为：{|0a a <或}1a =；14⎧⎫⎨⎬⎩⎭三、解答题（本大题共4小题，共45分.解答应写出文字说明，演算步骤或证明过程）16. 【答案】（1）(1,1]A B ⋂=−，(1,)UA B ⋃=−+∞；（2）(0,1]【分析】（1）解一元一次不等式求集合A ，再应用集合的交并补运算求A B ⋂及()UA B ⋃.（2）由集合的包含关系可得2a ≤2，结合已知即可得a 的取值范围． 【小问1详解】由211x −≤得：1x ≤，所以(,1]A ∞=−，则(1,)UA =+∞，由(1,2]B =−，所以(1,1]A B ⋂=−，(1,)UA B ⋃=−+∞．【小问2详解】 因为C B ⊆且0a >， 所以2a ≤2，解得1a ≤． 所以a 的取值范围是(0,1]． 17. 【答案】（1）34m ≤ （2）1m =−【分析】（1）根据根的判别式列不等式，然后解不等式即可；（2）根据韦达定理得到1223x x m +=−+，212x x m =，然后代入求解即可.【小问1详解】因为有两个实根，所以()222341290m m m ∆=−−=−+≥，解得34m ≤. 【小问2详解】由题意得()122323x x m m +=−−=−+，212x x m =，所以2236m m −+=−，整理得 ()()310m m −+=，解得3m =或-1，因为34m ≤，所以1m =−. 18. 【答案】答案见解析【分析】分别求解集合,A B ，并求解三个条件的集合，再根据必要不充分条件，转化为集合的包含关系，即可列式求解. 【详解】不等式8831100222x x x x x x +++>⇔−>⇔<−−−，即()()320x x +−<， 解得：32x −<<，即{}32A x x =−<<，()()22240220x mx m x m x m −+−<⇔−−−+<⎡⎤⎡⎤⎣⎦⎣⎦，解得：22m x m −<<+，即{}22B x m x m =−<<+， 若选①，{3UA x x =≤−或2}x ≥，:p {3U x A x x ∈=≤−或2}x ≥，{}:22q x B x m x m ∈=−<<+，若p 是q 的必要不充分条件，则BUA ,即23m +≤−或22m −≥，解得：5m ≤−或4m ≥；所以存在实数m ，使得p 是q 的必要不充分条件，m 的范围为5m ≤−或4m ≥； 若选②，{}12A C x x ⋂=−<<，:p {}12x A C x x ∈⋂=−<<，{}:22q x B x m x m ∈=−<<+，若p 是q 的必要不充分条件，则B ()A C ,则2122m m −≥−⎧⎨+≤⎩，解集为∅；所以不存在实数m ，使得p 是q 的必要不充分条件； 若选③，{}34A C x x ⋃=−<<，:p {}34x A C x x ∈⋃=−<<，{}:22q x B x m x m ∈=−<<+，若p 是q 的必要不充分条件，则B ()A C ,则2324m m −≥−⎧⎨+≤⎩，解得：12m −≤≤；所以存在实数m ，使得p 是q 的必要不充分条件，m 的取值范围为12m −≤≤； 19. 【答案】（1）答案见解析 （2）不具有，理由见解析【分析】（1）根据集合A 具有性质J 的定义即可得出答案；（2）当6n =，4m =时，利用反证法即可得出结论. 【小问1详解】当3n =时，{}1,2,3A =，集合A 的所有二元子集为{}{}{}1,2,1,3,2,3，则满足题意得集合B 可以是{}1或{}2或{}3，此时1m =， 或者也可以是{}1,2或{}1,3或{}2,3，此时2m =； 【小问2详解】当6n =，4m =时，{}1,2,3,4,5,6A =，假设存在集合B ，即对任意的()1234,,,,4,114i A A A A B B A i =⋂≤≤≤，则取{}{}{}{}12341,2,3,4,5,6,2,3A A A A ====，（4A 任意构造，符合题意即可） 此时由于4B =，由抽屉原理可知，必有()223i B A i ⋂=≤≤， 与题设矛盾，假设不成立， 所以集合A 是不具有性质J .【点睛】关键点点睛：此题对学生的抽象思维能力要求较高，特别是对数的分析，在解题时注意对新概念的理解与把握是解题的关键.。

江西师大附中高三10月月考试卷理科数学一、选择题(本大题共12小题，每小题5分，共60分．每小题只有一个选项符合题意．）1.设复数，其中是实数，是虚数单位，若，则复数在复平面内对应的点位于（）A. 第一象限B. 第二象限C. 第三象限D. 第四象限2.已知集合，集合，则集合（）A. B. C. D.3.已知向量与的夹角是，且，若，则实数λ的值为（）A. B. C. D.4.下列命题中的假命题是（）A. B. C. D.5.曲线在处的切线的倾斜角是（）A. B. C. D.6.函数的图像可能是（）A. B.C. D.7.函数，若，则的值是（）A. B. 或 C. D. 或8.已知函数，给出下列四个结论：（）①函数的最小正周期是；②函数在区间上是减函数；③函数图像关于对称；④函数的图像可由函数的图像向右平移个单位，再向下平移1个单位得到．其中正确结论的个数是A. 1B. 2C. 3D. 49.定义在上的函数满足，若在上是增函数，记，则（）A. B. C. D.10.已知的内角所对的边分别是，，则“”是“有两解”的（）A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件11.如图，在中，已知，点为的三等分点（靠近点），则的取值范围为（）A. B. C. D.12.已知是定义在上的可导函数，且满足，则（）A. B. C. 为减函数 D. 为增函数二、填空题(本大题共4小题，每小题5分，共20分．）13.____________．14.如图所示，在中，，是上的一点，若则，实数的值为________________．15.已知函数，若存在两个不相等的实数，使得（其中为自然对数的底数），则实数的取值范围为_____________．16.在锐角中，角的对边分别为，，，则的取值范围是_____________．三、解答题（本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤）17.已知函数，数列满足．（1）求数列的通项公式；（2）令，若对一切成立，求最小正整数．18.如图，四棱锥的底面为平行四边形，，．（1）求证：；（2）若，，，求平面与平面所成角的余弦值．19.“过大年，吃水饺”是我国不少地方过春节的一大习俗．2018年春节前夕，市某质检部门随机抽取了100包某种品牌的速冻水饺，检测其某项质量指标，检测结果如频率分布直方图所示．（1）求所抽取的100包速冻水饺该项质量指标值的样本平均数（同一组中数据用该组区间的中点值作代表）；（2）①由直方图可以认为，速冻水饺的该项质量指标值服从正态分布，利用该正态分布，求落在内的概率；②将频率视为概率，若某人从某超市购买了4包这种品牌的速冻水饺，记这4包速冻水饺中这种质量指标值位于内的包数为，求的分布列和数学期望．附：①计算得所抽查的这100包速冻水饺的质量指标的标准差为；②若，则，．20.已知椭圆：的离心率为，且以两焦点为直径的圆的内接正方形面积为2．（1）求椭圆的标准方程；（2）若直线：与椭圆相交于，两点，在轴上是否存在点，使直线与的斜率之和为定值？若存在，求出点坐标及该定值，若不存在，试说明理由．21.设，函数（1）若无零点，求实数的取值范围；（2）若有两个相异零点，求证：．22.已知曲线的参数方程为，在极坐标系中曲线的极坐标方程为．（1）求曲线的普通方程与曲线的直角坐标方程；（2）若曲线与曲线交于两点，求．23.设函数．（1）若的最小值是，求的值；（2）若对于任意的实数，总存在，使得成立，求实数的取值范围．江西师大附中高三10月月考试卷理科数学解析一、选择题(本大题共12小题，每小题5分，共60分．每小题只有一个选项符合题意．）1.设复数，其中是实数，是虚数单位，若，则复数在复平面内对应的点位于（）A. 第一象限B. 第二象限C. 第三象限D. 第四象限【答案】A【解析】【分析】根据求出的值，得到，即可得到答案【详解】由可得：，解得，复数在复平面内对应的点位于第一象限故选【点睛】本题主要考查了复数的基本运算及其几何意义，首先求出的值，再判断对应点在复平面内所在的象限。

2020届云师大附中高三高考适应性月考（二）数学（理）试题一、单选题1．已知集合{}2230A x x x =-->，集合(){}lg 3B x y x ==+，则A B =I （）A ．{}31x x -<<- B ．{}3x x >C ．{}313x x x -<-或 D ．{}13x x -<<【答案】C【解析】根据一元二次不等式以及对数函数的定义域化简集合A 、B ，根据交集的定义写出A B I 即可. 【详解】2{|230}{|3A x x x x x =-->=>或1}x <-，{|lg(3)}{|3}B x y x x x ==+=>-，A B =I {|31x x -<<-或3}x >，故选C .【点睛】本题主要考查了集合的化简与运算问题，属于基础题． 2．设122iz i-+=+，则z 的虚部是（） A ．1 B ．iC ．-1D ．-i【答案】A【解析】根据复数的性质化简z ，结合虚部即可得到结果. 【详解】12i i(2i)i 2i 2iz -++===++，z 的虚部为1，故选A ． 【点睛】本题主要考查了复数的运算性质以及复数的分类，属于基础题.3．已知中心在原点，对称轴为坐标轴的双曲线的一条渐近线方程为y =，则该双曲线的离心率是（）A B C 2D 或2【答案】D【解析】分为焦点在x 轴上和焦点在y 轴上两种情形，由渐近线的方程得ba的值，结合2221b e a=+可得离心率的值.【详解】依题意，双曲线的焦点在x 轴上时，设它的方程为22221(00)x y a b ab-=>>，； 由渐近线方程为2y x =，得2b a=，故22213b e a =+=，即3e =，焦点在y 轴上时，设它的方程为22221(00)y xa b ab-=>>，， 由渐近线方程为2y x =，得2a b =，故222312b e a =+=，即62e =，故选D ． 【点睛】本题主要考查了双曲线的渐近线以及离心率的概念，掌握2221b e a=+是解题的关键，属于中档题.4．下图的程序框图的算法思路源于我国数学名著《九章算术》中的“中国剩余定理”．若正整数N 除以正整数m 后得余数r ，则记为()mod N r m =，如：()82mod3=，则执行该程序框图输出的n 等于（）A ．7B ．6C ．5D ．8【答案】A【解析】由已知中的程序语句可知：该程序的功能是利用循环结构计算并输出变量n 的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案． 【详解】根据给定的程序框图，可知：第一次执行循环体得3n =，15M =，此时150(mod 5)=，不满足第一个条件； 第二次执行循环体得5n =，20M =，此时200(mod 5)=，不满足第一个条件； 第三次执行循环体得7n =，27M =，此时272(mod 5)=且2726M =>，既满足第一个条件又满足第二个条件，退出循环，输出7，故选A ． 【点睛】本题考查了程序框图的应用问题，解题时应模拟程序框图的运行过程，以便得出正确的结论，是基础题．5．根据如下样本数据得到的回归直线方程ˆˆˆybx a =+，则下列判断正确的是（ ）A ．ˆˆˆ0,0.94b b a <+=B ．ˆˆˆ0,40.9b b a >+=C ．ˆˆˆ0,0.94a b a <+=D ．ˆˆˆ0,40.9a b a >+=【答案】D【解析】先根据增减性得ˆ0,b<再求,x y 代入验证选项． 【详解】因为随着x 增加，y 大体减少，所以ˆ0,b< 因为234564 2.50.50.524,0.955x y +++++-+-====，所以$0.94ba =+$，$0,a ∴> 故选D 【点睛】本题考查回归直线方程，考查基本分析判断能力，属基础题. 6．在ABC ∆中，D 在边AC 上满足12AD DC =u u u vu u u v ，E 为BD 的中点，则CE =uu u v（） A ．5163BA BC -u uu v u u u vB ．1536BA BC -u u u v u u u v C ．1536BA BC +u u u v u u u vD ．5163BA BC +u uu v u u u v【答案】B【解析】根据E 为中点，首先易得1122CE CB CD =+u u u r u u u r u u u r，再通过向量加法以及向量的减法和12AD DC =u u u r u u u r 即可得到结果.【详解】 如图所示：因为E 为BD 的中点，所以1122CE CB CD =+u u u r u u u r u u u r ，又12AD DC =u u u r u u u r ，23CD CA =u u u r u u u r ∴，12CE CB =u u u r u u u r ∴12111115()23232336CA CB CA CB BA BC BA BC +⨯=+=+-=-u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r，故选B ．【点睛】本题主要考查平面向量基本定理的应用，对向量加法和减法的运用较为灵活，属于基础题．7．已知实数x ，y 满足约束条件0301x y x y y -≥⎧⎪+-≤⎨⎪≥⎩，则22x y z -+=的最大值是（）A ．2B ．1C ．12D ．-1【答案】C【解析】由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，联立方程组求出最优解的坐标，代入目标函数得答案． 【详解】由实数x ，y 满足约束条件0301x y x y y -⎧⎪+-≤⎨⎪⎩……，作出可行域如图，则212x z -+=的最大值就是2t x y =-+的最大值时取得，联立01x y y -=⎧⎨=⎩,解得(1,1)A .化目标函数2t x y =-+为2y x t =+，由图可知，当直线2y x t =+过点A 时，直线在y 轴上的截距最大，此时z有最大值为12，故选C .【点睛】本题考查简单的线性规划，考查了数形结合的解题思想方法，是基础题．8．()26112x x x ⎛⎫+- ⎪⎝⎭的展开式中，含2x 的项的系数是（） A ．-40 B ．-25C ．25D ．55【答案】B【解析】写出二项式61x x ⎛⎫- ⎪⎝⎭的展开式中的通项，然后观察含2x 的项有两种构成，一种是()212x+中的1与61x x ⎛⎫- ⎪⎝⎭中的二次项相乘得到，一种是()212x +中的22x 与61x x ⎛⎫- ⎪⎝⎭中的常数项相乘得到，将系数相加即可得出结果。

2024-2025学年福建师大附中高一（上）月考数学试卷（10月份）一、单选题：本题共8小题，每小题5分，共40分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.已知集合A ={0,1}，B ={1,2}，则A ∪B 中元素的个数为( )A. 1B. 2C. 3D. 42.设集合M ={x|x 2−x ≥0}，N ={x|x <2}，则M ∩N =( )A. {x|x ≤0}B. {x|1≤x <2}C. {x|x ≤0或1≤x <2}D. {x|0≤x ≤1}3.函数f(x)= 3x −9的定义域为( )A. [−3,+∞) B. [−2,+∞) C. [2,+∞) D. [4,+∞)4.已知函数f(x)=ln x−ax 2+ax 恰有两个零点，则实数a 的取值范围为( )A. (−∞,0)B. (0,+∞)C. (0,1)∪(1,+∞)D. (−∞,0)∪{1}5.偶函数f(x)在区间[0,a](a >0)是单调函数，且满足f(0)⋅f(a)<0，则函数f(x)在区间[−a,a]内零点的个数是( )A. 1B. 2C. 3D. 46.已知函数f(x)={|log 3x|,x >0x 2+4x +1,x ≤0，函数F(x)=f(x)−b 有四个不同的零点x 1，x 2，x 3，x 4，且满足：x 1<x 2<x 3<x 4，则x 4x 3−x 1x 23+x 2x 232的取值范围是( )A. [2 2,+∞) B. (3,839] C. [3,+∞) D. [2 2,839]7.定义域R 的函数f(x)满足f(x +2)=3f(x)，当x ∈[0,2]时，f(x)=x 2−2x ，若x ∈[−4,−2]时,f(x)≥118(3t −t)恒成立，则实数t 的取值范围是( )A. (−∞,−1]∪(0，3]B. (−∞,− 3]∪(0, 3]C. [−1,0)∪[3，+∞)D. [− 3,0)∪[ 3,+∞)8.设函数f(x)的定义域为R ，且f(x)=13f(x +1)，当x ∈(−1,0]时，f(x)=x(x +1)，若对任意x ∈(−∞,m]，都有f(x)≥−8116，则实数m 的取值范围是( )A. (−∞,73]B. (−∞,114]C. (−∞,94]D. (−∞,3]二、多选题：本题共3小题，共18分。

江西师大附中高三年级数学（理）月考试卷命题人：蔡卫强 审题人：郑永盛 2017年10月第Ⅰ卷（选择题部分，共60分）一、选择题：共12小题，每小题5分，共60分.在每个小题给出的四个选项中，只有一项是符合题目要求的.1．已知集合{}12|>=xx A ,{}2log 0B x x =<，则A C B =（ ） A.()0,1B.(]0,1C. [)1,+∞D.()1,+∞ 2．若命题:p 对任意的x R ∈，都有3210x x -+<，则p ⌝为（ ）A. 不存在x R ∈，使得3210x x -+<B. 存在x R ∈，使得3210x x -+<C. 对任意的x R ∈，都有3210x x -+≥D. 存在x R ∈，使得3210x x -+≥ 3．已知角θ的终边经过点()(),30P x x <且cos 10x θ=，则x 等于（ ） A ．1-B ．13-C ．3-D．3-4. 为了得到函数sin 23y x π⎛⎫=- ⎪⎝⎭的图像，可以将函数cos 2y x =的图像（ ） A. 向左平移512π个单位 B. 向右平移512π个单位 C. 向右平移6π个单位 D. 向左平移6π个单位 5．已知()()()()1231ln 1a x ax f x xx -+<⎧⎪=⎨≥⎪⎩ 的值域为R ，那么a 的取值范围是( )A ．(－∞，－1]B ．(－1，12)C ．[－1，12)D ．(0，12)6. 已知函数()2tan 2(0,1)1xxa f xb x x a a a =++>≠+，若()12f =，则()1f -等于（ ）A. 3B. 3-C. 0D. 1-7．函数2ln x x y x=的图象大致是（ ）AB C D8．已知3tan 44πα⎛⎫+= ⎪⎝⎭，则2cos 4πα⎛⎫-= ⎪⎝⎭（ ） A.725B.925 C. 1625D.24259．已知偶函数2f x π⎛⎫+ ⎪⎝⎭，当,22x ππ⎛⎫∈- ⎪⎝⎭时， ()13sin f x x x =+． 设()1a f =，()2b f =， ()3c f =，则（ ）A. a b c <<B. b c a <<C. c b a <<D. c a b <<10.已知三角形ABC 内的一点D 满足2D A D B D B D C D C D A ===-，且|||||D A D B D C ==，平面ABC 内的动点P ，M 满足||1AP =，PM MC =，则2||BM 的最大值是（ ）A ．494B ．434C.D 11. 已知函数()2sin(2)(||)f x x ϕϕπ=-+<，若5(,)58ππ是()f x 的一个单调递增区间，则ϕ的取值范围是（ ） A. 93[,]1010ππ-- B. 29[,]510ππ C. [,]104ππD. [,](,)104ππππ--U12．已知函数()()()221ln ,,1xf x ax a x x a Rg x e x =-++∈=--，若对于任意的()120,,x x R ∈+∞∈，不等式()()12f x g x ≤恒成立，则实数a 的取值范围为（ ）A. [)1,0- B.[]1,0- C. 3,2⎡⎫-+∞⎪⎢⎣⎭D. 3,2⎛⎤-∞- ⎥⎝⎦第Ⅱ卷（非选择题部分，共90分）本卷包括必考题和选考题两个部分. 第13题～第21题为必考题，每个考生都必须作答. 第22题～第23题为选考题，考生根据要求作答.二、填空题：本大题共4小题，每小题5分,共20分.13．平行四边形ABCD 中，M 为BC 的中点，若AB AM DB λμ=+，则λμ-=______． 14．已知函数()sin 6f x x πω⎛⎫=+⎪⎝⎭，其中0ω>．若()12f x f π⎛⎫≤⎪⎝⎭对x R ∈恒成立，则ω的最小值为____．15．设锐角ABC 的三内角,,A B C 所对边的边长分别为,,a b c ，且1,2a B A ==，则b 的取值范围为 ． 16. 给出下列命题中①非零向量 a b 、满足a b a b ==-，则与a a b +的夹角为030； ② ⋅＞0是 a b 、的夹角为锐角的充要条件； ③若2,AB AB AC BA BC CA CB =⋅+⋅+⋅则ABC ∆必定是直角三角形；④△ABC 的外接圆的圆心为O ，半径为1，若2AB AC AO +=,且OA CA =，则向量BA 在向量BC 方向上的投影为32. 以上命题正确的是 （注：把你认为正确的命题的序号都填上）三、解答题：本大题共6小题，共70分. 解答应写出文字说明、证明过程或演算步骤． 17．（本小题满分12分）在△ABC 中，a ， b ，c 分别是角A ，B ，C 的对边，且2cos A cos C (1－tan A tan C )＝1． （1）求B 的大小；（2）若b ＝3，求△ABC 面积的最大值． 18．（本小题满分12分）已知函数f (x )＝2cos x cos ⎝⎛⎭⎫x －π6－3sin 2x ＋sin x cos x . (1)求f (x )的最小正周期；(2)若关于x 的方程()10f x a -+=在x ∈⎣⎡⎦⎤0，π2上有两个不同的实根，求实数a 的取值范围. 19．（本小题满分12分）如图所示的几何体是由棱台111ABC A B C -和棱锥11D AA C C -拼接而成的组合体，其底面四边形ABCD 是边长为2的菱形，且60BAD ∠=︒，1BB ⊥平面ABCD ，11122BB A B ==．（1）求证：平面1AB C ⊥平面1BB D ； （2）求二面角11A BD C --的余弦值． 20．（本小题满分12分）设离心率为 的椭圆2222:1x y E a b+= 的左、右焦点为12F F 、,点P 是E 上一点,12PF PF ⊥ , 12PF F ∆内切圆的半径为1 .(1)求E 的方程;(2)矩形ABCD 的两顶点C 、D 在直线2y x =+上，A 、B 在椭圆E 上,若矩形ABCD 的周长为 , 求直线AB 的方程.21．（本小题满分12分） 已知函数()22ln f x x x ax =--.（1）若曲线()y f x =在点()()1,1f 处的切线方程为30x y b ++=，求a ，b 的值； （2）如果()1212,x x x x <是函数()f x 的两个零点，()'f x 为函数()f x 的导数， 证明：122'03x x f +⎛⎫< ⎪⎝⎭请考生在第（22）、（23）两题中任选一题作答，如果多做，则按所做的第一题记分，作答时用2B 铅笔在答题卡上把所选题目的题号涂黑，把答案填在答题卡上． 22．（本题满分10分）选修4-4：坐标系与参数方程 在平面直角坐标系xoy 中，已知圆C 的参数方程为12cos 2sin x y θθ=+⎧⎨=⎩()θ为参数，直线l 的参数方程为523x ty t =-⎧⎨=-⎩()t 为参数，定点()1,1P .（1）以原点O 为极点，x 轴的非负半轴为极轴，单位长度与平面直角坐标系下的单位长度相同建立极坐标系，求圆C 的极坐标方程；（2）已知直线l 与圆C 相交于,A B 两点，求PA PB -的值.23．（本小题满分10分）选修4-5：不等式选讲 已知函数()1()0f x x a x a a=+++>.（1）当2a =时，求不等式()3f x >的解集； （2）求证：1()()4f m f m+-≥.江西师大附中高三年级数学（理）月考试卷命题人：蔡卫强 审题人：郑永盛 2017年10月第Ⅰ卷（选择题部分，共60分）一．选择题：共12小题，每小题5分，共60分.在每个小题给出的四个选项中，只有一项是符合题目要求的.1．已知集合{}12|>=xx A ,{}2log 0B x x =<，则A C B =（ ） A.()0,1B.(]0,1C. [)1,+∞D.()1,+∞ 【答案】C2．若命题:p 对任意的x R ∈，都有3210x x -+<，则p ⌝为（ ）A. 不存在x R ∈，使得3210x x -+<B. 存在x R ∈，使得3210x x -+<C. 对任意的x R ∈，都有3210x x -+≥D. 存在x R ∈，使得3210x x -+≥ 【答案】D3．已知角θ的终边经过点()(),30P x x <且cos x θ=，则x 等于（ ） A ．1- B ．13-C ．3-D．3-【答案】A4. 为了得到函数sin 23y x π⎛⎫=-⎪⎝⎭的图像，可以将函数cos 2y x =的图像（ ） A. 向左平移512π个单位 B. 向右平移512π个单位C. 向右平移6π个单位D. 向左平移6π个单位 【答案】B5．已知()()()()1231ln 1a x a x f x xx -+<⎧⎪=⎨≥⎪⎩ 的值域为R ，那么a 的取值范围是( )A ．(－∞，－1]B ．(－1，12)C ．[－1，12)D ．(0，12)【答案】C6. 已知函数()2tan 2(0,1)1xxa f xb x x a a a =++>≠+，若()12f =，则()1f -等于（ ）A. 3B. 3-C. 0D. 1-【答案】A7．函数2ln x xy x=的图象大致是（ ）AB C D【答案】D8．已知3tan 44πα⎛⎫+= ⎪⎝⎭，则2cos 4πα⎛⎫-= ⎪⎝⎭（ ） A.725B. 925C. 1625D.2425【答案】B9．已知偶函数2f x π⎛⎫+ ⎪⎝⎭，当,22x ππ⎛⎫∈- ⎪⎝⎭时， ()13sin f x x x =+． 设()1a f =，()2b f =， ()3c f =，则（ ）A. a b c <<B. b c a <<C. c b a <<D. c a b <<【答案】D10.已知三角形ABC 内的一点D 满足2D A D B D B D C D C D A ===-，且|||||D A D B D C ==，平面ABC 内的动点P ，M 满足||1AP =，PM MC =，则2||BM 的最大值是（ ） A ．494B ．434C. 3763+D 37233+ 【答案】A11. 已知函数()2sin(2)(||)f x x ϕϕπ=-+<，若5(,)58ππ是()f x 的一个单调递增区间，则ϕ 的取值范围是（ ） A. 93[,]1010ππ-- B. 29[,]510ππ C. [,]104ππD. [,](,)104ππππ--U【答案】C12．已知函数()()()221ln ,,1xf x ax a x x a Rg x e x =-++∈=--，若对于任意的()120,,x x R ∈+∞∈，不等式()()12f x g x ≤恒成立，，则实数a 的取值范围为（ ）A. [)1,0-B. []1,0-C. 3,2⎡⎫-+∞⎪⎢⎣⎭D. 3,2⎛⎤-∞-⎥⎝⎦【答案】B解：()()12f x g x ≤Q 恒成立 ∴只需()()1min f x g x ≤由()1xg x e x =--得：()'1xg x e =-，令()'0g x >解得：0x >()g x ∴在(),0-∞单调递减，在()0,+∞单调递增 ()()min 00g x g ∴==()10,x ∴∀∈+∞，()211121ln 0ax a x x -++≤恒成立 即只需()max 0f x ≤()()()()2'22112111221ax a x ax x f x ax a x x x-++--=--+== 当0a >时，令21a x a += 则21211ln ln 20a a f a a a ++⎛⎫⎛⎫⎛⎫==+> ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，与()0f x ≤矛盾当0a ≤时，210ax -< ()'0f x ∴>解得1x < ()f x ∴在()0,1单调递增，在()1,+∞单调递减()()()max 1211f x f a a a ∴==-+=-- 101a a ∴--≤⇒≥-综上所述：[]1,0a ∈-第Ⅱ卷（非选择题部分，共90分）本卷包括必考题和选考题两个部分. 第13题～第21题为必考题，每个考生都必须作答.第22题～第23题为选考题，考生根据要求作答.二．填空题：本大题共4小题，每小题5分,共20分.13．平行四边形ABCD 中，M 为BC 的中点，若AB AM DB λμ=+，则λμ-=__________．【答案】1314．已知函数()sin 6f x x πω⎛⎫=+⎪⎝⎭，其中0ω>．若()12f x f π⎛⎫≤⎪⎝⎭对x R ∈恒成立，则ω的最小值为____．【答案】415．设锐角ABC 的三内角,,A B C 所对边的边长分别为,,a b c ，且1,2a B A ==，则b 的取值范围为____．【答案】16. 给出下列命题中① 非零向量 a b 、满足a b a b ==-，则与a a b +的夹角为030； ② a ⋅b ＞0是 a b 、的夹角为锐角的充要条件； ③若2,AB AB AC BA BC CA CB =⋅+⋅+⋅则ABC ∆必定是直角三角形；④△ABC 的外接圆的圆心为O ，半径为1，若2AB AC AO +=,且OA CA =，则向量BA在向量BC 方向上的投影为32. 以上命题正确的是 （注：把你认为正确的命题的序号都填上） 【答案】①③④三．解答题：本大题共6小题，共70分. 解答应写出文字说明、证明过程或演算步骤． 17．（本小题满分12分）在△ABC 中，a ，b ，c 分别是角A ，B ，C 的对边，且2cos A cos C (1－tan A tan C )＝1． （1）求B 的大小；（2）若b ＝3，求△ABC 面积的最大值．解：（1）由2cos A cos C (1－tan A tan C )＝1， 得sin sin 2cos cos 11cos cos A C A C A C ⎛⎫-= ⎪⎝⎭．∴()2cos cos sin sin 1A C A C -=． ∴()1cos 2A C +=． ∴ 1cos 2B =-． 又 0B <<π, ∴23B π=． （2）222222cos 3,b a c ac B a c ac ac =+-=++≥又b ＝3， ∴ 3ac ≤． 1s i n 2ABC S ac B ∆∴=≤所以当且仅当a c ==ABC S有最大值为418．（本小题满分12分）已知函数f (x )＝2cos x cos ⎝⎛⎭⎫x －π6－3sin 2x ＋sin x cos x . (1)求f (x )的最小正周期；(2)若关于x 的方程()10f x a -+=在x ∈⎣⎡⎦⎤0，π2上有两个不同的实根，求实数a 的取值范围.解析：(1)f (x )＝2cos x cos(x －π6)－3sin 2x ＋sin x cos x ＝3cos 2x ＋sin x cos x －3sin 2x ＋sin x cos x ＝3cos2x ＋sin2x ＝2sin ⎝⎛⎭⎫2x ＋π3， ∴T ＝π. (2)()()101f x a a f x -+=⇔-=画出函数()f x 在x ∈⎣⎡⎦⎤0，π212a <-<或01a <-<故a 的取值范围为1)()31,3+.19．（本小题满分12分）如图所示的几何体是由棱台111ABC A B C -和棱锥11D AA C C -拼接而成的组合体，其底面四边形ABCD 是边长为2的菱形，且60BAD ∠=︒，1BB ⊥平面ABCD ，11122BB A B ==．（1）求证：平面1AB C ⊥平面1BB D ； （2）求二面角11A BD C --的余弦值． 解：（1）∵1BB ⊥平面ABCD ∴1BB ⊥AC在菱形ABCD 中，BD ⊥AC 又1BD BB B ⋂=∴AC ⊥平面1BB D ∵AC ⊂平面1AB C ∴平面1AB C ⊥平面1BB D（2）连接BD 、AC 交于点O ，以O 为坐标原点，以OA以OD 为y 轴，如图建立空间直角坐标系.1(0,1,0),(0,1,0),(0,1,2),B D B A --11111,2)22B A BA A =⇒-，同理11(2C -131(,2)2BA =,(0,2,0)BD =,11(,2BC =-设平面1A BD 的法向量),,(z y x n =∴100BA n BD n ⎧⋅=⎪⎨⋅=⎪⎩，则(n =- 设平面DCF 的法向量),,(z y x =10BD m BC m ⎧⋅=⎪⎨⋅=⎪⎩，则m = 设二面角11A BD C --为θ，13cos 19m n m nθ⋅==20．（本小题满分12分）设离心率为 2的椭圆2222:1x y E a b+= 的左、右焦点为12F F 、, 点P 是E 上一点,12PF PF ⊥ , 12PF F ∆内切圆的半径为 1 .(1)求E 的方程;(2)矩形ABCD 的两顶点C 、D 在直线2y x =+上，A 、B 在椭圆E 上,若矩形ABCD 的周长为, 求直线AB 的方程. 解：（1）直角三角形12PF F 内切圆的半径12121(||||||)2r PF PF F F a c =+-=- 依题意有1a c -=又2c a =，由此解得1a c ==，从而1b =故椭圆E 的方程为2212x y += （2）设直线AB 的方程为y x m =+，代入椭圆E 的方程，整理得2234220x mx m ++-=，由0∆>得m <<设1122(,),(,)A x y B x y ，则21212422,33m m x x x x -+=-=21|||AB x x =-=而||AC =m <<知||AC =所以由已知可得||||6AB AC +=，即36=， 整理得24130710m m +-=，解得1m =或()7141m =-增根，舍去 所以直线AB 的方程为1y x =+.21．（本小题满分12分） 已知函数()22ln f x x x ax =--.（1）若曲线()y f x =在点()()1,1f 处的切线方程为30x y b ++=，求a ，b 的值； （2）如果()1212,x x x x <是函数()f x 的两个零点，()'f x 为函数()f x 的导数， 证明：122'03x x f +⎛⎫<⎪⎝⎭解：（1）a =3,b =1 （2）()121212262'2323x x f x x a x x +⎛⎫=-+-⎪+⎝⎭ ()1212,x x x x <是函数()f x 的两个零点()()21111222222ln 02ln 0fx x x ax fx x x ax ⎧=--=⎪∴⇒⎨=--=⎪⎩()2121212lnx x a x x x x =-+- ()()212112211212212ln26261'232323x x x x f x x a x x x x x x x x +⎛⎫∴=-+-=--- ⎪++-⎝⎭()221103x x --< ∴只需证()2212112211212ln6602ln 022x x x x x x x x x x x x --<⇔-<+-+21221131ln 012x x x x x x ⎛⎫- ⎪⎝⎭⇔-<+ ，令()21,1,x t t x =∈+∞则设()()31ln 12t h t t t -=-+ 下面证()0h t < ()10,h =()()()()2141'21t t h t t t --=-+ ()1,'0t h t >∴<恒成立 ()h t ∴在()1,+∞单调递减，()()10h t h ∴<= 即122'03x x f +⎛⎫< ⎪⎝⎭请考生在第（22）、（23）两题中任选一题作答，如果多做，则按所做的第一题记分，作答时用2B 铅笔在答题卡上把所选题目的题号涂黑，把答案填在答题卡上．22．（本题满分10分）选修4-4：坐标系与参数方程在平面直角坐标系xoy 中，已知圆C 的参数方程为12cos 2sin x y θθ=+⎧⎨=⎩()θ为参数，直线l 的参数方程为523x t y t =-⎧⎨=-⎩()t 为参数，定点()1,1P . （1）以原点O 为极点，x 轴的非负半轴为极轴，单位长度与平面直角坐标系下的单位长度相同建立极坐标系，求圆C 的极坐标方程； （2）已知直线l 与圆C 相交于,A B 两点，求PA PB -的值.解：（1）依题意得圆C 的一般方程为()2214x y -+=，将cos ,sin x y ρθρθ==代入上式得22cos 30ρρθ--=，所以圆C 的极坐标方程为22cos 30ρρθ--=；（2）依题意得点()1,1P 在直线l 上，所以直线l 的参数方程又可以表示为121x t y t=-⎧⎨=-⎩()t 为参数，代入圆C 的一般方程为()2214x y -+=得25230t t --=， 设点,A B 分别对应的参数为12,t t ，则1212230,055t t t t +=>=-<， 所以12,t t 异号，不妨设120,0t t ><，所以2,PA PB ==，所以)125PA PB t t -=+=.23．（本小题满分10分）选修4-5：不等式选讲已知函数()1()0f x x a x a a=+++>. （1）当2a =时，求不等式()3f x >的解集；（2）求证：1()()4f m f m+-≥.解：（1）当a =2时，1()|2|||,2f x x x =+++原不等式等价于 112222111232323222x x x x x x x x x ⎧⎧<--≤≤->-⎧⎪⎪⎪⎪⎪⎨⎨⎨---->⎪⎪⎪+-->+++>⎩⎪⎪⎩⎩或或 解得11144x x <-∅>或或故不等式()3f x >的解集是111{|},(5)44x x x <->或分 （2）证明：11111(m)()||||||||f f m a m a m a m m a +-=++++-++-+ 1111||||||||m a a m m a m a =++-++++-+ 112|m |2(||)4||m m m ≥+=+≥ 当且仅当1,1m a =±=时等号成立。

2024-2025学年江西师大附中高三（上）第三次月考数学试卷一、单选题：本题共8小题，每小题5分，共40分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.复数z 满足|z−i|=2,z 在复平面内对应的点为(x,y)，则( )A. (x−1)2+y 2=4B. (x−1)2+y 2=2C. x 2+(y−1)2=4D. x 2+(y−1)2=22.如图，在△ABC 中，点D 在BC 的延长线上，|BD|=3|DC|，如果AD =x AB +y AC ，那么( )A. x =12,y =32B. x =−12,y =32C. x =−12,y =−32D. x =12,y =−323.纯洁的冰雪，激情的约会，2030年冬奥会预计在印度孟买举行.按常理，该次冬奥会共有7个大项，如冰球、冰壶、滑冰、滑雪、雪车等；一个大项又包含多个小项，如滑冰又分为花样滑冰、短道速滑、速度滑冰三个小项.若集合U 代表所有项目的集合，一个大项看作是几个小项组成的集合，其中集合A 为滑冰三个小项构成的集合，下列说法不正确的是( )A. “短道速滑”不属于集合A 相对于全集U 的补集B. “雪车”与“滑雪”交集为空集C. “速度滑冰”与“冰壶”交集不为空集D. 集合U 包含“滑冰”4.已知直线l ：x +y−3=0上的两点A ，B ，且|AB|=1，点P 为圆D ：x 2+y 2+2x−3=0上任一点，则△PAB 的面积的最大值为( )A.2+1B. 22+2C.2−1D. 22−25.已知函数f(x)的部分图象如图所示，则f(x)的解析式可能为( )A. f(x)=xcosπx B. f(x)=(x−1)sinπx C. f(x)=xcos[π(x +1)]D. f(x)=(x−1)cosπx6.已知正数a ，b ，c 满足2022a =2023，2023b =2022，c =ln2，下列说法正确的是( )A. log a c >log b cB. log c a >log c bC. a c <b cD. c a <c b7.已知抛物线C 1：y =x 2+2x 和C 2：y =−x 2+a ，若C 1和C 2有且仅有两条公切线l 1和l 2，l 1和C 1、C 2分别相切于M ，N 点，l 2与C 1、C 2分别相切于P ，Q 两点，则线段PQ 与MN ( )A. 总是互相垂直 B. 总是互相平分C. 总是互相垂直且平分D. 上述说法均不正确8.在平面四边形ABCD 中，AB ⊥AC ，且AB =AC ，AD = 2CD =22，则BD 的最大值为( )A. 27B. 6C. 25 D. 23二、多选题：本题共3小题，共18分。

第3章 函数的概念与性质压轴题专练一、单选题1．（2021·全国）已知定义在R 上的偶函数()f x 满足：当0x ≥时，()2x f x =，且(2)(3)f x af x +≤-对一切x ∈R 恒成立，则实数a 的取值范围为（ ） A ．1,32⎡⎫+∞⎪⎢⎣⎭B ．1,32⎛⎤-∞ ⎥⎝⎦C ．[32,)+∞D ．(0,32]2．（2021·奉新县第一中学高一月考）已知函数()()f x g x 、是定义在R 上的函数，其中()f x 是奇函数，()g x 是偶函数，且()()22f x g x ax x +=++，若对于任意1212x x <<<，都有()()12122g x g x x x ->--，则实数a 的取值范围是（ ）A ．1(,][0,)2-∞-⋃+∞ B ．(0,)+∞C ．1[,)2-+∞D ．1[,0)2-3．（2021·全国）设函数()f x 的定义域为R ，满足(2)2()f x f x -=，且当[)2,0x ∈-时，()2(2)f x x x =-+．若对任意[),x m ∈+∞，都有3()4f x ≤，则m 的取值范围是（ ） A ．2,3⎡⎫+∞⎪⎢⎣⎭B ．3,4⎡⎫+∞⎪⎢⎣⎭C ．1,2⎡⎫+∞⎪⎢⎣⎭D ．3,2⎡⎫+∞⎪⎢⎣⎭4．（2021·全国）函数()f x 是定义在R 上的偶函数，(1)f x -是奇函数，且当01x <≤时，()2020log f x x =，则1(2019)2020f f ⎛⎫+-= ⎪⎝⎭（ ）A ．1B ．1-C ．12020D ．20205．（2021·全国）设函数()f x m =,()a b a b <，使()f x 在[,]a b 上的值域为[,]a b ，则实数m 的取值范围是（ ） A ．9,24⎛⎤-- ⎥⎝⎦B ．52,4⎡--⎫⎪⎢⎣⎭C ．93,4⎡⎫--⎪⎢⎣⎭D ．95,44⎡⎤--⎢⎥⎣⎦6．（2021·全国）关于函数()1x f x x =-，给出以下四个命题：（1）当0x >时，()y f x =单调递减且没有最值； （2）方程()(0)f x kx b k =+≠一定有实数解；（3）如果方程()f x m =（m 为常数）有解，则解的个数一定是偶数； （4）()y f x =是偶函数且有最小值．其中正确的命题个数为（ ） A ．1B ．2C ．3D ．4二、多选题7．（2020·重庆市第七中学校）定义在R 上的奇函数()f x 和偶函数()g x 满足：()()4x f x g x +=，则下列结论正确的有（ ）A ．44()2x xf x --=，且()g x 在R 上单调递增 B ．x R ∀∈，总有22[()][()]1g x f x -=；C ．x R ∀∈，总有()()()()0f x g x f x g x --+=D ．0x R ∃∈，使得()()()00022f x f x g x >8．（2021·全国）（多选题）已知函数()f x 的定义域为D ，若存在区间[,]m n D ⊆使得()f x ： （1）()f x 在[,]m n 上是单调函数； （2）()f x 在[,]m n 上的值域是[2,2]m n ， 则称区间[,]m n 为函数()f x 的“倍值区间”． 下列函数中存在“倍值区间”的有（ ） A ．2()f x x =；B ．1()f x x=； C ．1()f x x x=+；D ．23()1xf x x =+． 9．（2021·全国）1837年，德国数学家狄利克雷(P.G.Dirichlet ，1805-1859)第一个引入了现代函数概念：“如果对于x 的每一个值，y 总有一个完全确定的值与之对应，那么y 是x 的函数”.由此引发了数学家们对函数性质的研究.下面是以他的名字命名的“狄利克雷函数”：1,()0,R x QD x x Q∈⎧=⎨∈⎩(Q 表示有理数集合)，关于此函数，下列说法正确的是（ ） A ．()D x 是偶函数 B ．,(())1x R D D x ∀∈=C ．对于任意的有理数t ，都有()()D x t D x +=D ．存在三个点112233(,()),(,()),(,())A x D x B x D x C x D x ，使ABC 为正三角形10．（2020·福建）设()f x 是定义在R 上的函数，若存在两个不相等的实数12,x x ，使得()()121222f x f x x x f ++⎛⎫= ⎪⎝⎭，则称函数()f x 具有性质P ，那么下列函数中，具有性质P 的函数有（ ） A ．()1,00,0x f a x x ⎧≠⎪=⎨⎪=⎩B ．()21f x x =-C ．()2log f x x =D ．()2x f x e =-11．（2021·湖南高一期末）设x ∈R ，用[]x 表示不超过x 的最大整数，则[]y x =称为高斯函数，也叫取整函数.令()[]f x x x =-，以下结论正确的有（ ） A ．()1.10.9f -= B ．函数()f x 为奇函数 C ．()()11f x f x +=+D ．函数()f x 的值域为[)0,112．（2021·杭州市富阳区第二中学高一月考）已知定义在R 上的函数()f x 的图象连续不断，若存在常数()t t R ∈，使得()()0f x t tf x ++=对任意的实数x 成立，则称()f x 是回旋函数.给出下列四个命题中，正确的命题是（ ） A ．常值函数()(0)f x a a =≠为回旋函数的充要条件是1t =-； B ．若(01)x y a a =<<为回旋函数，则1t >； C ．函数2()f x x =不是回旋函数；D ．若()f x 是2t =的回旋函数，则()f x 在[0]4030，上至少有2015个零点. 13．（2020·沙坪坝·重庆南开中学高一月考）一般地，若函数()f x 的定义域为[],a b ，值域为[],ka kb ，则称为的“k 倍跟随区间”；若函数的定义域为[],a b ，值域也为[],a b ，则称[],a b 为()f x 的“跟随区间”.下列结论正确的是（ ）A ．若[]1,b 为()222f x x x =-+的跟随区间，则2b =B ．函数()11f x x=+存在跟随区间C ．若函数()f x m =1,04m ⎛⎤∈- ⎥⎝⎦D ．二次函数()212f x x x =-+存在“3倍跟随区间”三、双空题14．（2021·北京朝阳·高一期末）已知函数()221x x mf x +=+.①当0m =时，()f x 的值域为______；②若对于任意,,a b c ∈R ，()f a ，f b ，()f c 的值总可作为某一个三角形的三边长，则实数m 的取值范围是______. 15．（2021·江苏扬中市第二高级中学）已知函数()12sin 221xf x x =-+，则函数()()1g x f x =+是___________函数(从“奇”，“偶”，“非奇非偶”及“既是奇函数又是偶函数”中选择一个填空)，不等式2()(410)2f x x f x -+-≤-的解集为___________. 四、填空题16．（2020·河南郑州一中高一月考）函数()40ay x a x=+>在[]1,2上的最小值为8，则实数a =______. 17．（2020·华东师范大学松江实验高级中学高一月考）定义区间（,a b ），（,a b ]，[],a b 的长度均为d b a =-，多个区间并集的长度为各区间长度之和，例如（1，2）[3，5）的长度()()21533d =-+-=，设()[]{}(),1f x x x g x x =⋅=-，其中[x ]表示不超过x 的最大整数，例如[1.3]=1，[-1.4]=-2；[3]=3，{x }=x -[x ].若用d 表示不等式()()f x g x ≥解集区间的长度，则当x ∈[-2021，2021]时，d =___________；18．（2021·江苏南京师大附中）已知函数()222131x x f x x =-++．若存在()1,4m ∈使得不等式()()2432f ma f m m -++>成立，则实数a 的取值范围是________．19．（2020·四川乐山·高一期末）已知函数1(2)21,2()2,2x a x a x f x a x --++⎧=⎨>⎩（0a >且1a ≠），若() f x 有最小值，则实数a 的取值范围为_______________________.20．（2021·上海）已知a R ∈，函数()22,011,02x a x x f x x ax a x ⎧++-≥⎪=⎨-++<⎪⎩的最小值为2a ，则由满足条件的a 的值组成的集合是_______________.21．（2021·全国）下列命题中所有正确的序号是__________. ①函数1()3x f x a -=+(1a >)在R 上是增函数；②函数(1)f x -的定义域是(1,3)，则函数()f x 的定义域为(2,4)； ③已知53()8f x x ax bx =++-，且(2)8f -=，则(2)8f =-； ④11()122x f x =--为奇函数.⑤函数()f x =[]0,422．（2019·福建师大二附中高一期中）关于函数()()2lg 4lg ||f x x x =+-，下列命题中所有正确结论的序号是______.①其图象关于y 轴对称；②当0x >时，是增函数；当0x <时，是减函数； ③()f x 的最小值是2lg 2；④()f x 在区间1,0、2,上是增函数；五、解答题23．（2021·浙江高一单元测试）已知函数()()2f x x x a =+，2()1x a g x x +=+，[]2,2a ∈-. （1）当1a =-时，求函数()f x 的单调递增区间；（2）若[]11,1x ∀∈-，∃唯一的[]20,2x ∈，使得()()12f x g x =，求实数a 的取值范围.24．（2021·全国）已知函数2()21x x m nf x ⋅+=+，且1m n >+.（1）判断()f x 在定义域上的单调性，并用定义证明；（2）若0m n +=，且2(4)(4)0f x f a x ++->恒成立，求a 的范围.25．（2021·黑龙江哈尔滨市第六中学校）已知函数()21x f x ax b +=+是定义域上的奇函数，且()12f -=-.（1）求函数()f x 的解析式，判断函数()f x 在()0,∞+上的单调性并证明；（2）令()()ln h x f x x a =-+⎡⎤⎣⎦，设0a >，若对任意1,14b ⎡⎤∈⎢⎥⎣⎦，当[]12,,1x x b b ∈+时，都有()()12ln 4h x h x -≤，求实数a 的取值范围.26．（2020·安徽省怀宁中学）已知()f x 是定义在R 上的奇函数，且3()()2f x af x x =--（a 为常数），且(1)1f =． （1）求()f x 的解析式；（2）若存在0x >，使得不等式()53()26f x x m x x x +≥-+成立，求m 的取值范围．27．（2020·宝山区·上海交大附中）已知函数()2mf x x x=++（m 为常数）（1）若函数()y f x =图象上动点P 到定点Q （0，2m 的值；（2）设0m <，若不等式()f x kx ≤在1,12x ⎡⎤∈⎢⎥⎣⎦有解，求k 的取值范围；（3）定义：区间[,]a b （a b <）的长度为b a -，若4m =，问是否存在区间[,]a b ，使得()f x 的值域为[6，7]，若存在，求出此区间长度的最大值与最小值的差.28．（2021·宝山·上海交大附中高一期中）设是()y f x =定义在D 上的函数，若对任何实数()0,1α∈以及D 中的任意两数1x 、2x ，恒有()()()()()121211f x x f x f x αααα+-≤+-，则称()f x 为定义域上的C 函数． （1）判断函数1y x=，(),0x ∈-∞是否为定义域上的C 函数，请说明理由； （2）函数3y x =，(),x M ∈+∞是定义域上的C 函数，求实数M 的最小值；（3）若()y f x =是定义域为R 的周期函数，且最小正周期为T ．试判断()y f x =是否可能为定义域上的C 函数．如果可能，请给出至少一个符合条件的函数()y f x =；如果不可能，请说明理由．29．（2021·浙江高一期末）设函数2()2(2)||f x x x a x a =+--． （1）若1a =，求函数()f x 的值域； （2）求函数()f x 在区间[1,1]-的最小值．30．（2021·江西高安中学高一月考）已知函数()131.3x x f x b+-+=+（1）当1b =时，求满足()3xf x =的x 值；（2）当3b =时，①存在t R ∈，不等式()()2222f t t f t k -<-有解，求k 的取值范围；②若函数()g x 满足()()()12333x xf xg x -⋅+=-⎡⎤⎣⎦，若对任意x ∈R ，不等式()()211g x m g x +≥恒成立，求实数m 的最大值；。