小学生毕业总复习专项练习题库(操作、图形)

2013～2014学年度第二学期六年级数学下册总复习分项练习卷—操作部分1、按要求在下面方格中作图并完成填空。

（1）画出图形①中轴对称图形的另一半。

（2）量一量：图②三角形ABC 中，顶点A 在顶点C 的（ ）偏（ ）（ ）°方向。

（3）画出图②中三角形ABC 绕顶点C 按顺时针方向旋转90°后的图形。

（4）画出图③中梯形按2:1放大后的图形，放大后的梯形的面积是（ ）cm ²。

（5）画出图④向右平移4格后的图形。

2、按要求作图。

（1）画出从上面观察图1所看到的图形。

（2）分别画出下面图形绕A 点顺时针方向旋转90°后的图形及向右平移4格后的图形。

3、量一量、算一算、画一画。

（1） 体育馆与校门之间的图上距离是（ ）厘米。

经考察：体育馆与校门之间的实际距离为75米，这幅图的比例尺是（ ）。

（2） 校园内有一个圆形花坛，花坛的圆心在校门北偏东500方向距校门50米处，花坛半径上面图1 A10 为25米，请在图上画出这个圆形花坛。

4．按要求画一画。

5．按要求画一画。

6．按要求填一填、画一画。

（1格代表1cm ²）（1）画出图①中长方形绕A 点逆时针方向旋转90°后的图形；旋转后，C 点的位置用数对表示是（ ， ）。

（2）画出图②中三角形按3:1放大后的图形，放大后的三角形的面积是（ ）㎝²。

（3）请在方格纸空白处设计一个面积为12㎝²的轴对称图形，并画出1条对称轴。

体育馆9 1113 123 4 5 6 7 8 10 12 14 0 15 16 17 18 19 2037412 5689（1）过A 点分别画出直线b的垂线和平行线。

（2）在方格中画出从左面观察下图所看到的图形。

bA C ①② （1）在下图中表示出少年宫的位置：少年宫在学校西偏北25°方向900m 处。

（2）以学校所在点为圆心，画一个半径450m 的圆。

小学六年级毕业班数学总复习专项训练（图形与位置、图形的变换）（满分100，时间90分钟）一、“认真细致”填一填。

（每空1分，共31分）1.在平面图上通常确定的方位是：上北、下（ ）、左（ ）、右（ ）。

2.小明现在的位置可以用（9，8）表示，他向正北方向走5格，再向正东方向走3格到达少年宫，少年宫的位置是（ ， ）。

3.一个四边形周长是22厘米，面积是34平方厘米。

如果将这个四边形按3：1的比放大后，新图形的周长是（ ）厘米，面积是（ ）平方厘米。

4.一个直角三角板的两条直角边分别为a 、b ，以a 为轴旋转一周，在你眼前出现一个（ ），a 是它的（ ），b 是它的（ ）。

5.线段比例尺表示地图上1厘米的距离相当于实际距离（ ）千米。

改写成数字比例尺是（ ）。

6.小明下午放学回家，面向太阳走，他的前面是（ ），后面是（ ），左面是（ ）。

7.（1）王老师家的位置是（ ， ）丁丁家的位置是（ ， ），红红家的位置是（ ， ）。

（2）以王老师家为中心，丁丁家在[（ ）偏（ ）]（ ）的方向上；红红家在[（ ）偏（ ）]（ ）的方向上。

8.下面的现象中是平移的画“△”，是旋转的画“□”。

①推拉门的移动。

（ ） ②拉动抽屉。

（ ） ③钟面上的分针。

（ ）④飞机的螺旋桨的运动。

（ ） ⑤工作中的电风扇的风叶。

（ ）9.观察图形，填空。

找出下面图形的变化规律，然后在最后一个图的空格里画上相关的图形。

0 50 100 150 200千米 王老师家红红家丁丁家54 3 2 10 1 2 3 4 5 6 7 8 9 10 11北10.把一个长、宽分别为10厘米、8厘米的长方形，拉成一个一条高为9厘米的平等四边形，拉成的平行四边形的面积是（ ）平方厘米。

11.君君看电影时买的票是C 排16座，如果用数对表示是（16，C ），和他同时在这个放映厅看电影的球球的位置是（8，F ），这表示球球坐在这个放映厅的（ ）排（ ）座。

小学六年级数学学科毕业专项训练复习资料
数学操作题练习
动动巧手，操作计算。

1、下图是一个长方形(单位：厘米)，这个长方形的周长为24厘米，长和宽的比是2：1，那么长为( )厘米，宽为( )厘米。

(1)请你以A 点为圆心，以AB 为半径画一个圆， 这个圆与长方形组合成新的图形。

(2)求这个组合成的新图形的面积。

2、有一块长20米，宽10米的长方形地，请你有用
500
1
的比例尺把它画出来。

（1）、在长方形内，画一个最大的半圆，并标出该图的对称轴。

（2）、现在要以每隔2厘米的距离，在半圆的边上栽树，大约能栽多少棵？
3、如右图，已知长方形ABCD 的面积是88平方厘米， E 和F 分别是长和宽的中点。

（1）画出长方形ABCD 的所有对称轴。

（2）求出阴影部分的面积。

4、下面是一个半圆，请画出它的对称轴。

量出它 的半径，并计算它的周长和面积。

（量取整厘米数）
5、在下面的方格中先画一个平行四边形，再画一个和它面积相等的梯形。

6、在一块长50米，宽20米的长方形草地中央，拴着一匹马。

（1）、这匹马的缰绳至少长几米？（2分）
（2）、请你自己选择一定的比例尺，画出示意图，并用阴影标出马吃草的最大范围。

（4分）
（3）、请你计算马吃草的最大面积（2分）
7、下图中的拆线表示送水管，小明家（A点）和小芳家（B点）分别在送水管的两侧。

现在要从送水管上分别接一根引水管到家。

请你想一想，怎样接最省料，在图中画出管线，量一量管线的长度（取整厘米），算一算各家至少需要准备多少米长的水管？。

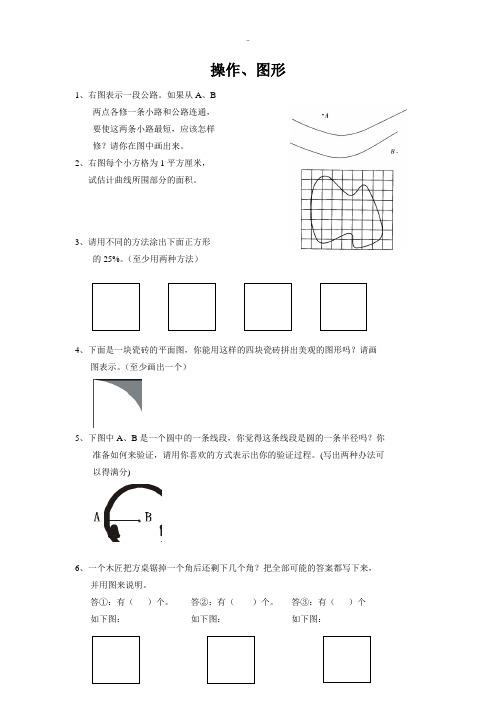
操作、图形1、右图表示一段公路。

如果从A 、B两点各修一条小路和公路连通， 要使这两条小路最短，应该怎样 修？请你在图中画出来。

2、右图每个小方格为1平方厘米， 试估计曲线所围部分的面积。

3、请用不同的方法涂出下面正方形的25%。

（至少用两种方法）4、下面是一块瓷砖的平面图，你能用这样的四块瓷砖拼出美观的图形吗？请画图表示。

（至少画出一个）5、下图中A 、B 是一个圆中的一条线段，你觉得这条线段是圆的一条半径吗？你准备如何来验证，请用你喜欢的方式表示出你的验证过程。

(写出两种办法可 以得满分)6并用图来说明。

答①：有（ ）个。

答②：有（ ）个。

答③：有（ ）个 如下图： 如下图： 如下图：7、哪两种物体经过组合可得到长方体、正方体、圆锥？请连线。

（6分）8、图形与计算。

图形介绍：这是一把打开的扇子。

我们想计算它的周长如图2，你能计算圆 的周长，那么，你能计算这把扇子的周长吗？9、操作计算。

（1）根据右图完成下列各题。

①把线段比例尺改成数值比例尺是（ ）。

②量得AC 的长是（ ）厘米，AC 的实际长度是（ ）米。

③量得∠B=（ ）度。

（精确到十位） ④画出从B 点到AC 边的最短路线。

⑤求出△ABC 的图上面积是（ ）平方厘米。

（2）自学下面这段材料，然后回答问题。

我们知道，在整数中“两个数的和等于这两个数的积”的情形并不多，例如2+2=2×2。

但是在分数中，这种现象却很普遍。

请观察下面的几个例子：因为：74 +73 =4112 ,74 ×73 =4112 ,所以74 +73 =74 ×73 。

因为：95 +94 =4120 ,95 ×94 =4120 ,所以95 +94 =95 ×94。

根据以上结果，我们发现了这样的一个规律：两个分数，如果它们的（ ）相同，并且（ ），那么这两个分数的和等于它们的积。

例如（ ）+（）=（）×（）。

1、按要求画图形。

（规定每个小正方形的边长都是1厘米）B①A（1）把图①按2∶1的比放大，放大后的图形A点的对应位置是（2，8）。

（2）把图①绕B点逆时针旋转90度，再把旋转后的图形向东平移8厘米。

（3）在B点北偏东450方向画一个半径2厘米的圆。

2、红星小学的操场长100米，宽60米。

请你先选取一个合适的比例尺（打“√”），再画出这个操场的平面图，并在上面标上相应的图上距离。

①1︰1000（）②1000︰1 （）③1︰2000 （）④2000︰1（）比例尺：3、算一算，填一填，画一画。

（1）书店在区政府（）方向（）米处。

（2）图书馆在区政府（）偏（）方向（）米处。

（3）学校在区政府北偏西60°方向600米处，请列式计算并在图上标出。

4、先测量本张试卷的长和宽（保留整厘米数），再从下面的比选取一个，画出试卷扩大或缩小后的示意图，请在示意图中注明选用比与有关数据。

（①2︰1 ②1︰2 ③1︰10 ④1︰20）5.按1:3的比画出长方形缩小后的图形，按2:1的比画出直角三角形放大后的图形。

6.⑴管委会位于中心花园( )面大约( )米处⑵运河小学在中心花园北偏东60°方向500米处，请用“·”在图中画出实验小学的位置⑶在图中先量一量好又多超市到中心花园的图上距离，再算一算好又多超市到中心花园的实际距离。

7、画一画，想一想。

5%（1）旋转前A点的位置，用数对表示是（，）。

（2）把图中的圆向右平移5格，与原来的圆组成轴对称图形，画出他的所有对称轴。

（3）按1∶2的比画出三角形缩小后的图形。

三角形缩小后的面积是原来的（）。

N管委会中心花园●0 200 400 600米好又多超市8、找一找，标一标。

1、以金沙广场为观测点，市政府在金沙广场的（ ）方向（ ）米处。

2、城南公园在金沙广场南偏西20°方向的800米处，请在图中表示出城南公园的位置。

9. 小方家在学校北偏西300方向400米处， 小丽家在学校正南方向300米处，请在右图 中分别标出小方家、小方家的位置。

第1页 共4页 第2页 共4页AB C六年级数学下册专项归类复习题（操作题专项练习）1、一个小正方形，它的边长增加8厘米后，面积就增加了224平方厘米。

（1）要求先画出示意图，并用阴影标出增加了的面积。

（3分） （2）求小正方形的边长多少厘米。

（提示用方程解）（5分）2、如左图，已知长方形ABCD 的面积是88平方厘米，E 和F 分别是长和宽的中点。

（1）画出长方形ABCD 的所有对称轴。

（画虚线）（2分） （2）求出阴影部分的面积。

（4分）3、有一块长120米，宽80米的长方形空地，请你按一定的比例，画出空地的平面图，然后在平面图上用阴影标出41的草坪。

（注意：要标明你所采用的比例尺及相应的长和宽）（5分）。

4、圆的面积与长方形的面积相等，已知圆的周长62.8厘米，求阴影部分的周长。

（6分）5、一个圆柱底面直径是10厘米，高是20厘米，把圆柱的侧面沿着它的一条高剪开，再打开，然后按1：10的比例尺画出它的侧面展开图。

并标明数据。

（6分）6、画一个周长是12.56厘米的圆，用字母o 、r 分别标出它的圆心和半径，并求出这个圆的面积。

（5）7、三角形ABC 的面积是36平方厘米，求阴影部分的面积。

（单位：厘米）（5分）8、求图形中阴影部分的面积。

（单位：厘米）（6分）9、梯形面积为60平方厘米，上底是下底的2倍，已知梯形的高5厘米，求阴影部分的面积。

（6）※※※※※※※答※※※※题※※※※不※※※※超※※※※过※※※※此※※※※线※※※※※※※§§§§§§§§§§§密§§§§§§§§§§§§封§§§§§§§§§§线§§§§§§§§§牟定县实验小学 五年级 班 姓名 考号FABCD EO r12222共4页 第3页 共4页 第4页O10、计算下面的阴影部分的面积。

操作、图形1、右图表示一段公路。

如果从A、B两点各修一条小路和公路连通，要使这两条小路最短，应该怎样修？请你在图中画出来。

2、右图每个小方格为1平方厘米，试估计曲线所围局部的面积。

3、请用不同的方法涂出下面正方形的25%。

〔至少用两种方法〕4、下面是一块瓷砖的平面图，你能用这样的四块瓷砖拼出美观的图形吗？请画图表示。

〔至少画出一个〕5、以下图中A、B是一个圆中的一条线段，你觉得这条线段是圆的一条半径吗？你准备如何来验证，请用你喜欢的方式表示出你的验证过程。

(写出两种方法可以得总分值)6、一个木匠把方桌锯掉一个角后还剩下几个角？把全部可能的答案都写下来，并用图来说明。

答①：有〔〕个。

答②：有〔〕个。

答③：有〔〕个如以下图：如以下图：如以下图：17、哪两种物体经过组合可得到长方体、正方体、圆锥？请连线。

〔 6分〕8、图形与计算。

图形介绍：这是一把翻开的扇子。

我们想计算它的周长如图 2，你能计算圆的周长，那么，你能计算这把扇子的周长吗？9、操作计算。

1〕根据右图完成以下各题。

①把线段比例尺改成数值比例尺是〔〕。

②量得AC 的长是〔〕厘米，AC 的实际长度是〔〕米。

③量得∠B=〔〕度。

〔精确到十位〕 ④画出从B 点到AC 边的最短路线。

⑤求出△ABC 的图上面积是〔 〕平方厘米。

〔2〕自学下面这段材料，然后答复以下问题。

我们知道，在整数中“两个数的和等于这两个数的积〞的情形并不多，例如 2+2=2×2。

但是在分数中，这种现象却很普遍。

请观察下面的几个例子： 因为： 7+ 7 =4 1 , 7 × 7 1 ,所以 7 7 7743124=4 12+ = ×。

34 3 4 39 9 1 9 9 1 9 9 9 9因为： 5+4 =4 20,5 × 4=4 20,所以 5 +4 =5 ×4。

根据以上结果，我们发现了这样的一个规律：两个分数，如果它们的〔 〕相同，并且〔 〕，那么这两个分数的和等于它们的积。

组合图形1、求下列组合图形阴影部分的面积。

2、①求它的周长和面积。

（单位：厘米）②圆的周长是18.84cm，求阴影部分面积。

③长方形的面积和圆的面积相等，已知圆④求直角三角形中阴影部分的面积。

的半径是3cm，求阴影部分的周长和面积。

（单位：分米）
⑤下图中长方形长6cm，宽4cm，已知阴影⑥图中阴影①比阴影②面积小48平方厘米，
①比阴影②面积少3cm2，求EC的长。

AB=40cm，求BC的长。

⑦平行四边形的面积是30cm2，⑧一个圆的半径是4cm，求阴影部分面积。

求阴影部分的面积。

⑨已知AB=8cm，AD=12cm，三角形ABE和三角形ADF的面积，各占长方形ABCD的1/3，求
三角形AEF的面积。

⑩梯形上底8cm，下底16cm，阴影⑾求阴影部分面积。

（单位：cm）部分面积64cm2，求梯形面积。

⑿梯形面积是48平方厘米，阴影部分比空白⒀阴影部分比空白部分大6cm2，求S 阴。

部分12平方厘米，求阴影部分面积。

3、求下列图形的体积。

（单位：厘米）。

高山中心小学小升初质量监测图形与几何专项练习
（操作与实践一）
班级：姓名：成绩：
一. 按要求在方格纸上画图，并回答问题。

（每个小方格的对角线表示200米）（1）广场的位置用数对表示是（）。

（2）以L为对称轴，画出①号图的另一半，使它成为一个轴对称图形。

（3）画出②号图向下平移3格后的图形。

（4）画出③号图绕点O按逆时针方向旋转90°后的图形。

（5）从广场先向西走5格，再向北走2格是少年宫，请在图中标出少年宫的位置。

（6）李先生从汽车站去
广场，要从南偏东45°
方向走600米，请在图上
标出汽车站的位置。

（7）在方格图中画出④
号图从左侧观察到的形
状
二，操作与实践。

1.下图中每个小方格的边长表示1厘米。

（1）用数对表示梯形中A点的位置:
（）；画出这个梯形绕A点顺时针
旋转90°后的图形。

（2）将图中的圆按2:1放大，画出放大后
的圆，要求与原来的圆组成一个圆环；这
个圆环的面积是（）平方厘米。

（可
以用含有π的式子表示）。

小学六年级数学毕业复习图形操作练习题1．画一个半径是1厘米的半圆，并标出它的圆心．半径和直径。

2．画出下面各图形底边上的高。

3．把下面的图形按要求分割（1）在三角形中添一条线段，把它分一分，看看谁的分法多。

（2）把五边形按要求进行分割4、AB是一条街道，要从点P修一条小路通向街道AB，怎么修最省工省料？（用线段在图上画出这条线路）如果这幅图的比例尺是1：20000，这条小路实际是多少米？（测量时取整厘米）5、从下面长方形纸上剪下一部分，要折成一个棱长3厘米的正方形，可以怎么剪？设计两种不同的方案，在图中涂色表示6、（1）画一个边长4厘米的正方形。

（2）在正方形中画一个最大的圆。

（3）如果在正方形中把这个圆剪掉，剩下部分的面积是多少？（4）余下的部分有（ ）条对称轴。

7、(1)画出图①的另一半，使它成为一个轴对称图形。

再将画好的完整图形先向右平移8格，再向下平移1格。

(2)图中圆的圆心的位置用数对表示是（），O点的位置可用数对表示是（）。

将圆按3：1的比放大，并以O点为圆心画出放大后的圆。

原来圆的面积和放大后圆面积的比是（）。

(3)请将图②绕A点顺时针旋转90。

，画出旋转后的图形。

8、画一个底是3厘米，一个底角是50°的等腰三角形。

9、画出下列图形底边上的高。

10、下图是（）角，（）°，以角的两边为相邻边画一个平行四边形，并画出一条高。

11、已知三角形的面积是24平方厘米，画出这个三角形。

12、一个长方形草坪,长50米,宽30米，用12000的比例尺画出这块草坪的平面图。

13、请用不同的方法涂出下面正方形的25%。

（至少用两种方法）14、量出下面左图中半圆的半径长度(取整厘米数) 半径长( )厘米。

并列式计算出它的周长和面积。

15、在下面方格中画出两个和阴影三角形面积相等，形状不相同的三角形。

16、在平行四边形中完成下面的操作。

（1）过A点画BC边上的高。

（2）量出BC边的长是（）厘米。