凸轮轮廓曲线的设计

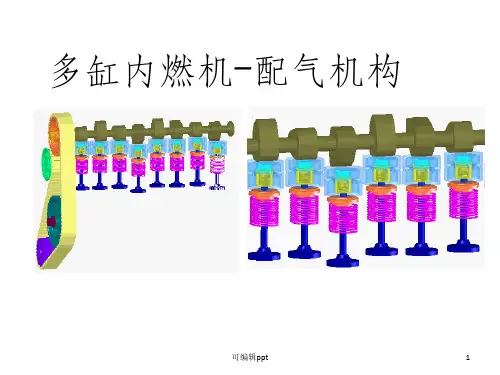
第三节 盘形凸轮廓线的设计当根据工作要求和结构条件选定了凸轮机构的类型、从动件的运动规律和凸轮的基圆半径（其确定将在下节中介绍）等结构参数后，就可以设计凸轮的轮廓曲线。

凸轮廓线的设计方法有图解法和解析法，其设计原理基本相同。

本节先简要介绍图解法，后重点介绍解析法设计凸轮廓线。

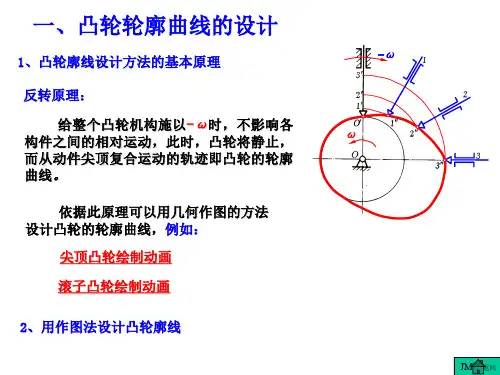
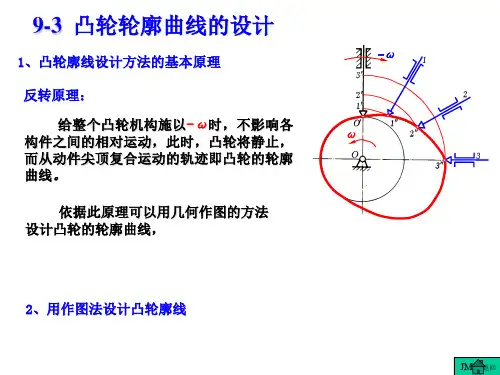
一、凸轮廓线设计的基本原理图4-13 反转法设计凸轮廓线基本原理图4-13所示为一尖顶对心盘形凸轮机构，设凸轮以等角速度ω逆时针转动，推动从动件2在导路中上、下往复移动。

当从动件处于最低位置时，凸轮轮廓曲线与从动件在A 点接触，当凸轮转过1ϕ角时，凸轮的向径A A 0将转到A A '0位置，而凸轮轮廓将转到图中虚线所示的位置。

从动件尖端从最低位置A 上升至B '，上升的位移为B A S '=1，这是从动件的运动位移。

若设凸轮不动，从动件及其运动的导路一起绕A 0点以等角速度-ω转过1ϕ角，从动件将随导路一起以角速度-ω转动，同时又在导路中作相对导路的移动，如图中的虚线位置，此时从动件向上移动的位移为B A 1。

而且，11S B A B A ='=，即在上述两种情况下，从动件移动的距离不变。

由于从动件尖端在运动过程中始终与凸轮轮廓曲线保持接触，所以从动件尖端的运动轨迹即为凸轮轮廓。

设计凸轮廓线时，可由从动件运动位移先定出一系列的B 点，将其连接成光滑曲线，即为凸轮廓线。

由于这种方法是假设凸轮固定不动而使从动件连同导路一起反转，故称为反转法。

对其它类型的凸轮机构，也可利用反转法进行分析和凸轮廓线设计。

二、图解法设计凸轮廓线1. 移动从动件盘形凸轮廓线的设计（1）尖端从动件 图4-14a 所示为一偏置移动尖端从动件盘形凸轮机构。

设已知凸轮的基圆半径为b r ，从动件导路偏于凸轮轴心A 0的左侧，偏距为e ，凸轮以等角速度ω顺时针方向转动。

从动件的位移曲线如图4-14b 所示，试设计凸轮的轮廓曲线。

图4-14 尖端从动件盘形凸轮廓线设计依据反转法原理，具体设计步骤如下。

凸轮轮廓曲线设计的基本原理一、引言凸轮作为机械传动中的一种重要元件，其设计对于机械传动的性能具有重要影响。

凸轮轮廓曲线设计是凸轮设计中的一个关键环节，其目的是使得凸轮在运动过程中能够满足特定的运动要求。

本文将介绍凸轮轮廓曲线设计的基本原理。

二、凸轮运动学基础在介绍凸轮轮廓曲线设计之前，我们需要先了解一些凸轮运动学基础知识。

1. 凸轮类型根据不同的应用场景和工作要求，凸轮可以分为以下三种类型：（1）往复式凸轮：用于转换旋转运动为往复直线运动。

（2）回转式凸轮：用于转换旋转运动为旋转或者往复曲线运动。

（3）摆线式凸轮：用于将旋转运动转换为直线往复运动。

2. 凸轮参数在进行凸轮设计时，需要确定一些关键参数，包括：（1）基圆半径：即未加工前的圆形母体半径。

（2）偏心距：即摇杆中心线与凸轮中心线的距离。

（3）凸轮高度：即凸轮曲线顶点到基圆半径的距离。

（4）凸轮半径：即凸轮曲线顶点到凸轮中心线的距离。

3. 凸轮运动在运动学分析中，我们通常将凸轮视为一个旋转体，其运动可以分为两个方向：径向和周向。

根据不同的工作要求，我们可以通过调整凸轮参数来实现不同的运动方式。

三、凸轮轮廓曲线设计基本原理在进行凸轮设计时，我们需要根据具体的工作要求来确定其运动方式，并且通过合理的曲线设计来实现这种运动方式。

下面将介绍一些常用的凸轮曲线设计方法。

1. 圆弧法圆弧法是一种简单直观的凸轮曲线设计方法。

该方法将整个曲线分为多段圆弧，并且通过调整圆弧半径和连接处角度来控制曲线形状。

该方法适用于一些简单的往复或者回转式凸轮设计。

2. 三角函数法三角函数法是一种常用的摆线式凸轮设计方法。

该方法将凸轮曲线表示为三角函数的形式，通过调整函数参数来控制曲线形状。

该方法适用于一些要求高精度和高速度的摆线式凸轮设计。

3. 贝塞尔曲线法贝塞尔曲线法是一种基于数学模型的凸轮曲线设计方法。

该方法通过定义一些控制点，并且通过调整这些控制点来实现凸轮曲线的设计。

凸轮轮廓曲线的设计1. 引言凸轮是一种机械传动装置，常用于将圆周运动转换为直线或曲线运动。

凸轮的轮廓曲线设计是指根据特定要求和功能，确定凸轮的形状和尺寸的过程。

本文将详细介绍凸轮轮廓曲线的设计原理、方法和注意事项。

2. 凸轮轮廓曲线的基本原理凸轮的基本原理是通过其特定形状的外边缘，使其在旋转时能够驱动其他机械部件做直线或曲线运动。

凸轮的外形通常由一条或多条连续光滑的曲线构成，这些曲线被称为凸轮的轮廓曲线。

3. 凸轮轮廓曲线设计方法3.1 几何法几何法是最常用的凸轮轮廓曲线设计方法之一。

其基本步骤如下：1.确定所需运动类型：直线运动、往复运动、旋转运动等。

2.根据所需运动类型选择合适的基本函数：例如直线函数、正弦函数等。

3.根据基本函数的特点和要求，确定凸轮的参数：例如振幅、周期等。

4.利用基本函数和凸轮参数，绘制凸轮的轮廓曲线。

5.对绘制得到的曲线进行优化和调整，以满足设计要求。

3.2 数值法数值法是利用计算机辅助设计软件进行凸轮轮廓曲线设计的方法。

其基本步骤如下：1.确定凸轮的运动类型和要求。

2.利用计算机辅助设计软件创建凸轮模型。

3.在软件中选择合适的曲线函数和参数，并进行凸轮参数设置。

4.根据所选曲线函数和参数，生成凸轮的轮廓曲线。

5.对生成的曲线进行优化和调整，以满足设计要求。

3.3 实验法实验法是通过制作实物模型来进行凸轮轮廓曲线设计的方法。

其基本步骤如下：1.根据设计要求和实际情况，选择合适的材料和加工工艺制作凸轮模型。

2.在模型上标记出所需运动类型对应的参考点。

3.利用传感器等设备记录参考点在运动过程中的位置。

4.根据记录的数据，绘制凸轮的轮廓曲线。

5.对绘制得到的曲线进行优化和调整，以满足设计要求。

4. 凸轮轮廓曲线设计的注意事项在进行凸轮轮廓曲线设计时，需要注意以下几点：•凸轮的形状和尺寸应符合机械传动要求和设计规范。

•轮廓曲线应光滑、连续，避免出现尖锐转角和突变点。

•曲线参数的选择应合理，以确保凸轮能够正常运动并满足设计要求。

二、用图解法设计凸轮轮廓曲线 下面以偏置尖顶直动从动件盘形凸轮机构为例，讲解凸轮廓线的设计过程。

例6-1 对心直动尖顶从动件盘形凸轮机构设已确定基圆半径mm 150=r ，凸轮顺时针方向匀速转动，从动件行程mm 18=h 。

从动件运动规律如下表所示：推程 远休止 回程 近休止运动角1120δ=260δ=903=δ490δ=从动件运动规律等速运动正弦加速度运动设计步骤：1、建立推程段的位移方程：18120s δ=，回程段的位移方程：12π181sin 902π90s δδ⎡⎤⎛⎫=-+ ⎪⎢⎥⎝⎭⎣⎦，将推程运动角、回程运动角按某一分度值等分成若干份，并求得对应点的位移。

2、画基圆和从动件的导路位置3、画反转过程中从动件的各导路位置4、画从动件尖顶在复合运动中的各个位置点5、分别将推程段和回程段尖顶的各位置点连成光滑曲线，再画出远休止段和近休止段的圆弧，即完成了尖顶从动件盘形凸轮轮廓曲线的设计，如图6-18。

需要注意：同一个图上作图比例尺必须一致。

如各分点的位移与基圆应按相同比例尺量取。

2．偏置直动尖顶从动件盘形凸轮机构凸轮转动中心O 到从动件导路的垂直距离e 称为偏距。

以O 为圆心，e 为半径所作的圆称为偏距圆。

显然，从动件导路与偏距圆相切（图中K 为从动件初始位置与基圆的切点）。

在反转过程中，从动件导路必是偏距圆的切线。

如图6-19。

r0a A0A1OB0B1内 容3．直动滚子从动件盘形凸轮机构例题：已知：r r －滚子半径，0r －基圆半径，从动件运动规律。

设计该机构。

设计思路：把滚子中心看作尖顶从动件的尖顶，按前述方法先画出滚子中心所在的廓线——凸轮的理论廓线。

再以理论廓线上各点为圆心，以滚子半径r r 为半径画一系列的圆，这些圆的内包络线 即为凸轮的实际廓线（或称为工作廓线）。

如图6-16 注意：滚子从动件盘形凸轮的基圆半径是指其理论廓线的最小向径4．对心直动平底从动件盘形凸轮机构思路：把平底与导路的交点Ａ看作尖顶从动件的尖点，依次作出交点的位置，通过这些位置点画出从动件平底的各个位置线，然后作这些平底的包络线，即为凸轮的工作廓线，如图6-17图6-16图6-17图6-18图6-19内 容5．摆动尖顶从动件盘形凸轮机构已知：基圆半径0r ，摆动从动件的杆长为L （从尖点到从动件回转中心的距离），凸轮回转中心到从动件回转中心的距离a 。

基于matlab的凸轮轮廓曲线设计凸轮是机械中常见的关键零件之一，其主要功能是将旋转的运动转化为直线运动，用于推动某些机械元件进行工作。

凸轮轮廓曲线的设计对于凸轮的运动和工作效率有着重要的影响。

在本文中，我们将介绍基于matlab的凸轮轮廓曲线设计方法，以帮助读者了解凸轮轮廓曲线设计的基本概念和方法。

凸轮的形状通常是复杂的非圆形曲线。

凸轮的轮廓曲线设计过程中，需要考虑控制凸轮输送运动的速度和加速度等因素，同时还需要考虑各种机械元件之间的协调性和协定性。

针对以上问题，我们提出了基于连续逼近法的凸轮轮廓曲线设计方法。

1. 连续逼近法的基本原理连续逼近法是一种典型的非线性规划方法，其基本思想是将目标函数逐渐逼近最优解。

在凸轮轮廓曲线设计中，我们可以将凸轮轮廓曲线视为目标函数，通过不断调整曲线的形状，逐渐逼近最优轮廓曲线。

连续逼近法的具体实现过程包括以下步骤：（1）确定初始值首先需要确定一个初始轮廓曲线，通常可以使用圆弧、抛物线等基本曲线来作为起始轮廓曲线。

（2）建立数学模型接着需要建立凸轮轮廓曲线的数学模型，以便于通过数值方法来求解最优轮廓曲线。

其中，常见的模型包括三次贝塞尔曲线、三次样条曲线等。

（3）计算目标函数根据建立的数学模型，通过计算目标函数来评估轮廓曲线的性能。

通常，目标函数包括运动速度、加速度、平衡性等因素。

（4）优化轮廓曲线通过对目标函数的优化，不断调整轮廓曲线的形状，逐渐逼近最优曲线。

（5）确定最优解最终确定最优解，并验证其性能。

matlab是一种常见的数学软件，可以运用其强大的计算能力来进行凸轮轮廓曲线的设计。

具体实现过程如下：（1）数据处理将凸轮相关的数据通过matlab进行存储和处理。

常见的数据包括凸轮的尺寸、旋转角度、轮廓曲线等。

根据凸轮的数据建立轮廓曲线的数学模型，其中包括选择适当的曲线类型、确定曲线参数等。

（5）性能验证3. 总结。

§4—4 用解析法设计凸轮的轮廓曲线一、滚子从动件盘形凸轮1．理论轮廓曲线方程（1）直动从动件盘形凸轮机构图示偏置直动滚子从动件盘形凸轮机构。

求凸轮理论廓线的方程，反转法给整个机构一个绕凸轮轴心O 的公共角速度-ω，这时凸轮将固定不动，而从动件将沿-ω方向转过角度ϕ，滚子中心将位于B 点。

B 点的坐标，亦即理论廓线的方程为：⎭⎬⎫++=-+=ϕϕϕϕsin )(cos sin cos )(00s s e y e s s x （4-15） 220e r s a -=，r a 为理论廓线的基圆半径，对于对心从动件凸轮机构，因e=0，所以s 0=r a ⎭⎬⎫+=+=ϕϕs i n )(c o s )(s r y s r x a a （4-16） （2）摆动从动件盘形凸轮机构图所示为摆动滚子从动件盘形凸轮机构。

仍用反转法使凸轮固定不动，而从动件沿-ω方向转过角度ϕ，滚子中心将位于B 点。

B 点的坐标，亦即理论廓线的方程为：⎭⎬⎫-+-=-+-=)sin(sin )cos(cos 00ϕψψϕϕψψϕl a y l a x （4-17） ψ0为从动件的起始位置与轴心连线OA 0之间的夹角。

alr r l a T 2)(arccos 20220+-+=ψ （4-18） 在设计凸轮廓线时，通常e 、r 0、r T 、a 、l 等是已知的尺寸，而s 和ψ是ϕ的函数，它们分别由已选定的位移方程s =s (ϕ)和角位移方程ψ=ψ（ϕ）确定。

2．实际廓线方程滚子从动件盘形凸轮的实际廓线是圆心在理论廓线上的一族滚子圆的包络线。

由微分几何可知，包络线的方程为：⎪⎭⎪⎬⎫=∂∂=0),,(0),,(1111ϕϕϕy x f y x f （4-20） 式中x 1、y 1为凸轮实际廓线上点的直角坐标。

对于滚子从动件凸轮，由于产生包络线（即实际廓线）的曲线族是一族滚子圆，其圆心在理论廓线上，圆心的坐标由式（4-15）~（4-17）确定，所以由（4-20）有：0)()(),,(2212111=--+-=T r y y x x y x f ϕ0)(2)(2),,(1111=----=∂∂ϕϕϕϕd dy y y d dx x x y x f式（a ）和（b ）联立求解x 1和y 1，即得滚子从动件盘形凸轮的实际廓线参数方程： ⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛±=221221//ϕϕϕϕϕϕd dy d dx d dx r y y d dy d dx d dy r x x T T （4-21） 上面的一组加减号表示一根外包络廓线，下面的一组加减号表示另一根内包络廓线。