凸轮轮廓曲线设计

凸轮机构的类型虽然有多种，但绘制凸轮轮廓的基本原理及方法是相同的，凸轮轮廓都按反转法原理绘出。下面以常见的盘形凸轮为例，说明凸轮轮廓曲线的绘制方法。
凸轮转角
0°～180°
180°～300°
300°～360°
从动件的运动规律
等速上升30 mm
等加速等减速下降回到原处
停止不动
试设计此凸轮轮廓曲线。
解:设计步骤如下:1．按一定比例尺 =0.002 m/mm绘制从动件的位移线图（见下图(a)）。
对心直尖顶从动件盘形凸轮轮廓的设计
二、凸轮机构基本尺寸的确定
1.凸轮机构的压力角
2.基园半径的确定教学方法：利用动画演示作图法设计凸轮轮廓曲线的方法和步骤
课程作业或思考题：1、用反转法设计盘形凸轮的廓线时，应注意哪些问题？移动从动件盘形凸轮机构和摆动从动件盘形凸轮机构的设计方法各有什么特点？
参考资料或常用网址：韩玉成.机械设计基础.北京.电子工业出版社；庄宿涛.成都.西南交通大学出版社；徐刚涛.北京.高等教育出版社；http//
教具：多媒体
基本教材：陈立德《机械设计基础》（第四版）
课时安排：4
教学目的（分掌握、熟悉、了解三个层次）：1.了解凸轮轮廓“反转法原理”的设计方法；2.熟悉作图法设计凸轮轮廓曲线的方法；3.掌握凸轮机构基本尺寸的确定。
教学重点、难点#
重点：作图法设计凸轮轮廓曲线
难点：作图法设计凸轮轮廓曲线
凸轮轮廓的设计原理按从动件的已知运动规律绘制凸轮轮廓的基本原理是反转法。根据相对运动原理，若将上图所示的整个凸轮机构（凸轮、从动件、机架）加上一个与凸轮角速度大小相等、方向相反的公共角速度（ ），此时各构件之间的相对运动关系不变。这样，凸轮静止不动，而从动件一方面随机架和导路一起以等角速度“ ”绕凸轮转动，另一方面又按已知运动规律在导路中作往复移动（或摆动）。由于从动件的尖顶始终与凸轮轮廓保持接触，所以反转后从动件尖顶的运动轨迹就是凸轮轮廓。

第三节 盘形凸轮廓线的设计当根据工作要求和结构条件选定了凸轮机构的类型、从动件的运动规律和凸轮的基圆半径（其确定将在下节中介绍）等结构参数后，就可以设计凸轮的轮廓曲线。

凸轮廓线的设计方法有图解法和解析法，其设计原理基本相同。

本节先简要介绍图解法，后重点介绍解析法设计凸轮廓线。

一、凸轮廓线设计的基本原理图4-13 反转法设计凸轮廓线基本原理图4-13所示为一尖顶对心盘形凸轮机构，设凸轮以等角速度ω逆时针转动，推动从动件2在导路中上、下往复移动。

当从动件处于最低位置时，凸轮轮廓曲线与从动件在A 点接触，当凸轮转过1ϕ角时，凸轮的向径A A 0将转到A A '0位置，而凸轮轮廓将转到图中虚线所示的位置。

从动件尖端从最低位置A 上升至B '，上升的位移为B A S '=1，这是从动件的运动位移。

若设凸轮不动，从动件及其运动的导路一起绕A 0点以等角速度-ω转过1ϕ角，从动件将随导路一起以角速度-ω转动，同时又在导路中作相对导路的移动，如图中的虚线位置，此时从动件向上移动的位移为B A 1。

而且，11S B A B A ='=，即在上述两种情况下，从动件移动的距离不变。

由于从动件尖端在运动过程中始终与凸轮轮廓曲线保持接触，所以从动件尖端的运动轨迹即为凸轮轮廓。

设计凸轮廓线时，可由从动件运动位移先定出一系列的B 点，将其连接成光滑曲线，即为凸轮廓线。

由于这种方法是假设凸轮固定不动而使从动件连同导路一起反转，故称为反转法。

对其它类型的凸轮机构，也可利用反转法进行分析和凸轮廓线设计。

二、图解法设计凸轮廓线1. 移动从动件盘形凸轮廓线的设计（1）尖端从动件 图4-14a 所示为一偏置移动尖端从动件盘形凸轮机构。

设已知凸轮的基圆半径为b r ，从动件导路偏于凸轮轴心A 0的左侧，偏距为e ，凸轮以等角速度ω顺时针方向转动。

从动件的位移曲线如图4-14b 所示，试设计凸轮的轮廓曲线。

图4-14 尖端从动件盘形凸轮廓线设计依据反转法原理，具体设计步骤如下。

凸轮轴上凸轮轮廓的形状凸轮轴是内燃机中的重要零部件，其主要功能是控制气门的开闭时间和程度，以实现燃气进出气缸的控制。

凸轮轴上凸轮轮廓的形状对发动机的性能和效率有着重要影响。

凸轮的形状设计既要满足气门的开闭要求，又要考虑到发动机的整体性能。

常见的凸轮轮廓形状有椭圆形、正弦形、指数形和平顶形等。

椭圆形凸轮轮廓是一种常见的设计形式。

椭圆形凸轮轮廓的特点是在气门开启和关闭过程中，凸轮的升程和角度变化较为平缓，相对稳定。

这种形状的凸轮轮廓适用于普通发动机，能够平稳控制气门的开闭，提供较为均匀的气门升程和气门持续时间。

正弦形凸轮轮廓是一种较为复杂的设计形式。

正弦形凸轮轮廓的特点是在气门开启和关闭过程中，凸轮的升程和角度变化呈正弦曲线。

这种形状的凸轮轮廓可以实现更加精确的气门控制，提供更高的发动机性能。

但由于制造难度较大，成本较高，一般只用于高性能发动机或特殊应用。

指数形凸轮轮廓是一种较为特殊的设计形式。

指数形凸轮轮廓的特点是在气门开启和关闭过程中，凸轮的升程和角度变化呈指数曲线。

这种形状的凸轮轮廓可以实现更加精确的气门控制，提供更高的发动机性能。

指数形凸轮轮廓一般用于高性能发动机或特殊应用，能够提供更长的气门开启时间和更大的气门升程，以提高发动机的输出功率和扭矩。

平顶形凸轮轮廓是一种相对简单的设计形式。

平顶形凸轮轮廓的特点是在气门开启和关闭过程中，凸轮的升程和角度变化较为平缓，相对稳定。

这种形状的凸轮轮廓适用于普通发动机，能够平稳控制气门的开闭，提供较为均匀的气门升程和气门持续时间。

除了上述几种常见的凸轮轮廓形状，还有一些特殊的设计形式，如双凸轮轮廓、多凸轮轮廓等。

这些特殊的设计形式可以实现更加复杂和精确的气门控制，提供更高的发动机性能和效率。

凸轮轴上凸轮轮廓的形状选择应根据发动机的具体应用和设计要求来确定。

不同形状的凸轮轮廓对发动机的性能和效率有着不同的影响。

因此，在设计发动机时，应根据具体要求选择合适的凸轮轮廓形状，以实现最佳的发动机性能和效率。

授课教案No任务3.1 凸轮机构的认识一、复习10分钟复习上次课学习内容二、教师导课与课程学习：（1）学习提示，教师介绍本任务的学习内容。

15分钟本项目以直动从动件的盘形凸轮机构为例，在从动件等速运动、等加速等减速运动、余弦加速度运动（简谐运动）规律条件下，分析了凸轮机构中存在的柔性冲击与刚性冲击。

教师介绍本任务的学习内容：凸轮机构的分类；常用术语；从动件的运动规律；凸轮机构的结构形式；常用材料及热处理（2）分小组学习: 40分钟3.1.1常用设备中的凸轮机构1. 凸轮机构的组成如图所示的凸轮机构是由凸轮、从动件和机架等三个基本构件组成的机构。

2.凸轮机构应用实例自动钻床进给机构、冲床凸轮机构等。

3.1.2凸轮机构的分类凸轮机构的类型很多，按凸轮和从动件的形状及其运动形式的不同，凸轮机构的分类方法有以下几种：1.按凸轮形状分类(1）盘形凸轮（2）移动凸轮。

（3）圆柱凸轮2.按从动件形式分类（1）尖顶从动件（2）滚子从动件（3）平底从动件从动件的结构形式3.按从动件的运动形式分类学生发言汇报、记录学习笔记学生发言汇报并记录学习笔记阅读教材和PPT、分组讨论、撰写发言提纲、学生发言汇报，课，记录学习笔记No（1）直动从动件直动从动件指相对于机架作直线往复移动的从动件，如图3.1.1中所示。

直动从动件又分为对心直动从动件和偏置直动从动件。

（2）摆动从动件：绕某一固定转动中心摆动的从动件。

4.按凸轮与从动件的锁合方式分类 （1）力锁合利用从动件的重力、弹簧力或其他外力使从动件与凸轮轮廓保持接触，（2）形锁合利用从动件和凸轮特殊的几何形状来维持接触，例如圆柱凸轮机构是利用滚子与凸轮凹槽两侧面的配合来实现形锁合。

3.1.3凸轮机构的常用术语如下：1.凸轮基圆与基圆半径b r2.凸轮的转角δ凸轮相对于某一位置转过的角度，称为凸轮转角δ。

具体包括推程运动角0δ、远停程运动角S δ回程运动角0′δ和近停程运动角Sδ'。

反转法反转法根据相对运动原理321?一反转法的原理反转法根据相对运动原理若给整个凸轮机构附加一个运动机构的相对运动不变
第四章 凸轮机构
图解法设计对心尖顶直动
从动件盘形凸轮轮廓
主讲：陈艳巧
第四章 凸轮机构
图解法设计凸轮轮廓
设计问题 按给定的从动件运动规律设计凸轮轮廓曲线。 设计方法
解析法：精确，高效，可直接用于数控加工 编程，适用于高速和高精度凸轮。
剩余角度时，从动件不动。
(1)试绘制出从动件的位移曲线。 (2)已知凸轮基圆半径rb=40mm, 凸轮顺时针回转，设计一对心 直动尖顶从动件盘形凸轮 .
第四章 凸轮机构
Class is over！
5．量取相应位移
6．作轮廓线
10 9 8 7 4 11 0 1 2 3 6 5
s
h
h

ω1
0
1 2 3 4 5 6 7 8 9 10 11 12
1800 2100 3000 3600
第四章 凸轮机构
思考与练习
一凸轮机构从动件的运动规律为：从动件按等速运动规 律上升30mm，对应凸轮转角δ0=180°；从动件以等加、等减 速运动规律返回原处，对应凸轮转角δ0’=120°；当凸轮转过
6 7 8
第四章 凸轮机构 二、对心尖顶直动从动件盘形凸轮轮廓设计
解:1．作位移曲线 2．等份s- 图 3．作基圆 4． 沿- 等份基圆
已知：rb、h、ω1、从动件运动规律
凸轮转角 从动件运动
0 180
等速上升 h
180 210 远休止 210 300 等速下降 300 360 近休止
图解法：直观，简单；但误差大，效率低，适 于不重要的凸轮。
第四章 凸轮机构 一、反转法的原理

s
30
30
120
120
90
δ
360
七、解析法设计凸轮轮廓曲线
1、偏置直动滚子从动件盘形凸轮轮廓的设计
建立凸轮转轴中心的坐标系xOy
根据反转法原理，凸轮以w转过j角；
B点坐标为
x y
(s0 (s0
s) sin j s) cosj
e cosj esinj
上式即为凸轮理论廓线方程
实际廓线与理论廓线在法线上相距
凸轮机构由凸轮、从动件和机架三部分组成。
凸轮机构是高副机构，易于磨损，因此只适用于传 递动力不大的场合。
示例一 内燃机配气机构
示例二 靠模车削机构
示例 绕线机的凸轮绕线机构
示例 缝纫机的凸轮拉线机构
凸轮机构的主要优点： 使从动件实现预定的运动规律，结接触，容易磨损。 用于传递动力不大的控制机构或调节机构。
2、自D0起，沿-ω方向取δ1-4 角，等分各部分，从D1起以 从动件长度为半径作圆，与基 圆交于C点。
3、C1D1起，分别量取β角， 与2的圆交于B点，连接B0、 B1、B2…，即为凸轮曲线。
例题：设计盘形凸轮机构，已知凸轮角速度ω1逆时针转动， 基圆半径r0=30mm，从动件的行程h=40mm。从动件的 位移线图如下：
第四章 凸轮机构及间歇运动机构
§4-1 凸轮机构的应用和分类 §4-2 从动件常用的运动规律 §4-3 盘形凸轮轮廓曲线的设计 §4-4 凸轮机构设计中应注意的问题 §4-5 间歇运动机构
§4-1 凸轮机构的应用和分类
凸轮是一种具有曲线轮廓或凹槽的构件，它通过与从 动件的高副接触，在运动时可以使从动件获得连续或不 连续的任意预期运动。
当凸轮继续以角速度ω1逆时针 转过角度δ2时，从动件尖顶从 C到D，在最远位置停止不动， 对应的δ2是远休止角。

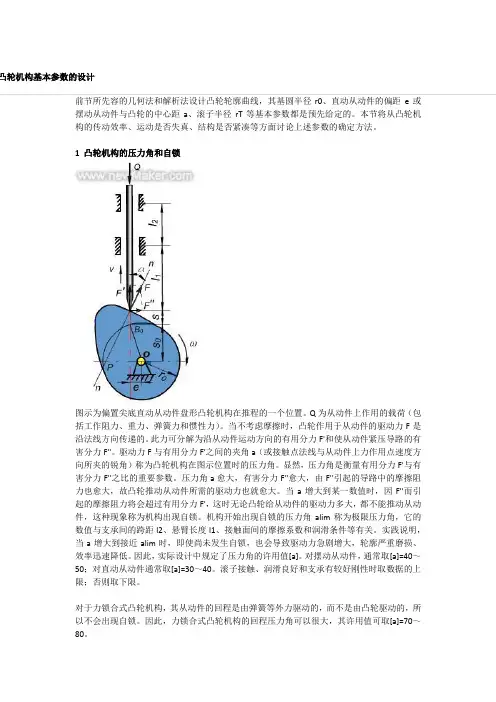
凸轮机构基本参数的设计前节所先容的几何法和解析法设计凸轮轮廓曲线，其基圆半径r0、直动从动件的偏距e或摆动从动件与凸轮的中心距a、滚子半径rT等基本参数都是预先给定的。

本节将从凸轮机构的传动效率、运动是否失真、结构是否紧凑等方面讨论上述参数的确定方法。

1 凸轮机构的压力角和自锁图示为偏置尖底直动从动件盘形凸轮机构在推程的一个位置。

Q为从动件上作用的载荷（包括工作阻力、重力、弹簧力和惯性力）。

当不考虑摩擦时，凸轮作用于从动件的驱动力F是沿法线方向传递的。

此力可分解为沿从动件运动方向的有用分力F'和使从动件紧压导路的有害分力F''。

驱动力F与有用分力F'之间的夹角a（或接触点法线与从动件上力作用点速度方向所夹的锐角）称为凸轮机构在图示位置时的压力角。

显然，压力角是衡量有用分力F'与有害分力F''之比的重要参数。

压力角a愈大，有害分力F''愈大，由F''引起的导路中的摩擦阻力也愈大，故凸轮推动从动件所需的驱动力也就愈大。

当a增大到某一数值时，因F''而引起的摩擦阻力将会超过有用分力F'，这时无论凸轮给从动件的驱动力多大，都不能推动从动件，这种现象称为机构出现自锁。

机构开始出现自锁的压力角alim称为极限压力角，它的数值与支承间的跨距l2、悬臂长度l1、接触面间的摩擦系数和润滑条件等有关。

实践说明，当a增大到接近alim时，即使尚未发生自锁，也会导致驱动力急剧增大，轮廓严重磨损、效率迅速降低。

因此，实际设计中规定了压力角的许用值[a]。

对摆动从动件，通常取[a]=40～50；对直动从动件通常取[a]=30～40。

滚子接触、润滑良好和支承有较好刚性时取数据的上限；否则取下限。

对于力锁合式凸轮机构，其从动件的回程是由弹簧等外力驱动的，而不是由凸轮驱动的，所以不会出现自锁。

因此，力锁合式凸轮机构的回程压力角可以很大，其许用值可取[a]=70～80。

图4.1 内燃机配气凸轮机构
图4.2
绕线机排线凸轮机构
图4.3所示为录音机卷带装置中的凸轮机构。工作时，凸 轮1处于图示最低位置，在弹簧5的作用下，安装于带轮轴上 的摩擦轮3紧靠卷带轮4，从而将磁带卷紧。停止放音时，凸 轮1随按键上移，其轮廓迫使从动件顺时针方向摆动，使摩 擦轮与卷带轮分离，从而停止卷带。
1. 多项式运动规律
多项式运动规律的一般形式为
s = C 0 + C 1δ + C 2 δ 2 + C 3δ 3 + L + C n δ n
式中， δ 为凸轮转角；s为从动件位 为凸轮转角；s C C C C C 移； 0 ， 1 ， 2 ， 3 ，…， n 为待定常数，可利用边 界条件来确定。 常用的有一次(n=1)多项式(即等速运动规律) 常用的有一次(n=1)多项式(即等速运动规律)；二次 (n=2)多项式(即等加速等减速运动规律)；五次(n=5) (n=2)多项式(即等加速等减速运动规律)；五次(n=5) 多项式运动规律。
图4.10 改进等速 运动规律
图4.11 改进等加速等减速 运动规律
【例4.1】 直动从动件凸轮机构。已知：从动件行程 h=20mm，推程运动角 δ t = 150° ，远休止角 δ s = 60°，回程 运动角 δ h = 120° ，近休止角 δ 's = 30° ；从动件推程、回程分 别采用简谐运动规律和摆线运动规律。试写出从动件一 个运动循环的位移、速度和加速度方程。 解：(1) 从动件推程运动方程。 推程段采用简谐运动规律，故将推程运动角 δ t = 150° 5π /6、行程h=20mm代入简谐运动规律推程运 = 动方程式，可推出
● 4.4 凸轮轮廓曲线的设计——解析法 凸轮轮廓曲线的设计——解析法 曲线的设计—— ●4.4.1 滚子直动从动件盘形凸轮机构 ●4.4.2 滚子摆动从动件盘形凸轮机构理论轮廓 曲线方程 ●4.4.3 平底直动从动件盘形凸轮机构 ●4.4.4 滚子直动从动件圆柱凸轮机构 ● 4.5 凸轮机构基本尺寸的确定 ●4.5.1 凸轮机构的压力角和自锁 ●4.5.2 凸轮基圆半径的确定 ●4.5.3 滚子半径的选择 ●4.5.4 平底从动件的平底尺寸的确定 ● 小结

姓名：雷小舟班级：机制04班学号：1103010411利用VB绘制凸轮轮廓曲线及计算相关直角坐标和压力角VB程序语言如下：Private Sub Command1_Click()'参数初始化Dim r0%, r1%, h%, e%Dim a1%, a01%, a2%, a02%r0 = Val(InputBox("请输入基圆半径"))r1 = Val(InputBox("请输入滚子半径"))h = Val(InputBox("请输入升程"))e = Val(InputBox("请输入偏距"))a1 = V al(InputBox("请输入推程运动角"))a01 = Val(InputBox("请输入远休止角"))a2 = V al(InputBox("请输入回程运动角"))a02 = Val(InputBox("请输入近休止角"))Text1.Text = r0Text2.Text = r1Text3.Text = hText4.Text = eText5.Text = a1Text6.Text = a01Text7.Text = a2Text8.Text = a02Picture1.Scale (-75, 55)-(75, -55) '建立坐标系Picture1.Line (0, 50)-(0, -50)Picture1.Line (-55, 0)-(55, 0)'初始化参数Dim i!, j!, k!, m!, n!, l!Dim a!, b!, c!, d!, f!Const pi = 3.141592653Dim s#(360), s1#(360)Dim ds#(360), ds1#(360)Dim dx#(360), dy#(360)a = a1b = a1 + a01c = a1 + a01 + a2 / 2d = a1 + a01 + a2f = 360j = 0For i = 0 To a '推程段s(j) = h * (1 - Cos(pi * i / a1)) / 2ds(j) = h * pi * Sin(pi * i / a1) / (2 * a1)ds1(j) = ds(j) / 2s1(j) = s(j) / 2 '按比例定义参数值j = j + 1Next iFor i = (a + 1) To b '远休段s(j) = hds(j) = 0ds1(j) = 0s1(j) = s(j) / 2j = j + 1Next iFor i = (b + 1) To c '回程等减速段s(j) = h - 2 * h * (i - a1 - a01) ^ 2 / (a2 ^ 2)ds(j) = -4 * h * (i - a1 - a01) / (a2 ^ 2)ds1(j) = ds(j) / 2s1(j) = s(j) / 2j = j + 1Next iFor i = (c + 1) To d '回程等加速段s(j) = 2 * h * (a1 + a01 + a2 - i) ^ 2 / (a2 ^ 2)ds(j) = -4 * h * (a1 + a01 + a2 - i) / (a2 ^ 2)ds1(j) = ds(j) / 2s1(j) = s(j) / 2j = j + 1Next iFor i = (d + 1) To f '近休段s(j) = 0ds(j) = 0ds1(j) = 0s1(j) = s(j) / 2j = j + 1Next i'初始化参数'Dim X0#, Y0#, X1#, Y1#, X2#, Y2#Dim X11#, Y12#, X21#, Y22#Dim e1#, r#, p#, q#, r11#Dim s0#, a3#, a03#, a13#'按比例定义参数值'e1 = e / 2r = r0 / 2r11 = r1 / 2s0 = Sqr(r ^ 2 - e1 ^ 2)For i = 1 To 360dx(i) = (ds1(i) - e) * Sin(i * pi / 180) + (s0 + s1(i)) * Cos(i * pi / 180)dy(i) = (ds1(i) - e) * Cos(i * pi / 180) - (s0 + s1(i)) * Sin(i * pi / 180)Next i'输出理论、实际轮廓线图像及坐标值'X0 = e1: Y0 = s0For g = 2 To 360m = g - 1'求理论轮廓线X2 = (s1(g) + s0) * Sin(g * pi / 180) + e1 * Cos(g * pi / 180)Y2 = (s1(g) + s0) * Cos(g * pi / 180) - e1 * Sin(g * pi / 180)X1 = (s1(m) + s0) * Sin(m * pi / 180) + e1 * Cos(m * pi / 180)Y1 = (s1(m) + s0) * Cos(m * pi / 180) - e1 * Sin(m * pi / 180)Picture1.Line (X0, Y0)-(X1, Y1) '输出理论轮廓线图Picture1.Line (X1, Y1)-(X2, Y2)'求实际轮廓线p = dx(m) / Sqr(dx(m) ^ 2 + dy(m) ^ 2)q = -dy(m) / Sqr(dx(m) ^ 2 + dy(m) ^ 2)p1 = dx(g) / Sqr(dx(g) ^ 2 + dy(g) ^ 2)q1 = -dy(g) / Sqr(dx(g) ^ 2 + dy(g) ^ 2)X11 = X1 - r11 * qY12 = Y1 - r11 * pX21 = X2 - r11 * q1Y22 = Y2 - r11 * p1Picture1.PSet (X11, Y12) '输出实际轮廓线图'求压力角a3 = Abs(ds1(m) - e1) / (s1(m) + s0)a03 = Atn(a3) * 180 / pia13 = Abs(a03)If m Mod 5 = 0 ThenText9.Text = Text9.Text & " " & m & " " & 2 * X1 & " " & 2 * Y1 & " " & 2 * X11 & " " & 2 * Y12 & " " & a13 & " " & vbCrLf '每隔5°输出理论、实际轮廓线坐标值及压力角End IfX0 = X2: Y0 = Y2Next gEnd Sub代码编辑完成之后进行控件编辑，然后运行，图片如下：凸轮轮廓曲线图单独如下：（内轮廓为凸轮实际轮廓曲线，外轮廓为凸轮理论轮廓曲线）理论坐标值，实际坐标值及压力角分别如下：角度理论坐标X1值理论坐标Y1值实际坐标X11值5 13.3422488649574 37.7654699135133 8.00563520863182 29.3084873143164 （实际坐标Y12值）14.4275917751835 （压力角）10 16.6113888240431 36.6201626123094 10.5751606870804 28.6474623245437 14.339558604932415 19.8099518319073 35.2947136880551 13.1258634706131 27.856772926096 14.215485101277920 22.9390013468958 33.786344231391 15.6611472387024 26.9282949766938 14.058330151126625 25.9972138724791 32.0891892397401 18.1814385503099 25.8511081154383 13.871784760179430 28.9800857936919 30.1949810103691 20.6835375066202 24.6122140870338 13.660086810337735 31.8793010533959 28.0938923077854 23.16012077977 23.1973736101787 13.427821931222440 34.6822889682749 25.7755042172997 25.5994160643274 21.5920343882299 13.179727042232945 37.3719941167773 23.229858501982 27.985062991446 19.7823196627103 12.920510660411750 39.9268720143513 20.4485506973342 30.2961708002451 17.7560436639891 12.654700291199155 42.3211155304441 17.4258182420722 32.5075774448079 15.5037177655705 12.386522919833560 44.5251080223162 14.1595777289496 34.5903083545665 13.0195095021838 12.119820517459165 46.5060902965086 10.6523668774477 36.5122259542568 10.3021162405198 11.857999082007570 48.2290200895894 6.91215002731713 38.2388536146616 7.35551647082509 11.604007316102275 49.6575950992337 2.95295071320818 39.7343503575917 4.18956455652113 11.360339643560380 50.755403980713 -1.20471896705107 40.9626058162162 .820399328117849 11.129057760349385 51.4871644002125 -5.53365515911432 41.8884190713341 -2.72935700960609 10.911825094004390 51.8200034054071 -9.99999998471846 42.4787204023372 -6.43062582997395 10.709949172552195 51.7247331809868 -14.5635261361755 42.703791981655 -10.2481327730858 10.5244277665238100 51.1770747877666 -19.1781651797988 42.5384422811835 -14.1409011986077 10.3559955978335105 50.1587837607284 -23.792767386665 41.9630895289492 -18.0629684321482 10.2051692917602110 48.6586344217534 -28.3520722730608 40.964711941724 -21.9643060851593 10.0722890154272115 46.673224342148 -32.7978611078048 39.5376265682527 -25.7919176018107 9.95755586824093120 44.2075664047356 -37.0702557219873 37.6840642391778 -29.4910790189435 9.8610645632329125 41.2754431487963 -41.1091222946528 35.4145151038628 -33.0066830044075 9.78283127563007130 37.8995062720208 -44.8555345958003 32.74782726321 -36.2846417957369 9.7228167566893135 34.1111130150826 -48.2532486023801 29.7110497677609 -39.2733018642547 9.6809449397216140 29.9499003450573 -51.2501395609079 26.3390204055926 -41.9248220830537 9.65711732312722145 25.4631070496697 -53.7995534860555 22.6737079083436 -44.1964679178452 9.6512234212581150 20.7046627206483 -55.8615277280094 18.7633271119198 -46.0517766580646 9.66314754375353155 15.7572222888754 -57.4534880074477 14.6782501887699 -47.5118674550833 9.66314754387064160 10.6898598810582 -58.6081925519488 10.481462918737 -48.6103642524582 9.66314754387064165 5.54114118486271 -59.3168533627028 6.20490538704218 -49.3389068262703 9.66314754387064170 .350251058433762 -59.5740771030407 1.88112477874535 -49.6919505276289 9.66314754387064175 -4.84330469003621 -59.3779061449833 -2.45697232496655 -49.666808480794 9.66314754387064180 -9.99999996536154 -58.7298334679721 -6.77637038573203 -49.2636720319233 9.66314754387064185 -15.0745367207206 -57.5656111090232 -11.0309594505501 -48.4196019869985 9.7007343960619190 -19.9981704458301 -55.8275558531771 -15.1595919107961 -47.0760******* 9.76109683882332195 -24.6978957411788 -53.536768837998 -19.0962502669739 -45.252955224612 9.8448875174968200 -29.1036898513368 -50.7236867981278 -22.7778642759138 -42.9787574382612 9.95309952314434205 -33.149665708605 -47.4276717837425 -26.1454294146404 -40.2903982189764 10.0870993202687210 -36.7751707388143 -43.6964642540292 -29.1450765576733 -37.2325905867212 10.248674264752215 -39.9258158481975 -39.5855064328986 -31.7290786412417 -33.8571996010235 10.4400979065219220 -42.5544198533926 -35.1571445333176 -33.8567812466153 -30.2224629158374 10.6642177066071225 -44.6218556442095 -30.4797200758465 -35.4954454802181 -26.3921000447533 10.9245717745374230 -46.0977855692624 -25.6265620268804 -36.6209932859852 -22.4343201783329 11.2255440327002235 -46.961274894428 -20.67489284471 -37.2186474299426 -18.420738881855 11.5725712768119240 -47.2012736879912 -15.7046627303114 -37.2834608920572 -14.4252138861576 11.9724216180152245 -46.942835198741 -10.8560244008044 -36.9471992675453 -10.5606224187693 12.3336309643983250 -46.3399833366382 -6.22459690598456 -36.3636123320494 -6.91163517187719 12.681655391662255 -45.431669611272 -1.82061741740468 -35.569935142498 -3.47778164203514 13.0121159629415260 -44.2548453917153 2.35094281186775 -34.6000158015688 -.253719466668754 13.3204288555372265 -42.8438413668393 6.28984791720825 -33.483781229324 2.77000783247466 13.6019181075986270 -41.2298334709211 9.99999996352438 -32.2468376148195 5.60616502701814 13.8519513559864275 -39.4404020217594 13.4887864006403 -30.9102073318016 8.26999549168302 14.0660937671204280 -37.4991893417156 16.766384917381 -29.4901988911806 10.7783909324777 14.2402728080712285 -35.4256595978295 19.8450386466316 -27.9984018412384 13.1490814919631 14.3709442613559290 -33.2349630249241 22.7383149633246 -26.4417948741549 15.3998637319424 14.4552483369191295 -30.93790510528 25.460361226109 -24.8229530749793 17.5478798411627 14.491144224404300 -28.5410196900453 28.025********* -23.1403393798392 19.6089570917465 14.4775121886479305 -25.9898579223067 30.4060402745624 -21.3432501827544 21.5511525556394 14.4775121886479310 -23.2408976427484 32.5555014822271 -19.383725964433 23.3293307357039 14.4775121886479315 -20.3150600989574 34.4571956661558 -17.2766798873638 24.9299586223012 14.4775121886479320 -17.2346126813027 36.0966497853399 -15.0381478444566 26.3408544707334 14.4775121886479325 -14.0229994546489 37.4613866040076 -12.6851664162141 27.5512805116757 14.4775121886479330 -10.7046627348666 38.541019650922 -10.2356432120676 28.5520246720849 14.4775121886479335 -7.30485706805053 39.3273322666991 -7.70822058265609 29.3354706846372 14.4775121886479340 -3.84945702817411 39.8143401375464 -5.12213374028172 29.8956560521216 14.4775121886479345 -.36476029595861 39.9983368395049 -2.49706436732955 30.2283174256442 14.4775121886479350 3.12271248235638 39.8779220465728 .147009173219551 30.3309230512868 14.4775121886479355 6.58641953314425 39.4540121880325 2.78996388519434 30.2026920382836 14.4775121886479。

２ Ａ ｔＣ Ｄ辅助设 计 滚子 直 动 从动 件 盘 形 凸轮机 ｕ Ａ ｏ 构 的轮 廓 曲线方法
触 ， 以反转 后尖 底 的运 动轨迹 就是 凸轮轮廓 曲线 ， 所 图 １ 凸轮反转 法绘 图原理 。以下介绍 用 Ａ ｔＣ Ｄ 为 ｕｏ Ａ
山东省教育 厅 国 内访 问学者 资 助项 目（ 号 ： 编 鲁教 人 函
运动 ， 凸轮 以 等 角 速 度 顺 时 针 方 向 回转 ， 距 ｅ＝ 偏
２０ 年第 ６ ０８ 期
煤
矿
机
电
・ ５・ １
１ｒ 凸 轮 基 圆 半 径 ｒ ０ ｍ， ａ ０＝６ ｒ 滚 子 半 径 ｒ ０ ｍ， ａ ＝
１ｒ 。要求设计该机构凸轮轮廓曲线。 ０ｍ ａ （ ）绘制 位移线 图 １ 进入 Ａ ｔ Ａ ｕｏ Ｄ绘 图界 面 ， 制 位 移 线 图 ， 图 Ｃ 绘 作
Ｋ ｙ ｒ ｓ： ｃ ｍ ；ｍｏ ｉｇ ｃ ｒ ｅ ｕ ｌ ｅ ｃ ｒ ｅ ｄ ｓｇ ｅ ｗｏ ｄ ａ ｖｎ ｕ ｖ ；ｏ ｔ ｎ ｕ ｖ ｅ ｉｎ ｉ
凸轮 机构是 机械 传 动 中 的一 种 常用 机 构 ， 据 根 使用 要求 确定 凸轮机 构 的类 型 、 本 参数 以及从 动 基 件运 动规律 后 ， 即可 进 行 凸轮 轮 廓 曲线 的设 计 。设
关键 词 ： 凸轮 ； 动 曲线 ； 廓 曲线 ； 计 运 轮 设
中图分类号 ：Ｍ３ １Ｔ ５ ． Ｔ ５ ；Ｍ３９４
文献标 识码 ： Ｂ
文章 编号 ：０ １ ０７ （０ ８ ０ ０ １ ０ １０ — ８４ ２０ ）６— ０ ４－ ３
Ｄｅ ｉ ｆＣａ Ｃｕｒｅ Ｂａ ｅ ｎ Ａｕｏ ｓｇｎ ｏ ｍ ｖ ｓ ｄ ｏ ｔ ＣＡＤ
不 改变 ， 凸轮 固定不动 ， 但 机架 和从动件 一方 面 以角

凸轮曲线标注
凸轮曲线标注是在图纸或设计图中使用标注符号来表示凸轮的形状和特性的过程。

它用于描述凸轮轮廓的尺寸、形状、半径、角度以及凸轮上的特殊特征。

标注的方式可以根据具体要求和标准而有所不同，但一般包括以下几个要素：
1. 凸轮半径：标注凸轮起始点到中心轴线的距离，通常用字母R 和具体数值表示。

2. 凸轮轮廓尺寸：标注凸轮周长或轮廓曲线的关键点尺寸，如顶点位置、凹点位置、凸点位置等。

使用直线、箭头或特定符号表示。

3. 角度：标注凸轮上每个特殊点的角度，如凸轮头部朝向的角度、凸轮顶点相对于参考线的夹角等。

使用角度符号和具体数值表示。

4. 其他特征：标注凸轮上的其他特殊特征，如凸轮的凹凸形状是否对称、是否存在特定的边缘过渡等。

标注凸轮曲线的目的是为了确保制造过程中能够准确地理解和制造出与设计相符合的凸轮轮廓形状。

因此，标注应该清晰、准确，并符合相关的工程标准和约定。

具体的标注方式和标准应根据所处行业和地区而定，可以参考国际标准如ISO和ASME，或者根据企业内部的标准规范来进行。

广东工业大学华立学院课程设计（论文）课程名称机械原理课程设计题目名称对心直动平底从动件盘形凸轮机构的设计学生学部（系）机电工程学部专业班级10机械2班学号 (40)学生姓名~开指导教师2012年06月30日广东工业大学华立学院课程设计（论文）任务书一、课程设计（论文）的内容通过利用AutoCAD软件、AutoCAD二次开发技术绘制对心直动平底从动件盘形凸轮轮廓，用图解法进行对心直动平底从动件盘形凸轮机构的设计，计算出平底推杆平底尺寸长度，最后查验压力角是不是知足许用压力角的要求。

1）二、课程设计（论文）的要求与数据1.用图解法设计盘形凸轮机构，并用CAD画出凸轮轮廓。

2.用图解法设计盘形凸轮机构，并求出平底推杆平底尺寸长度。

3.按照从动件的运动规律计算出位移并绘画该曲线在图纸上；4.查验压力角是不是知足许用压力角的要求；5.编写课程设计说明书三、课程设计（论文）应完成的工作1.绘制对心直动平底从动件盘形凸轮轮廓机构的设计简图。

2.绘制出从动件的位移曲线图。

3.查验压力角是不是知足许用压力角的要求而且计算出平底推杆平底尺寸长度。

4.完成课程设计说明书。

四、课程设计（论文）进程安排五、应搜集的资料及主要参考文献[1] ]孙恒.机械原理（第七版）[M] .北京：高等教育出版社，2006[2]孙恒.机械原理（第六版）[M] .北京：高等教育出版社，2001[3]曹金涛.凸轮机构设计[M].北京：机械工业出版社，1985.[4]管荣法.凸轮与凸轮机构基础.[M] 北京：国防工业出版社，1985发出任务书日期：2012 年6 月16日指导教师签名：计划完成日期：2012 年6 月30 日教学单位责任人签章：目录(一).设计题目：对心直动平底从动件盘形凸轮轮廓机构的设计 (6)(二)凸轮轮廓曲线的设计的大体原理： (6)(三)运动规律分析： (7)(四)用作图法设计对心直动平底从动件盘形凸轮机构: (7)(五)计算平底推杆平底尺寸长度 (11)(六)压力角分析 (12)参考文献 (13)摘 要在凸轮轮廓曲线设计的图解法中应用AutoCAD 软件进行辅助设计和计算，维持了图解法原理简单、方式直观、易于掌握的长处。

（7）作直线族的内包络 线，既为所求凸轮 轮廓曲线。
60º
120º
1
180º
三、摆动从动件盘型凸轮机构凸轮廓线的设计
已知： 的转向，rb, lOA = a ，杆长L () ，设计轮廓曲线。
A8
A7
-
A9
max
A6 A5
B
8
B
7
A4
B
9
B12100° B0
rb
O
B1
aB
2
B180°B
5
4
3
C1 L
实+际(轮s0 廓+ s与)c理osφ论轮廓在 d法y/d线φ方= 向(ds处/d处φ 相– e等)c且osφ相距一 个滚子半– (径s0。+ s)sinφ
则理实论际轮轮廓廓曲曲线线上上点对B处应的点 C点法的线坐n-标n的：斜率：
tgxyCC ==ddxyB xBBB yrrrrcsdiodnsB xB y//dd
易使从动件得到各种预期的运动规律。
缺点：点、线接触，易磨损； 所以凸轮机构多用在传递动力不大的 场合。
§8—2 推杆的运动规律
直动从动件凸轮机构 s
行程
hs
A
rb
S
S
e
o
B
C 推程运动角
D
凸轮的基圆
该位置为初始位置
BC
S
近休止角
D 2
S
远休止角 回程运动角
基圆——以凸轮理论轮廓曲线最小矢径所作的圆。 行程——从动件由最低点到最高点的位移h（式摆角）。 推程运动角——从动件由最低位置运行到最高位置，凸
13
型腔
6（下冲头）
5 O3

因滚子中心的运动规律 是从动件的运动规律。
先作出凸轮的理论廓线， 再作其上滚子圆族的包 络线才能得到凸轮的实 际廓线。
r0
2)基圆半径r0 指的是凸轮的理论廓线的最小向径。
反转法原理
从动件 随机架反转（-）
又相对机架摆动
A
作复合运动
—
反转过程中，从动件转轴 A的运动轨迹是以凸轮轴心 O为圆心、中心距LOA为半 径的圆（转轴圆）。
在反转中，滚子中心 将描绘出一条与凸轮 廓线法向等距的曲线 (凸轮的理论廓线)。
凸轮的实际廓线是理论廓线上滚子圆族的包络线（与该 滚子圆族所有圆相切的曲线） 。
分析：机构“反转”时各构件间相对运动的几何关系
转角 i=∠C0OCi， 点 Ci为从动件的位置线 与基圆的交点。 从动件位移 Si= Ci Bi ， i=1,2，3… 基圆：以凸轮回转中心 O为圆心，以理论廓线的 最小向径为半径的圆。
一、凸轮廓线设计的基本原理
在图示的凸轮机构中，当凸轮 以等角速度 转动时，推动从 动件在导路中移动。
•为了在图纸上绘制出凸轮的 轮廓曲线，希望凸轮相对于 纸面保持静止不动，为此，采用 “反转法”。
反转法原理
设想给整个机构绕凸轮 转动中心O加上一个与 凸轮的角速度大小相等、 方向相反的公共角速度 （-）。 此时凸轮静止不动；
得诸点B1、B2、 …. 。
B1 B2
B10 B9
B3 B4 B5 B8
B6
B7
B1 B2
B10
B9 B3 B8
B4
B5
⑸将点B0、、B1 、 B2 …连成一条光 滑曲线，即得凸轮 的轮廓曲线。 （图中远休止段B6 、 B7间和近休止段 C11 、 C0间均为圆 弧）

凸轮轮廓曲线精度表示
在机械制造或工程模型中，凸轮轮廓曲线的精度表示通常使用以下几种方法：
1.尺寸公差：可以通过指定凸轮的关键尺寸公差来控制凸轮的
精度。

这包括凸轮的直径、半径、轮缘宽度等尺寸的公差要求。

2.几何公差：凸轮轮廓曲线的几何形状也可以通过公差来表示。

这包括凸轮曲线的凸度、倾斜度、曲率半径等几何特征的控制。

3.表面质量：除了尺寸和几何公差外，凸轮的表面质量也是衡
量其精度的重要指标。

可以通过指定表面光洁度、粗糙度和平面度等参数来表示凸轮表面的质量。

4.轨迹误差：凸轮轮廓曲线的精度还可以通过轨迹误差来表示。

轨迹误差是指实际凸轮轨迹与设计轨迹之间的偏差，可以通过测量实际曲线和理论曲线之间的差异来评估凸轮的精度。

综上所述，凸轮轮廓曲线的精度可以通过尺寸公差、几何公差、表面质量和轨迹误差等多种参数来表示。

具体的精度要求取决于具体应用和制造工艺的要求。

盘形凸轮轮廓设计的反转法原理简介盘形凸轮是一种常见的机械传动装置，用于将旋转轴的直线运动转换为旋转运动。

它由凸轮和随动件构成，通过凸轮轮廓的设计和随动件的运动，实现所需的机械运动。

反转法是一种用于盘形凸轮轮廓设计的常用方法，通过该方法可以快速、简便地设计出满足需求的凸轮轮廓。

反转法原理反转法是一种基于凸轮轮廓与随动件的相对运动关系的设计方法。

其基本原理是：1. 确定凸轮的旋转运动规律； 2. 确定随动件的运动规律； 3. 基于随动件的运动规律，反向确定凸轮的轮廓。

步骤一：确定凸轮的旋转运动规律首先，需要明确凸轮的旋转运动规律，即凸轮与旋转轴之间的运动关系。

常见的凸轮运动规律有恒速运动、简谐运动和等角加速度运动。

根据实际需求和设计要求，选择合适的凸轮运动规律。

步骤二：确定随动件的运动规律随动件是与凸轮配合的从动件，其运动规律由凸轮的轮廓决定。

通常，随动件的运动规律有平移运动、摆动运动和复杂曲线运动等。

根据实际需求和设计要求，选择合适的随动件运动规律。

步骤三：反向确定凸轮的轮廓在确定了凸轮的旋转运动规律和随动件的运动规律后，需要根据随动件的运动规律反向确定凸轮的轮廓。

具体步骤如下：1.将随动件的运动规律转换为凸轮轮廓上的点的运动规律。

对于平移运动的随动件，其轮廓上的点沿着一条直线移动；对于摆动运动的随动件，其轮廓上的点在一条曲线上摆动；对于复杂曲线运动的随动件，其轮廓上的点在一条复杂曲线上移动。

2.将凸轮轮廓上的点的运动规律转换为凸轮的轮廓。

根据随动件的轮廓上点的运动规律，确定凸轮轮廓上对应点的位置。

3.根据凸轮轮廓上的点的位置，绘制出完整的凸轮轮廓。

可以使用计算机辅助设计软件进行绘制，也可以手工绘制。

4.对设计的凸轮轮廓进行优化和调整，以满足实际需求和设计要求。

5.验证设计的凸轮轮廓是否满足要求，可以通过模拟运动或实际制作凸轮来进行验证。

适用范围反转法适用于设计盘形凸轮的轮廓，可以应用于各种工程领域，如机械工程、汽车工程、航空航天工程等。

０ 引言
凸轮轮廓 曲线是 由几段 函数 曲线组合 而成 的 ， 工程 实 际中通常 的设 计 方 法 有 图解 法 和 解 析 法 两 种． 图解 法 简
单、 便， 方 但作 图误 差较 大 ， 精度 较低 ， 用 于对 从 动件 运 适 动规律要 求不高 的一般精度 低速 凸轮设计 ； 于精 度要 求 对 高的高速 凸轮 、 模 凸轮 等 ， 须 用解 析 法列 出凸 轮 的轮 靠 必
Hale Waihona Puke ｌ Ａ ｔＣ Ｄ与 Ｅ ｃｌ 合快 速 精 确 地 绘 制 凸 ｕｏ Ａ ｘｅ 结
轮 曲线
Ａｔ Ａ ｕ Ｃ Ｄ是工程 界流行最 广泛 的二维绘 图软件 之一 ， ｏ
具有 良 的通用性、 好 简单易学 、 使用方便等特点 ， 对通常的
直线 、 圆弧 等的绘制 速 度快 且 精度 高． 对 曲线 的绘 制却 但 相对 较弱 ， 且涉及 到大 量 的坐 标计 算 时更 显 得笨 拙 ， 图 绘 速度 大大 降低 ． 如果 能将 Ａ ｔ Ａ ｕ Ｃ Ｄ的绘 图功 能与 Ｅｃｌ ｏ ｘｅ 的 列表计算 功能结 合起来 ， 先通 过 Ｅ ｃ 输 入所需 绘 制 的凸 ｘｅ ｌ
（） Ｂ ２ 在 ｌ中输入公式 ： ４ ５ ￥Ａ１ １０ Ｂ 格 内 ＝ ０＋ ０ ／５ ，１
线 ， 到各接触点再用 光 滑 的曲线 连上． 由于 凸轮各 段 找 但 曲线 的方程 是 已知 的 ， 容 易算 出曲线 上 各 点 的具 体 坐 很 标， 只不过这 些点是离 散 的． 于是 我们 可根 据作 图法 的基 本 原理 ， 于各段 凸轮 轮廓 曲线 方程 ， 对 给滚 动角 ａ 定一 设 个 微增 量 ｄ依 次求 出 ａ ａ ＋ｆ （ ＝ ， ，，） 点的 ， ＝０ ／ ｔ ， ０ Ｉ２３ 时 ． Ｘ Ｉ