当前位置：文档之家 › 弹性力学板弯曲

弹性力学板弯曲

  • 格式：pptx
  • 大小：464.45 KB
  • 文档页数：69

下载文档原格式

  / 69

合集下载

弹性力学：平板弯曲问题 (2) 薄板弯曲经典解法

弹性力学：平板弯曲问题 (2) 薄板弯曲经典解法

t
2
yz zdz
（10.10）
将式（10.3）和（10.5）代入式（10.9），（10.10）得
Mx
D
2w x2
2w y 2
,
My
D
2w y 2
2w x2
M
xy
D(1
)
2w xy
（10.11）
FQx
D
x
2w x2
2w y 2
,
FQy
D
y
2w x2
2w y 2
将式（10.3）和（10.5）与（10.11）进行比较， 可以得到用内力矩表示的薄板应力
D 4 w q
（10.7） （c） （10.8a）
即
4w x 4
2
4w x 2 y
2
4w y 4
q D
（10.8b）
方程（10.8）称为薄板的弹性曲面微分方程或 挠曲微分方程。它是薄板弯曲问题的基本方程。 从薄板中取出微元体进行平衡分析，同样可推导 出该方程式。
纵上所述，薄板弯曲问题归结为：在给定的薄 板侧面的边界条件下求解挠曲微分方程。求得挠 度w后，然后就可以按公式（10-3）、（10-5）和 （10-7）求应力分量。
薄板的小挠度弯曲理论，普遍采用以下三个计
算假定：
（1）、变形前垂直于中面的任一直线线段，变形 后仍为直线，并垂直于变形后的弹性曲面，且长度 不变。这就是Kichhoff的直法线假设；
（2）、垂直于板中面方向的应力分量σz、τzx 、 τzy较小，它们引起的形变可以略去不计，但它们本 身却是维持平衡所必须的，不能不计。
薄板弯曲问题的经典解法
第10章 薄板弯曲问题
在弹性力学中， 将两个平行面和垂 直于该平面的柱面 所围城的物体称为 平板，简称为板， y 如图10-1所示。

(整理)第6章弹性薄板小挠度弯曲问题的基础变分原理(16K)

(整理)第6章弹性薄板小挠度弯曲问题的基础变分原理(16K)

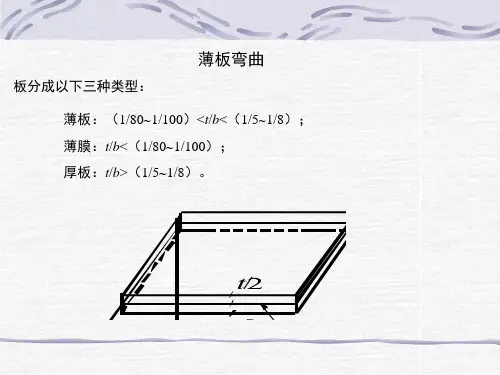
第6章 弹性薄板小挠度弯曲问题的基础变分原理平分板厚度的平面称为板的中面，一般地，当板的厚度t 不大于板中面最小尺寸的5/1时的板称为薄板，薄板的中面是一个平面。

薄板在垂直于中面的载荷作用下发生弯曲时，中面变形所形成的曲面称为弹性曲面或挠度面，中面内各点在未变形中面垂直方向的位移称为板的挠度。

薄板弯曲的精确理论应是满足弹性力学的全部基本方程，但这在数学上将会遇到很大的困难。

1850年，G.R.基尔霍夫（Kirchhoff Gustav Robert ，基尔霍夫 古斯塔夫·罗伯特，德国物理学家，1824-1887年）除采用弹性力学的基本假设外，还提出了一些补充的假设，从而建立起了薄板小挠度弯曲的近似理论。

这些假设是：第一，变形前垂直于板中面的直线，在板变形后仍为直线，并垂直于变形后的中面，而且不经受伸缩；第二，与中面平行的各面上的正应力z σ与应力x σ,y σ和xy τ相比属于小量；第三，在横向载荷作用下板发生弯曲时，板的中面并不伸长，这也就是说，薄板中面内各点都没有平行于中面的位移分量。

用变分法可以导出薄板弯曲问题的平衡微分方程和边界条件。

当板的形状和边界条件较复杂时，直接求解偏微分方程时比较困难的，以变分法为基础的各种近似解是求解这类问题的一个重要途径。

本章讨论了用于薄板小挠度弯曲问题的一些基础变分原理，这包括虚功原理、最小位能原理、最小余能原理、两类自变量广义变分原理并推广到三类自变量广义变分原理。

§6.1 基本方程与边界条件回顾取坐标平面oxy 与中面重合，z 轴垂直于中面，x ,y 和z 轴构成一个右手直角笛卡儿坐标系。

变形后的板内各点沿x ,y 和z 轴方向的位移分别用u ,v 和w 表示。

由Kirchhoff 假设，可以得到xwzz y x u ∂∂-=),,(，y w z z y x v ∂∂-=),,(，),(),,(y x w z y x w = （6-1）并利用弹性力学中位移与应变之间的关系式，可以得到薄板中任意点的应变分量为22x w z x ∂∂-=ε，22ywz y ∂∂-=ε，y x w z xy ∂∂∂-=γ22 （6-2）其余3个应变分量z ε,xz γ和yz γ根据假设都等于零，即0=εz ，0=γxz ，0=γyz （6-3）由薄板的平衡关系，可以确定板的横向分布载荷),(y x q 与剪力x Q ,y Q 以及弯矩x M ,y M 和扭矩xy M （x M ,y M ,xy M 统称为内力矩）与x Q ,y Q 之间的关系式。

弹性力学：平板弯曲问题的有限元分析(1)

弹性力学：平板弯曲问题的有限元分析(1)
其中为薄板的弯曲刚度9899薄板的弹性曲面微分方程薄板横截面上的内力称为薄板横截面上的内力称为薄板内力薄板内力是指薄板横截面的单是指薄板横截面的单位宽度上由应力合成的位宽度上由应力合成的主矢量主矢量和和主矩主矩
平板弯曲问题的有限元分析(1) Kirchhoff弹性薄板理论
参考文献： “弹性力学(下册)”第13章。徐芝纶
x
2w
2 (z2
2
2
)dz 4
E 3 12(1 2 )
x
2w
(c)
同样，在y为常量的截面上，每单位宽度内的 y , yx , yz
也分别合成如下的弯矩，扭矩，和横向剪力：
M y
2 2
z
y dz
E
12(1
3
2
)
(
2w y2
2w x2
)
(d)
M yx
2
2
z yxdz
E 3 12(1 2 )
(9-6)
( z )z q
(f)
2
将(9-6)式代入薄板上板面的边界条件：
得：
E
12(1
3
2
)
4
w
q
(9-7)
或 D4w q， (9-8)
其中
D
E
12(1
3
2
)
(9-9)
薄板的弹性曲面微分方程
为薄板的弯曲刚度
§9-３ 薄板横截面上的内力
► 薄板横截面上的内力，称为薄板内力，是指薄板横截面的单 位宽度上，由应力合成的主矢量和主矩。
对z积分，得到： z
2(1 2 )
2
( 4
z
z2 )4w 3
F3 (x,

薄板弯曲挠度计算公式

薄板弯曲挠度计算公式

薄板弯曲挠度计算公式全文共四篇示例，供读者参考第一篇示例：薄板弯曲挠度计算公式是工程力学课程中的重要内容，也是工程设计和结构分析中不可或缺的一部分。

薄板在受力作用下会发生弯曲变形，挠度是描述薄板弯曲程度的重要参数。

通过合理的挠度计算公式，我们可以准确地评估薄板的变形情况，为工程设计提供可靠的依据。

薄板弯曲挠度计算公式的推导过程比较复杂，需要借助数学和力学知识。

一般而言，薄板的挠度计算公式可分为静力法、弹性力学法和有限元法等多种方法。

静力法是最为常用的一种计算薄板挠度的方法，下面我们将对其进行详细介绍。

我们需要了解一些基本概念。

在工程力学中，对于一根长为L、宽为b、厚度为h的矩形薄板，在受到外力作用后呈弯曲状态，其挠度δ可以通过以下公式计算：\[ \delta = \frac{PL^3}{3EI} \]P为受力大小，E为杨氏模量，I为横截面惯性矩。

这是薄板挠度计算公式的一般形式，具体的计算过程需要根据实际情况进行适当的调整和修正。

静力法是一种比较简单但实用的计算挠度的方法。

该方法主要基于等效荷载原理，即将复杂的荷载系统转化为简化的等效荷载，将薄板弯曲问题转化为梁的弯曲问题。

下面我们以一种常见的简支边界条件情况为例，介绍具体的计算步骤。

假设我们有一根长为L、宽为b、厚度为h的矩形薄板，受到长度方向均布载荷q的作用，两端为简支边界。

我们需要计算该薄板的等效弯矩M，其计算公式如下：根据薄板挠度计算公式，我们可以得到该薄板的挠度表达式为：通过这个计算公式，我们可以快速准确地计算出简支边界条件下薄板的挠度。

如果有其他不同的受力情况或边界条件，需要进行相应调整。

除了静力法，弹性力学法和有限元法也是常用的计算薄板挠度的方法。

弹性力学法是以弹性理论为基础，考虑了薄板材料的应力应变关系，可以更精确地描述薄板的弯曲情况。

有限元法则是一种数字计算方法，通过将薄板离散成有限个单元，利用计算机进行大规模计算，可以处理更加复杂的挠度计算问题。

弹性力学圆形薄板

弹性力学圆形薄板

xz
Qx
t Ez 2 2 2 t 2 可得 Qx w t z dz 2 1 x 4 2
z d zx
Et 3 2 w 12 (1 ) x
t 2 t 2

x
Q
同样可得Qy,
记 可得
Et 2 D 12 (1 2 )

x z 0
0, 0
y z 0 xy z 0
0,
也就是说，中面的任意一部分，虽然弯曲成 弹性曲面的一部分，但它在xy面上投影的形 状却保持不变。
二、弹性曲面的基本公式
1、弹性曲面的微分方程。 薄板的小挠度问题是按位移求解的，其基 本未知函数是薄板的挠度ω 。因此把其它 所有物理量都用ω 来表示，即可得弹性曲 面的微分方程。
z t 2
3、边界条件
边界上的应力边界条件，一般难于精确满足， 一般只要求满足边界内力条件。 情况一：以矩形薄板为例，说明各种边界处 的边界条件。假设OA边是固支边界， 则边界处的 挠度和曲面的法向斜率等于零。即

x 0
0,
0 x x 0
情况二：OC具有简支边界。则边界处的挠度 和弯矩等于零。即：
y xz yx z x y
即
z Ez t2 2 z 4 w z 2(1 2 ) 4 Ez z3 4 t2 z z w F3 ( x, y ) 2 2(1 ) 4 3
积分得
根据薄板下面内的边界条件：
圆形薄板轴对称 弯曲问题
主要内容：
一、有关概念及假定

二、弹性曲面的基本公式 三、圆形薄板轴对称弯曲问题的求解

《弹性力学》第十二章薄板弯曲

《弹性力学》第十二章薄板弯曲

4w q D
得:
C
q0
8D
3 a4

2 a 2b 2

3 b4

从而
w
q0 1
x2 a2

y2 b2
2

8D
3 a4

2 a 2b 2

3 b4

内力
M
x

D
2w x2


2w y 2


4CD


3x2 a4

xy

8CD1


xy a 2b 2
最大挠度为: wmax x0,y0 C
最大弯矩为（设a>b):
Mmax
My
x0, y b
8CD b2
其中
C

8D
3 a4
q0

2 a2b2

3 b4

,D

Et3
12 1 2
28
例2 试求图示四边简支，
承受均布载荷 q0 的矩形
o
q0
薄板之最大挠度。
x
z
解：取图示坐标系
设
w

m1
Ym
y
sin
mx
a
a
b
则在x=0及x=a边界上，边
o
2
界条件
w 0,
自然满足。
2w x 2

0
b
x
2
y
将w 的表达式代入弹性曲面微分方程
4w q D
29
得
Ym4
m1

薄板弯曲问题

薄板弯曲问题

略不计。取 εz =0
，因而有：
• 因此，板内各点的挠度w 与z 坐标无关，只是x、y 的函数。
• 2. 直线假设
• 在薄板弯曲变形前垂直于板中面的直线，在簿板弯曲变形后仍为直线， 且垂直于弯曲后的中面。这说明在平行于中面的面上没有剪应变，即：
上一页 下一页 返回
7.1 薄板的弯曲变形
• 3. 正应力假设 • 中面上的正应力远小于其他应力分量的假设：平行于中面的各层相互
上一页 下一页 返回
7.2 矩形薄板单元分析
• 最后两项的选取是使单元在边界上有三次式的形式。按照式（7.20） 可以算出转角，即：
上一页 下一页 返回
7.2 矩形薄板单元分析
• 将矩形单元的4 个节点坐标(ξ i , η i ) 分别代入式（7.20），就可以得 到用12 个参数来表示的节点位移分量的联立方程组，求解这12 个方 程，从中解出a1～a12，再代入式（7.21），经归纳并整理后就可以改 写成如下的形式：
• 或者写成标准形式，即：
上一页 下一页 返回
7.2 矩形薄板单元分析
• 其中 • 如果把形函数写成通式，即：
上一页 下一页 返回
7.2 矩形薄板单元分析
• 于是有：
• 其中，
上一页 下一页 返回
第八章 班级气氛的经营与管理
• 知道最好的一切，且将之发挥至极致，才 是成功的生活。
• 未来我们会创造一个更经济、更有效率的 世界，但是让人担心的是，人们却没有现 在过得幸福。
• 为学生营造良好的班级气氛，提供给学生优质的 学习和生活环境，让学生快乐、健康地在班级中 成长是班级管理者的义务和责任。
2022/8/29
24
一、班级气氛的涵义与作用

板弯曲详细讲解

板弯曲详细讲解

2 －t
2
Zdt
板上、下表面的边界条件变成
z zt 0 2
z z－t q 2
z z
2(1
E
v
2
)
t2 4
z2
2 w
z
Et 2(1
3
v
2
)
t2 4
z
z3 3
4w
f
(x,
y)
利用板下面的边界条件 z zt 0 ， f(x,y)=0 2
z
Et 3 1
6(1
v
2
)
2
-
z 2 1 t
垂直于中面的位移称为挠度w。小挠度弯曲问题
▪ 薄膜：
其抗弯的能力很低，可认为其抗弯刚度为零，横向荷载由板面内的轴向力 和板面内的剪切力来承担；
▪ 厚板：
其内部任意点的应力状态与三维物体类似，难以进行简化，应按照三维问 题处理；对于厚度比较小的薄板。
▪ 薄板的基本假定：
（1）板中面法线变形前是直线，变形后仍保持直线，且与变形后的中面 保持垂直；
力就是支座对板角点的集中反力。在求得挠度后，这个集中力可由式求得 对于无支座支撑的角点，例如图中的两自由边界的交点B，则要求
即：
RB =2(Myx)x=a, y=b = 0，
2w xy
xa,
y b
0
2w x 2
2w y 2
特点：
y
1
Ez
2
2w y 2
2w x 2
xy
Ez 1
2w xy
均沿厚度呈线性分布，在中面处为零，
在板的上、下板面达到最大。
zx x yx z x y
zy y xy z y x

弹性力学第八薄板弯曲剖析

弹性力学第八薄板弯曲剖析

§8-2 弹性曲面的基本公式
一、弹性曲面的微分方程
薄板的小挠度问题是按位移求解的，其基本未知函数是薄 板的挠度w。因此把其它所有物理量都用w来表示，即可得弹 性曲面的微分方程。
由假设
zx 0 , yz 0
可得： u w 0 z x
w v 0 y z
即 u w v w z x z y
由几何方程可得 w 0, w w x, y
z
在中面的任意一根法线上，薄板全厚度内所有各点都具 有相同的位移，其值等于挠度。与梁的弯曲相似，在梁的任 意一横截面上，所有各点都具有相同的位移，其值等于轴线 的挠度。
（2）应力分量 zx , zy 和 z 远小于其余三个应力
分量，因而是次要的，它们所引起的形变可以不计。但它 们本身是维持平衡所必需的，不能不计。所以有：
z
xy
u y
v x
2
2w xy
z
由物理方程可得
x
Ez
1
2
2w x 2
2w y 2
y
Ez
1
2
2w y 2
2w x 2
xy
Ez
1
2w xy
另由平衡方程可得
zx x yx
z
x y
zx
z
Ez
1 2
3w x3
3w xy2
1
Ez
2
2w x
zy y xyx
( x
y)
y
1 E
(
y
x )
xy
1 G
xy
2(1
E
) xy
（3）薄板中面内的各点都没有平行于中面的位移，即：
u z0 0,
z0

弹性薄板的小挠度弯曲课件

弹性薄板的小挠度弯曲课件
践指导。
06
参考文献
参考文献
总结词：详细描述了弹性力学的基本 原理，包括应力和应变的关系，以及 弹性薄板在受到外力作用时的弯曲变 形规律。
详细描述：在弹性力学中，薄板的小 挠度弯曲是指薄板在受到外力作用时 发生的弯曲变形，其弯曲变形程度较 小，可以忽略不计薄板的剪切变形和 转动惯性。这种变形情况下，薄板的 弯曲变形可以通过挠度（即变形量） 来描述。在弹性力学中，应力和应变 之间的关系由胡克定律（Hooke's Law）描述，即应力与应变成正比， 比例系数为材料的弹性模量。
详细描述
圆形薄板在受到垂直于其平面的力时，会在力的方向上发生弯曲，形成弧形。与矩形薄板类似，这种弯曲程度较 小，也称为小挠度弯曲。在圆形薄板中，各个方向的弯曲程度基本相同，因此圆心位置的应力最大。
实例三：不规则形状薄板的弯曲
总结词
不规则形状薄板在受到垂直于其平面的力时，会发生小挠度弯曲。
详细描述
不规则形状薄板在受到垂直于其平面的力时，会在力的方向上发生弯曲，形成弧形。与矩形和圆形薄 板类似，这种弯曲程度较小，也称为小挠度弯曲。不规则形状薄板的弯曲情况较为复杂，需要考虑各 个方向的弯曲程度以及应力分布。
05
结论与展望
研究结论
结论一
弹性薄板在受到小挠度弯 曲时，其弯曲行为与材料 属性、几何尺寸等因素密 切相关。
结论二
通过理论分析和数值模拟， 我们得到了弹性薄板在小 挠度弯曲下的变形规律和 应力分布。
结论三
实验结果与理论预测和数 值模拟结果基本一致，验 证了理论的正确性和数值 方法的可靠性。小的单元，对每 个单元进行弯曲分析，通过求解每个 单元的平衡方程得到整体的挠度分布。
对于某些特定形状和载荷条件的薄板， 可以通过解析方法直接求解弯曲微分 方程，得到挠度分布的精确解。

弹性力学10塑性极限分析

弹性力学10塑性极限分析

Pl
Mp l
ql 2 Mmax 2 M P
ql
2M p l2
❖ 例：确定下列静定梁的极限载荷。
（3） A
q
l/2 B l/2 C
ql2/2
ql2/8
AB：3Mp BC：Mp
解：
AB与BC段截面不同，塑性 铰可能出现在AB段也可能出 现在BC段。
作弯矩图。
塑性铰出现在AB段时：
M max
ql 2 2
证明： k l
设机动允许的位移（速度）场 u * i
q ij*
破坏载荷： k Pi 应力场： s * ij
❖ 虚功率原理：
k Piui*dS
s
*
ij
i*j
dV
ST
V
s*
s s ij
*
ij
ij
s ij
l Piui*dS s iji*jdV
ST
V
k l
Piui*dS
s* ij
3MP
塑性铰出现在BC段时：
MB
ql 2 8
MP
ql
6M p l2
ql
6M p l2
ql
8M l2
p
二．超静定梁的极限分析
❖ 超静定结构的基本特点： （1）有多余联系，内力仅由静力平衡方程不能完全确定，内力与结 构的变形有关，所以内力与梁的刚度有关。
（2）在超静定梁中，当梁内截面屈服，即出现塑性铰时，由于梁的 刚度发生变化，内力会重新分布，所以梁达到塑性极限状态时塑性 铰的位置无法预先知道，应按照逐渐加大载荷的方法逐步确定，但 计算不便。
ST
V
q ij
s ij
s0 ij
s ij

弹塑性力学6薄板弯曲

弹塑性力学6薄板弯曲
x
Mxy
Mx
z
My
Myx
Qx
y
Qy
• 内力由挠度表示
将应力的表达式代入积分得到
M
x


D(
2w x 2

v
2w y 2
)

D(K x

vK
y
)
M
y


D(
2w y 2

v
2w x 2
)

D(K
y

vK x
)
M
xy

M
yx

D1 2w
xy
Qx

D 2w x
利用板下面的边界条件 z zt 0 ， f(x,y)=0
2
z


Et 3 6(1 v2 )

1 2
-
z t
2
1


z t
4w
z沿板厚度方向呈三次方变化 最大值发生在板面为q，最小值在板底为0。
• 薄板的平衡微分方程
利用板上面的边界条件 z zt q ，得：


m1,3,5... n1,3,5...
m2 a2

n2 b2
mn(
m2 a2

n2 b2
)2
sin
mx
a
sin
ny
b
M y
16q0 4


m2 a2
2
mn( m m1,3,5... n1,3,5...

n2
b2 n2 )2
sin
mx sin a
ny b

弹性力学第九章 薄板弯曲问题

弹性力学第九章 薄板弯曲问题

NORTHEASTERN UNIVERSITY
§9－3 薄板横截面上的内力
（1）应力分量 x
由公式（9－4）知， x 合成的主矢量为零；
对中面合成的弯矩
2
M x 2 z xdz
把（9－4）代入上式
M x


1
E

2

2w x2


2w y2

2 z2dz
§9－1 有关概念及计算假定
计算假定：
薄板的小挠度弯曲理论，三个计算假定。
（1）垂直于中面方向的正应变可以不计。即
z 0
由几何方程可得
y
w 0, w w x, y
z
0
x
b
/2 /2
z 图9－1
也就是说，在中面的任意一根法线上，薄板全厚度内所有各点都 具有相同的位移，其值等于挠度。
M yx
2 2
z yxdz

E 3
121
2w xy

M xy
Fsy
2


2
yz
dz

12
E 3 1 2
2w y
（d） （e） （f）
弹性力学简明教程
NORTHEASTERN UNIVERSITY
§9－3 薄板横截面上的内力
zx 0, yz 0
这里与梁的弯曲相同之处，也有 不同之处，梁的弯曲我们只考虑横截 面，板的弯曲有两个方向，要考虑两 个横截面上的应力。
弹性力学简明教程
NORTHEASTERN UNIVERSITY
§9－1 有关概念及计算假定
结合第一假定，可见中面的法线在薄板弯曲时保持不伸缩，并且成 为弹性曲面的法线。

弹性力学第9章—薄板的弯曲

弹性力学第9章—薄板的弯曲
b
O
a
x
z
y
边界条件
( w) x =0,a ( w) y =0,b ⎛∂ w⎞ =0 ⎜ 2 ⎟ =0 ⎝ ∂x ⎠ x =0,a
2
因为任意的荷载函数q总能展 开成双重三角级数，因此纳维解的 基本形式为
∞
⎛ ∂2w ⎞ =0 ⎜ 2 ⎟ =0 ⎝ ∂y ⎠ y =0,b
mπ x nπ y sin w = ∑ ∑ Amn sin m =1 n =1 a b
9.3 薄板的边界条件
薄板的边界条件可以分为以下三类， （1）位移边界条件，即在边界上给定挠度和转角； （2）静力边界条件：给定边界横向剪力、弯矩； （3）混合边界条件：在边界上同时给定广义力和广义位移。
9.3.1 固定边界
x
y
x
侧视图
( w ) x =0 = 0
⎛ ∂w ⎞ ⎜ ⎟ =0 ⎝ ∂x ⎠ x =0
⎫ ⎪ ⎬ ⎪ ⎭
俯视图
9.3 薄板的边界条件
9.3.2 简支边界
x
y
x
侧视图
⎫ ( w ) x =0 = 0 ⎪ ( M x ) x =0 = 0 ⎬ ⎪ ⎭
俯视图
将上式中的弯矩用挠度函数来表示，则有
( w ) x =0 = 0
⎛ ∂2w ⎞ ⎜∂ 2⎟ ⎝ x ⎠ x =0
⎫ ⎪ ⎬ = 0⎪ ⎭
9.3 薄板的边界条件
9.3.3 给定广义力的方案
x
x=a
侧视图 俯视图 以广义力为零的自由边界为例，x=a处的边界条件为
⎪ ⎪ M 0 = ( xy ) x=a ⎬ ⎪ (Qx ) x =a = 0 ⎪ ⎭
( M x ) x =a = 0 ⎫
其中第1式分布弯矩可以根据 M x = D (κ x + vκ y ) 用挠度函数表示

高中物理实验测量弹性系数的方法

高中物理实验测量弹性系数的方法

高中物理实验测量弹性系数的方法在高中物理实验中，测量弹性系数是一项常见的实验。

弹性系数是衡量材料弹性特性的一个重要参数，也是弹性力学的基本概念之一。

正确地测量弹性系数对于理解和应用弹性力学知识至关重要。

本文将介绍几种常用的方法来测量材料的弹性系数。

一、悬挂法悬挂法是一种测量弹性系数的简单而有效的方法。

实验中，首先需要准备一个弹簧或橡胶条，将其悬挂在一个固定的支架上。

然后，挂载一定质量的物体在弹簧或橡胶条下方，并测量物体的下垂长度。

根据胡克定律，弹簧或橡胶条的伸长量与挂载物体的质量成正比。

通过改变挂载物体的质量，可以得到不同的伸长量，进而计算出相应的弹性系数。

二、杨氏模量法杨氏模量法是一种精确测量弹性系数的方法。

实验中，需要使用一个长而细的材料试样，并在试样上施加一个小的拉力。

通过测量试样的伸长量和应力，可以计算出杨氏模量。

具体的实验步骤是：首先，固定一个端点，用一具有刻度的尺子固定在试样上；然后，施加恒定的拉力，记下尺子上的刻度差值；最后，测量试样的初始长度，并计算出试样的伸长量和应力，进而得到杨氏模量。

三、声速法声速法也是一种测量弹性系数的方法。

实验中，需要使用一个材料棒，并通过敲击或撞击产生声波。

通过测量声波在材料中传播的时间间隔和材料的长度，可以计算出材料的声速。

根据声速和杨氏模量之间的关系，可以反推出材料的弹性系数。

四、弯曲法弯曲法是一种测量材料弹性系数的常用方法之一。

实验中，需要使用一个长而薄的材料板，并通过施加一个或多个力矩来使其弯曲。

通过测量板的挠度和施加的力矩，可以计算出材料的弹性系数。

弯曲法适用于不同形状和材料的物体，如梁、梁板等。

综上所述，测量弹性系数的方法有悬挂法、杨氏模量法、声速法和弯曲法等。

在进行这些实验时，需要注意实验条件的稳定性、仪器的准确度和数据的精度。

只有在严格控制这些因素的情况下，才能得到准确可靠的实验结果，进而更好地理解和应用弹性力学知识。

通过实验探究和测量弹性系数，不仅可以加深对弹性力学理论的理解，也为相关应用提供了依据和指导。

圆环截面的变形量材料科学

圆环截面的变形量材料科学

圆环截面的变形量材料科学
圆环截面的变形量可以用弹性力学中的板弯曲理论进行计算。

材料科学方面，需要考虑材料的弹性模量、泊松比等参数的影响。

当圆环受到外力作用时，其上下表面都会发生弯曲变形，而且外侧受力最大，内侧受力最小。

假设圆环截面半径为r，厚度为t，外界施加一个垂直于圆环平面的载荷F，则会产生一个形心位移量w，可以用以下公式计算：
w = F * r^2 / (2 * E * t)
其中，E为材料的弹性模量。

该公式表明，圆环的弯曲变形量与其整体尺寸、载荷大小以及材料的弹性模量等有关。

如果材料的弹性模量较小，则圆环的弯曲变形量也会相应变小。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

（x，y，xy）～qb2/t2
（xz，xz y）～qb/t
z～q

由内力表示的平衡微分方程
Qx Q y q0 x y M x M yx Qx 0 x y M xy x M y y Qy 0
2 M xy 2 M y 2M x 2 q0 2 2 x xy y
Qy D

应力与内力的关系
x 12 z Mx 3 t y 12 z My 3 t xy 12 z M xy 3 t
yz
6 t ( z 2 )Q y 3 t 4
2
6 t2 zx 3 ( z 2 )Qx t 4
1 z z z 2q ( ) 2 (1 ) 2 t t
（3）中面各点没有平行于中面的位移。

假定的推论
假定（2）（与梁弯曲问题的互不挤压假定相似）
z=0
z w 0 z
w=w(x,y)
假定（1）（与梁弯曲问题的平面假定相似） zx=zy=0，
w u y ＋ ＝0 y z
w ux z f1 x, y x
w u x ＋ ＝0 x z
RB＝(Myx)B＋(Mxy)B＝2(Myx)B
3w 3w Vx D 3 ( 2 v ) xy 2 x 3w 3w V y D 3 (2 v) 2 x y y
2w RB 2 D(1 v)( ) xy
d 4w 2 q ( x) 1 EI dx 4
与梁的平衡微分方程相比，多了一项（12）。 其原因是：板单位宽度的窄条是处于平面应变状态（y=0）



薄板横截面上的内力
M x z x dz M xy
t 2
t 2 t 2 t 2 t 2
x
z xy dz
xz x z xy yx y
2w 0 xy xa, y b
w 0 x x0
即：
例7-1：受均匀分布荷载四边简支板的Navier解 解：设挠度为三角级数形式 ny mx w Amn sin sin a b 它能满足所有的边界条件，即
(w) x=0=0
考虑薄板上、下板面的边界条件
zy y xy z y x
zy z t
解得横向剪应力
0
2
zx z t 0
2
E 2 t2 2 z zx w 2 4 x 21
E 2 t2 2 z zy w 2 4 y 21
(w) x=a=0
(
w ) 0 2 x 0 x
2
(w) y=0=0 (w) y=b=0
2w ( 2 ) y 0 0 y
2w ( 2 ) y b 0 y
2w ( 2 ) xa 0 x
利用三角级数的正交性，求得
ny mx q cmn sin sin a b
利用板下面的边界条件 z z t q ，得：
2
Et 3 4 wq 2 12(1 )
Et 3 D＝ 12(1 v 2 )
D是板的弯曲刚度，板厚的三次方成正比，与弹模成正比， 与梁的弯曲刚度类似
D4 w q

薄板的柱面弯曲
矩形板一个方向（比如y方向）足够长，
分布荷载沿y方向不变化，只沿x方向变化，即q=q(x)时，则 w=w(x) 板弯曲成柱面，取单位宽度的窄条（梁）分析。平衡方程退化为
利用板下面的边界条件
z z t 0 ，
2
2
f(x,y)=0
Et 3 1 z z 4 z - 1 w 6(1 v 2 ) 2 t t
特点：
z沿板厚度方向呈三次方变化
最大值发生在板面为q，最小值在板底为0。

薄板的平衡微分方程
2w y z 2 y y u y
xy
x=Kxz
y＝Kyz
xy＝2Kxyz
z = yz = zx ＝0
e a
z
b
c
y
2w Kx 2 x
2w Ky 2 y
d
K xy
2w xy

薄板的应力分量
( x、y、xy）通过平面问题的物理方程由应变求出
ny mx sin sin 16q 0 a b w 6 D m 1,3,5... n 1,3,5... m2 n2 2 mn( 2 2 ) a b

16q Mx 6 0 D
m 1, 3, 5... n 1, 3, 5...




m2 n2 2 ny mx a2 b sin sin a b m2 n2 2 mn( 2 2 ) a b

薄膜：
抗弯的能力很低，可认为抗弯刚度为零 横向荷载由板面内的轴向力和板面内的剪切力来承担

厚板：
内部任意点的应力状态与三维物体类似，难以简化，应按三维问题处理

薄板
可以引进基本假定，使问题简化。

薄板基本假定
（1）板中面法线变形前是直线，变形后仍保持直线，且与变形后的中面
保持垂直；
（2）中面法线变形后既不伸长也不缩短；
2w 2w y 2 x 2 ＝0 y b
3w 3w y 3 (2 v) x 2y ＝0 y b
（2）简支边 在y=0的简支边界上，挠度和弯矩应为零
2w 2w (w) y=0=0， (My) y=0＝ y 2 x 2 0 y 0
t 2
Qx t zx dz
2
yz y
My
t 2
t z y dz 2
M yx
t 2
z yx dz
Qy
t 2
t zy 2
dz
• 剪应力互等定理 xy = yx，
Mxy=Myx
• 正负规定：在z为正，若应力分量为正，则由此合成的内力为正 • 内力是作用在每单位宽度上的力，例如： 弯矩和扭矩的量纲应是［力］，而不是通常的［力］［长度］。


cos
ny mx cos a b m2 n2 2 ( 2 2) a b
在板的中心x=a/2，y=b/2处，挠度最大，弯矩Mx和My最大， 而Mxy为零；在板边Mx和My为零，而Mxy最大。
z z t 0
2
z z －t q
2
z E t2 2 2 z w 2 z 2(1 v ) 4
Et 3 t 2 z3 4 z z w f ( x, y ) 2 3 2(1 v ) 4

侧边边界条件
自由边、简支边、固定边、角点 用挠度表示
O C
x
b
A y
a
B
（1）自由边 弯矩和合成剪力为零，因此，
在x=a上， Mx=0，Vx＝0， 在y=b上，My=0，Vy＝0，
2w 2w x 2 y 2 ＝0 x a
3w 3w x 3 (2 ) xy 2 ＝0 x a

薄板问题求解
D4w=q ＋ 侧边边界条件
• 侧边边界条件由圣维南原理满足
• 将分布剪力和分布扭矩合成为分布剪力
x
C z A y B

分布剪力和分布扭矩合成
M y x
M yx M yx dx x
( M ) y x B
B
A M ( ) A y x d x d x
• 可用2个大小相等为Myx，方向相反，相距dx的垂直力代替 • 可用2个大小相等为 M yx
M yx dx ，方向相反，相距dx的垂直力代替 x
Vy Qy
此外，还有两端未抵消的集中剪力
M yx x
RA＝(Myx)A， RB＝(Myx)B
Vx Qx
M xy y
及两端的集中力
RB＝(Mxy)B，RC＝(Mxy)C
O RB A y RA z B RC C x
最终角点B出现未抵消的的集中力应是
薄板弯曲
• 板分成以下三种类型：
薄板：（1/801/100）<t/b<（1/51/8）； 薄膜：t/b<（1/801/100）； 厚板：t/b>（1/51/8）。
x
t / 2
t / 2

板所承受的荷载：
作用于中面的面内载荷。弹性力学平面问题
垂直于中面的横向荷载。板产生弯曲，中面弯曲将成为一个曲面， 垂直于中面的位移称挠度w。小挠度弯曲问题
( z、zx、zy）则必须由三个平衡微分方程求解给出
应力分量（z、zx、zy）相对面内应力分量（x、y、xy）很小
它们对应的应变分量z、zx、zy可略去不计
但它们本身由于是平衡所必须的而不能忽略不计。

面内应力分量（x、y、xy）
Ez 2 w 2w 2 2 x 1 2 x y
x
z
My Mxy Myx Qy
2w 2w M x D( 2 v 2 ) x y
2w 2w M y D( 2 v 2 ) y x
M xy M yx
2w D 1 xy
Qx D
2 w x
2 w y
Ez 2 w 2w 2 2 y 2 1 y x
Ez 2 w xy 1 xy
特点： 均沿厚度呈线性分布，在中面处为零， 在板的上、下板面达到最大。

面外应力分量
使用平衡条件求出
zx x yx z x y