基本条分法

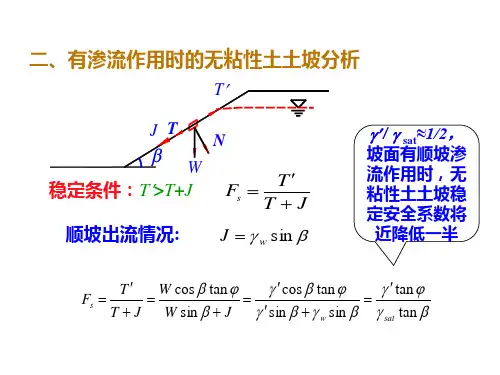
瑞典条分法的具体步骤
嘿，咱今儿就来聊聊瑞典条分法的具体步骤哈！这瑞典条分法啊，就像是搭积木，一块一块地把复杂的问题给拼凑清楚。

首先呢，咱得把要研究的土体划分成一条条的小块儿，就跟切蛋糕似的，可别切得乱七八糟哦！这每一条小块都有它自己的作用呢。

然后呢，就得考虑这些小块之间的作用力啦。

想象一下，它们就像是一群小伙伴，互相之间有着各种牵扯和影响。

要仔细分析它们之间的摩擦力、重力啥的，可不能马虎。

接下来呀，计算每一条土条的重量。

这可不能算错喽，不然整个分析可就都错啦。

就好像走路，一步错步步错呀！
再之后呢，根据那些力呀重量呀，来计算整个土体的稳定性。

这就像是给土体做个全面的“体检”，看看它到底稳不稳固。

接着说哈，还得反复调整那些土条的划分和参数，就跟调整收音机的频道似的，直到找到最合适的那个状态。

咱再想想啊，这瑞典条分法不就是个厉害的工具嘛，能帮咱搞清楚土体的各种情况。

就好比你有一把神奇的钥匙，能打开土体秘密的大门。

你说，要是没有这瑞典条分法，咱咋能这么清楚地了解土体呀？它就像是黑暗中的一盏明灯，给咱指引方向呢！而且呀，学会了它的具
体步骤，咱就像是掌握了一门独特的技能，在工程领域里那可就能大
显身手啦！
咱可别小瞧了这瑞典条分法的每一个步骤哦，每一步都得认真对待，就像对待宝贝似的。

要是有一步出了差错，那后果可不堪设想啊！
总之呢，瑞典条分法的具体步骤虽然有点复杂，但只要咱用心去学，去理解，就一定能掌握得牢牢的。

到时候，咱就能在土体分析的世界
里自由驰骋啦，哈哈！。

bishop条分法
Bishop条分法是一种机器学习算法，被广泛应用于分类问题中。

它通过将数据分割成若干个区域，每个区域对应一个分类标签，从而实现对数据的分类。

Bishop条分法的基本思想是：将数据的特征空间划分成若干个区域，每个区域对应一个分类标签。

对于新的数据样本，将其分类至对应的区域，即可得到其所属分类。

此外，Bishop条分法可以通过最小化分类错误率来确定最优的划分方式。

1.数据的预处理：包括数据的归一化处理、特征选择、降维等过程。

2.特征空间的划分：将特征空间划分成若干个区域，每个区域对应一个分类标签。

在Bishop条分法中，通常采用决策树或支持向量机等方法进行划分。

3.模型的训练：利用已知的训练数据，确定最优的划分方式和相应的分类标签。

这通常需要通过训练数据的预测精度来评估模型的表现，并不断调整参数以提高分类的准确率。

4.模型的测试：对测试数据进行分类，根据分类的结果来评估模型的准确性。

Bishop条分法的优点是计算量较小，分类效果较好，且可以处理多分类问题。

然而，由于其使用的是基于区域的分类方式，因此对于决策边界比较复杂的问题，其效果可能不如其他分类算法，如神经网络等。

此外，Bishop条分法的主要缺陷是对于特征空间划分的依赖性较强，需要人工进行调整和优化。

总的来说，Bishop条分法是一种简单而有效的分类算法，被广泛应用于实际问题中。

通过对其工作原理的深入理解，可以帮助我们更好地应用该算法，从而实现对实际问题的分类和预测。

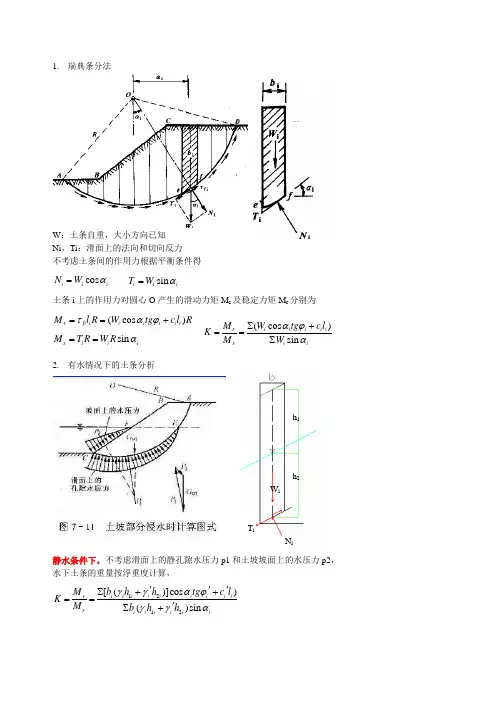
1212[()]cos )()sin i i i i i i i i i r s i i i i i i b h h tg c l M K M b h h γγαϕγγα'''∑++=='∑+(cos )r fi i i i i i i M l R W tg c l R ταϕ==+(cos )sin i i i i i r s i i W tg c l M K M W αϕα∑+==∑sin i i i T W α=cos ii i N W α=sin s i i i M T R W R α==1. 瑞典条分法W ：土条自重，大小方向已知 Ni ，Ti ：滑面上的法向和切向反力不考虑土条间的作用力根据平衡条件得土条i 上的作用力对圆心O 产生的滑动力矩M s 及稳定力矩M r 分别为2. 有水情况下的土条分析静水条件下，不考虑滑面上的静孔隙水压力p1和土坡坡面上的水压力p2， 水下土条的重量按浮重度计算，h 1W ih 2T iN isin i α=123123[()]cos )()sin i i i i i i i i i i i r s i i i sati i i i i b h h h tg c l M K M b h h h γγγαϕγγγα''''∑+++=='∑++2sin i w i iJ b h γα=∑['(cos )tan ']sin i i i i i i i s i i c l W u L F W αϕα+-=∑∑由荷载引起的超静孔隙水压力条件下（有效应力法） 当有超静孔隙水压力时，超静孔隙水压力作用在滑面上， 减小土条的有效法向应力由渗流引起的超静孔隙水压力条件下（代替法）流线平行坡面时， 用浸润线以下，坡外水位以上 所包围的同体积的水重对滑动圆心的力矩代替渗流力对 圆心的滑动力矩。

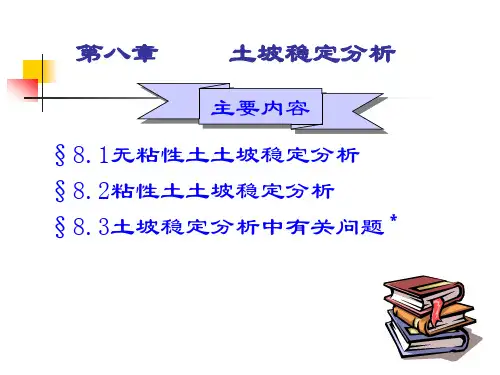
毕肖普条分法毕肖普条分法是一种常用的论证方法，它由英国哲学家毕肖普（Isaac Newton）提出，被广泛应用于各个领域的论述和思考中。

其核心思想是将一个复杂的问题或概念分解成若干个简单的部分，以便更好地理解和分析。

本文将从以下几个方面详细介绍毕肖普条分法。

一、毕肖普条分法的基本原理毕肖普条分法是一种归纳推理方法，其基本原理是将一个复杂的问题或概念分解成若干个简单的部分，以便更好地理解和分析。

具体而言，毕肖普条分法包括以下三个步骤：1. 将问题或概念拆解成若干个部分。

2. 对每个部分进行独立思考和讨论。

3. 将各部分综合起来得出总结性结论。

二、毕肖普条分法的应用场景毕肖普条分法可以应用于各种不同领域的论述和思考中。

以下列举几个常见的应用场景：1. 学术研究：在学术研究中，毕肖普条分法可以用来分析和解决复杂的理论问题。

例如，对于一个复杂的学术概念，可以将其拆分成若干个部分进行独立思考和讨论，最终得出总结性结论。

2. 商业决策：在商业决策中，毕肖普条分法可以用来分析和解决复杂的市场问题。

例如，对于一个新产品的市场推广计划，可以将其拆分成若干个部分进行独立思考和讨论，最终得出总结性结论。

3. 政策制定：在政策制定中，毕肖普条分法可以用来分析和解决复杂的社会问题。

例如，对于一个社会改革计划，可以将其拆分成若干个部分进行独立思考和讨论，最终得出总结性结论。

三、毕肖普条分法的优点毕肖普条分法有以下几个优点：1. 使问题更易理解：通过将一个复杂的问题或概念拆解成若干个简单的部分进行独立思考和讨论，在整体上使问题更易理解。

2. 便于深入探究：通过对每个部分进行独立思考和讨论，可以更深入地探究问题的本质和细节。

3. 有利于综合分析：通过将各部分综合起来得出总结性结论，可以更全面地分析问题并得出更准确的结论。

四、毕肖普条分法的局限性毕肖普条分法也存在一些局限性：1. 不适用于所有问题：毕肖普条分法适用于那些可以拆解成若干个简单的部分进行独立思考和讨论的问题，对于那些本身就比较简单或难以拆解的问题，该方法并不适用。

.1. 不考虑浸水条件某路堤 H =13.0m，堤顶宽 B=10.0m，拟定横断面见图 1. 试1验得知：土的干重度3，孔隙率=31%，10 。

干 =18.13KN/m=26 ，c1=14.7KPa，换算土柱高h0=1.0m。

试计算其边坡稳定性。

解：按条分法的步骤如下：（1）按 1:50 比例作图，用 4.5H 法作圆心辅助线，定圆心O1划分九个土条；（2）分别量取各土条重心与竖轴的间距a i（右正左负），计算 a；量面积 F i，分别计算重力Q i；（3）量滑动圆弧两端点对竖轴的间距，计算圆心角0 和全弧长 L；（4）分别计算各土条圆弧面上的法向力N i和切向力 T i（区分正负）；以上所有计算结果列于表 1 中。

（5）按以上方法定圆心O2，O3，O4，O5，划分土条，对其相应数据进行计算，分别列于表2,3,4,5中。

（6）计算动水压力 D I * *F2（7） f 1=tan1=0.4877,（8）计算 K=NifxcLi，计算结果列于图表中。

T i（9）绘 K 值曲线，确定K min=0.78. 边坡稳定性满足要求。

.2.考虑浸水条件某浸水路堤 H =13.0m，堤顶宽 B=10.0m，拟定横断面见图 1. 试1验得知：土的重度325.48KN / m3干重度干=18.13KN/m，孔隙率0。

0=31%，1 =26 ，2 =22 ， c1=14.7KPa， c2=7.84KPa, 换算土柱高h0=1.0m。

试计算其边坡稳定性。

解：按条分法的步骤如下：（10）按 1:50 比例作图，用 4.5H 法作圆心辅助线，定圆心O1划分九个土条；（11）分别量取各土条重心与竖轴的间距a i（右正左负），计算 a；量面积 F i，分别计算重力Q i；其中湿重度w(0 )(1)=（25.48-9.80）（1-0.31）=10.82KN/m3（12）量滑动圆弧两端点对竖轴的间距，计算圆心角0 和全弧长 L；（13）分别计算各土条圆弧面上的法向力N i和切向力 T（i区分正负）；以上所有计算结果列于表 1 中。

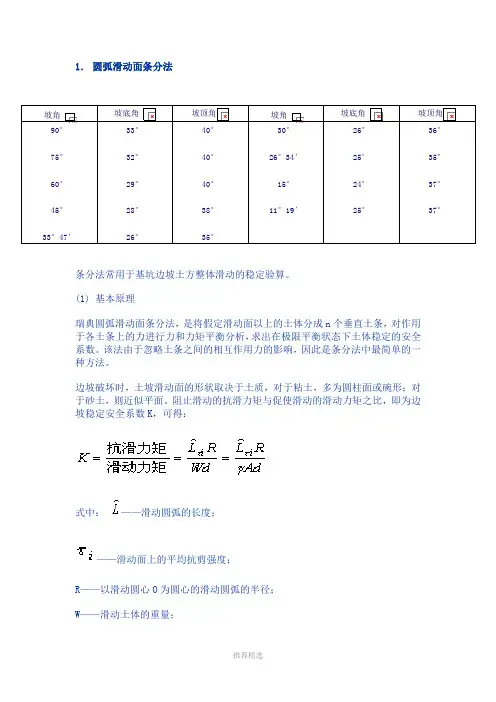
1． 圆弧滑动面条分法条分法常用于基坑边坡土方整体滑动的稳定验算。

(1) 基本原理瑞典圆弧滑动面条分法，是将假定滑动面以上的土体分成n 个垂直土条，对作用于各土条上的力进行力和力矩平衡分析，求出在极限平衡状态下土体稳定的安全系数。

该法由于忽略土条之间的相互作用力的影响，因此是条分法中最简单的一种方法。

边坡破坏时，土坡滑动面的形状取决于土质，对于粘土，多为圆柱面或碗形；对于砂土，则近似平面。

阻止滑动的抗滑力矩与促使滑动的滑动力矩之比，即为边坡稳定安全系数K ，可得：式中： ——滑动圆弧的长度；——滑动面上的平均抗剪强度；R ——以滑动圆心O 为圆心的滑动圆弧的半径； W ——滑动土体的重量；坡角坡底角坡顶角坡角坡底角坡顶角90° 75° 60° 45°33°47′33° 32° 29° 28° 26°40° 40° 40° 38° 35°30°26°34′ 15° 11°19′26° 25° 24° 25°36° 35° 37° 37°d——W作用线对滑动圆心O的距离；A——滑动面积。

如K>1.0表示边坡稳定；K=1.0边坡处于极限平衡状态；K<1.0则边坡不稳定。

按上述原理进行计算，首先要确定最危险滑动圆弧的形状，即首先要找出最危险滑动圆弧的滑动圆心O，然后找坡角圆即可画出最危险滑动圆弧。

欲找出K值最小的最危险滑动圆弧，可根据不同的土质采用不同的方法：a.内摩擦角的高塑性粘土这种土的最危险滑动圆弧为坡脚圆，可按下述步骤求其最危险滑动圆弧的滑动圆心。

(a) 由此表，根据坡角查出坡底角和坡顶角。

(b) 在坡底和坡顶分别画出坡底角和坡顶角，两线的交点O，即最危险滑动圆弧的滑动圆心。

基本法23条的理解
1.基本法23条的内容概述
基本法23条分为两款，第一款规定了香港特别行政区应自行立法禁止七种危害国家安全的罪行，包括分裂国家、颠覆国家政权、恐怖活动等。

第二款明确了中央人民政府在香港特别行政区设立的机构，如国家安全委员会等。

2.基本法23条的立法过程和意义
基本法23条的立法过程反映了我国政府对香港特别行政区的关爱和支持。

从起草、审议到通过，每一步都充分体现了民主、法治和一国两制的原则。

基本法23条的实施，有助于维护国家主权、安全和发展利益，保持香港长期繁荣稳定。

3.基本法23条在我国法律体系中的地位
基本法23条是我国法律体系中关于特别行政区立法的重要条款，具有权威性和指导性。

它既保证了国家主权和安全，又兼顾了香港特别行政区的特色和需要。

4.基本法23条的具体实施和影响
基本法23条的实施，对香港特别行政区具有重要意义。

它有助于完善香港特别行政区的法律体系，强化国家安全保障，有利于香港社会的稳定和发展。

同时，它也对其他特别行政区的法律制度具有借鉴意义。

5.结论：基本法23条的重要性和实践价值
总之，基本法23条作为我国法律体系的重要组成部分，既彰显了国家对香港特别行政区的关爱，又为香港的繁荣稳定提供了有力的法治保障。

只有全
面准确地理解和实施基本法23条，才能确保香港特别行政区的长治久安。

２０１４年第３期　（总第２４１期）　黑龙江交通科技　ＨＥＩＬＯＮＧＪＩＡＮＧ　ＪｌＡＯＴＯＮＧ　ＫＥＪ　Ｎｏ．３，２０１４　（Ｓｕｍ　Ｎｏ．２４１）　

条分法的表解和图解　杨兴杰　（河北路桥集团有限公司）　

摘要：介绍了条分法的表解法和图解法。　关键词：条分法；表解；图解　中图分类号：Ｕ４１６．１　文献标识码：Ｃ　文章编号：１００８—３３８３（２０１４）０３—００３９—０１　

条分法计算工作量较大，可以简化为表解法和图解法，　供工程设计粗略估算使用。此方法不计行车荷载，圆心位置　用３６。法确定，稳定系数适当增大。　１表解法　如图１所示，将土条的高度ａ、宽度ｂ及弧长　，统一换　算成边坡高度日的函数，即　＝ＹＨ，ｂ＝ＸＨ，Ｌ＝ＺＨ，则１　

Ｋ＝ｆ。Ａ　Ｃ・Ｂ　（１）　

式中：Ａ和　为换算系数，其值与　、ｙ及ｚ有关，即　２ＸＹｃｏｓａｆ　ｎ　Ｚ　Ａ　—ＺＸＹ—ｓｉｎａｌ　、、　Ｊ　Ｉ　Ｊ　Ｉ　图１表解法计算图式　Ａ与曰值随路基边坡坡度而变，如表１所列。　表１边坡稳定验算的Ａ和Ｂ值表　例１已知某土坡妒＝２２。，ｃ＝９．８　ｋＰａ，　＝１６．６６　ｋＮ／ｍ　，　ｍ＝１．５，Ｈ＝１０．０　ｍ，试计算边坡稳定性。　解依ｍ＝１．５，查表得五个圆心的Ａ与Ｂ值，ｆ＝　２。＿ｏ．４ｏ４，南＿０・ｏ５９。　由式（９）的计算结果见表２，其中Ｋｍ。　＝１．２６。　收稿日期：２０１３—１２—１１　表２表解法计算结果表　稳定系数　大于１．２５，该边坡稳定。　表解法为近似解，Ｋ值要求应略为提高，例如要求　；　≥１．５，则上述算例的边坡为不稳定。此时可假定　值，　利用表解法反求边坡率ｍ值或边坡高日值。例如取Ｋ＝　１．５，ｍ取１．５，其他条件与例１相同。如取Ａ＝１．９Ｏ，Ｂ＝　８．３３，反算得Ｈ＝６．７　ｍ。同样条件下，也可以取Ｈ＝１０．０　ｍ，按　例１计算步骤，假定坡率，直到　≥１．５为止。　２图解法　圆弧滑动面的图解法有多种，其中之一是取Ｋ＝１．０（极