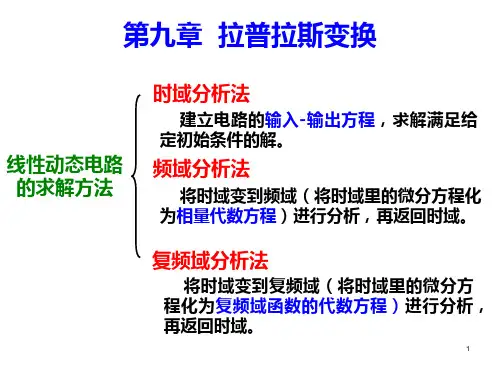
第九章_拉普拉氏变换(二)
- 格式:ppt
- 大小:795.50 KB
- 文档页数:22







拉氏变换什么是拉氏变换拉氏变换(Laplace Transform)是一种将函数从时间域转换到复频域的数学工具。
它在工程学科和物理学中有广泛的应用,特别是在控制系统分析和信号处理领域。
拉氏变换通过积分运算将一个函数从时间域(t-domain)变换到频域(s-domain),其中s是一个复变量。
拉氏变换的定义给定一个函数f(t),其拉氏变换F(s)定义为:F(s) = L{f(t)} = ∫[0, ∞] e^(-st) f(t) dt这里,s是复变量,e是自然对数的底数,t表示时间。
拉氏变换的性质拉氏变换具有许多有用的性质,以下是一些常见的性质:1.线性性质:L{af(t) + bg(t)} = aF(s) + bG(s),其中a和b是常数。
2.移位性质:L{f(t - a)} = e^(-as)F(s),其中a是常数。
3.初值定理:lim_[s→∞] sF(s) = f(0),其中f(0)是函数f(t)在t=0时的初值。
4.终值定理:lim_[s→0] sF(s) = lim_[t→∞] f(t),即函数f(t)在t→∞时的极限等于F(s)在s=0时的极限。
这些性质使得拉氏变换成为了解决微分方程问题以及计算复杂电路的有效工具。
拉氏变换的应用1. 信号处理在信号处理领域,拉氏变换用于分析和处理连续时间信号。
通过将信号从时间域转换到频域,可以更好地理解信号的频谱特性,并进行滤波、降噪、调制等处理。
2. 控制系统在控制系统分析中,拉氏变换被广泛用于研究和设计控制系统的性能和稳定性。
通过将控制系统表示为拉氏域的传输函数,可以方便地进行频率响应、稳定性分析和控制器设计。
3. 电路分析在电路分析中,拉氏变换用于求解电路的幅频特性、相频特性和传输函数。
通过将电路中的电压和电流转换到拉氏域,可以更方便地进行复杂电路的分析和计算。
4. 信号传输拉氏变换在信号传输中的应用非常广泛。
信号的拉氏变换可以帮助我们理解信号在传输过程中的衰减、失真和干扰等问题,从而优化信号传输的方案。


拉普拉氏变换的数学公式1. 什么是拉普拉氏变换?大家好,今天我们要聊聊拉普拉氏变换。
乍一听,这名字是不是有点高深莫测?其实,它在数学里可是个非常实用的工具。
简单来说,拉普拉氏变换就是把一个函数从时间域“变身”为复频域的一个过程。
这就像把一道难题换成了另一种形式,更容易解决。
2. 拉普拉氏变换的基本公式要搞清楚拉普拉氏变换,首先得了解它的基本公式。
这个公式有点像一条魔法公式,让复杂的函数变得简单。
公式长这样:[ mathcal{L}{f(t)} = F(s) = int_{0}^{infty} e^{st} f(t) , dt ]。
看起来是不是有点复杂?别急,让我们慢慢拆解。
2.1 公式的组成部分(mathcal{L}{f(t)}):这个符号代表拉普拉氏变换,意思就是我们要对函数 (f(t)) 进行变换。
(F(s)):这就是变换后的结果,换句话说,就是 (f(t)) 在复频域的表现。
(int_{0}^{infty} e^{st} f(t) , dt):这是公式的核心部分,表示我们对函数 (f(t)) 和(e^{st}) 的乘积进行积分。
这里的 (s) 是一个复数变量,通常包括实部和虚部。
2.2 如何理解公式?这个公式可以分成两部分来看。
首先,我们用 (e^{st}) 这个“加速器”来调整函数(f(t)) 的形态。
然后,通过积分的方式,把调整后的函数从 (t) 这个时间域转化到 (s) 这个复频域。
听起来是不是有点像魔法?其实这就是数学的奇妙之处。
3. 拉普拉氏变换的应用了解了公式,我们接下来看看这个变换在实际中有什么用处。
3.1 解决微分方程拉普拉氏变换在解决微分方程上可是大显身手。
你可以把它当作一个神器,能将微分方程转化为代数方程,这样解决起来简单多了。
就好像你原本在看一篇英文小说,突然有了一个翻译器,瞬间变得清晰明了。
3.2 电路分析如果你对电路感兴趣,拉普拉氏变换也是个好帮手。
在分析电路的时候,我们经常会遇到一些复杂的电路方程。