下载文档原格式
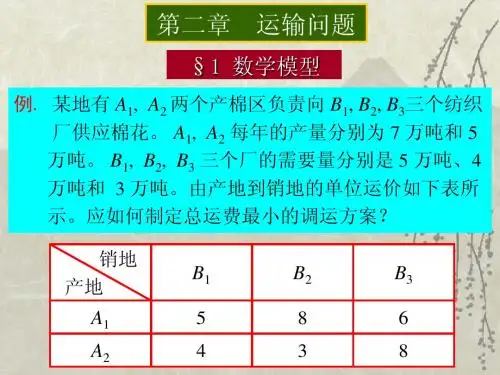
第二次 运输问题1．运输问题的一般提法设有m 个产地m A A A ,,,21 ，将生产的物资联合运往n 个销地n B B B ,,,21 ；各产地i A 的产量为i a ，各销地j B 的销量为j b ；从i A 产地到j B 销地的单位运价为j i c ，问如何组织运输，可使总的运费最少？如果总的产量=∑=mi i a 1总的销量∑=nj j b 1，则称它为产销平衡运输问题2．产销平衡运输问题的数学模型引入决策变量：用j i x 表示从i A 产地运到j B 销地的物资数量确定目标函数：使总运输费用最少 ∑∑===mi nj j i j i x c Z 11m i n写出约束条件：从i A 产地运出的物资数量应等于i A 产地的物资供应量 即i nj ji a x=∑=1m i ,,2,1 =运到j B 销地的物资数量应等于j B 销地的需求量 即j mi ji b x=∑=1n j ,,2,1 =j i x 取值非负。
说明：① 运输问题是一线性规划问题；② db a x j i j i ⋅=（其中∑∑====nj j m i i b a d 11）是运输问题的一个可行解，从而它有基本可行解；又{}j i j i b a x ,min ≤，故运输问题的任一可行解都是有限的，即可行域有界；因此运输 问题必有有限最优解且最优解同样可在基本可行解处得到。
③ 针对m 个产地n 个销地的产销平衡运输问题，其约束条件中共有n m +个方程，但这 n m +个方程中，任一方程都可以通过其余1-+n m 方程得到。
因此真正有效的方程个数是1-+n m 个，我们可以将多余的一个方程划掉。
这样以来，运输问题的基本可行解中只含1-+n m 个基变量。
④ 当m 和n 取值较大时，引入的决策变量较多，采用表格单纯形法计算量较大，通常采用 表上作业法求解运输问题。
3．求初始调运方案（初始基本可行解）1）左上角方法：从表格中左上角方格所对应的决策变量开始分配运输量，分配时让它取尽可能大的取值。
南邮运筹学运输问题实验报告南邮运筹学运输问题实验报告1.实验目的：本次实验旨在通过针对不同运输问题的建模和解决过程，掌握运筹学在实际运输问题中的应用方法，提高运筹学实践能力。
2.实验内容：本次实验包括两个部分：单源最短路径问题和车辆路径规划问题。
（1）单源最短路径问题：通过建立带权有向图模型，使用Dijkstra算法和Bellman-Ford算法求解从起点到终点的最短路径及其长度。
（2）车辆路径规划问题：通过建立车辆路径规划模型，使用模拟退火算法和遗传算法求解最短路径和最短时间路径。
3.实验结果：（1）单源最短路径问题：使用Dijkstra算法求解起点到终点的最短路径和长度如下图所示：路径：1->3->4->5->7，路径长度为23。
使用Bellman-Ford算法求解起点到终点的最短路径和长度如下图所示：路径：1->3->4->5->7，路径长度为23。
（2）车辆路径规划问题：使用模拟退火算法求解最短路径和最短时间路径如下图所示：最短路径：1->4->5->2->3->1，路径长度为33；最短时间路径：1->3->4->5->2->1，路径时间为15。
使用遗传算法求解最短路径和最短时间路径如下图所示：最短路径：1->4->5->2->3->1，路径长度为33；最短时间路径：1->3->4->5->2->1，路径时间为15。
4.实验结论：本次实验通过求解单源最短路径问题和车辆路径规划问题，掌握了Dijkstra算法、Bellman-Ford算法、模拟退火算法和遗传算法等运筹学方法在实际运输问题中的应用，提高了运筹学实践能力。
5.反思与改进：在实验过程中，我们发现需求和条件的准确描述很重要。
在建模过程中，不光需要理解题目中提供的条件，还需要利用常识和实际情况对模型进行适当的修正和完善。
课内实验报告课程名：运筹学任课教师：邢光军专业：学号：姓名：/ 学年第学期南京邮电大学管理学院售，各工厂的生产量、各销售中心的销售量（假定单位均为吨）、各工厂到各销售点的单位运价（元/吨）示于表1中。
要求研究产品如何调运才能使总运费最小。
表1 产销平衡表和单位运价表实验结果：一：问题分析和建立模型：解：由于总产量（7+4+9=20）=总销量（3+6+5+6=20），故该问题为产销平衡问题。
其数学模型如下：设从Ai运往Bi的运量为Xij，（i =1,2,3，j=1,2,3,4）Min Z=3X11+11X12+3X13+10X14+X21+9X22+2X23+8X24+7X31+4X32+10X33+5X34s.t. X11+X12+X13+X14=7X21+X22+X23+X24=4X31+X32+X33+X34=9X11+X21+X31=3X12+X22+X32=6X13+X23+X33=5X14+X24+X34=6Xij>=0,i=1,2,3;j=1,2,3,4二：计算过程：与一般的线性规划问题的解法类似，首先需要建立运输问题的电子表格。
下面利用Spreadsheet来求解该问题：在Excel2003版本中，单击“工具”栏中“加载宏”命令，在弹出的的“加载宏”对话框选择“规划求解”，在“工具”下拉菜单中会增加“规划求解”命令，这样就可以使用了。
1、将求解模型及数据输入至Spreadsheet工作表中。
在工作表中的B3~F3单元格分别输入单位运价,销地B1,销地B2,销地B3,销地B4,B4~B6单元格分别输入产地A1,产地A2,产地A3,C4~F6单元格分别输入价值系数（单位运价）。
在工作表中的B8~G8，G10单元格分别输入运输量,销地B1,销地B2,销地B3,销地B4,实际产量，产量。
B9~B13单元格分别输入产地A1,产地A2,产地A3,实际销量，销量。
C4~F6单元格分别表示矩阵决策变量的取值。
实验报告填写说明
（实验项目名称、实验项目类型必须与实验教学大纲保持一致）
1．实验环境：
实验用的硬件、软件环境。
2．实验目的：
根据实验教学大纲，写出实验的要求和目的。
3．实验原理：
简要说明本实验项目所涉及的理论知识。
4．实验步骤：
这是实验报告极其重要的容。
对于验证性验，要写清楚操作方法，需要经过哪几个步骤来实现其操作。
对于设计性和综合性实验，还应写出设计思路和设计方法。
对于创新性实验，还应注明其创新点。
5．实验结论：
根据实验过程中得到的结果，做出结论。
6．实验总结：
本次实验的收获、体会和建议。
7．指导教师评语及成绩：
指导教师依据学生的实际报告内容，给出本次实验报告的评价和成绩。
附录1：源程序。
南邮运筹学实验2
课内实验报告
课程名：运筹学
任课教师：朱京辉
2014 /2015 学年第 2 学期南京邮电大学管理学院
根据产销平衡建立约束条
minZ=3x11+11x12+3x13+10x14+x21+9x22+2x23+8x24+7x31+4x32+10x33+5x34 x11+x12+x13+x14=7
x21+x22+x23+x24=4
x31+x32+x33+x34=9
x11+x12+x13=3
x21+x22+x23=6
x31+x32+x33=5
x41+x42+x43=6
x ij≥0，（i=1,2,3，j=1,2,3,4）
结果分析
1.先将约束条件填写进表格
2.计算实际产量
3.计算实际销量
4.计算总费用
5.约束条件
6.结果
x13=5, x14=2,x21=3,x24=1,x32=6,x34=3,总费用为85
成绩评定：
该生对待本次实验的态度□认真□良好□一般□比较差。
本次实验的过程情况□很好□较好□一般□比较差
对实验结果的分析□很好□良好□一般□比较差
文档书写符合规范程度□很好□良好□一般□比较差
综合意见：
成绩指导教师签
名
日期。
南邮课内实验-运筹学-运输问题-第二次
课内实验报告
课程名：运筹学
任课教师：邢光军
专业：
学号：
姓名：
/ 学年第学期
南京邮电大学管理学院
实验背景：某企业集团有3个生产同类产品的工厂，生产的产品由4
个销
售中心出售，各工厂的生产量、各销售中心的销售量（假定单位均为吨）、各工厂到各销售点的单位运价（元/吨）示于表1中。
要求研究产品如何调运才能使总运费最小。
表1 产销平衡表和单位运价表
实验结果：
一：问题分析和建立模型：
解：由于总产量（7+4+9=20）=总销量（3+6+5+6=20），故该问题为产销平衡问题。
其数学模型如下：
设从Ai运往Bi的运量为Xij，（i =1,2,3，j=1,2,3,4）
Min Z=3X11+11X12+3X13+10X14+X21+9X22+2X23+8X24+7X31+4X32+10X33+5X34
s.t. X11+X12+X13+X14=7
X21+X22+X23+X24=4
X31+X32+X33+X34=9
X11+X21+X31=3
X12+X22+X32=6
X13+X23+X33=5
X14+X24+X34=6
Xij>=0,i=1,2,3;j=1,2,3,4
二：计算过程：
与一般的线性规划问题的解法类似，首先需要建立运输问题的电子表格。
下面利用Spreadsheet来求解该问题：
在Excel2003版本中，单击“工具”栏中“加载宏”命令，在弹出的的“加载宏”对话框选择“规划求解”，在“工具”下拉菜单中会增加“规划求解”命令，这样就可以使用了。
1、将求解模型及数据输入至Spreadsheet工作表中。
在工作表中的B3~F3单元格分别输入单位运价,销地B1,销地B2,销地B3,销地B4,B4~B6单元格分别输入产地A1,产地A2,产地A3,C4~F6单元格分别输入价值系数（单位运价）。
在工作表中的B8~G8，G10单元格分别输入运输量,销地B1,销地B2,销地
B3,销地B4,实际产量，产量。
B9~B13单元格分别输入产地A1,产地A2,产地A3,实际销量，销量。
C4~F6单元格分别表示矩阵决策变量的取值。
C13~F13（销量），I9~I11（产量）单元格值为约束1~7不等式符号左边部分，如I9=SUM（C9：
F9），,其余C13~F13,I10~I11含义雷同。
C12~F12(实际销量)，G9~G11（实际产量）单元格数据为约束1~7不等式符号右端系数。
I13单元格表示目标函数（总费用）取值（=SUMPRODUCT(C4：F6，C9：F11)）。
2、单击“工具”菜单中的“规划求解”命令，弹出“规划求解参数”对话框。
在“规划求解参数”对话框中设置目标单元格为I13，选中“最小值”前的单选按钮，设置可变单元格为C9：F11。
单击“规划求解参数”对话框中的“添加”按钮，打开“添加约束”对话框，单击单元格引用位置文本框，然后选定工作表的C13~F13单元格，则在文本框中显示“$C$13~$F$13”,选择“=”的约束条件，在约束值文本框中输入C12~F12单元格，则在文本框中显示
“$C$12~$F$12”。
单击“添加”按钮，把所有的约束条件都添加到“规划求解参数”对话框的“约束”列表框中。
其余1条约束不等式的输入方法雷同。
按照同样的方法继续输入决策变量的非负约束、整数约束。
（如图 ）
图①
3、在“规划求解参数”对话框中单击“求解”按钮，弹出“规划求解结果”对话框，选中“保存规划求解结果”前的单选按钮，单击“确定”按钮，工作表中就显示规划求解的结果。
（如图②）
图②
三：结果分析：
B1 B2 B3 B4
A1 5 2
A2 3 1
A3 6 3
四：实验心得：
本次实验我们求解的是运输问题，我借助了上次运用EXCEL求解线性规划问题的经验，比上次更加快速、准确地得到了运输问题的答案。
然而我在本次求解中发现我用EXCEL求解得出的运输问题的答案与讲义上给出的答案不一致，虽然结果均为85，但是有几个决策变量的取值不同。
并且我求算了几遍都是那个结果。
后来经过邢老师的讲解，我才知道原来EXCEL求算时可能会产生不同的最优解，只要目标函数值一样，那么我所求得的解就是另一个最优解，也同样正确。
