现代控制理论MATLAB编程

现代控制理论基于MATLAB的实验指导书第一部分实验要求1．实验前做好预习。

2．严格按照要求操作实验仪器，用毕恢复原状。

3．实验完成后，由指导教师检查实验记录、验收仪器后，方可离开。

4．实验报告应包括以下内容：1）实验目的；2）实验原理图；3）实验内容、步骤；4）仿真实验结果（保留仿真实验波形，读取关键参数）；5）仿真实验结果分析。

第二部分MATLAB平台介绍实际生产过程中，大部分的系统是比较复杂的，并且要考虑安全性、经济性以及进行实验研究的可能性等，这在现场实验中往往不易做到，甚至根本不允许这样做。

这时，就需要把实际系统建立成物理模型或数学模型进行研究，然后把对模型实验研究的结果应用到实际系统中去，这种方法就叫做模拟仿真研究，简称仿真。

到目前为止，已形成了许多各具特色的仿真语言。

其中美国Mathworks软件公司的动态仿真集成软件Simulink与该公司著名的MATLAB软件集成在一起，成为当今最具影响力的控制系统应用软件。

国内MA TLAB软件的著名论坛为“MATLAB中文论坛”，网址为：https:///forum.php，建议同学们注册并参与论坛相关内容的讨论。

图1 MA TLAB仿真环境第三部分 实验实验一线性系统的时域分析实验目的熟悉MATLAB 环境，掌握用MATLAB 控制系统工具箱进行线性定常系统的时域分析、能控性与能观性分析、稳定性分析的方法。

实验要求完成指导书规定的实验内容，记录并分析实验结果，写出实验报告。

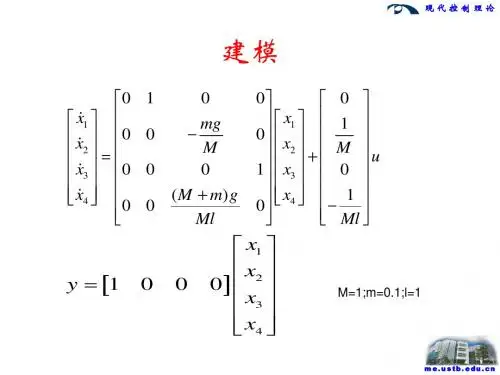
实验内容1．已知系统的状态模型，求系统在单位阶跃输入下的各状态变量、输出响应曲线。

例：[]⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡2121214493.69691.1,0107814.07814.05572.0x x y u x x x x 。

键入：a = [-0.5572, -0.7814; 0.7814,0]; b = [1; 0]; c = [1.9691,6.4493]; d = 0;[y, x, t]=step(a, b, c, d); plot(t, y); grid （回车，显示输出响应曲线。

现代控制理论的MATLAB实现现代控制理论是控制工程中一门重要的学科，它研究如何设计和分析控制系统以满足一定的性能指标。

MATLAB是一种功能强大的科学计算和工程仿真软件，广泛应用于控制系统设计与分析。

本文将介绍现代控制理论的一些常见方法在MATLAB中的实现。

1.线性系统的状态空间表示线性系统的状态空间表示是现代控制理论的核心内容之一、在MATLAB中，可以使用`ss`命令创建线性系统的状态空间模型。

例如，假设存在一个二阶线性时不变系统，其传递函数为：可以使用以下代码将其转换为状态空间模型：```matlabnum = [1];den = [1, 1, 1];sys = tf(num, den);ss_sys = ss(sys);```2.线性系统的传递函数表示传递函数是描述线性系统输入输出关系的一种常用表示方法。

在MATLAB中，可以使用`tf`命令创建线性系统的传递函数模型。

例如，假设存在一个二阶线性时不变系统，其状态空间描述为：```matlabA=[0,1;-1,-1];B=[0;1];C=[1,0];D=0;ss_sys = ss(A, B, C, D);```可以使用以下代码将其转换为传递函数模型：```matlabtf_sys = tf(ss_sys);```3.常见控制器的设计与分析现代控制理论中常用的控制器设计方法包括PID控制器、根轨迹法、频率域分析等。

在MATLAB中，可以使用`pid`命令创建PID控制器，并使用`rlocus`命令绘制根轨迹图。

例如，创建一个PID控制器：```matlabKp=1;Kd=0.1;pid_controller = pid(Kp, Ki, Kd);```绘制根轨迹图：```matlabsys = tf([1], [1, 1, 1]);rlocus(sys);```4.系统的频率响应分析频率响应分析是现代控制理论中常用的系统性能评估方法之一、在MATLAB中，可以使用`bode`命令绘制系统的频率响应曲线。

现代控制原理matlab实验报告实验一.利用MATLAB进行线性系统的模型转换及联结一．实验目的1、学习系统状态空间模型的建立方法、了解状态空间模型与传递函数、零极点模型之间相互转换的方法；2、通过编程、上机调试，掌握系统状态空间模型与传递函数相互转换的方法。

3、通过编程、上机调试，掌握系统模型的联结方法。

二．实验步骤1、根据所给系统的已知条件，如传递函数、零极点模型或（A 、B 、C 、D ），实现状态空间模型、传递函数模型、零极点增益模型之间的转换，采用MATLAB 的相关函数编写m -文件。

2、应用系统建模工具，并联、串联、闭环、反馈等函数解决实际问题。

3、在MA TLAB 界面下调试程序。

三．实验要求1．在运行以上例程序的基础上，应用MA TLAB 求下面传递函数阵的状态空间实现232252()234s s s G s s s s +⎡⎤⎢⎥++⎣⎦=+++提示：num =[0 0 1 2；0 1 5 3] 解：num=[0 0 1 2;0 1 5 2]; den=[1 2 3 4];[A,B,C,D]=tf2ss(num,den) A =-2 -3 -4 1 0 0 0 1 0 B =1 0 0 C =0 1 2 1 5 2 D =0 02．一个双输入双输出系统112233412311022711353x x x x u x x -⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦⎣⎦11223120011x y x y x ⎡⎤⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎣⎦求出此模型的能控标准型和能观标准型。

提示：写出两个子系统的传递函数模型，进而求出这两个传递函数模型的能控标准型实现或能观标准型实现，讨论是否能通过子系统的能控标准型实现或能观标准型实现求出原来系统的能控标准型和能观标准型。

解：A=[4 1 -2;1 0 2;1 -1 3]; B=[3 1;2 7;5 3]; C=[1 2 0;0 1 1]; D=[0];[num1,den1]=ss2tf(A,B1,C1,D) [num2,den2]=ss2tf(A,B2,C2,D)得到： num1 =0 7.0000 -19.0000 -36.0000den1 =1.0000 -7.0000 15.0000 -9.0000num2 =0 10.0000 -60.0000 98.0000den2 =1.0000 -7.0000 15.0000 -9.0000实验二.利用MATLAB 求取线性系统的状态空间模型的解并分析其稳定性一. 实验目的1、根据状态空间模型分析系统由初始状态和外部激励所引起的响应；2、了解系统稳定性的判定方法（直接法和间接法）；3、通过编程、上机调试，掌握系统运动的分析方法。

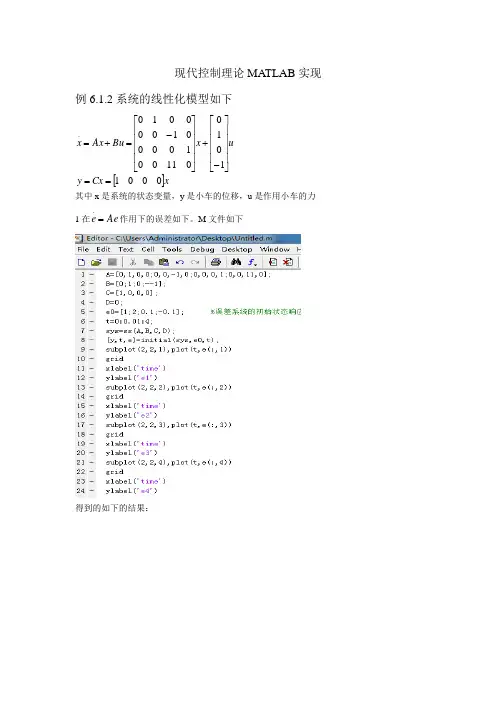
现代控制理论MATLAB 实现例6.1.2系统的线性化模型如下[]xCx y ux Bu Ax x 0001101001100100001000010.==⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=+=其中x 是系统的状态变量，y 是小车的位移，u 是作用小车的力 1在Ae e =.作用下的误差如下。

M 文件如下得到的如下的结果：设计一个状态观测器，使得观测器极点是10,10,322,3224321-=-=+-=+-=u u j u j u解 观测器模型如下Ly Bu x LC A x++-=~.)(~运行如下m 文件状态估计的误差状态方程为：e LC A e )(.-=以下进一步通过仿真来检验观测器的效果，取初始误差向量为[]Te 1.01.021)0(-=执行如下m 文件状态估计的误差曲线如下降维观测器的题：例6,3,2考虑系统Cxy Bu Ax x =+=.其中，[]001,100,6116100010=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=C B A 设计一个具有极点u1=-10,u2=-10,的降维的观测器。

因此降阶观测器的增益矩阵是L=[]T514,具有期望极点的降阶观测器为u y w w ⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--+⎥⎦⎤⎢⎣⎡---=10260191616114~.~跟踪控制器的设计例5.4.1已知被控对象的状态空间模型为[]xy u x x 21104310.=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--= 设计状态反馈控制器，使得闭环极点为-4和-5，和跟踪控制器。

并讨论闭环系统的稳态性能。

可以知道能稳定跟踪先判断是否能稳定跟踪可以得到如下的结果00.511.522.530.20.40.60.811.21.4time(sec)O u t p u t最优控制的习题例7.2.2考虑以下状态空间模型的描述的系统：其中⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=100,92735100010B A系统的性能指标J 定义为 ⎰∞+=)(t T T d Ru u Qx x J其中，[]1,100010001=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=R Q 设计最优状态反馈控制器，并检验最优闭环系统对初始状态[]Tx 001)0(=的响应。

现代控制理论实验报告姓名：班级:学号：目录一．实验设备二．实验目的三．实验步骤一、实验设备PC计算机1台,MATLAB软件1套。

二、实验目的1。

学习系统状态空间表达式的建立方法、了解系统状态空间表达式与传递函数相互转换的方法；2。

通过编程、上机调试、掌握系统状态空间表达式与传递函数相互转换方法;3。

学习MATLAB的使用方法。

三、实验步骤1、根据所给系统的结构图写出死循环系统的传递函数，若K=10，T=0。

1时阶跃输出下的系统输出响应,并采用MATLAB编程.2、在MATLAB接口下调试程序，并检查是否运行正确.3、给出定二阶系统结构图:图为二阶系统结构图（1）求二阶系统的闭环循环传递函数ɸ(s ）=)(1)(s G s G +=K S TS K++2（2)若K=10，T=0。

1，仿真给出阶跃下的系统输出响应把K T 代入方程得Φ（S)= =1）MATLAB 命令得出的系统响应曲线在MATLAB 上输入下列指令：〉> num=［100]；>> den=［1，10，100]；>> step （num,den)程序运行后显示的时域动态响应曲线（如图2)图为 时域动态响应曲线2）、用进行Simulink 进行仿真启动Simulink并打开一个空白的模块编辑窗口,画出所需模块,并给出正确参数，将画出的所有模块链接起来（如图1）,构成一个原系统的框图描述(如图3）.选择仿真控制参数，启动仿真过程。

仿真结果示波器显示如图4。

图3二阶系统的Simulink(仿真）图4仿真结果示波器显示（仿真输出）（3) 调整比例系数K，使之从零开始增加。

同时，观察仿真曲线的变化,并给出过阻尼、临界、欠阻尼的条件。

当K=0时的仿真曲线当K=1时的仿真曲线当K=2.5时的仿真曲线当K=3。

5时的仿真曲线当K=4时的仿真曲线根据调整比例系数K，使之从零开始增加，同时观察仿真曲线的变化，得出以下结论；过阻尼的条件：K>2.5时；临界阻尼条件：K=2.5时；欠阻尼的条件：K<2。

MATLAB软件简介1.1 MATLAB软件在控制系统中的应用介绍MATLAB的名称源自Matrix Laboratory，1984年由美国Mathworks公司推向市场。

它是一种科学计算软件，专门以矩阵的形式处理数据。

MA TLAB将高性能的数值计算和可视化集成在一起，并提供了大量的内置函数，从而被广泛地应用于科学计算、控制系统、信息处理等领域的分析、仿真和设计工作。

1993年MathWorks公司从加拿大滑铁卢大学购得MAPLE软件的使用权，从而以MAPLE为“引擎”开发了符号数学工具箱（Symbolic Math Toolbox）。

MATLAB软件包括五大通用功能：数值计算功能（Nemeric）；符号运算功能（Symbolic）；数据可视化功能（Graphic）；数据图形文字统一处理功能（Notebook）和建模仿真可视化功能（Simulink）。

其中，符号运算功能的实现是通过请求MAPLE内核计算并将结果返回到MA TLAB命令窗口。

该软件有三大特点：一是功能强大；二是界面友善、语言自然；三是开放性强。

目前，Mathworks公司已推出30多个应用工具箱。

MA TLAB在线性代数、矩阵分析、数值及优化、数理统计和随机信号分析、电路与系统、系统动力学、信号和图像处理、控制理论分析和系统设计、过程控制、建模和仿真、通信系统、以及财政金融等众多领域的理论研究和工程设计中得到了广泛应用。

MATLAB在控制系统中的应用主要包括符号运算和数值计算仿真分析。

由于控制系统课程的许多内容都是基于公式演算，而MATLAB借助符号数学工具箱提供的符号运算功能能基本满足控制系统课程的需求。

例如，解微分方程、傅里叶正反变换、拉普拉斯正反变换、z正反变换等。

MA TLAB在控制系统中的另一主要应用是数值计算与仿真分析，主要包括函数波形绘制、函数运算、冲激响应与阶跃响应仿真分析、信号的时域分析、信号的频谱分析、系统的S域分析、零极点图绘制等内容。

现代控制理论MATLAB 实现例6.1.2系统的线性化模型如下[]xCx y ux Bu Ax x 0001101001100100001000010.==⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=+=其中x 是系统的状态变量，y 是小车的位移，u 是作用小车的力 1在Ae e =.作用下的误差如下。

M 文件如下得到的如下的结果：设计一个状态观测器，使得观测器极点是10,10,322,3224321-=-=+-=+-=u u j u j u解 观测器模型如下Ly Bu x LC A x++-=~.)(~运行如下m 文件状态估计的误差状态方程为：e LC A e )(.-=以下进一步通过仿真来检验观测器的效果，取初始误差向量为[]Te 1.01.021)0(-=执行如下m 文件状态估计的误差曲线如下降维观测器的题：例6,3,2考虑系统Cxy Bu Ax x =+=.其中，[]001,100,6116100010=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=C B A 设计一个具有极点u1=-10,u2=-10,的降维的观测器。

因此降阶观测器的增益矩阵是L=[]T514,具有期望极点的降阶观测器为u y w w ⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--+⎥⎦⎤⎢⎣⎡---=10260191616114~.~跟踪控制器的设计例5.4.1已知被控对象的状态空间模型为[]xy u x x 21104310.=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--= 设计状态反馈控制器，使得闭环极点为-4和-5，和跟踪控制器。

并讨论闭环系统的稳态性能。

可以知道能稳定跟踪先判断是否能稳定跟踪可以得到如下的结果00.511.522.530.20.40.60.811.21.4time(sec)O u t p u t最优控制的习题例7.2.2考虑以下状态空间模型的描述的系统：其中⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=100,92735100010B A系统的性能指标J 定义为 ⎰∞+=)(t T T d Ru u Qx x J其中，[]1,100010001=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=R Q 设计最优状态反馈控制器，并检验最优闭环系统对初始状态[]Tx 001)0(=的响应。

现代控制系统分析与设计——基于matlab的仿真与实现近年来，随着工业技术的飞速发展，控制系统逐渐成为工业自动化过程中不可缺少的重要组成部分，因此其分析与设计也会受到人们越来越多的关注。

本文从控制系统的分类出发，介绍了基于Matlab 的分析与仿真方法，并结合详细的实例，展示了最新的Matlab软件如何用来设计现代控制系统，及如何实现仿真结果。

一、控制系统分类控制系统是将完整的物理系统划分为几个部分，通过规定条件把这些部分组合起来，共同完成某一特定任务的一种技术。

控制系统可分为离散控制系统和连续控制系统，离散控制系统的尺度以脉冲的形式表现，而连续控制系统的尺度以连续变量的形式表现，常见的连续控制系统有PID、环路反馈控制等。

二、基于Matlab的分析与仿真Matlab是一款实用的高级计算和数学工具，具有智能语言功能和图形用户界面，可以进行复杂数据分析和可视化。

Matlab可以用来开发控制系统分析与仿真，包括：数学建模，系统建模，状态估计与观测，数据处理，控制算法研究，仿真实验及系统原型开发等。

此外，Matlab还可以利用其它技术，比如LabVIEW或者C程序，将仿真结果实现在实物系统上。

三、实现现代控制系统分析与设计基于Matlab的现代控制系统分析与设计，需要从以下几个方面进行考虑。

1.数学建模：Matlab支持多种数学计算，比如代数运算、矩阵运算、曲线拟合等，可以用来建立控制系统的数学模型。

2.系统建模：Matlab可以用于控制系统的建模和仿真，包括并行系统建模、混沌建模、非线性系统建模、时滞建模、系统设计建模等。

3.状态估计与观测：Matlab可以用来计算系统状态变量，并且可以根据测量信号估计系统状态，用于系统诊断和控制。

4.数据处理：Matlab可以用来处理控制系统中的大量数据，可以更好地研究控制系统的特性，以便进行更好的设计和控制。

5.算法研究：Matlab可以用来研究新的控制算法，以改进控制系统的性能。

现代控制理论的MATLAB编程。

现代控制理论实验报告名称:班级:学生编号:目标1。

实验设备2。

实验目标3。

实验步骤实验设备:1台PC机和1个MATLAB软件。

第二，实验的目的1。

学习建立系统状态空间表达式的方法和理解系统状态空间表达式与传递函数之间转换的方法；2.通过编程，在计算机上调试，掌握系统状态空间表达式和传递函数之间相互转换的方法；3.学习如何使用MATLAB。

三.实验步骤1.根据给定的系统结构图，写出死循环系统的传递函数。

如果K=10且T=0.1，步进输出下的系统输出响应应使用MATLAB编程。

2.在MATLAB界面下调试程序，并检查其运行是否正确。

3.给出固定二阶系统的结构图:图为二阶系统结构图(1)求闭环循环传递函数(S)===(2)如果K=10，T=0.1，仿真给出了系统在阶次跳变下的输出响应。

将KT代入方程，得到φ (S)==1)系统响应曲线由MATLAB命令得到，在MATLAB上输入以下命令:num=[100]；den=[1，10，100]；在步骤(num，den)程序运行之后显示的时域动态响应曲线(如图2所示)是时域动态响应曲线2)。

模拟Simulink启动Simulink，打开空白模块编辑窗口，绘制所需模块并给出正确参数。

所有绘制的模块被链接(如图1所示)以形成原始系统的框图描述(如图3所示)。

选择模拟控制参数开始模拟过程。

模拟结果示波器如图4所示。

图3二阶系统的Simulink(仿真)图4仿真结果示波器显示(仿真输出)(3)调整比例因子k从零开始增加。

同时，观察仿真曲线的变化，给出过阻尼、临界阻尼和欠阻尼的条件。

K=0时的仿真曲线、K=1时的仿真曲线、K=2.5时的仿真曲线、K=3.5时的仿真曲线以及K=4时的仿真曲线根据缩放因子K的调整从零开始增加。

同时，观察仿真曲线的变化，并得出以下结论。

过阻尼的条件:2.5小时；临界阻尼条件:当K=2.5时；阻尼不足的条件:克努姆=[100]；den=[1，10，100]；G=tf(数字，den)。

现代控制理论习题解答与Matlab程序⽰例现代控制理论习题解答与Matlab程序⽰例现代控制理论第三版课后习题参考解答：下⾯给出部分书后习题的Matlab⽅法求解：第⼀章状态空间表达式1 传递函数转为状态空间表达式和约旦标准型num=[10,-10];den=[1,4,3,0];w=tf(num,den);se=ss(w)[T,J]=jordan(A)对应习题1-62 状态空间表达式转为传递函数A=[0,1,0;-2,-3,0;-1,1,-3];B=[0;1;2];C=[0,0,1];D=0;se=ss(A,B,C,D);w=tf(se)对应习题1-7第⼆章状态空间表达式的解A=[0,1;0,0];B=[0;1];C=[1,0];D=0;se=ss(A,B,C,D);[y,t,x]=step(se);figure(1);plot(t,x);figure(2);plot(t,y);对应习题2-6第三章能控性和能观性1 能控性和能观性判定A=[-3,1;1,-3];B=[1,1;1,1];C=[1,1;1,-1];M=[B,A*B];N=[C;C*A];n=length(A);rank(M)if rank(M)==ndisp('系统可控')elsedisp('系统不可控')endrank(N)if rank(N)==ndisp('系统可观')elsedisp('系统不可观')end[T,J]=jordan(A);T'*BC*T2 能控标准型A=[1 -2;3 4];B=[1;1];C=[0 0];D=0;G=ss(A,B,C,D);M=[B,A*B];n=length(A);rank(M)if rank(M)==ndisp('系统可控')elsedisp('系统不可控')endQc=ctrb(A,B);Cm=[0 1]*inv(Qc);Cm2=inv([Cm;Cm*A]);sysc=ss2ss(G,inv(Cm2))对应习题3-73 能观标准型A=[1,-1;1,1];B=[2;1];C=[-1 1];D=0;G=ss(A,B,C,D);M=[B,A*B];N=[C;C*A];n=length(A);rank(M)if rank(M)==ndisp('系统可控')elsedisp('系统不可控')endrank(N)if rank(N)==ndisp('系统可观')elsedisp('系统不可观')endQc=ctrb(A,B);Cm=[0 1]*inv(Qc);Cm2=inv([Cm;Cm*A]);sysc=ss2ss(G,inv(Cm2))Qo=obsv(A,C);Om=inv(Qo)*[0;1];Om2=[Om A*Om];syso=ss2ss(G,inv(Om2))对应习题3-84 传递函数转能控或能观标准型num=[1,6,8];den=[1,4,3];[A,B,C,D]=tf2ss(num,den);G=ss(A,B,C,D);M=[B,A*B];N=[C;C*A];n=length(A);rank(M)if rank(M)==ndisp('系统可控')elsedisp('系统不可控')endrank(N)if rank(N)==ndisp('系统可观')elsedisp('系统不可观')endCm=[0 1]*inv(Qc);Cm2=inv([Cm;Cm*A]);sysc=ss2ss(G,inv(Cm2))Qo=obsv(A,C);Om=inv(Qo)*[0;1];Om2=[Om A*Om];syso=ss2ss(G,inv(Om2))对应习题3-9第四章李雅普诺夫⽅法和稳定性1 李雅普诺夫定理第⼀⽅法A=[-3 -6 -2 -1;1 0 0 0;0 1 0 0;0 0 1 0]; B=[1;0;0;0];C=[0 0 1 1];D=[0];flag=0;[z,p,k]=ss2zp(A,B,C,D,1);disp('系统零点，极点和增益为：');zpkn=length(A);for i=1:nif real(p(i))>0flag=1;endendif flag==1disp('系统不稳定');elsedisp('系统稳定');end通过极点判定系统是否稳定2 李雅普诺夫定理第⼆⽅法A=[-3 -6 -2 -1;1 0 0 0;0 1 0 0;0 0 1 0]; Q=eye(4,4);P=lyap(A,Q);flag=0;n=length(A);for i=1:ndet(P(1:i,1:i))if(det(P(1:i,1:i))<=0)flag=1;endendif flag==1disp('系统不稳定');elsedisp('系统稳定');end通过P是否正定判定系统是否稳定。

现代控制理论及其MATLAB实践课程设计一、前言现代控制理论是电子信息类学科中的重要基础课程，本门课程主要介绍现代控制理论的内容以及如何运用MATLAB进行实际计算和仿真实践。

这门课程的目的在于掌握现代控制理论基础知识，熟悉控制系统的数学模型，能够使用MATLAB实现控制策略和算法，以及评价系统的性能，为学生今后的工程实践打下坚实基础。

二、课程大纲1. 控制系统基础知识•控制系统的基本概念和分类•系统建模的方法与技巧•信号与系统的基本原理•控制系统的基本结构2. 线性系统理论•系统传递函数及其性质•系统稳定性分析•系统稳定性判据•实际系统的频率响应分析3. 分布式控制系统•分布式控制系统的基本概念•分布式控制系统的信号传递与通信•分布式控制系统的分析与设计•广域网络上的分布式协同控制4. MATLAB模拟与实践•MATLAB基本操作和编程技巧•线性系统建模及仿真•控制策略和算法设计•控制系统的性能评价和优化三、课程设计本门课程的设计旨在提高学生的实际操作能力和创新思维能力，具体安排如下：1. 实验教学环节本课程将采用小班教学，分为理论课和实验课两个环节。

实验教学环节有以下几方面内容：•实验一：MATLAB基础操作练习•实验二：建立线性系统的模型及其控制•实验三：分布式控制系统设计和实现•实验四：MATLAB仿真结果分析及评价2. 课程设计要求每个小组的组长需要编写一个小组实验报告，其中要求包括以下内容：•实验目的、原理和方案•实验步骤详解和MATLAB代码实现•实验数据处理和仿真结果分析•实验心得与体会在每个实验课后，小组同学之间需要进行合作协作，并在组长指导下共同完成实验报告的撰写和提交。

四、总结通过本门课程的学习和实践，学生能够深入理解现代控制理论的基本原理及其应用，在MATLAB仿真环境下逐步掌握系统建模、控制策略设计和控制系统性能评价等关键步骤。

同时，本课程的课程设计能够培养学生的实际操作能力和创新思维能力，为他们今后的工程实践打下坚实基础。

Matlab在《现代控制理论》教学中的运用摘要：Matlab软件是进行控制系统分析与计算的辅助工具，通过应用Matlab软件对控制系统的分析与计算的实例，说明Matlab可以计算控制系统的参数，使控制问题变得简单，从而可以提高学生的学习效率，提高学习兴趣。

《现代控制理论》教学中，Matlab是分析系统的有效工具。

关键词：Matlab；现代控制理论；系统《现代控制理论》为自动化及相关专业的本科生开设的课程。

现代控制理论是建立在状态空间法基础上的，其对控制系统的分析与设计主要是通过对系统的状态方程来描述，主要方法就是时间域方法。

包括线性系统和非线性系统，定常系统和时变系统，单输入单输出系统和多输入多输出系统。

现代控制理论的控制系统的分析与设计中采用了现代数学作为工具，因此，将带来大量的计算。

在《现代控制理论》的教学中，如果系统的设计等都采用手算的方法，显然是不太合适的。

Matlab是matrix和laboratory两个词的组合，意为矩阵实验室，用于数值计算、系统分析、系统的仿真，Matlab 不断发展的工具箱使其日益丰富，作为一个功能强大的软件平台，它代表了当今国际科学计算软件的先进水平。

在《现代控制理论》教学中，利用Matlab来计算控制系统的计算与仿真问题，可以加深对《现代控制理论》这门课的理解，形成良好的互动。

本文将对《现代控制理论》教学中Matlab的应用做些探讨。

一、Matlab在系统稳定性分析中李雅普诺夫处理方法中的应用例，应用李雅普诺夫方程方法分析系统稳定性。

解：原点是系统的唯一平衡点。

解李雅普诺夫方程 ATP+PA=-1系统是二阶的，故P=P11 P12P12 P22x将矩阵A和P的表达式带入李雅普诺夫方程中，得得方程组-2P12=-12P11-P12-P22=04P12-2P22=-1求解方程组，可得P11 P12P12 P22=1验证矩阵P的正定性，算得P的各阶行列式都大于0，故P为正定的，故系统是渐近稳定的。

实验一 状态空间的Matlab 描述实验目的：1、 熟悉Matlab 中矩阵的基本输入与运算（包括加、减、乘、求逆、转置等运算）；2、 熟练掌握利用Matlab 建立控制系统的数学模型及进行线性变换的方法；3、 掌握利用simulink 搭建控制系统的方法。

实验内容：1、 矩阵的基本输入与运算：给定两个矩阵，求其加、减、乘、逆阵(求取矩阵逆阵的函数为inv （）)及转置，进行乘、逆阵运算时，注意行列限制。

2、 利用Matlab 建立系统的各种数学模型：A 、 传递函数模型1110111)()()(a s a s a s b s b s b s b s U s Y s W n n n m m m m ++++++++==---- 用以下命令建立传递函数模型：),(den num tf sys =],,,[01b b b num m m -= 表示传函分子向量，各元素为分子多项式中各项系数，阶次由高到低； ],,,,1[021a a a den n n --= 表示传函分母向量，各元素为分母多项式中各项系数，阶次由高到低。

注意：若多项式中有缺项，则向量中相应位置处系数为0；若为多输入-多输出系统，则i b 为r m ⨯实系数矩阵，num 的行数与输出变量的个数相等。

B 、 零极点增益模型∏∏==--=n j j m i i g ps z s K s W 11)()()( ),,(k p z zpk sys = ],,,[21m z z z z = 表示零点],,,[21n p p p p = 表示极点][g k k = 表示增益C 、 状态空间模型⎩⎨⎧+=+=DuCx y Bu Ax x ),,,(D C B A ss sys = 利用系统矩阵、输入矩阵、输出矩阵、直接传递矩阵即可建立系统的状态空间模型。

若直接传递矩阵为零矩阵，可使用),(r m zeros 来建立一个r m ⨯的零矩阵。

3、 在各种模型之间进行转换：A 、传递函数模型转换为零极点增益模型 ),(2],,[den num zp tf k p z =B 、零极点增益模型转换为传递函数模型 ),,(2],[k p z tf zp den num =C 、传递函数模型转换为状态空间模型 ),(2],,,[den num ss tf d c b a =D 、状态空间模型转换为传递函数模型 ),,,,(2],[i d c b a tf ss den num =最后一个参数要指出是第i 个输入到全部输出之间的传递函数模型E 、零极点增益模型转换为状态空间模型 ),,(2],,,[k p z ss zp d c b a =F 、状态空间模型转换为零极点模型 ),,,,(2],,[i d c b a zp ss k p z =最后一个参数要指出是第i 个输入到全部输出之间的传递函数模型。

实验一利用MATLAB进行线性系统的模型转换及联结课程：现代控制理论姓名：学号：班级：指导教师：标题 (1)目录 (2)一实验目的： (3)二实验原理： (3)三实验步骤： (6)四实验要求： (7)五实验内容： (8)1 (8)2 (18)3 (29)4 (36)5 (37)六实验感想： (40)一 实验目的：1、学习系统状态空间模型的建立方法、了解状态空间模型与传递函数、零极点模型之间相互转换的方法；2、通过编程、上机调试，掌握系统状态空间模型与传递函数相互转换的方法。

3、通过编程、上机调试，掌握系统模型的联结方法。

二 实验原理： 一、连续系统（1）状态空间模型x Ax Buy Cx Du=+=+ （1.1）其中：nx R ∈是系统的状态向量，mu R ∈是控制输入，py R ∈是测量输出，A 是n n ⨯维状态矩阵、B 是n m ⨯维输入矩阵、C 是p n ⨯维输出矩阵、D 是直接转移矩阵。

在MATLAB 中，用（A,B,C,D ）矩阵组表示。

系统传递函数和状态空间模型之间的关系如式（1.2）所示。

1()()G s C sI A B D -=-+ （1.2）（2）传递函数模型11101110()(),()m m m m n n n n b s b s b s b num s H s m n den s a s a s a s a ----++++==≤++++ 在MA TLAB 中，直接用分子/分母的系数表示1010[,,,][,,,]m m n n num b b b den a a a --==（3）零极点增益模型1212()()()()()()()m n s z s z s z H s ks p s p s p ---=---在MA TLAB 中，用[z, p, k]矢量组表示，即1212[,,,];[,,,];[];m n z z z z p p p p k k ===二、离散系统（1）传递函数模型11101110()m m m m n n n n b z b z b z b H z a z a z a z a ----++++=++++ （2）零极点增益模型1212()()()()()()()m n z z z z z z H z kz p z p z p ---=---（3）状态空间模型(1)()()()()()x k Ax k Bu k y k Cx k Du k +=+=+三、三种模型间的转换表示状态空间模型和传递函数的MA TLAB 函数。