现代控制理论的MATLAB实现共31页

现代控制原理matlab实验报告实验一.利用MATLAB进行线性系统的模型转换及联结一．实验目的1、学习系统状态空间模型的建立方法、了解状态空间模型与传递函数、零极点模型之间相互转换的方法；2、通过编程、上机调试，掌握系统状态空间模型与传递函数相互转换的方法。

3、通过编程、上机调试，掌握系统模型的联结方法。

二．实验步骤1、根据所给系统的已知条件，如传递函数、零极点模型或（A 、B 、C 、D ），实现状态空间模型、传递函数模型、零极点增益模型之间的转换，采用MATLAB 的相关函数编写m -文件。

2、应用系统建模工具，并联、串联、闭环、反馈等函数解决实际问题。

3、在MA TLAB 界面下调试程序。

三．实验要求1．在运行以上例程序的基础上，应用MA TLAB 求下面传递函数阵的状态空间实现232252()234s s s G s s s s +⎡⎤⎢⎥++⎣⎦=+++提示：num =[0 0 1 2；0 1 5 3] 解：num=[0 0 1 2;0 1 5 2]; den=[1 2 3 4];[A,B,C,D]=tf2ss(num,den) A =-2 -3 -4 1 0 0 0 1 0 B =1 0 0 C =0 1 2 1 5 2 D =0 02．一个双输入双输出系统112233412311022711353x x x x u x x -⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦⎣⎦11223120011x y x y x ⎡⎤⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎣⎦求出此模型的能控标准型和能观标准型。

提示：写出两个子系统的传递函数模型，进而求出这两个传递函数模型的能控标准型实现或能观标准型实现，讨论是否能通过子系统的能控标准型实现或能观标准型实现求出原来系统的能控标准型和能观标准型。

解：A=[4 1 -2;1 0 2;1 -1 3]; B=[3 1;2 7;5 3]; C=[1 2 0;0 1 1]; D=[0];[num1,den1]=ss2tf(A,B1,C1,D) [num2,den2]=ss2tf(A,B2,C2,D)得到： num1 =0 7.0000 -19.0000 -36.0000den1 =1.0000 -7.0000 15.0000 -9.0000num2 =0 10.0000 -60.0000 98.0000den2 =1.0000 -7.0000 15.0000 -9.0000实验二.利用MATLAB 求取线性系统的状态空间模型的解并分析其稳定性一. 实验目的1、根据状态空间模型分析系统由初始状态和外部激励所引起的响应；2、了解系统稳定性的判定方法（直接法和间接法）；3、通过编程、上机调试，掌握系统运动的分析方法。

MATLAB与控制理论实验教程编著汪宁郭西进机械工业出版社第五章自动控制系统的数字计算机仿真自动控制系统仿真是系统仿真的一个重要分支，它是一门涉及自动控制理论、计算数学、计算机技术、系统辨识、控制工程以及系统科学的综合性新型学科。

它为控制系统的分析、计算、研究、综合设计以及自动控制系统的计算机辅助教学等提供了快速、经济、科学等有效的手段。

控制系统的验证中，所有的组成部分都是数学模型，这种控制系统的验证实验称为数字仿真，数字仿真可以在计算机设备上完成，所以也称计算机仿真。

实际上计算机仿真是指以计算机为主要工具，对系统进行实验研究的一种方法。

目的就是对控制系统的稳定性、动态品质、控制精度等性能进行计算验证。

计算机仿真可分为以下四步：（1）建立系统的数学模型系统的数学模型，是描述系统输入、输出变量以及内部各变量之间关系的数学表达式。

描述自动控制系统诸变量间静态关系的数学表达式，称为静态模型；描述自动控制系统动态关系的数学表达式，称为动态模型。

最常用的基本数学模型就是微分方程与差分方程。

对于一般系统来说，可以通过某些定律来建立数学模型；但是对于复杂系统，则必须通过系统辨识技术，考虑计算所要求的精度，略去一些次要因素，使模型既能够准确地反映系统的动态本质，又能够简化分析计算的工作，通过实验法建立数学模型。

数学模型是系统仿真的依据，所以数学模型的准确性是十分重要的。

（2）建立系统的仿真模型原始的自动控制系统的数学模型比如微分方程，并不能用来直接对系统进行仿真，还需将其转换为能够对系统进行仿真的模型。

对于连续系统而言，将像微分方程这样的原始数学模型，在零初始条件下进行拉普拉斯变换，求得自动控制系统的传递函数之类的数学模型。

以传递函数模型为基础，等效变换为状态空间模型，或者将其图形化为动态结构图模型，这些模型都是自动控制系统的仿真模型。

（3）选择算法，编制系统的仿真程序对于非实时系统的仿真，可以用一般的高级语言编制仿真程序。

北京交通⼤学现代控制理论matlab实验报告实验⼀利⽤MATLAB进⾏线性系统的模型转换及联结课程：现代控制理论姓名：王柬⽂学号：11212070班级：⾃动化1103指导教师：张勇标题 (1)⽬录 (2)⼀实验⽬的： (3)⼆实验原理： (3)三实验步骤： (6)四实验要求： (7)五实验内容： (8)1 (8)2 (18)3 (29)4 (36)5 (37)六实验感想： (40)⼀实验⽬的：1、学习系统状态空间模型的建⽴⽅法、了解状态空间模型与传递函数、零极点模型之间相互转换的⽅法；2、通过编程、上机调试，掌握系统状态空间模型与传递函数相互转换的⽅法。

3、通过编程、上机调试，掌握系统模型的联结⽅法。

⼆实验原理：⼀、连续系统（1）状态空间模型x Ax Buy Cx Du=+=+& （1.1）其中：nx R ∈是系统的状态向量，mu R ∈是控制输⼊，py R ∈是测量输出，A 是n n ?维状态矩阵、B 是n m ?维输⼊矩阵、C 是p n ?维输出矩阵、D 是直接转移矩阵。

在MATLAB 中，⽤（A,B,C,D ）矩阵组表⽰。

系统传递函数和状态空间模型之间的关系如式（1.2）所⽰。

1()()G s C sI A B D -=-+ （1.2）（2）传递函数模型11101110()(),()m m m m n n n n b s b s b s b num s H s m n den s a s a s a s a ----++++==≤++++L L 在MATLAB 中，直接⽤分⼦/分母的系数表⽰1010[,,,][,,,]m m n n num b b b den a a a --==L L（3）零极点增益模型1212()()()()()()()m n s z s z s z H s ks p s p s p ---=---L L在MATLAB 中，⽤[z, p, k]⽮量组表⽰，即1212[,,,];[,,,];[];m n z z z z p p p p k k ===L L ⼆、离散系统（1）传递函数模型11101110()m m m m n n n n b z b z b z b H z a z a z a z a ----++++=++++L L （2）零极点增益模型1212()()()()()()()m n z z z z z z H z kz p z p z p ---=---L L（3）状态空间模型(1)()()()()()x k Ax k Bu k y k Cx k Du k +=+=+三、三种模型间的转换表⽰状态空间模型和传递函数的MATLAB 函数。

MATLAB软件简介1.1 MATLAB软件在控制系统中的应用介绍MATLAB的名称源自Matrix Laboratory，1984年由美国Mathworks公司推向市场。

它是一种科学计算软件，专门以矩阵的形式处理数据。

MA TLAB将高性能的数值计算和可视化集成在一起，并提供了大量的内置函数，从而被广泛地应用于科学计算、控制系统、信息处理等领域的分析、仿真和设计工作。

1993年MathWorks公司从加拿大滑铁卢大学购得MAPLE软件的使用权，从而以MAPLE为“引擎”开发了符号数学工具箱（Symbolic Math Toolbox）。

MATLAB软件包括五大通用功能：数值计算功能（Nemeric）；符号运算功能（Symbolic）；数据可视化功能（Graphic）；数据图形文字统一处理功能（Notebook）和建模仿真可视化功能（Simulink）。

其中，符号运算功能的实现是通过请求MAPLE内核计算并将结果返回到MA TLAB命令窗口。

该软件有三大特点：一是功能强大；二是界面友善、语言自然；三是开放性强。

目前，Mathworks公司已推出30多个应用工具箱。

MA TLAB在线性代数、矩阵分析、数值及优化、数理统计和随机信号分析、电路与系统、系统动力学、信号和图像处理、控制理论分析和系统设计、过程控制、建模和仿真、通信系统、以及财政金融等众多领域的理论研究和工程设计中得到了广泛应用。

MATLAB在控制系统中的应用主要包括符号运算和数值计算仿真分析。

由于控制系统课程的许多内容都是基于公式演算，而MATLAB借助符号数学工具箱提供的符号运算功能能基本满足控制系统课程的需求。

例如，解微分方程、傅里叶正反变换、拉普拉斯正反变换、z正反变换等。

MA TLAB在控制系统中的另一主要应用是数值计算与仿真分析，主要包括函数波形绘制、函数运算、冲激响应与阶跃响应仿真分析、信号的时域分析、信号的频谱分析、系统的S域分析、零极点图绘制等内容。

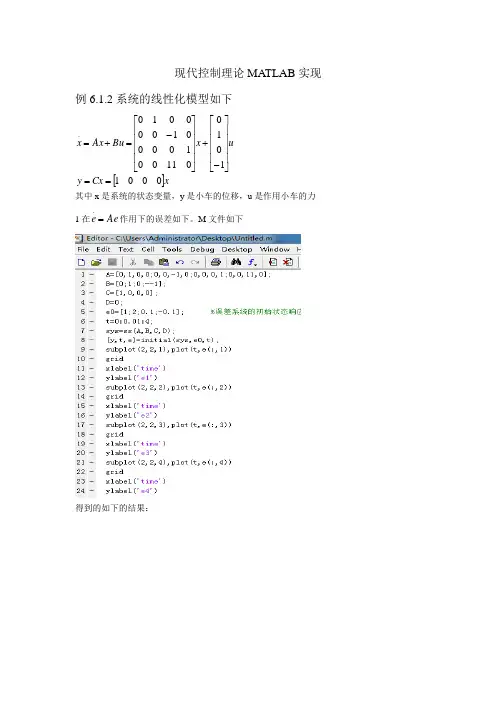
现代控制理论MATLAB 实现例6.1.2系统的线性化模型如下[]xCx y ux Bu Ax x 0001101001100100001000010.==⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=+=其中x 是系统的状态变量，y 是小车的位移，u 是作用小车的力 1在Ae e =.作用下的误差如下。

M 文件如下得到的如下的结果：设计一个状态观测器，使得观测器极点是10,10,322,3224321-=-=+-=+-=u u j u j u解 观测器模型如下Ly Bu x LC A x++-=~.)(~运行如下m 文件状态估计的误差状态方程为：e LC A e )(.-=以下进一步通过仿真来检验观测器的效果，取初始误差向量为[]Te 1.01.021)0(-=执行如下m 文件状态估计的误差曲线如下降维观测器的题：例6,3,2考虑系统Cxy Bu Ax x =+=.其中，[]001,100,6116100010=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=C B A 设计一个具有极点u1=-10,u2=-10,的降维的观测器。

因此降阶观测器的增益矩阵是L=[]T514,具有期望极点的降阶观测器为u y w w ⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--+⎥⎦⎤⎢⎣⎡---=10260191616114~.~跟踪控制器的设计例5.4.1已知被控对象的状态空间模型为[]xy u x x 21104310.=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--= 设计状态反馈控制器，使得闭环极点为-4和-5，和跟踪控制器。

并讨论闭环系统的稳态性能。

可以知道能稳定跟踪先判断是否能稳定跟踪可以得到如下的结果00.511.522.530.20.40.60.811.21.4time(sec)O u t p u t最优控制的习题例7.2.2考虑以下状态空间模型的描述的系统：其中⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=100,92735100010B A系统的性能指标J 定义为 ⎰∞+=)(t T T d Ru u Qx x J其中，[]1,100010001=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=R Q 设计最优状态反馈控制器，并检验最优闭环系统对初始状态[]Tx 001)0(=的响应。

昆明理工大学机电学院机械工程专业研究生实验《现代控制工程》MATLA实验指导书昆明理工大学机电工程学院现代控制工程》MATLAB 实验指导书一、MATLAB 简介1 MATLAB 概述MATLAB 是MA Trix LABoratory 的缩写，早期主要用于现代控制中复杂的矩阵、向量的各种运算。

由于MA TLAB 提供了强大的矩阵处理和绘图功能，很多专家因此在自己擅长的领域用它编写了许多专门的MATLAB 工具包( toolbox )，如控制系统工具包( control systems toolbox )；系统辨识工具包( system identification toolbox )；信号处理工具包( signal processing toolbox )；鲁棒控制工具包( robust control toolbox )；最优化工具包(optimization toolbox )等等。

由于MA TLAB 功能的不断扩展，所以现在的MATLAB 已不仅仅局限与现代控制系统分析和综合应用，它已是一种包罗众多学科的功能强大的“技术计算语言( TheLanguage of Technical Computing )”。

MathWorks 公司于1992 年推出了具有划时代意义的MATLAB 4.0 版本，并推出了交互式模型输入与仿真系统SIMULINK ，它使得控制系统的仿真与CAD 应用更加方便、快捷，用户可以方便地在计算机上建模和仿真实验。

1997 年MathWorks 推出的MA TLAB 5.0 版允许了更多的数据结构，1999 年初推出的MA TLAB 5.3 版在很多方面又进一步改进了MATLAB 语言的功能。

2000 年底推出的MATLAB 6.0 。

最新版本是MA TLAB7.0 。

MATLAB 以矩阵作为基本编程单元，它提供了各种矩阵的运算与操作，并有较强的绘图功能。

MATLAB 集科学计算、图像处理、声音处理于一身，是一个高度的集成系统，有良好的用户界面，并有良好的帮助功能。

现代控制理论的MATLAB编程。

现代控制理论实验报告名称:班级:学生编号:目标1。

实验设备2。

实验目标3。

实验步骤实验设备:1台PC机和1个MATLAB软件。

第二，实验的目的1。

学习建立系统状态空间表达式的方法和理解系统状态空间表达式与传递函数之间转换的方法；2.通过编程，在计算机上调试，掌握系统状态空间表达式和传递函数之间相互转换的方法；3.学习如何使用MATLAB。

三.实验步骤1.根据给定的系统结构图，写出死循环系统的传递函数。

如果K=10且T=0.1，步进输出下的系统输出响应应使用MATLAB编程。

2.在MATLAB界面下调试程序，并检查其运行是否正确。

3.给出固定二阶系统的结构图:图为二阶系统结构图(1)求闭环循环传递函数(S)===(2)如果K=10，T=0.1，仿真给出了系统在阶次跳变下的输出响应。

将KT代入方程，得到φ (S)==1)系统响应曲线由MATLAB命令得到，在MATLAB上输入以下命令:num=[100]；den=[1，10，100]；在步骤(num，den)程序运行之后显示的时域动态响应曲线(如图2所示)是时域动态响应曲线2)。

模拟Simulink启动Simulink，打开空白模块编辑窗口，绘制所需模块并给出正确参数。

所有绘制的模块被链接(如图1所示)以形成原始系统的框图描述(如图3所示)。

选择模拟控制参数开始模拟过程。

模拟结果示波器如图4所示。

图3二阶系统的Simulink(仿真)图4仿真结果示波器显示(仿真输出)(3)调整比例因子k从零开始增加。

同时，观察仿真曲线的变化，给出过阻尼、临界阻尼和欠阻尼的条件。

K=0时的仿真曲线、K=1时的仿真曲线、K=2.5时的仿真曲线、K=3.5时的仿真曲线以及K=4时的仿真曲线根据缩放因子K的调整从零开始增加。

同时，观察仿真曲线的变化，并得出以下结论。

过阻尼的条件:2.5小时；临界阻尼条件:当K=2.5时；阻尼不足的条件:克努姆=[100]；den=[1，10，100]；G=tf(数字，den)。