电路分析答案解析第五章

电路分析智慧树知到课后章节答案2023年下上海电力大学上海电力大学第一章测试1.图示电路中,节点A和B之间的电压ＵAB为（）V。

A:19 B:16 C:-16 D:21答案:-162.图示电路中Ｉ= 0 时,电位ＵA=（）V。

A:70 B:90 C:-10 D:60答案:603.通常所说负载增加，是指负载（）增加。

A:电阻 B:功率 C:电流 D:电压答案:功率4.图示电路中Ｓ断开时Ｉ1= 0A,Ｉ=2A。

Ｓ闭合时Ｉ1=( )A,Ｉ=( )A。

（）A:3 B:0 C:6 D:2答案:0;65.图示电路中,当ＩS=10A 时,电压Ｕ为（）V,当ＩS=8A时电压Ｕ为（）V。

（）A:0 B:16 C:12 D:8答案:16;126.电路理论分析的对象是电路模型而不是实际电路。

（）A:错 B:对答案:对7.欧姆定律可表示成U=RI,也可表示成U=-RI,这与采用的参考方向有关。

（）A:对 B:错答案:对8.在节点处各支路电流的方向不能均设为流向节点，否则将只有流入节点的电流而无流出节点的电流。

（）A:错 B:对答案:错9.在电压近似不变的供电系统中，负载增加相当于负载电阻减少。

（）A:错 B:对答案:对10.理想电压源的端电压是由它本身确定的，与外电路无关，因此流过它的电流则是一定的，也与外电路无关。

（）A:对 B:错答案:错第二章测试1.图示电路ＡＢ间的等效电阻为（）。

A:24Ω B:14Ω C:12Ω D:10.67Ω答案:14Ω2.电路如图所示，Ａ、Ｂ端的等效电阻Ｒ＝（）。

A:5Ω B:4Ω C:10Ω D:20Ω答案:4Ω3.电路如图所示，可化简为（）A:不能化简B:8Ω电阻C:13Ω电阻D:3Ω电阻答案:3Ω电阻4.如图所示电路中，当电阻Ｒ2增加时电流Ｉ将（）。

A:不变 B:增加 C:减小答案:增加5.图示电路中，就其外特性而言，（）。

A:ａ、ｄ等效 B:ａ、ｂ、ｃ、ｄ均等效 C:ａ、ｂ等效 D:ｂ、ｃ等效答案:ｂ、ｃ等效6.两只额定电压为110V的电灯泡串联起来总可以接到220V的电压源上使用。

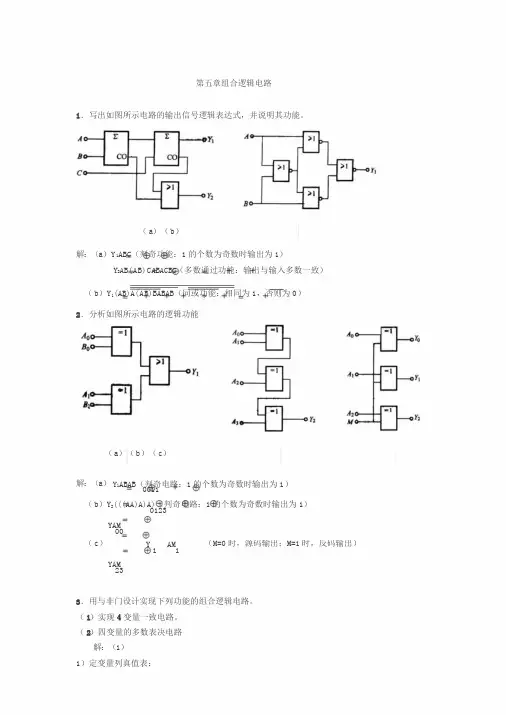
第五章组合逻辑电路1．写出如图所示电路的输出信号逻辑表达式，并说明其功能。

（a）（b）解：（a）Y1ABC（判奇功能：1的个数为奇数时输出为1）Y2AB(AB)CABACBC（多数通过功能：输出与输入多数一致）（b）Y1(AB)A(AB)BABAB（同或功能：相同为1，否则为0）2．分析如图所示电路的逻辑功能（a）（b）（c）解：（a）Y1ABAB（判奇电路：1的个数为奇数时输出为1）0011（b）Y2(((AA)A)A)（判奇电路：1的个数为奇数时输出为1）0123YAM00（c）Y1 A M1（M=0时，源码输出；M=1时，反码输出）YAM233．用与非门设计实现下列功能的组合逻辑电路。

（1）实现4变量一致电路。

（2）四变量的多数表决电路解：（1）1）定变量列真值表：ABCDYABCDY0000110000000101001000100101000011010110010*******010*******011001110001110111112）列函数表达式：YABCDABC D ABCDABCD3）用与非门组电路（2）输入变量A、B、C、D，有3个或3个以上为1时输出为1，输人为其他状态时输出为0。

1）列真值表2）些表达式3）用与非门组电路4．有一水箱由大、小两台水泵ML和Ms供水，如图所示。

水箱中设置了3个水位检测元件A、B、C，如图（a）所示。

水面低于检测元件时，检测元件给出高电平；水面高于检测元件时，检测元件给出低电平。

现要求当水位超过C点时水泵停止工作；水位低于C点而高于B点时Ms单独工作；水位低于B点而高于A点时ML单独工作；水位低于A点时ML和Ms同时工作。

试用门电路设计一个控制两台水泵的逻辑电路，要求电路尽量简单。

解：（1）根据要求列真值表（b）（b）（a）（2）真值表中×对应的输入项为约束项，利用卡诺图化简（c）（d）（c）（d）（e）得：MABCsMBL（ML、M S的1状态表示工作，0状态表示停止）（3）画逻辑图（e）5．某医院有—、二、三、四号病室4间，每室设有呼叫按钮，同时在护士值班室内对应地装有一号、二号、三号、四号4个指示灯。

第5章三相电路一、填空题：1. 对称三相负载作Y接，接在380V的三相四线制电源上。

此时负载端的相电压等于倍的线电压；相电流等于倍的线电流；中线电流等于。

2. 有一对称三相负载接成星形联接，每相阻抗模均为22Ω，功率因数为0.8，又测出负载中的电流为10A，那么三相电路的有功功率为；无功功率为；视在功率为。

假如负载为感性设备，则等效电阻是；等效电感量为。

3. 三相对称电压是指频率、幅值、相位互差的三相交流电压，三相对称电压的瞬时值之和等于。

4. 在三相对称负载三角形连接的电路中，线电压为220V，每相电阻均为110Ω，则相电流I P=___ ____，线电流I L=___ __。

线电流比相应的相电流。

5.对称三相电路Y形连接，若相电压为()οV，则线电压ω60=tu220-sinA=u V。

AB6.三相四线制供电方式，中线的作用是使星形连接的不对称负载的对称，中线上不许接、。

7.三相电路星形连接，各相电阻性负载不对称，测得I A =2A,I B =4A,I C=4A，则中线上的电流为。

8．在三相正序电源中，若B相电压u B初相角为-90º，则线电压u AB的初相角为；若线电压u AB初相角为45º，则相电压u A的初相角为。

9．当三相对称负载的额定电压等于三相电源的线电压时，则应将负载接成；当三相对称负载的额定电压等于三相电源的相电压时，则应将负载接成。

10．三相电源的线电压对应相电压30°，且线电压等于相电压的倍；三相对称负载作三角形连接时，线电流对应相电流30°，且线电流等于相电流的倍。

11．三相交流电路中，只要负载对称，无论作何联接，其有功功率为。

12. 三相电源线电压U l ＝380V ，对称负载阻抗为Z ＝40＋j30Ω，若接成Y 形，则线电流I l ＝______A ，负载吸收功率P ＝______W ；若接成Δ形，则线电流I l ＝______A ，负载吸收功率P ＝______W 。

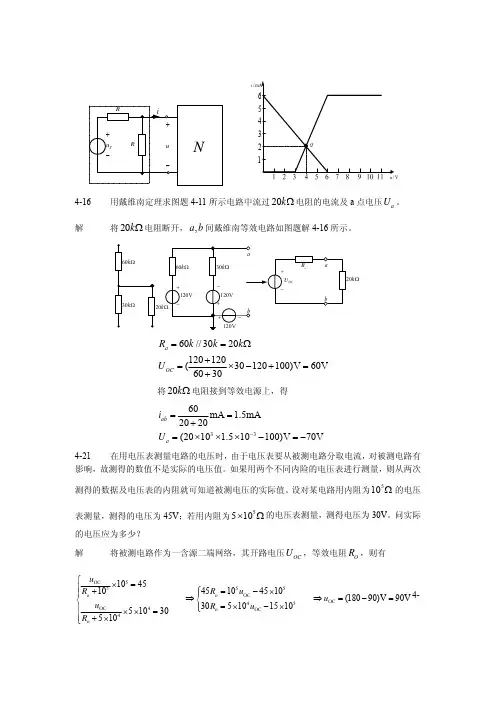
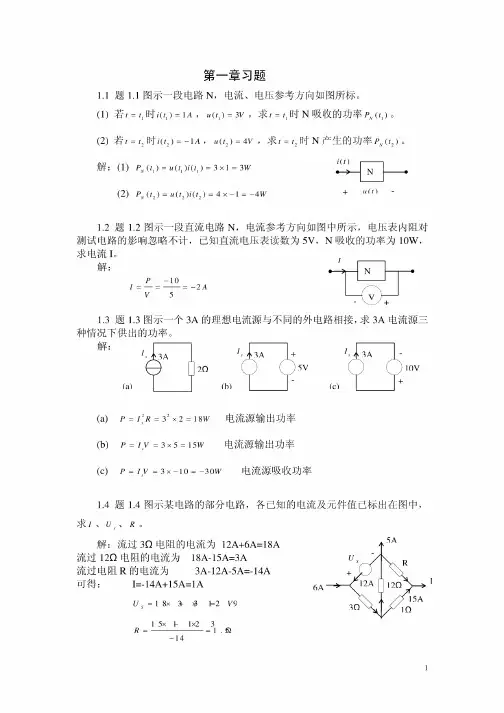
/i4-16 用戴维南定理求图题4-11所示电路中流过20k Ω电阻的电流及a 点电压。

a U 解将电阻断开，间戴维南等效电路如图题解4-16所示。

20k Ω,a bk Ω60//3020120120(30120100)V 60V6030a OCR k k k U ==Ω+=×−+=+ 将电阻接到等效电源上，得20k Ω3360mA 1.5mA2020(2010 1.510100)V 70V ab a i U −==+=×××−=− 4-21 在用电压表测量电路的电压时，由于电压表要从被测电路分取电流，对被测电路有影响，故测得的数值不是实际的电压值。

如果用两个不同内险的电压表进行测量，则从两次测得的数据及电压表的内阻就可知道被测电压的实际值。

设对某电路用内阻为的电压表测量，测得的电压为45V ；若用内阻为510Ω5510×Ω的电压表测量，测得电压为30V 。

问实际的电压应为多少？ 解将被测电路作为一含源二端网络，其开路电压，等效电阻OC U O R ，则有5OC 555o o OC OC 454OCo OC 4o 10451045104510(18090)V 90V 30510151051030510u R R u u u R u R ⎧×=⎪⎧+=−×⎪⎪⇒⇒=⎨⎨=×−×⎪⎪⎩××=⎪+×⎩−=4-28 求图题4-20所示电路的诺顿等效电路。

已知：12315,5,10,R R R =Ω=Ω=Ω。

10V,1A S S u i ==解对图题4-20所示电路，画出求短路电流和等效内阻的电路，如下图所示SC i对左图，因ab 间短路，故0,0i i α==，10A 0.5A 155SC i ==+ 对右图，由外加电源法，106ab R α=Ω− 4-30 电路如图题4-22所示。

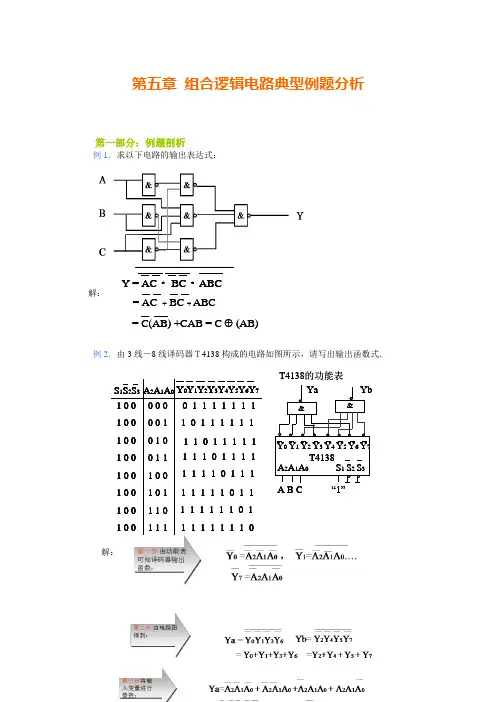
第五章 组合逻辑电路典型例题分析第一部分：例题剖析例1．求以下电路的输出表达式：解：例2．由3线－8线译码器Ｔ4138构成的电路如图所示，请写出输出函数式．解：Y = AC BC ABC= AC +BC + ABC = C(AB) +CAB = C (AB) T4138的功能表&&Y 0 Y 1 Y 2 Y 3 Y 4 Y 5 Y 6 Y 7“1”T4138A B CA 2A 1A 0YaYbS 1 S 2 S 30 0 00 0 10 1 00 1 11 0 01 0 11 1 01 1 1S 1S 2S 31 0 01 0 01 0 01 0 01 0 01 0 01 0 01 0 0A 2A 1A 0Y 0Y 1Y 2Y 3Y 4Y 5Y 6Y 70 1 1 1 1 1 1 11 0 1 1 1 1 1 11 1 0 1 1 1 1 11 1 1 0 1 1 1 11 1 1 1 0 1 1 11 1 1 1 1 0 1 11 1 1 1 1 1 0 11 1 1 1 1 1 1 0例3．分析如图电路，写出输出函数Ｚ的表达式。

CC4512为八选一数据选择器。

解：例4．某组合逻辑电路的真值表如下，试用最少数目的反相器和与非门实现电路。

（表中未出现的输入变量状态组合可作为约束项）CC4512的功能表A ⨯DIS INH 2A 1A 0Y1 ⨯0 10 00 00 00 00 00 00 00 0⨯⨯⨯⨯⨯0 0 00 0 10 1 00 1 11 0 0 1 0 11 1 01 1 1高阻态　0D 0D 1D 2D 3D 4D 5D 6D 7ZCC4512A 0A 1A 2D 0 D 1 D 2 D 3 D 4 D 5 D 6 D 7DIS INHD1DA B C D Y 0 0 0 0 10 0 0 1 00 0 1 0 10 0 1 1 00 1 0 0 0CD AB 00 01 11 1000 1 0 0 101 0 1 0 1 11 ××××10 0 1 ××AB第一步画卡诺图第三步画逻辑电路图例5．写出下面组合电路的输出表达式,分析逻辑功能。

CHAPTER 5P5.1. For each problem, restate each Boolean equation into a form such that it can be translatedinto the p and n-complex of a CMOS gate.a. ()()Out ABC BD ABC BD A B C B D =+=+=+++b. ()()()Out AB AC BC AB AC BC A B A C B C =++=++=+++c. ()()Out A B CD A AB C D A A B CD A A B CD A =+++=++=+++=++AbVddVddAb BbAAbVddP5.2.AP5.3. First, convert the equation into its p and n-complex.()()()()()()()()()()()Out A B C BC AB AB C BC AB AB C BC AB AB C BC AB AB C BC AB AB C B C =⊕+=++=++=+=++=+++VddP5.4. The truth table is given below in terms of voltages. The function is F A B =The worse case V OH is V DD and the worse case V OL is 0V.P5.5. The first circuit is a NOR gate while the second is a NAND gate. The V OL and V OHcalculated are for the worst-case scenario. To find this, assume only one transistor turns on, this just reduces to a pseudo-NMOS/PMOS inverter, so the other transistors are not important.a. The V OL for the pseudo-NMOS (in 0.18μm) is:()()()2,1N N OXNSAT OX P GSP TPP SATOL W C L N DD TN GSP TP CP PDD TN SAT P N OX v C W V V I V k V V V V E L V V v W L C μ-==--+-=()2DD TP N N OX V V W C μ-()()()()()20.1DD TP CP P DD TN SAT P N DD TPDDN N DD TP CP P DD TN V V E L V V v W L V V V W V V E L V V μ-+--==-+-()()()()()()()()()()()()226440.18100.2100.210 1.80.50.14μm=1.40.11.8270 1.80.5240.2 1.80.5SAT P N DD TPN DD N DD TP CP P DD TN v W L V V W V V V E L V V μλ---=-+-⨯⨯⨯-==-+-Since the minimum width is 2λ, we make that the width. The V OH for the pseudo-PMOS (in 0.18μm) is:()()()()()()2221SDPSDP CP PN P V P OX P SGP TP SDP SAT OX N GSN TN V GSN TN CN N N E L SAT OX I sat I lin C W V V V v C W V V V V E L L v C μ=---=-++()2P OX N DD TN DD TN CN NC W V V V V E L μ-=-+()()()()()()2201DD OH DD OH CP PV V P DD TPDDOH V V P E L W V V VV L ------+()()()()()()20.1824620.184.8(70) 1.80.50.180.2(10)(810)1.80.51.80.5 1.21P P W L ---⨯-=-++4.2P W λ≈The pseudo-PMOS circuit will have bigger devices than the pseudo-NMOS.P5.6. The steps to solving this question are the same as the pseudo-NMOS question in Chapter4.a. For V OH , recognize that GS T V V >= for operation so the output can only be as high asDD T V V -. Since 0SB V ≠, body effect must be taken into account and the full equationis:()()()001.20.40.2OH DD T DDT V V V V Vγγ=-+=-+=-+ Iteration produces V OH =0.73V.b. For V OL , we must first recognize that the worst-case V OL occurs when only one of the pull-down transistors is on. Next we identify the regions of operation of the transistors. In this case, the pull-up transistor is always in saturation and the pull-down is most likely in the linear region since it will have a high input (high V GS ) and a low output (low V DS ). Then, we equate the two currents together and solve for V OL :()()()()()()()()221222222211111224620.61(1)(270)1.20.4(0.13)(10)(810)1.20.42(1.20.42)0.61DS DS CN OL OLV N OX GS T DS sat OX GS T V GS T CN E LV OL OL V OL I sat I lin W C V V V W v C V V V V E LL V V V μ-=---=-++--⨯--=--++Using a programmable calculator or a spreadsheet program, V OL = 0.205V. The dc current with the output low is:()()()()2222222260.20520.2050.61(1)(270)(1.610)1.20.4(0.205)146.5DS DS CN V N OX GS T DS DS V ELW C V V V I L Aμμ---=+⨯--=+=The power with the output low is:(46.5)(1.2)55.8DS DD P I V A V W μμ===P5.7. See Example 5.2 which is based on the NAND gate. This question is the same except thatit addresses the NOR gate.With both inputs tied together, 88N P W W λλ==2χ=== ()()1.80.520.50.77V 112DD TP TNS V V V V χχ-+-+===++In the SPICE solution, the reason why the results vary for input A and B is due to body-effect.P5.8. The solution is shown below. Notice that there is no relevance with the lengths andwidths of the transistors when it comes to V OH , although they the do matter when calculating V OL.01.80.50.3 2.51Vout GG T GG out T V V V V V V γ=-=++=++=P5.9. For t PLH , we need to size the pull-up PMOS appropriately.()()()()15120.70.720.70.73010010845010PLH eqp LOAD p SQLOAD PLHLt RC R C WL W R C k t λλ--====Ω⨯=⨯For V OL :()()()()()()()()()()()()()2246660.1220.10.63 4.210810 1.610 1.20.4 1.08mA1.20.4240.1(270)(1.610)1.20.40.11138.577377232(3OLOL CN P sat OX GS T P GS T CP V N N OX OL TN OLN P V N N E LNN NW v C V V I sat V V E LW C V V V W I sat L L W W W stack L μλλλ---⨯⨯⨯--===-+-+--⨯--==++===⨯=2)155(2)W stack λ=P5.10. The circuit is shown below:()()()()()()()()31512315120.720.70.7301075106350100.720.70.712.510751026.6275010PLH EQP LOAD PP EQPLOAD PLHPHL EQN LOAD NN EQNLOAD PHLLt RC R C W L W R C t Lt RC R C W L W R C t λλλλλ----====⨯⨯=⨯====⨯⨯=≈⨯Because the number of transistors in series is more than one, we must multiply the widths by the appropriate number. Here, all the NMOS transistors will have a width of 54λ. The PMOS transistors will have widths of 126λ and 190λ, respectively.P5.11. We estimate the dc power and dynamic switching power for this problem.a. The circuit’s dc power can be computed by computing the dc current when the output is low. This is given by I DS =550uA/um x 0.1um=55uA. Then P DC =66uW when the output is low.b. Its dynamic power can be calculated by simply using the equation 2dyn DD P CV f α=. Therefore, P dyn =(50fF)(V DD -V TN )(V DD )(100MHz)=4.4uW.P5.12. The pseudo-NMOS inverter has static current when the output is low. We can estimate itas:()()()()()()()()224660.110810 1.610 1.20.425.6A 1.20.4240.1P sat OX GS T P GS T CP W v C V V I sat V V E Lμ--⨯⨯⨯--===-+-+Then the average static power is P stat =(25.6uA)(1.2)/2 =15.4uW.The dynamic power is dyn DD swing avg P CV V f ==(50fF)(1.2)(1.1)f avg assuming that V OL is 0.1V.For the CMOS inverter, the static power is almost zero: P stat =I sub V DD . It is far less than the pseudo-NMOS case. The dynamic power dyn DD swing avg P CV V f ==(50fF)(1.2)2f avg is slightly larger than the pseudo-NMOS case.VVINCMOS InverterV V INPseudo-NMOSP5.13. Model development to compute αsc .P5.14. The energy delivered by the voltage source is:()()200202DDDDV C sourceDD DD L L DDCL DDV CDDcap C LC L C C LdvE i t V dt V C dt C V dvC V dt dv V E i t v dt C v dt C v dv C dt∞∞∞∞========⎰⎰⎰⎰⎰⎰As can be seen, only half the energy is stored in the capacitor. The other half was dissipated as heat through the resistor.P5.15. The average dynamic power does not depend on temperature if the frequency stays thesame. However, the short-circuit current will increase as temperature increases. In addition, the subthreshold current increases as temperature increases. So the overall power dissipation will be higher. P5.16. The circuit is shown below. The delay should incorporate both Q and Qb settling in400ps. All NMOS and PMOS devices are the same size in both NAND gates.QQW()()()()()()()()15331220.70.70.70.720.71001030100.1212.5100.10.72400101μm N P P PHL PLH UP LOAD DOWN LOAD LOAD eqp eqn P N LOAD eqp eqn LOAD eqp eqn PL Lt t t R C R C C R R W W C R L R L WC R L R L W t --⎛⎫=+=+=+ ⎪⎝⎭+=++==≈P5.17. The small glitch in J propagates through the flop even though it is small. This is due tothe fact that the JK-flop of Figure 5.20 has the 1’s catching problem. P5.18. The small glitch in J does not propagate through the flop since the edge-triggeredconfiguration does not have a 1’s catching problem.P5.19. The positive-edge triggered FF is as follows:QQDS(a) With CK=D=0 and S=R=1, the outputs are(b) Now CK=0。

电路分析基础[第五章动态电路的分析]课程复习第五章动态电路的分析5．2．1 动态电路初始条件的确⽴⼀、初始条件动态电路中，⼀般将换路时刻记为t=0，换路前的⼀瞬间记为t=0_，换路后的⼀瞬间记为t=0+，则电路变量在t=0+的值，称为初始值，也称初始条件。

⼆、换路定则如果在换路前后，电容电流或电感电压为有限值，则换路时刻电容电压和电感电流不跃变，即uC (0_)=uC(0+)，iL(0_)=iL(0+)。

三、初始条件的计算(1)由换路前最终时刻即t=0_时的电路，求出电路的独⽴状态变量uC(0_)和iL (0_)。

从⽽根据换路定则得到uC(0+)和iL(0+)；(2)画出t=0+时的等效电路。

在这⼀等效电路中，将电容⽤电压为uC(0+)的直流电压源代替，将电感⽤电流为iL(0+)的直流电流源代替；(3)由上述等效电路，⽤直流电路分析⽅法，求其他⾮状态变量的各初始值。

5．2．2 动态电路的时域分析法5．2．2．1⼀阶电路的响应⼀阶电路是指只含有⼀个独⽴储能元件的动态电路。

⼀、⼀阶电路的零输⼊响应零输⼊响应是指动态电路⽆输⼊激励情况下，仅由动态元件初始储能所产⽣的响应，它取决于电路的初始状态和电路的特性。

因此在求解这⼀响应时，⾸先必须掌握电容电压或电感电流的初始值，⾄于电路的特性，对⼀阶电路来说，则是通过时间常数τ来体现的。

零输⼊响应都是随时间按指数规律衰减的，这是因为在没有外施激励的条件下，原有的储能总是要衰减到零的。

在RC电路中，电容电压总是从uC (0+)单调地衰减到零的，其时间常数τ=RC，即uC(t)=uC(0+)e-t/τ；在RL电路中电感电流总是从iL，(0+)单调地衰减到零的，其时间常数τ=L／R，即iL (t)=iL(0+)e-t/τ，掌握了uC(t)和iL(t)后，就可以⽤置换定理将电容⽤电压值为uC (t)的电压源置换，将电感⽤电流值为iL(t)的电流源置换，再求电路中其他⽀路的电压或电流即可。

第五章 正弦稳态电路分析习题解答5-1 已知正弦电流)60314cos(20 +=t i A ，电压)30314sin(210-=t u V 。

试分别画出它们的波形图，求出它们的有效值、频率及相位差。

解 电压u 可改写为)120314cos(210)30314sin(210 -=-=t t u Vi 、u 波形图如图所示。

其有效值为V 10142.14220=A==U I i 、u 的频率为Hz 5014.32314π2=⨯==ωfu 、i 的相位差为18060120-=--=-= ψψϕi u5-2 己知)3πcos(m +=t Ιi ω，当s 5001=t 时，第一次出现零值，求电流频率f 。

解 按题意有题5-1图0)3π500cos(m =+=ωI 2π3π500=+ω 得)3π2π(500-=ωHz 667.41)3π2π(2π500π2=-==ωf5－3 在图示相量图中，己知A 101=I ，A 52=I ，V 110=U ，Hz 50=f ，试分别写出它们的相量表达式和瞬时值表达式。

解 相量表达式为V0110A 455A 301021 ∠=∠=-∠=∙∙∙U I I瞬时值表达式为A )30314cos(2101 -=t i A )45314cos(252 +=t iV )314cos(2110t u =5－4 己知某正弦电压V )π100sin(10ψ+=t u ，当s 3001=t 时，V 5)(3001=u ，题5－3图 ∙U ∙则该正弦电压的有效值相量=∙U？解 按题意有5)300π100sin(10=+ψ求出6π300π100)105arcsin(-=-=ψ 故V 6π256π210-∠=-∠=∙U5－5 实际电感线圈可以用R 、L 串联电路等效，现有一线圈接在56V 直流电源上时，电流为7A ；将它改接于50Hz 、220V 的交流电源上时，电流为22A 。

试求线圈的电阻和电感。

第五章 时序逻辑电路 习题解答注：1. 用EDA 软件(例如Multisim ／EWB)可以帮助解题。

凡加注了“★”的题，可以用用该类软件求解；凡加注了“◆”的题，以用该类软件进行验证。

2. 答案仅供参考，且非唯一。

也不一定是最佳答案。

[题 5.1] 分析图P5.1时序电路的逻辑功能，写出电路的驱动方程、状态方程和输出方程，画出电路的状态转换图，说明电路能否自启动。

[解]11322131233n 113131n 1212212n 133213311;J K Q J K Q J Q Q K Q Q Q Q Q Q QQ Q Q Q Q Q Q Q Q Q Q Q Y Q +++=======+==+=⊕==电路能自启动。

状态转换图如图A5.1。

[题 5.2] 试分析图P5.2时序电路的逻辑功能，写出电路的驱动方程、状态方程和输出方程，画出电路的状态转换图。

A 为输入逻辑变量。

[解]12212+12n 112n 1212 ()(+)D A Q D A Q Q A Q Q QAQ Q A Q Q ++===== 21=Y A Q Q电路的状态转换图如图A5.2。

[题 5.3] 试分析图P5.3时序电路的逻辑功能，写出电路的驱动方程、状态方程和输出方程，画出电路的状态转换图，检查电路能否自启动。

[解]12312121331232n 11231n 12123132n+13123223;1 ; ;=J Q Q K J Q K Q Q J Q Q K Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Y Q Q ++=======+=+= 电路的状态转换图如图A5.3。

电路能自启动。

[题 5.4] 分析图P5.4给出的时序电路，画出电路的状态转换图，检查电路能否自启动，说明电路实现的功能。

A 为输入变量。

[解]n+11111n 122221212121=+J K Q Q J K A Q Q A Q Q Y A Q Q A Q Q +=====⊕=⊕⊕电路状态转换图如图A5.4。