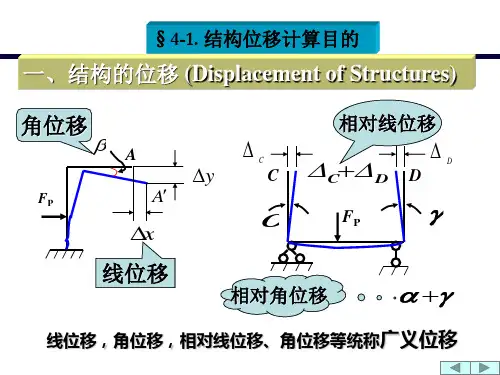
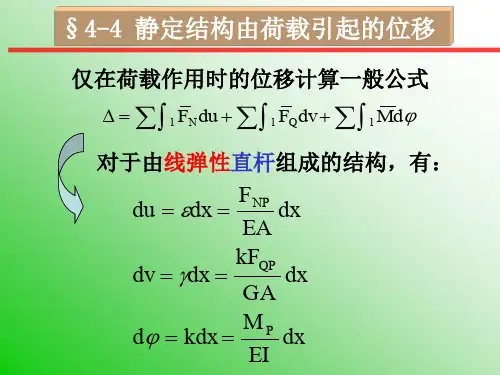
注:无支座移动
例 1:已知图示粱的E 、G,
q
求A点的竖向位移。
解:构造虚设单位力状态.
N k(x)0,NP(x)0
Ah
l
b
Q k(x) 1 ,Q P (x) q (l x) M k (x ) x l,M P (x ) q ( l x ) 2 /2M P
P1 x
q
ip0[l[N qE P (N lG iA x)A Q G P Q qiA ( l2 M EE xP )M I3]iId]dxs设:MM i Q8qEP4lPI,Q1q2Gl2A
反之,取负值。
3. 如图形较复杂,可分解为简单图形.
三、应用举例
例 1. 已知 EI 为常数,求A、B两点相对水平位移 。 AB
平衡方程 几何方程
第一种应用一些文献称为“虚位移原理”, 而将第二种应用称为“虚力原理”。
虚位移原理:一个力系平衡的充分必要条件是:对 任意协调位移,虚功方程成立。 虚力原理:一个位移是协调的充分必要条件是:对 任意平衡力系,虚功方程成立”。
§4-4. 单位荷载法
一.单位荷载法
k
求k点竖向位移.
iP
故有Wex = Ude成立。
几个问题:
1. 虚功原理里存在两个状态: 力状态必须满足平衡条件;位移状态必须满足协调
条件。
2. 原理的证明表明:原理适用于任何 (线性和非线性)的 变形体,适用于任何结构。
3. 原理可有两种应用: 实际待分析的平衡力状态,虚设的协调位移状态,
将平衡问题化为几何问题来求解。 实际待分析的协调位移状态,虚设的平衡力状态,
由 MB0求得: YAb/a
虚功方程为: 1YAc0
解得:
bc/a