结构力学在线测试第四章复习课程

第一章测试1.结构必须由刚性构件组成，索、膜等柔性构件不能作为结构的一部分。

（）A:错B:对答案:A2.结构力学的主要任务是计算内力和位移，定性分析不属于本课程的内容。

（）A:对B:错答案:B3.关于定向活动支座的作用，以下说法完全正确的是（）。

A:可等效为1个支座反力B:可等效为1个支座反力，且约束1个方向的位移C:可等效为1个反力和1个反力矩，且约束1个方向线位移和一个角位移D:可等效为2个支座反力答案:C4.关于活动铰支座的作用，以下说法完全正确的是（）。

A:可等效为1个支座反力B:可等效为2个支座反力，且约束2个方向的位移C:可等效为2个支座反力D:可等效为1个支座反力，且约束1个方向的位移答案:D5.平面杆系结构的计算简图应包含哪些内容（）。

A:约束B:支座C:外荷载D:杆件答案:ABCD第二章测试1.图中可视为几何不变体系的有（）。

A:B:C:D:答案:ABC2.以下选项图中可视为几何不变体系的有（）。

A:B:C:D:答案:AC3.图示各体系，关于刚片间的连接说法正确的是（）。

A:图1中两个刚片通过铰A连接B:图2中刚片III和刚片I，II通过铰A连接C:图1中两个刚片通过铰A连接，图2中刚片III和刚片I，II通过铰A连接，图3中三刚片通过3个铰两两连接都不正确D:图3中三刚片通过3个铰两两连接答案:C4.以上图示体系的几何组成应为（）。

A:几何不变体系，有多余约束B:几何不变体系，无多余约束C:瞬变体系D:几何可变体系答案:B5.上述图片体系的几何组成应该为（）。

A:几何不变体系，无多余约束B:几何不变体系，有多余约束C:瞬变体系D:几何可变体系答案:C6.以上图示体系的几何组成应该为（）。

A:几何可变体系B:瞬变体系C:几何不变体系，无多余约束D:几何不变体系，有多余约束答案:B7.1个虚铰和1个单铰都能起到2个约束作用。

（）A:对B:错答案:A8.图示两个体系均为几何不变体系。

恭喜，交卷操作成功完成！你本次进行的《结构力学》第04章在线测试的得分为20分（满分20分），本次成绩已入库。

若对成绩不满意，可重新再测，取最高分。

测试结果如下：
∙ 1.1 [单选] [对] 悬臂梁固定端截面的弯矩影响线的最大竖标在
∙ 1.2 [单选] [对] 悬臂梁固定端截面的剪力影响线
∙ 1.3 [单选] [对] 简支梁的弯矩影响线是
∙ 1.4 [单选] [对] 简支梁AB，跨度为6m，C为跨间一截面，AC长为2m，则C截面弯矩影响线中的最大竖标是
∙ 1.5 [单选] [对] 外伸梁支座反力影响线形状特征是
∙ 2.1 [多选] [对] 外伸梁伸臂上的截面剪力影响线是
∙ 2.2 [多选] [对] 下列哪些量值的影响线是无量纲的？
∙ 2.3 [多选] [对] 下列哪些量值的影响线是长度量纲？
∙ 2.4 [多选] [对] 伸臂梁的影响线的特点是
∙ 2.5 [多选] [对] 下列关于影响线的论述正确的是
∙ 3.1 [判断] [对] 静定结构的内力和反力影响线是直线或折线组成。

∙ 3.2 [判断] [对] 若有一集中力作用在影响线顶点，必为荷载临界位置。

∙ 3.3 [判断] [对] 悬臂梁固定端截面的弯矩影响线的最大竖标（绝对值）在自由端截面。

∙ 3.4 [判断] [对] 静定结构基本部分上的某量值的影响线在附属部分上的影响线竖标为零。

∙ 3.5 [判断] [对] 简支梁的反力影响线是一条直线。

同济大学朱慈勉结构力学第4章习题答案（1）4-5 试用静力法作图示结构中指定量值的影响线。

(a)MA 0 知1 5d F 7d 1 ( 5d x)RBx xF ,FRB QDB7d7dx,(0 x 2d)M ( CD )以右侧受拉为正DC2d, (2d x 5d)C C2d D5/7 AAF M DCQDB(b)以为坐标原点，向右为x 轴正方向。

弯矩M 以右侧受拉为正A当0 x a 时，MFx0 F 1 ( )RAa分析以右部分，GCD 为附属部分，可不考虑Fx/aM xEFB GFNEE x aFp=1当 a x 3 a 时，去掉AF,GCD 附属部分结构, 分析中间部分F GB M =(2a-x),FE NE1E4-x/aF BGE 当 3 a x 4 a 时，由M 0 知Gx 3 a xxM =x-4a,F3 , F4 ERD NEa aaa1 1A ACF G BBCF GaM 的影响线 F NE 的影响线E(c)1A B C D E F32 2m1G H I J K110 ×2m上承荷载时：以 A 点为坐标原点，向右为x 轴正方向。

F =1-RA当0 x 8( C 点以左) 时，取1-1 截面左侧考虑x20( )由MIx x 0 F [(10 x x ) (1 ) 10] / 2N320 4当12 x 20( D 点以右) 时，由MIx(1 ) 1020x0 F 5N32 4F CD C D在之间的影响线用点及的值。

直线相连。

N3当0 x 8 时，取1-1 截面左侧分析由 F 由 F yxx 20 1 F sin 45 1 知 F 2xN2 N220 20x0 F F F cos 45 4N1 3 N25A B C D E FFN3FN2FN1(d)M 0 1 (8 d x ) F 8 d F 1B RA RA 8 x dF F 1 FRA RB RB 8 x d上承荷载时2 5当时，取截面右侧分析。

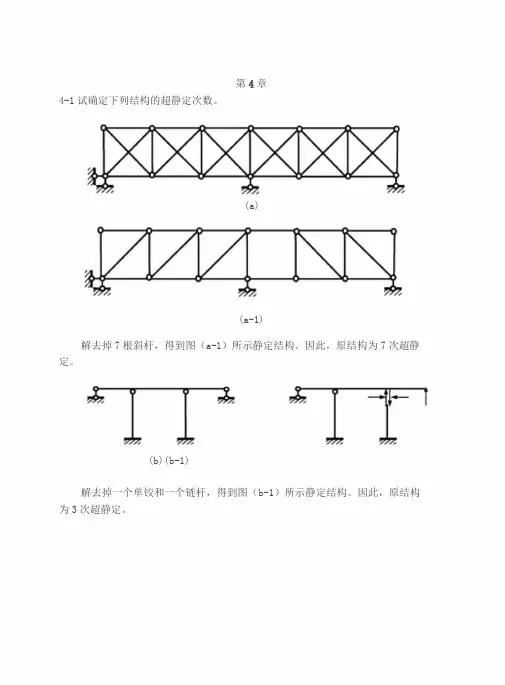
第4章4-1试确定下列结构的超静定次数。

(a)(a-1)解去掉7根斜杆，得到图（a-1）所示静定结构。

因此，原结构为7次超静定。

(b)(b-1)解去掉一个单铰和一个链杆，得到图（b-1）所示静定结构。

因此，原结构为3次超静定。

(c)(c-1)解去掉三个水平链杆，得到图（c-1）所示静定结构。

因此，原结构为3次超静定。

(d)(d-1)解去掉两个单铰，得到图（d-1）所示静定结构。

因此，原结构为4次超静定。

(e)(e-1)解去掉两个单铰，切断一个梁式杆，得到图（e-1）所示静定结构。

因此，原结构为7次超静定。

(f)(f-1)解去掉四个支链杆，切断两个梁式杆，得到图（f-1）所示静定结构。

因此，原结构为10次超静定。

(g)(g-1)解去掉一个单铰，两个链杆，切开一个封闭框，得到图（g-1）所示静定结构。

因此，原结构为7次超静定。

(h)(h-1)解切开七个封闭框，得到图（g-1）所示静定结构。

因此，原结构为21次超静定。

(i)(i-1) 解切开两个封闭框，得到图（i-1）所示静定结构。

因此，原结构为6次超静定。

4-2试用力法计算下列超静定梁，并作M和F Q图。

EI为常数。

qqAl(a) B A BX1基本体系A BX11lM图1ql2/22/2q l2/82/8q l2/82/8BABM P图M图解11X11P034lql3qlX 111P13EI8EI84-2(b)FP X1X2F PAABBl/2l/2基本体系11A ABX11X21 BM图1 M图2F P F Pl/8FPl/8 AABBF P l/4 M P图F P l/8 M图解XX 1111221P 0XX2112222P2 llFlP，，11223122161P2P16EIEIEIFlPXX1284-2(c)F PFP1Al（c）B A基本体系BX1M图1BX1=1F P lF P l/2FPB ABAM P图F P l/2M图解11X11P0；2lFlP、；111PEI2EIFlPX。

结构力学 第四章习题 参考答案2005级4－1 图示抛物线拱的轴线方程24(fy x l l=−)x ，试求截面K 的内力。

解：（1） 求支座反力801155 kN 16AV AV F F ×=== 0805(5580)0.351500.93625 kN 16BV BV F F ×==−×+×== 0Mc 55880350 kN 4H F f ×−×===（2） 把及代入拱轴方程有:16m l =4m f =(16)16xy =−x （1）由此可得:(8)tan '8x y θ−==（2） 把截面K 的横坐标 ,代入（1），（2）两式可求得: 5m x ==＞, 3.44m y =tan 0.375θ= 由此可得:20.56θ= 则有sin 0.351θ=,cos 0.936θ=最后得出截面k 处的内力为: (上标L 表示截面K 在作用力左边，R 则表示截面在作用力右边)055550 3.44103 kN m K H M M F y =−=×−×=i0cos sin 550.936500.35133.93 kN L sK s H F F F θθ=−=×−×= (5580)0.936500.35140.95 kN R sK F =−×−×==40.95 KN 0sin cos 550.351500.93666.1 kN L NK s H F F F θθ=+=×+×= (5580)0.351500.93638.03 kN R NK F =−×+×=4－2 试求拉杆的半圆三铰拱截面K 的内力。

解：（1）以水平方向为X 轴,竖直方向为Y 轴取直角坐标系，可得K 点的坐标为：2m6mK K x y =⎧⎪⎨==⎪⎩ （2）三铰拱整体分别对A ，B 两点取矩，由平衡方程可解得支座反力：0 20210500 20210500 2100A By B Ay x Ax M F M F F F ⎧=×−××⎪⎪=×+××⎨⎪=−×=⎪⎩∑∑∑=== =＞ 5 kN ()20 kN () 5 kN ()Ay Ax By F F F =−⎧⎪=−⎨⎪=⎩向下向上向左（3）把拱的右半部分隔离，对中间铰取矩，列平衡方程可求得横拉杆轴力为：CN 0 105100MF =×−×∑=＞N 5 kN F =（4）去如图所示的α角，则有：=＞cos 0.6sin 0.8θθ=⎧⎨=⎩于是可得出K 截面的内力，其中：22(6)206525644 kN m 2K M ×=−+×−×−×=isK F (20265)sin 5cos 0.6 kN θθ=−×−×−×=− NK F (20265)cos 5sin 5.8 kN θθ=−−×−×−×=−13K M F r Fr ==（内侧受拉） K 截面作用有力，剪力有突变 且有01sin3032LSK 2F F F F =−=−×=− （2） 22R SK F FF F =−=（3）011sin30(326NKF F F F ==×=拉力）（4）4-4 试求图示三铰拱在均布荷载作用下的合理拱轴线方程。

第四章 力法4-1 利用对称与反对称条件，简化图4-15所示各平面刚架结构，要求画出简化图及其位移边界条件。

P P(a)(a)解：对称结构，在对称载荷作用下，在对称轴上反对称内力为零。

由静力平衡条件∑=0X可得23P N =再由两个静力平衡条件，剩余4个未知力，为二次静不定。

本题中通过对称性条件的使用，将6次静不定的问题转化为2次静不定。

1PP(b)(b)解：对称结构，在反对称载荷作用下，在对称轴上对称的内力为零。

受力分析如图所示有2根对称轴，结合平衡方程，剩下三个未知数，为3次静不定。

本题中通过对称性条件的使用，将6次静不定问题转化为3次静不定。

(c)(c)解：对称结构，在对称载荷作用下，在对称轴上反对称内力为零。

有一根对称轴，减少了两个静不定度本题中通过对称性条件的使用，将3次静不定问题转化为1次静不定。

4-2图4-16所示桁架各杆的EA均相同，求桁架各杆的内力。

(a)(a)解：1、分析结构静不定次数。

结构有4个结点8个自由度，6根杆6个约束，3个外部约束。

因此结构静不定次数为1，f=1。

2、取基本状态。

切开2-4杆，取<P>,<1>状态，各杆内力如图。

1234P-P √2P<P>1234P<1>11√22√22√22√22计算影响系数∑=∆EAl N N i p P 11()2422222+=⎪⎪⎭⎫ ⎝⎛⨯+⨯=EA Pa P P EA a ∑=EAl N i1211δ()22222142222+=⎪⎪⎭⎫ ⎝⎛⨯⨯+⨯⨯=EA a EA a 列正则方程：()()02242221=+++P X解之()P X 42321-=3、由11N X N N P +=，得()P X N 423220112-=⎪⎪⎭⎫ ⎝⎛-⋅+= ()P X P N 42212113+=⋅+=()P X N 423220114-=⎪⎪⎭⎫ ⎝⎛-⋅+=()P X N 423220123-=⎪⎪⎭⎫ ⎝⎛-⋅+=()P X N 423210124-=⋅+=()P X P N 42122134+-=⎪⎪⎭⎫ ⎝⎛-⋅+-=4、校核。

《结构力学》第04章在线测试A BC DA BC DA BC DA BC DA BC DE、a为P＝1在C右时产生的C截面剪力2、外伸梁伸臂上的截面剪力影响线是A、在该截面以外是一条斜直线B、在该截面以里是一条斜直线C、在该截面以里是零线D、在该截面以外是一条水平线E、在该截面以里是一条水平线3、外伸梁支座间的截面剪力影响线是A、两条直线组成的折线B、一条直线C、抛物线D、在支座处竖标为零E、两条平行线4、外伸梁支座处截面弯矩影响线的形状特点是A、在该支座处竖标为零B、该支座以外是一条直线C、该支座以里是零线D、另支座处竖标为零E、一条直线5、下列哪些量值的影响线是无量纲的？A、支座反力B、剪力C、弯矩D、约束力矩正确错误正确错误、荷载的临界位置必然有一集中力作用在影响线顶点。

正确错误正确错误正确错误《结构力学》第05章在线测试A BC DA BC DA BC DA BC DA BC DE、弯矩2、温度变化对静定结构会产生A、位移B、变形C、轴力和剪力D、弯矩E、支座反力3、温度变化对静定结构不会产生A、位移B、变形C、轴力和剪力D、支座反力E、弯矩4、两个简支梁的跨度、荷载、截面尺寸相同但所用材料不同，则两者相同的因素是A、内力B、反力C、应力D、位移E、变形5、主从结构，仅附属部分温度升高，下列论述正确的是A、整个结构不产生内力B、整个结构产生变形C、附属部分发生变形D、基本部分上的位移为零正确错误正确错误、虚功是一种虚构的功，实际上是不可能存在的。

正确错误正确错误正确错误《结构力学》第06章在线测试A BC DA BC DA BC DA BC DA BDCD、轴力为零E、角位移为零2、两跨对称结构在对称荷载作用下，下列论述正确的是A、对称轴上的刚结点线位移为零B、对称轴上的刚结点角位移为零C、中柱无弯矩D、中柱无剪力E、中柱无轴力3、两跨对称结构在反对称荷载作用下，下列论述正确的是A、对称轴上的刚结点竖向线位移为零B、对称轴上的刚结点角位移为零C、中柱无弯矩D、中柱无剪力E、中柱无轴力4、在力法典型方程中可正可负可为零的是A、δ11B、δ12C、δ21D、δ22E、Δ1P5、求超静定结构的位移时，可将虚拟单位荷载加在A、任意静定的基本体系上B、原结构上C、几何可变体系正确错误正确错误正确错误正确错误正确错误《结构力学》第07章在线测试A BC DA BC DA BC DA BC DA BC DE、支座反力2、两跨对称结构在对称荷载作用下，下列论述正确的是A、对称轴上的刚结点线位移为零B、对称轴上的刚结点角位移为零C、中柱无弯矩D、中柱无剪力E、中柱无轴力3、下列哪些位移可以不作为位移法的基本未知量是A、铰结点处的转角B、铰支座处的转角C、滑动支座处的侧移D、刚结点的转动E、刚结点的线位移4、形常数指的是单跨超静定梁在A、杆端位移作用下产生的杆端弯矩B、杆端位移作用下产生的杆端剪力C、单位杆端位移作用下产生的杆端弯矩D、单位杆端位移作用下产生的杆端剪力E、跨间荷载作用下产生的杆端弯矩5、求超静定结构的位移时，可将虚拟单位荷载加在A、任意静定的基本体系上B、原结构上C、几何可变体系D、几何常变体系正确错误正确错误、位移法不能计算静定结构。

静定结构的位移计算习题4—1 (a)用单位荷载法求图示结构B 点的水平位移解：1. 设置虚拟状态选取坐标如图。

2. M P 图和 如图示3. 虚拟状态中各杆弯矩方程为实际状态中各杆弯矩方程为M P =F P x4. 代入公式（4—6）得 △BH =l实际状态1虚拟状态5F P l 15l M P 图图M 图M xM =141012118111EI F EI x F x EI x F x EI dx M M P l l P l P P =⨯⨯+⨯⨯=∑⎰⎰⎰(←)4—1 (b)单位荷载法求图示刚架B 点的水平位移 解：1. 设置虚拟状态选取坐标如图。

2. M P 图和 如图示3. 虚拟状态中各杆弯矩方程为 BD: DC: CA: 实际状态中各杆弯矩方程为 BD: M P =0 DC: M P =40x CA: M P =160+5x 24. 代入公式（4—6）得图M x M =3=M xM-=3△BH =4—2试求图示桁架结点B 的竖向位移，已知桁架各杆的EA =21×104KN 。

1M P 图M 3KN •m340KN •m3KN •m3KN •m)(833.05160)3(40306012401301←=+⨯-+⨯+*=∑⎰⎰⎰⎰cm EI x x x EI x EI x EI dxM M P实际状态虚拟状态解：虚拟状态如图示。

实际状态和虚拟状态所产生的杆件内力均列在表4—1中，根据式4—7可得结点B的竖向位移为表4—1中)(768.010215.16124↓=⨯∙=∆cm KNm KN BV4—3 （a）、（b）试用图乘法求图示结构B 处的转角和C 处的竖向位移。

EI=常数。

M=ql 2M P 图ql 2/81M=1（a ）解：M P 图、单位力偶下作用于B 点的1M 图、单位力下作用于C 点的2M 图EIql ql l ql l EI B 3)21223232221(1222=⨯⨯⨯-⨯⨯⨯=ϕ（ ）（b ）解：M P 图、单位力偶下作用于B 点的1M 图、单位力作用于C 点的2M 图)2183232421(122⨯⨯⨯-⨯⨯⨯=ql l l ql EI B ϕ=ql 3/24EI( ))23242212832232421(1222ql ql l ql ql l ql l ql EI cv ⨯⨯⨯⨯+⨯⨯⨯-⨯⨯⨯⨯=∆)(24)2852232322213221(14222↑-=⨯⨯⨯⨯⨯+⨯⨯⨯-⨯⨯⨯-=∆EI qll ql l ql l l ql l l EI CV= ql4/24EI(↓)（b）ql/2ql2/4l/2（C ）解：M P 图、单位力偶作用于B 点的1M 图、单位力作用于C 点时的2M 图EIl F lF ll EI P P B 12231211322121(12=⨯⨯⨯⨯+⨯⨯⨯⨯-=ϕ( )ll)(12231212232221(12↓=⨯⨯⨯⨯+⨯⨯⨯⨯⨯-=∆EIl F lF l l l F l l EI P P P cv 4—4 （a ）试求图示结构C 点的竖向位移。