(完整版)西北工业大学航空学院结构力学课后题答案第四章力法
- 格式:doc
- 大小:1.04 MB
- 文档页数:13



西工大飞行器结构力学课后答案第一题根据飞机结构力学的基本原理,飞机的结构力学可以被分解为静力学和动力学两个部分。
静力学是研究在静止或恒定速度下的力学行为,包括计算飞机各个部件的受力和应变情况。
而动力学则是研究在变化速度和加速度下的力学行为,包括计算飞机受到的各种动力荷载和振动情况。
第二题飞机的结构力学分析中,常用的方法包括有限元分析、静力学分析和动力学分析。
有限元分析是一种基于数值计算的方法,可以建立飞机结构的数学模型,并以此模型进行力学分析。
静力学分析是通过平衡方程来计算飞机结构的受力和应变情况,包括应力分析和变形分析。
动力学分析是通过力学方程来计算飞机在动态载荷下的振动响应和疲劳寿命。
第三题飞机的结构力学分析对于设计和制造过程中的决策具有重要意义。
在设计阶段,结构力学分析可以帮助工程师评估不同设计方案的有效性和可行性。
通过分析飞机的受力和应变情况,可以优化设计,并确保飞机在正常工作范围内具有足够的强度和刚度。
在制造阶段,结构力学分析可以帮助工程师确定合适的材料和加工工艺,以确保飞机结构的可靠性和安全性。
通过分析飞机的受力和应变情况,可以预测飞机在使用寿命内的疲劳寿命,并采取相应的措施延长飞机的使用寿命。
此外,结构力学分析还可以应用于飞机维修和事故调查过程中。
通过分析事故飞机的受力和应变情况,可以确定事故原因,并提出相应的维修和改进建议,以减少事故的发生对飞机结构的影响。
第四题对于飞行器结构力学的研究,需要掌握一些基本理论和方法。
首先是静力学的基本原理,包括力的平衡方程、应力和应变的定义和计算方法。
其次是动力学的基本原理,包括力的运动方程、振动的模型和计算方法。
此外,还需要了解一些基本的力学性能指标,如强度和刚度。
在进行结构力学分析时,需要掌握一些基本的计算方法。
常见的方法包括有限元法、解析法和试验法。
有限元法是一种基于数值计算的方法,可以建立飞机结构的数学模型,并以此模型进行力学分析。
解析法则是通过解析计算的方法进行力学分析,主要针对简单和规则的结构。

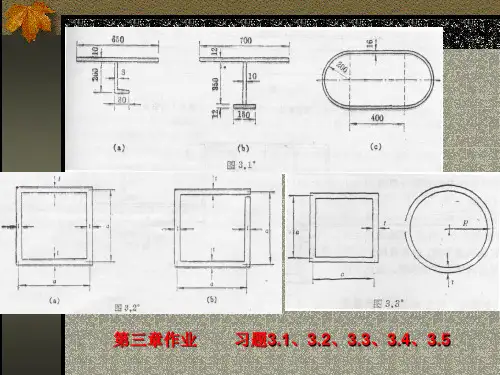
习题及参考答案【习题2】【习题3】【习题4】【习题5】【习题6】【习题8】【习题9】【习题10】【习题11】【习题12】【习题13】【习题14】【参考答案】习题22-1~2-14试对图示体系进行几何组成分析,如果是具有多余联系的几何不变体系,则应指出多余联系的数目。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图 题2-13图 题2-14图习题33-1 试作图示多跨静定梁的M 及Q 图。
(b)(a)20kN40kN20kN/m40kN题3-1图3-2 试不计算反力而绘出梁的M 图。
(b)5kN/m40kN(a)题3-2图习题44-1 作图示刚架的M 、Q 、N 图。
(c)(b)(a)20kN /m2kN /m题4-1图4-2 作图示刚架的M 图。
P(e)(d)(a)(b)(c)20k N /m4kN题4-2图4-3 作图示三铰刚架的M 图。
(b)(a)题4-3图4-4 作图示刚架的M 图。
(a)题4-4图4-5 已知结构的M 图,试绘出荷载。
(b)(a)题4-5图4-6 检查下列刚架的M 图,并予以改正。
(e)(g)(h)P(d)(c)(a)(b)(f)题4-6图习题55-1 图示抛物线三铰拱轴线方程x x l lfy )(42-=,试求D 截面的内力。
题5-1图5-2 带拉杆拱,拱轴线方程x x l lfy )(42-=,求截面K 的弯矩。
C题5-2图 题5-3图5-3 试求图示带拉杆的半圆三铰拱截面K 的内力。
习题66-1 判定图示桁架中的零杆。
(c)(b)题6-1图6-2 用结点法计算图示桁架中各杆内力。
(b)题6-2 图6-3 用截面法计算图示桁架中指定各杆的内力。
(b)题6-3图6-4 试求图示组合结构中各链杆的轴力并作受弯杆件的M 、Q 图。
(a)题6-4图6-5 用适宜方法求桁架中指定杆内力。
(c)(b)(a)题6-6图习题88-1 试作图示悬臂梁的反力V B 、M B 及内力Q C 、M C 的影响线。

第四章 平面机构的力分析题4-7机械效益Δ是衡量机构力放大程度的一个重要指标,其定义为在不考虑摩擦的条件下机构的输出力(力矩)与输入力(力矩)之比值,即Δ=d r d r F F M M //=。
试求图示各机构在图示位置时的机械效益。
图a 所示为一铆钉机,图b 为一小型压力机,图c 为一剪刀。
计算所需各尺寸从图中量取。
(a ) (b) (c)解:(a)作铆钉机的机构运动简图及受力 见下图(a )由构件3的力平衡条件有:02343=++R R rF F F由构件1的力平衡条件有:04121=++d R R按上面两式作力的多边形见图(b )得θcot ==∆d r F F(b )作压力机的机构运动简图及受力图见(c )由滑块5的力平衡条件有:04565=++R R F F G由构件2的力平衡条件有:0123242=++R R R 其中 5442R R =按上面两式作力的多边形见图(d ),得tF G =∆(c) 对A 点取矩时有 b F a F d r ⋅=⋅ab =∆其中a 、b 为F r 、F d 两力距离A 点的力臂。
tF G =∆(d)(a)(b)drR41F R43F dG题4-8在图示的曲柄滑块机构中,设已知l AB=0.1m,l BC=0.33m,n1=1500r/min(为常数),活塞及其附件的重量G3=21N,连杆质量G2=25N,J S2=0.0425kg·m2,连杆质心S2至曲柄销B的距离l BS2=l BC/3。
试确定在图示位置时活塞的惯性力以及连杆的总惯性力。
解:1) 选定比例尺, mmml005.0=μ绘制机构运动简图。
(图(a) )2)运动分析:以比例尺vμ作速度多边形,如图(b)以比例尺aμ作加速度多边形如图4-1 (c)244.23smcpaaC=''=μ2222100smspaaS=''=μ22215150sBCcnlalaBCtBC=''==μμα3) 确定惯性力活塞3:)(37673333NagGamFCSI=-=-=方向与cp''相反。

诚信保证本人知晓我校考场规则和违纪处分条例的有关规定,保证遵守考场规则,诚实做人。
本人签字: 编号:西北工业大学考试试题(卷)2004 - 2005学年第 1 学期开课学院 航空学院 课程 飞行器结构力学基础 学时 50考试日期 2004-12-8 考试时间 2 小时 考试形式(闭开)(B A)卷考生班级学 号姓 名成绩第一题(40分) 本题有10个小题,每小题4分,答案及简要运算写在试题空白处。
1.1 试分析图1-1所示平面桁架的几何不变性,并计算其静不定次数f 。
解:几何特性为:=f1.2 绘出图1-2所示平面桁架的传力路线,在图上将传力杆件描粗。
1.3 判断图1-3所示平面刚架的静不定次数f 。
解:=f共4页 第1页西北工业大学命题专用纸图1-1图1-21.4 判断图1-4所示平面桁架的几何不变性,并计算其静不定次数f 。
解:几何特性为: =f1.4 列出1-5所示平面刚架的弯矩方程)(θM M =,给出A 、B 、C 三点的弯矩值。
解:=)(θM=A M=B M=C M1.6 棱柱壳体剖面为正方形,受扭矩T M 作用,如图1-6所示。
绘出剖面剪流分布图,标出剪流大小和方向。
解:1.7 不必具体计算,绘出图1-7所示垂直壁受y Q 作用时的剪流分布图形及方向。
集中面积f 和等厚度t 的壁板都能承受正应力。
图1-412 34567M Ta a1234图1-6f f yxaa /2o图1-5共4页第2页西北工业大学命题专用纸1.8 求图1-8所示平面桁架中杆3-8的轴力38N 。
解:1.9 求图1-9所示二缘条剖面棱柱壳体的弯心位置CR x ,假设壁不受正应力。
解:1.10 说明力法中柔度系数ii δ、)(j i ij ≠δ和位移法中刚度系数ii k 、)(j i k ij ≠的物理意义。
解:ii δ—ij δ—ii k —ij k —图1-8共4页第3页西北工业大学命题专用纸第二题(20分) 矩形平面框,在A、B两截面处受集中力偶M o,如图3所示。

结构力学 第四章习题 参考答案2005级4-1 图示抛物线拱的轴线方程24(fy x l l=−)x ,试求截面K 的内力。
解:(1) 求支座反力801155 kN 16AV AV F F ×=== 0805(5580)0.351500.93625 kN 16BV BV F F ×==−×+×== 0Mc 55880350 kN 4H F f ×−×===(2) 把及代入拱轴方程有:16m l =4m f =(16)16xy =−x (1)由此可得:(8)tan '8x y θ−==(2) 把截面K 的横坐标 ,代入(1),(2)两式可求得: 5m x ==>, 3.44m y =tan 0.375θ= 由此可得:20.56θ= 则有sin 0.351θ=,cos 0.936θ=最后得出截面k 处的内力为: (上标L 表示截面K 在作用力左边,R 则表示截面在作用力右边)055550 3.44103 kN m K H M M F y =−=×−×=i0cos sin 550.936500.35133.93 kN L sK s H F F F θθ=−=×−×= (5580)0.936500.35140.95 kN R sK F =−×−×==40.95 KN 0sin cos 550.351500.93666.1 kN L NK s H F F F θθ=+=×+×= (5580)0.351500.93638.03 kN R NK F =−×+×=4-2 试求拉杆的半圆三铰拱截面K 的内力。
解:(1)以水平方向为X 轴,竖直方向为Y 轴取直角坐标系,可得K 点的坐标为:2m6mK K x y =⎧⎪⎨==⎪⎩ (2)三铰拱整体分别对A ,B 两点取矩,由平衡方程可解得支座反力:0 20210500 20210500 2100A By B Ay x Ax M F M F F F ⎧=×−××⎪⎪=×+××⎨⎪=−×=⎪⎩∑∑∑=== => 5 kN ()20 kN () 5 kN ()Ay Ax By F F F =−⎧⎪=−⎨⎪=⎩向下向上向左(3)把拱的右半部分隔离,对中间铰取矩,列平衡方程可求得横拉杆轴力为:CN 0 105100MF =×−×∑=>N 5 kN F =(4)去如图所示的α角,则有:=>cos 0.6sin 0.8θθ=⎧⎨=⎩于是可得出K 截面的内力,其中:22(6)206525644 kN m 2K M ×=−+×−×−×=isK F (20265)sin 5cos 0.6 kN θθ=−×−×−×=− NK F (20265)cos 5sin 5.8 kN θθ=−−×−×−×=−13K M F r Fr ==(内侧受拉) K 截面作用有力,剪力有突变 且有01sin3032LSK 2F F F F =−=−×=− (2) 22R SK F FF F =−=(3)011sin30(326NKF F F F ==×=拉力)(4)4-4 试求图示三铰拱在均布荷载作用下的合理拱轴线方程。
![[西北工业大学]结构力学(202104)](https://uimg.taocdn.com/faf63c9e5acfa1c7ab00cc9f.webp)
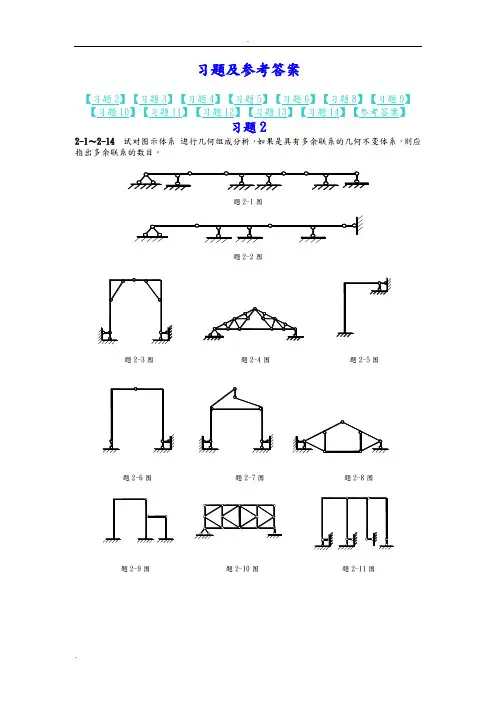
习题及参考答案【习题2】【习题3】【习题4】【习题5】【习题6】【习题8】【习题9】【习题10】「习题11】【习题12】【习题13】【习题14】【参考答衆】习题22-1〜2-14试对图示体系进行儿何组成分析,如果是只有多余联系的儿何不变体系,则应指出多余联系的数目。
d5∑° X 厂^τ"βH题2-2图ΓΛ题2-3图题2-5图题2-6图题2-1图H 2-9 图题2-10图题2-11图题2-12图题2-13图习题3试作图示多跨挣定梁的M及Q图。
(a) (b)题3-1图3-2试不计算反力而绘出梁的M图。
题3-2图习题44-1作图示刚架的M、Q、N图。
40fcN 40kN20kNm4-2作图示刚架的M图。
2OkN m SkN mSkXm 40fcN题4-1图4-3作图示三狡刚架的M图。
4-4作图示刚架的M图。
AEmJnIAr lD1题4-2图4-5己知结构的M图•试绘出荷载。
题4-4图3IOkNnlJ^1.5mC(a)题4-3日6erIB9 9题5-1图5-2带拉杆拱,拱轴线方程y= il(l-χ)χ,求截面K 的弯矩。
题5-2图5-3试求图示带拉杆的半圆三狡拱截面K 的内力・4-6检査F 列刚架的M 图,并予以改正。
题4-5图ω∙I ∣ULL∏ ∏ ⅛)题4-6图习题5图示抛物纟戈三铁拱轴线方程y = ff(l-x)x ,试求D 截面的内力。
IkNm15m [ 5m [ ICm 1=3OmC题5-3图习题6 6-1判定图示桁架中的零杆。
题6-1图6-2用结点法计算图示桁架中各杆内力。
(a) FGH月Λ4x4m=16m题6-2图6-3用截面法计算图示桁架中指定各杆的内力。
40kN题6-3图6-4试求图示组介结构中齐链杆的轴力并作受弯杆件的Q图。
2m ] 2m ]lm]lπ⅝] 2m [题6-4图6-5用适宜方法求桁架中指定杆内力。
题6-6图习题88-1试作图示悬臂梁的反力V B 、MB 及内力Q C 、MC 的影响线。
第四章 力法4-1 利用对称与反对称条件,简化图4-15所示各平面刚架结构,要求画出简化图及其位移边界条件。
P P(a)(a)解:对称结构,在对称载荷作用下,在对称轴上反对称内力为零。
由静力平衡条件∑=0X可得23P N =再由两个静力平衡条件,剩余4个未知力,为二次静不定。
本题中通过对称性条件的使用,将6次静不定的问题转化为2次静不定。
1PP(b)(b)解:对称结构,在反对称载荷作用下,在对称轴上对称的内力为零。
受力分析如图所示有2根对称轴,结合平衡方程,剩下三个未知数,为3次静不定。
本题中通过对称性条件的使用,将6次静不定问题转化为3次静不定。
(c)(c)解:对称结构,在对称载荷作用下,在对称轴上反对称内力为零。
有一根对称轴,减少了两个静不定度本题中通过对称性条件的使用,将3次静不定问题转化为1次静不定。
4-2图4-16所示桁架各杆的EA均相同,求桁架各杆的内力。
(a)(a)解:1、分析结构静不定次数。
结构有4个结点8个自由度,6根杆6个约束,3个外部约束。
因此结构静不定次数为1,f=1。
2、取基本状态。
切开2-4杆,取<P>,<1>状态,各杆内力如图。
1234P-P √2P<P>1234P<1>11√22√22√22√22计算影响系数∑=∆EAl N N i p P 11()2422222+=⎪⎪⎭⎫ ⎝⎛⨯+⨯=EA Pa P P EA a ∑=EAl N i1211δ()22222142222+=⎪⎪⎭⎫ ⎝⎛⨯⨯+⨯⨯=EA a EA a 列正则方程:()()02242221=+++P X解之()P X 42321-=3、由11N X N N P +=,得()P X N 423220112-=⎪⎪⎭⎫ ⎝⎛-⋅+= ()P X P N 42212113+=⋅+=()P X N 423220114-=⎪⎪⎭⎫ ⎝⎛-⋅+=()P X N 423220123-=⎪⎪⎭⎫ ⎝⎛-⋅+=()P X N 423210124-=⋅+=()P X P N 42122134+-=⎪⎪⎭⎫ ⎝⎛-⋅+-=4、校核。
西北工业大学结构力学试卷及其答案一、单项选择题(每小题2分,共20分)1. 下图中的哪一个不是二元体(或二杆节点)()A. B. C. D.2. 图1所示体系,铰K相当的约束个数为()图1 图 2 图3A. 4B. 5C. 6D. 73. 不考虑轴向变形,图2所示结构用先处理法建立的结构刚度矩阵阶数是 ( )A. 3×3B. 4×4C. 5×5D. 6×64. 静定结构的支座反力或内力,可以通过解除相应的约束并使其产生虚位移,利用刚体虚功方程即可求解,虚功方程相当于()A. 几何方程B. 物理方程C. 平衡方程D. 位移方程5. 图3所示结构,用力法求解时最少未知个数为()A. 2B. 3C. 4D. 56. 图示结构中,不能直接用力矩分配法计算的结构是( )A. B. C. D.7. 根据影响线,使跨中截面K产生最大弯矩的均布活荷载最不利分布是( )A. B.C. D.8. 图示三单跨梁的自振频率分别为ωa,ωb,ωc,它们之间的关系是( )(a) (b) (c)A. cbaωωω>> B.bcaωωω>> C.bacωωω>> D.cabωωω>>9. 静定结构在支座移动时,会产生:()A. 内力B. 应力C. 刚体位移D. 变形10. 力法方程是沿基本未知量方向的:()A.力的平衡方程B.位移为零方程C.位移协调方程 D.力的平衡及位移为零方程。
二、填空题(每空2分,共20分)1. 具有基本部分和附属部分的结构,进行受力分析的次序是:先计算____部分,后计算____部分。
2. 图4所示桁架中杆a、b的轴力分别为F Na=____,F Nb=____。
图4 图5 图63. 图5所示静定梁在移动荷载作用下,截面C的弯矩影响线方程为MC=___________(0≤x≤2m);MC=_____(2m≤x≤6m)。
静定结构的位移计算习题4—1 (a)用单位荷载法求图示结构B 点的水平位移解:1. 设置虚拟状态选取坐标如图。
2. M P 图和 如图示3. 虚拟状态中各杆弯矩方程为实际状态中各杆弯矩方程为M P =F P x4. 代入公式(4—6)得 △BH =l 实际状态 1虚拟状态5F P l 15l 1 M P 图图M 图M xM =141012118111EI F EI x F x EI x F x EI dx M M P l l P l P P =⨯⨯+⨯⨯=∑⎰⎰⎰(←)4—1 (b)单位荷载法求图示刚架B 点的水平位移 解:1. 设置虚拟状态选取坐标如图。
2. M P 图和 如图示3. 虚拟状态中各杆弯矩方程为 BD: DC: CA: 实际状态中各杆弯矩方程为 BD: M P =0 DC: M P =40x CA: M P =160+5x 24. 代入公式(4—6)得图M x M =3=M xM-=3△BH =4—2试求图示桁架结点B 的竖向位移,已知桁架各杆的EA =21×104KN 。
1M P 图图M 3KN •m340KN •m3KN •m3KN •m5160)3(40306012401301+⨯-+⨯+*=∑⎰⎰⎰⎰EI x x x EI x EI x EI dxM M P解:虚拟状态如图示。
实际状态和虚拟状态所产生的杆件内力均列在表中,4—1根据式4—7可得结点B 的竖向位移为表4—1中)(768.010215.16124↓=⨯•=∆cm KNm KNBV实际状态虚拟状态4—3 (a)、(b)试用图乘法求图示结构B处的转角和C处的竖向位移。
EI=常数。
(a )解:M P 图、单位力偶下作用于BM=ql 2M P图ql 2/81M=1点的1M 图、单位力下作用于C 点的2M 图EIql ql l ql l EI B 3)21223232221(1222=⨯⨯⨯-⨯⨯⨯=ϕ( )(b )解:M P图、单位力偶下作用于B 点的1M 图、单位力作用于C 点的2M 图)2183232421(122⨯⨯⨯-⨯⨯⨯=ql l l ql EI B ϕ=ql 3/24EI( ))23242212832232421(1222ql ql l ql ql l ql l ql EI cv ⨯⨯⨯⨯+⨯⨯⨯-⨯⨯⨯⨯=∆= ql 4/24EI(↓))(24)2852232322213221(14222↑-=⨯⨯⨯⨯⨯+⨯⨯⨯-⨯⨯⨯-=∆EI qll ql l ql l l ql l l EI CV((b )ql/2ll单位力偶作用于B点的1M图、单位力作用于C点时的2M图EIlFlFllFlEIPPPB1223121122322121(12=⨯⨯⨯⨯+⨯⨯⨯⨯⨯-=ϕ( ))(12231212232221(12↓=⨯⨯⨯⨯+⨯⨯⨯⨯⨯-=∆EIlFlFlllFllEIPPPcv4—4(a)试求图示结构C点的竖向位移。
结构力学课后习题答案4结构力学课后习题答案4结构力学是工程学中非常重要的一门学科,它研究物体在受到外力作用下的变形和破坏行为。
通过学习结构力学,我们可以更好地理解和分析各种工程结构的力学性能,为工程设计和施工提供有力的支持。
下面是结构力学课后习题的答案,希望对大家的学习有所帮助。
1. 问题描述:一个悬臂梁的长度为L,横截面形状为矩形,宽度为b,高度为h。
在悬臂梁的自重作用下,梁的挠度为δ。
求悬臂梁在距离支点x处的弯矩M和剪力V。
解答:根据悬臂梁的受力分析,距离支点x处的弯矩M可以通过以下公式计算:M = -wLx + 1/2wL^2其中,w为单位长度的梁的自重。
剪力V可以通过以下公式计算:V = wL - wx2. 问题描述:一个梁的长度为L,横截面形状为矩形,宽度为b,高度为h。
在梁的两端分别施加一个向下的集中力P。
求梁在距离支点x处的弯矩M和剪力V。
解答:根据梁的受力分析,距离支点x处的弯矩M可以通过以下公式计算:M = -Px + P(L-x)剪力V可以通过以下公式计算:V = P3. 问题描述:一个梁的长度为L,横截面形状为矩形,宽度为b,高度为h。
在梁的两端分别施加一个向下的集中力P。
梁的弹性模量为E,截面惯性矩为I。
求梁在距离支点x处的挠度δ。
解答:根据梁的受力分析,梁在距离支点x处的挠度δ可以通过以下公式计算:δ = (Px(L^2-x^2))/(6EI)4. 问题描述:一个梁的长度为L,横截面形状为矩形,宽度为b,高度为h。
在梁的两端分别施加一个向下的集中力P。
梁的弹性模量为E,截面惯性矩为I。
求梁在距离支点x处的剪力V。
解答:根据梁的受力分析,梁在距离支点x处的剪力V可以通过以下公式计算:V = P(L-x)/L5. 问题描述:一个梁的长度为L,横截面形状为矩形,宽度为b,高度为h。
在梁的两端分别施加一个向下的集中力P。
梁的弹性模量为E,截面惯性矩为I。
求梁在距离支点x处的弯矩M。
第三章 静定结构的位移计算一、判断题:1、虚位移原理等价于变形谐调条件,可用于求体系的位移。
2、按虚力原理所建立的虚功方程等价于几何方程。
3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下,静定结构不产生内力,但会有位移且位移只与杆件相对刚度有关。
4、求图示梁铰C 左侧截面的转角时,其虚拟状态应取:A.;; B.D.C.M =15、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。
6、已知M p 、M k 图,用图乘法求位移的结果为:()/()ωω1122y y EI +。
M k M p7、图a 、b 两种状态中,粱的转角ϕ与竖向位移δ间的关系为:δ=ϕ 。
8、图示桁架各杆E A 相同,结点A 和结点B 的竖向位移均为零。
9、图示桁架各杆EA =常数,由于荷载P 是反对称性质的,故结点B 的竖向位移等于零。
二、计算题:10、求图示结构铰A 两侧截面的相对转角ϕA ,EI = 常数。
q l l l /211、求图示静定梁D 端的竖向位移∆DV 。
EI = 常数,a = 2m 。
a a a 10kN/m12、求图示结构E 点的竖向位移。
EI = 常数。
l l l /3/3q13、图示结构,EI=常数,M =⋅90kN m , P = 30kN 。
求D 点的竖向位移。
P 3m 3m 3m14、求图示刚架B 端的竖向位移。
ql15、求图示刚架结点C 的转角和水平位移,EI = 常数。
16、求图示刚架中D点的竖向位移。
EI=常数。
l/217、求图示刚架横梁中D点的竖向位移。
EI =常数。
18、求图示刚架中D 点的竖向位移。
E I = 常数 。
ql l/219、求图示结构A、B两截面的相对转角,EI =常数。
l/23l/320、求图示结构A 、B 两点的相对水平位移,E I = 常数。
l l21、求图示结构B 点的竖向位移,EI =常数。
l l22、图示结构充满水后,求A 、B 两点的相对水平位移。
第四章 力法4-1 利用对称与反对称条件,简化图4-15所示各平面刚架结构,要求画出简化图及其位移边界条件。
P P(a)(a)解:对称结构,在对称载荷作用下,在对称轴上反对称内力为零。
由静力平衡条件∑=0X可得23P N =再由两个静力平衡条件,剩余4个未知力,为二次静不定。
本题中通过对称性条件的使用,将6次静不定的问题转化为2次静不定。
1PP(b)(b)解:对称结构,在反对称载荷作用下,在对称轴上对称的内力为零。
受力分析如图所示有2根对称轴,结合平衡方程,剩下三个未知数,为3次静不定。
本题中通过对称性条件的使用,将6次静不定问题转化为3次静不定。
(c)(c)解:对称结构,在对称载荷作用下,在对称轴上反对称内力为零。
有一根对称轴,减少了两个静不定度本题中通过对称性条件的使用,将3次静不定问题转化为1次静不定。
4-2图4-16所示桁架各杆的EA均相同,求桁架各杆的内力。
(a)(a)解:1、分析结构静不定次数。
结构有4个结点8个自由度,6根杆6个约束,3个外部约束。
因此结构静不定次数为1,f=1。
2、取基本状态。
切开2-4杆,取<P>,<1>状态,各杆内力如图。
1234P-P √2P<P>1234P<1>11√22√22√22√22计算影响系数∑=∆EAl N N i p P 11()2422222+=⎪⎪⎭⎫ ⎝⎛⨯+⨯=EA Pa P P EA a ∑=EAl N i1211δ()22222142222+=⎪⎪⎭⎫ ⎝⎛⨯⨯+⨯⨯=EA a EA a 列正则方程:()()02242221=+++P X解之()P X 42321-=3、由11N X N N P +=,得()P X N 423220112-=⎪⎪⎭⎫ ⎝⎛-⋅+= ()P X P N 42212113+=⋅+=()P X N 423220114-=⎪⎪⎭⎫ ⎝⎛-⋅+=()P X N 423220123-=⎪⎪⎭⎫ ⎝⎛-⋅+=()P X N 423210124-=⋅+=()P X P N 42122134+-=⎪⎪⎭⎫ ⎝⎛-⋅+-=4、校核。
结点2:0=∑X ∑=0Y 结点3:0=∑X ∑=0Y(b)(b)解: 1、分析结构静不定次数。
结构有4个结点8个自由度,5根杆5个约束,4个外部约束。
因此结构静不定次数为1,f=1。
2、取基本状态。
切开2-4杆,取<P>,<1>状态,各杆内力如图。
2√2P 22<P>123411>1<√22√22√22计算影响系数∑=∆EAl N N ip P 11()221222222+=⎪⎪⎭⎫ ⎝⎛⨯+⨯=EA Pa P P EA a ∑=EAl N i1211δ()243222132222+=⎪⎪⎭⎫ ⎝⎛⨯⨯+⨯⨯=EA aEA a 列正则方程:()()0212431=+++P X解之()P X 23521+-= 3、由11N X N N P +=,得()P X P N 2312142222112+=⎪⎪⎭⎫ ⎝⎛-⋅+=()PX P N 232181113-=⋅+=P X P N 182912222123--=⎪⎪⎭⎫ ⎝⎛-⋅+-=P X N 232510124+-=⋅+= P X P N 182912222134-=⎪⎪⎭⎫ ⎝⎛-⋅+-=4、校核。
结点2:0=∑X ∑=0Y 结点3:0=∑X ∑=0Y(c)(c)解:1、分析结构静不定次数。
结构有4个结点8个自由度,3根杆3个约束,6个外部约束。
因此结构静不定次数为1,f=1。
2、取基本状态。
切开1-2杆,取<P>,<1>状态,各杆内力如图。
234P-2P √3P<P>2341-2√3<1>计算影响系数()()()3243232231+-=⎥⎦⎤⎢⎣⎡⨯⨯-+-⨯=∆EA PaP P EA a P()32621132332211+=⎪⎭⎫ ⎝⎛⨯⨯+⨯⨯+⨯=EAaEA a δ 列正则方程:()()03243261=+-+X 解之 ()P X 6331+=3、由11N X N N P +=,得 ()P X N 63310112+=⋅+=()P X P N 23332123-=⋅+-= ()()P X P N 333223124-=-⋅+= 4、校核。
结点2:0=∑X ∑=0Y(d)(d)解:1、分析结构静不定次数。
结构有4个结点8个自由度,5根杆5个约束,4个外部约束。
因此结构静不定次数为1,f=1。
2、取基本状态。
切开1-2杆,取<P>,<1>状态,各杆内力如图。
计算影响系数EAPcP EA c P 3223131=⎪⎪⎭⎫ ⎝⎛⨯⨯=∆ ()332333312313111+=⎪⎪⎭⎫ ⎝⎛⨯⨯+⨯⨯=EAcEA c δ 列正则方程:()023321=++P X 解之()P X 233641-=3、由11N X N N P +=,得()P X N 2336410112-=⋅+=()P X P N 23396313113-=⎪⎪⎭⎫ ⎝⎛-⋅+-= ()P N N 233961314-==()P X N 2336410123-=⋅+=()P N N 233642324-==4、校核。
结点2:0=∑X ∑=0Y 结点3:0=∑X ∑=0Y4-3 图4-17所示平面刚架的EJ 为常数,求刚架的弯矩并绘制弯矩图。
(a)(a)解: 1、由于结构对称,取其一半为计算模型。
2、分析计算模型静不定次数。
计算模型由1根杆3个自由度,4个外部约束。
因此计算模型的静不定次数为1,f=1。
3、取基本状态。
切开1-2杆,取<P>,<1>状态,各杆内力如图。
R 12P12Pα<P>12α<1>M=1<P>状态:()1cos sin 2-+=ααPRM P <1>状态:αcos 1=M 计算影响系数()()EJ PR d PREJP82cos 1cos sin 21201-=⋅-+=∆⎰πααααπEJd EJ4cos 120211πααδπ==⎰列正则方程: ()02211=-+PR X ππ 解之()ππ221PR X -=4、由11N X N N P +=,得 ()⎪⎭⎫ ⎝⎛-+=⋅+-+=1cos 2sin 2cos 1cos sin 21απααααPR X PR M 5、校核。
(b)(b) 解:1、分析结构静不定次数。
结构有1根杆3个自由度,4个外部约束。
因此结构静不定次数为1,f=1。
2、取基本状态。
去掉可动铰支座,取<P>,<1>状态,各杆内力如图。
234<P>αP234<1>α<P>状态:23段:αsin 23PR M P = 34段:PR M P =34<1>状态:23段:023=M 34段:x M =23 计算影响系数312121PR PR R R P =⨯⨯=∆ 3211313221R R R =⨯=δ列正则方程:0321=+P X 解之P X 231-= 3、由11N X N N P +=,得23段:αsin PR M =34段:PR x X PR M =⋅+=1P 23-x 4、校核。
4-4 求图4-16(a)、(b)、(c)桁架结构点2的水平位移;图(d)桁架结构点2的垂直位移。
(a)解:由4-2(a)的解答,在基本系统的2点加水平单位力,内力如图。
1234101因此2点的水平位移, ∑=∆EANl N P x 2()()Pa EAP EA a 4231423-=⨯-⨯=(b)解:由4-2(b)的解答,在基本系统的2点加水平单位力,内力如图。
123411因此2点的水平位移, ∑=∆EA Nl N P x 2()()Pa EAP EA a 2322181232218-=⨯-⨯=(c)解:由4-2(c)的解答,在基本系统的2点加水平单位力,内力如图。
2341-2√3因此2点的水平位移∑=∆EA Nl N P x 2()()()Pa EAP EA a P EAa333334225332=⨯-⨯+-⨯-⨯=(d)解:由4-2(d)的解答,在基本系统的2点加垂直单位力,内力如图。
2341-1-1100因此2点的垂直位移, ∑=∆EANlN P y 2()()()Pc EAP EA c 693836123364332-=-⨯-⨯⨯=4-5 求图4-18所示静不定刚架结构在常剪流q 作用下B 截面的转角。
图 4-18解: 1、分析结构静不定次数。
结构有1根杆3个自由度,4个外部约束。
因此结构静不定次数为1,f=1。
2、取基本状态。
去掉可动铰支座,取<P>,<1>状态,各杆内力如图(弯矩顺时针为正)。
α<P>PB<1>1B<P>状态:()()αααααsin cos 120--=-⋅-=⎰qR R qRd M P<1>状态:αsin 1R M =计算影响系数()()()4202144sin sin 1qR EJd R R qR EJpπααααπ-=⋅--=∆⎰()3202114sin 1R EJRd R EJπααδπ==⎰列正则方程;()041=-+qR X ππ解之qR X ππ41-=3、由11N X N N P +=,得()()⎪⎭⎫⎝⎛-=⋅+--=ααπαααsin 4sin sin 212qR R X qR M 4、在基本系统的1点加上单位弯矩,顺时针为正,内力如图:M=1B1'=P M 因此B 截面的转角,EJ qR Rd qR EJ B 32202841sin 41⎪⎪⎭⎫ ⎝⎛-=⋅⋅⎪⎭⎫⎝⎛-=⎰ππαααπϕπ。