西北工业大学航空学院结构力学答案 第四章 力法

西工大飞行器结构力学课后答案第一题根据飞机结构力学的基本原理，飞机的结构力学可以被分解为静力学和动力学两个部分。

静力学是研究在静止或恒定速度下的力学行为，包括计算飞机各个部件的受力和应变情况。

而动力学则是研究在变化速度和加速度下的力学行为，包括计算飞机受到的各种动力荷载和振动情况。

第二题飞机的结构力学分析中，常用的方法包括有限元分析、静力学分析和动力学分析。

有限元分析是一种基于数值计算的方法，可以建立飞机结构的数学模型，并以此模型进行力学分析。

静力学分析是通过平衡方程来计算飞机结构的受力和应变情况，包括应力分析和变形分析。

动力学分析是通过力学方程来计算飞机在动态载荷下的振动响应和疲劳寿命。

第三题飞机的结构力学分析对于设计和制造过程中的决策具有重要意义。

在设计阶段，结构力学分析可以帮助工程师评估不同设计方案的有效性和可行性。

通过分析飞机的受力和应变情况，可以优化设计，并确保飞机在正常工作范围内具有足够的强度和刚度。

在制造阶段，结构力学分析可以帮助工程师确定合适的材料和加工工艺，以确保飞机结构的可靠性和安全性。

通过分析飞机的受力和应变情况，可以预测飞机在使用寿命内的疲劳寿命，并采取相应的措施延长飞机的使用寿命。

此外，结构力学分析还可以应用于飞机维修和事故调查过程中。

通过分析事故飞机的受力和应变情况，可以确定事故原因，并提出相应的维修和改进建议，以减少事故的发生对飞机结构的影响。

第四题对于飞行器结构力学的研究，需要掌握一些基本理论和方法。

首先是静力学的基本原理，包括力的平衡方程、应力和应变的定义和计算方法。

其次是动力学的基本原理，包括力的运动方程、振动的模型和计算方法。

此外，还需要了解一些基本的力学性能指标，如强度和刚度。

在进行结构力学分析时，需要掌握一些基本的计算方法。

常见的方法包括有限元法、解析法和试验法。

有限元法是一种基于数值计算的方法，可以建立飞机结构的数学模型，并以此模型进行力学分析。

解析法则是通过解析计算的方法进行力学分析，主要针对简单和规则的结构。

结构力学 第四章习题 参考答案2005级4－1 图示抛物线拱的轴线方程24(fy x l l=−)x ，试求截面K 的内力。

解：（1） 求支座反力801155 kN 16AV AV F F ×=== 0805(5580)0.351500.93625 kN 16BV BV F F ×==−×+×== 0Mc 55880350 kN 4H F f ×−×===（2） 把及代入拱轴方程有:16m l =4m f =(16)16xy =−x （1）由此可得:(8)tan '8x y θ−==（2） 把截面K 的横坐标 ,代入（1），（2）两式可求得: 5m x ==＞, 3.44m y =tan 0.375θ= 由此可得:20.56θ= 则有sin 0.351θ=,cos 0.936θ=最后得出截面k 处的内力为: (上标L 表示截面K 在作用力左边，R 则表示截面在作用力右边)055550 3.44103 kN m K H M M F y =−=×−×=i0cos sin 550.936500.35133.93 kN L sK s H F F F θθ=−=×−×= (5580)0.936500.35140.95 kN R sK F =−×−×==40.95 KN 0sin cos 550.351500.93666.1 kN L NK s H F F F θθ=+=×+×= (5580)0.351500.93638.03 kN R NK F =−×+×=4－2 试求拉杆的半圆三铰拱截面K 的内力。

解：（1）以水平方向为X 轴,竖直方向为Y 轴取直角坐标系，可得K 点的坐标为：2m6mK K x y =⎧⎪⎨==⎪⎩ （2）三铰拱整体分别对A ，B 两点取矩，由平衡方程可解得支座反力：0 20210500 20210500 2100A By B Ay x Ax M F M F F F ⎧=×−××⎪⎪=×+××⎨⎪=−×=⎪⎩∑∑∑=== =＞ 5 kN ()20 kN () 5 kN ()Ay Ax By F F F =−⎧⎪=−⎨⎪=⎩向下向上向左（3）把拱的右半部分隔离，对中间铰取矩，列平衡方程可求得横拉杆轴力为：CN 0 105100MF =×−×∑=＞N 5 kN F =（4）去如图所示的α角，则有：=＞cos 0.6sin 0.8θθ=⎧⎨=⎩于是可得出K 截面的内力，其中：22(6)206525644 kN m 2K M ×=−+×−×−×=isK F (20265)sin 5cos 0.6 kN θθ=−×−×−×=− NK F (20265)cos 5sin 5.8 kN θθ=−−×−×−×=−13K M F r Fr ==（内侧受拉） K 截面作用有力，剪力有突变 且有01sin3032LSK 2F F F F =−=−×=− （2） 22R SK F FF F =−=（3）011sin30(326NKF F F F ==×=拉力）（4）4-4 试求图示三铰拱在均布荷载作用下的合理拱轴线方程。

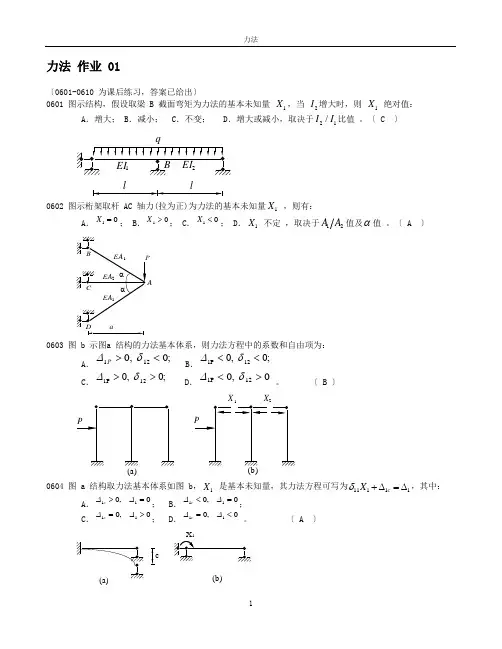
力法 作业 01〔0601-0610 为课后练习，答案已给出〕0601 图示结构，假设取梁 B 截面弯矩为力法的基本未知量 1X ，当 2I 增大时，则 1X 绝对值：A ．增大；B ．减小；C ．不变；D ．增大或减小，取决于21/I I 比值 。

〔 C 〕q0602 图示桁架取杆 AC 轴力(拉为正)为力法的基本未知量1X ，则有：A ．X 10=；B ．X 10>；C ．X 10<；D ．1X 不定 ，取决于12A A 值及α值 。

〔 A 〕aD0603 图 b 示图a 结构的力法基本体系，则力法方程中的系数和自由项为：A ．∆11200P ><,; δB ．∆11200P <<,;δC ．∆11200P >>,;δ D ．∆11200P <>,δ 。

〔 B 〕X X0604 图 a 结构取力法基本体系如图 b ，1X 是基本未知量，其力法方程可写为11111c X δ+∆=∆，其中： A ．∆∆1100c >=,； B ．∆∆1100c<=,；C ．∆∆1100c =>,； D ．∆∆1100c =<, 。

〔 A 〕(a)(b)X 10605 图 a 结构的最后弯矩图为 ：A ．图 b ；B ．图 c ；C ．图 d ；D ．都不 对 。

〔 A 〕l 3M /4M /4(a)(b)M /43M /4M /8M /43M /4M /2(c)(d)0606 图示结构 f (柔 度) 从小到大时，固定端弯矩 m 为：A ．从小到大；B ．从大到小；C ．不变化;D ． m 反向 。

〔 B 〕0607 图示对称结构，其半结构计算简图为图：B.原 图〔 A 〕0608图示结构( f 为柔度)：A ．M MA C >;B ．M M AC =; C ．M M A C <;D ．M M A C =- 。

结构力学（202104）
一、单选题
1.下列哪种支座提供1个约束反力。

()
A.
B.
C.
D.
答案：A
2.一个平面刚片的自由度等于()。

A.1
B.2
C.3
D.4
答案：C
3.三刚片用三个单铰连接，当三个单铰共线时体系为()。

A.几何可变体系
B.几何不变体系
C.瞬变体系
D.不能确定
答案：C
4.图示超静定结构，如果用力法求解，则基本未知量个数为()。

A.1个
B.2个
C.3个
D.5个
答案：D
5.进行体系计算自由度的计算时，连接3个刚片的复铰相当于()个单铰。

A.1
B.2.
C.3
D.4
答案：B
6.静定结构在支座时，会产生()。

A.内力
B.应力
C.刚性位移
D.变形
答案：C
7.图乘法求位移的必要条件之一是()。

A.单位荷载下的弯矩图为一直线
B.结构可分为截面直杆段
C.所有杆件EI为常数且相同。

诚信保证本人知晓我校考场规则和违纪处分条例的有关规定，保证遵守考场规则，诚实做人。

本人签字： 编号：西北工业大学考试试题（卷）2004 － 2005学年第 1 学期开课学院 航空学院 课程 飞行器结构力学基础 学时 50考试日期 2004-12-8 考试时间 2 小时 考试形式（闭开）（B A）卷考生班级学 号姓 名成绩第一题(40分) 本题有10个小题，每小题4分，答案及简要运算写在试题空白处。

1.1 试分析图1-1所示平面桁架的几何不变性，并计算其静不定次数f 。

解：几何特性为：=f1.2 绘出图1-2所示平面桁架的传力路线，在图上将传力杆件描粗。

1.3 判断图1-3所示平面刚架的静不定次数f 。

解：=f共4页 第1页西北工业大学命题专用纸图1－1图1－21.4 判断图1-4所示平面桁架的几何不变性，并计算其静不定次数f 。

解：几何特性为： =f1.4 列出1-5所示平面刚架的弯矩方程)(θM M =，给出A 、B 、C 三点的弯矩值。

解：=)(θM=A M=B M=C M1.6 棱柱壳体剖面为正方形，受扭矩T M 作用，如图1-6所示。

绘出剖面剪流分布图，标出剪流大小和方向。

解：1.7 不必具体计算，绘出图1-7所示垂直壁受y Q 作用时的剪流分布图形及方向。

集中面积f 和等厚度t 的壁板都能承受正应力。

图1-412 34567M Ta a1234图1-6f f yxaa /2o图1－5共4页第2页西北工业大学命题专用纸1.8 求图1-8所示平面桁架中杆3-8的轴力38N 。

解：1.9 求图1-9所示二缘条剖面棱柱壳体的弯心位置CR x ，假设壁不受正应力。

解：1.10 说明力法中柔度系数ii δ、)(j i ij ≠δ和位移法中刚度系数ii k 、)(j i k ij ≠的物理意义。

解：ii δ—ij δ—ii k —ij k —图1-8共4页第3页西北工业大学命题专用纸第二题(20分) 矩形平面框，在A、B两截面处受集中力偶M o，如图3所示。

结构力学 第四章习题 参考答案2005级4－1 图示抛物线拱的轴线方程24(fy x l l=−)x ，试求截面K 的内力。

解：（1） 求支座反力801155 kN 16AV AV F F ×=== 0805(5580)0.351500.93625 kN 16BV BV F F ×==−×+×== 0Mc 55880350 kN 4H F f ×−×===（2） 把及代入拱轴方程有:16m l =4m f =(16)16xy =−x （1）由此可得:(8)tan '8x y θ−==（2） 把截面K 的横坐标 ,代入（1），（2）两式可求得: 5m x ==＞, 3.44m y =tan 0.375θ= 由此可得:20.56θ= 则有sin 0.351θ=,cos 0.936θ=最后得出截面k 处的内力为: (上标L 表示截面K 在作用力左边，R 则表示截面在作用力右边)055550 3.44103 kN m K H M M F y =−=×−×=i0cos sin 550.936500.35133.93 kN L sK s H F F F θθ=−=×−×= (5580)0.936500.35140.95 kN R sK F =−×−×==40.95 KN 0sin cos 550.351500.93666.1 kN L NK s H F F F θθ=+=×+×= (5580)0.351500.93638.03 kN R NK F =−×+×=4－2 试求拉杆的半圆三铰拱截面K 的内力。

解：（1）以水平方向为X 轴,竖直方向为Y 轴取直角坐标系，可得K 点的坐标为：2m6mK K x y =⎧⎪⎨==⎪⎩ （2）三铰拱整体分别对A ，B 两点取矩，由平衡方程可解得支座反力：0 20210500 20210500 2100A By B Ay x Ax M F M F F F ⎧=×−××⎪⎪=×+××⎨⎪=−×=⎪⎩∑∑∑=== =＞ 5 kN ()20 kN () 5 kN ()Ay Ax By F F F =−⎧⎪=−⎨⎪=⎩向下向上向左（3）把拱的右半部分隔离，对中间铰取矩，列平衡方程可求得横拉杆轴力为：CN 0 105100MF =×−×∑=＞N 5 kN F =（4）去如图所示的α角，则有：=＞cos 0.6sin 0.8θθ=⎧⎨=⎩于是可得出K 截面的内力，其中：22(6)206525644 kN m 2K M ×=−+×−×−×=isK F (20265)sin 5cos 0.6 kN θθ=−×−×−×=− NK F (20265)cos 5sin 5.8 kN θθ=−−×−×−×=−13K M F r Fr ==（内侧受拉） K 截面作用有力，剪力有突变 且有01sin3032LSK 2F F F F =−=−×=− （2） 22R SK F FF F =−=（3）011sin30(326NKF F F F ==×=拉力）（4）4-4 试求图示三铰拱在均布荷载作用下的合理拱轴线方程。

第1章绪论（无习题）之阳早格格创做第2章仄里体系的机动领会习题解问习题利害推断题(1) 若仄里体系的本质自由度为整，则该体系一定为几许稳定体系.( )(2) 若仄里体系的估计自由度W=0，则该体系一定为无多余拘束的几许稳定体系.( )(3) 若仄里体系的估计自由度W＜0，则该体系为有多余拘束的几许稳定体系.( )(4) 由三个铰二二贯串的三刚刚片组成几许稳定体系且无多余拘束.( )(5) 习题2.1(5) 图所示体系去掉二元体CEF后，结余部分为简收刚刚架，所以本质系为无多余拘束的几许稳定体系.( )习题 2.1(5)图(6) 习题2.1(6)(a)图所示体系去掉二元体ABC后，成为习题2.1(6) (b)图，故本质系是几许可变体系.( )(7) 习题2.1(6)(a)图所示体系去掉二元体EDF后，成为习题2.1(6) (c)图，故本质系是几许可变体系.( )习题 2.1(6)图习题挖空(1) 习题2.2(1)图所示体系为_________体系.习题2.2(1)图(2) 习题2.2(2)图所示体系为__________体系.习题 2-2(2)图(3) 习题2.2(3)图所示4个体系的多余拘束数目分别为_______、________、__________、__________.习题 2.2(3)图(4) 习题 2.2(4)图所示体系的多余拘束个数为___________.习题 2.2(4)图(5) 习题 2.2(5)图所示体系的多余拘束个数为___________.习题 2.2(5)图(6) 习题 2.2(6)图所示体系为_________体系，有_________个多余拘束.习题 2.2(6)图(7) 习题 2.2(7)图所示体系为_________体系，有_________个多余拘束.习题 2.2(7)图对付习题2.3图所示各体系举止几许组成领会.第3章静定梁与静定刚刚架习题解问习题利害推断题(1) 正在使用内力图特性画制某受直杆段的直矩图时，必须先供出该杆段二端的端直矩.（）(2) 区段叠加法仅适用于直矩图的画制，不适用于剪力图的画制.（）(3) 多跨静定梁正在附属部分受横背荷载效率时，必会引起基础部分的内力.（）(4) 习题3.1(4)图所示多跨静定梁中，CDE战EF部分均为附属部分.（）习题3.1(4)图习题挖空(1)习题3.2(1)图所示受荷的多跨静定梁，其定背通联C所传播的直矩M C的大小为______；截里B的直矩大小为______，____侧受推.习题3.2(1)图(2) 习题3.2(2)图所示风载效率下的悬臂刚刚架，其梁端直矩M AB=______kN·m，____侧受推；左柱B截里直矩M B=______kN·m，____侧受推.习题3.2(2)图习题做图所示单跨静定梁的M图战F图.Q(a) (b)(c) (d)(e) (f)习题做图所示单跨静定梁的内力图.(c) 习题做图所示斜梁的内力图.习题做图所示多跨梁的内力图.(a)(a)习题改正图所示刚刚架的直矩图中的过失部分.(a) (b) (c)(d) (e) (f)习题做图所示刚刚架的内力图.(a)(b)第4章静定拱习题解问习题4.1利害推断题(1) 三铰拱的火仄推力不但是与三个铰的位子有关，还与拱轴线的形状有关.（）(2) 所谓合理拱轴线，是指正在任性荷载效率下皆能使拱处于无直矩状态的轴线. （ ）(3) 改变荷载值的大小，三铰拱的合理拱轴线形状也将爆收改变. （ ）习题4.2挖空(1) 习题3.2(3)图所示三铰拱的火仄推力F H 等于.习题3.2(3)图习题4.3供图所示三铰拱收反力战指定截里K 的内力.已知轴线圆程24()f y x l x l =-.第5章 静定仄里桁架习题解问习题5.1 利害推断题(1) 利用结面法供解桁架结构时，可从任性结面启初. （ ） 习题5.2挖空(1)习题3.2(4)图所示桁架中有根整杆.习题3.2(4)图习题5.3 试用结面法供图所示桁架杆件的轴力.(a) (b)习题5.4 推断图所示桁架结构的整杆.(a) (b)(c)习题5.5 用截里法供解图所示桁架指定杆件的轴力.(a)(b)第6章 结构的位移估计习题解问习题6.1 利害推断题(1) 变形骸真功本理仅适用于弹性体系，不适用于非弹性体系.（ ）(2) 真功本理中的力状态战位移状态皆是真设的.（ ）(3) 功的互等定理仅适用于线弹性体系，不适用于非线弹性体系.（ ）(4) 反力互等定理仅适用于超静定结构，不适用于静定结构.（ ）(5) 对付于静定结构，有变形便一定有内力.（ ）(6) 对付于静定结构，有位移便一定有变形.（ ）(7) 习题4.1(7)图所示体系中各杆EA 相共，则二图中C 面的火仄位移相等.（ ）(8) M P 图，M 图如习题4.1(8)图所示，EI =常数.下列图乘截止是精确的：4)832(12l l ql EI ⨯⨯⨯ （ ）(9) M P 图、M (9)图所示，下列图乘截止是精确的：033202201111)(1y A EI y A y A EI ++ （ ）(10) (10)图所示结构的二个仄稳状态中，有一个为温度变更，此时功的互等定理不可坐.（ ）习题 4.1(7)图习题 4.1(8)图 习题4.1(9)图习题 4.1(10)图习题6.2挖空题(1) 习题4.2(1)图所示刚刚架，由于收座B 下重所引起D 面的火仄位移D H =______. (2) 真功本理有二种分歧的应用形式，即_______本理战_______本理.其中，用于供位移的是_______本理.(3) 用单位荷载法估计位移时，假制状态中所加的荷载应是与所供广义位移相映的________.(4) 图乘法的应用条件是：__________且M P 与M 图中起码有一个为直线图形.(5) 已知刚刚架正在荷载效率下的M P 图如习题4.2(5)图所示，直线为二次扔物线，横梁的抗直刚刚度为2EI ，横杆为EI ，则横梁中面K 的横背位移为________.(6) 习题4.2(6)图所示拱中推杆AB 比本安排少度短了，由此引起C 面的横背位移为________；引起收座A 的火仄反力为________.(7) 习题4.2(7)图所示结构，当C 面有F P =1(↓)效率时，D 面横背位移等于(↑)，当E 面有图示荷载效率时，C 面的横背位移为________.(8) 习题 4.2(8)图（a ）所示连绝梁收座B 的反力为)(1611R ↑=B F ，则该连绝梁正在收座B 下重B =1时（如图（b ）所示），D 面的横背位移D δ=________.习题 4.2(1)图 习题 4.2(5)图习题 4.2(6)图 习题 4.2(7)图习题 4.2(8)图习题6.3C V .EI 为常数.1)供C V习题4.3(1)图2)供C V习题4.3(2)图3)供C V习题4.3(3)图4)供A习题4.3（4）图习题6.4 分别用积分法战图乘法供习题4.4(a)图所示刚刚架C 面的火仄位移C H .已知EI =常数.习题6.5 习题4.5(a)图所示桁架各杆截里均为A =2×103m 2，E ×108kN/m 2，F P =30kN ，d =2m.试供C 面的横背位移V C .第7章 力法习题解问习题7.1利害推断题（1）习题5.1(1)图所示结构，当收座A 爆收转化时，D q l l B A C lA B lD C A BC22ql 2ql 281ql 2(b)图M P M 图(c)(a)xx1l各杆均爆收内力.（）习题5.1(1)图习题5.1(2)图（2）习题 5.1(2)图所示结构，当内中侧均降下t1℃时，二杆均只爆收轴力.（）（3）习题 5.1(3)图(a)战(b)所示二结构的内力相共.（）习题5.1(3)图（4）习题 5.1(3)图(a)战(b)所示二结构的变形相共.（）习题7.2 挖空题（1）习题5.2(1) 图(a)所示超静定梁的收座A爆收转角，若选图(b)所示力法基础结构，则力法圆程为_____________，代表的位移条件是______________，其中=_________；若选图(c)所示力法基础结构时，力法圆1c程为____________，代表的位移条件是______________，其中1c=_________.习题5.2(1)图（2）习题5.2(2)图(a)所示超静定结构，当基础体系为图(b)时，力法圆程为____________________，=________；当基础体系为图(c)时，力法圆程为1P____________________，1P=________.习题5.2(2)图（3）习题5.2(3)图(a)所示结构各杆刚刚度相共且为常数，AB杆中面直矩为________，____侧受推；图(b)所示结构M BC=________，____侧受推.习题5.2(3)图（4）连绝梁受荷载效率时，其直矩图如习题5.2(4)图所示，则D面的挠度为________，位移目标为____.习题5.2(4)图习题7.3试决定习题5.3图所示结构的超静定次数.图习题7.4用力法估计习题5.4图所示各超静定梁，并做出直矩图战剪力图.图习题7.5用力法估计习题5.5图所示各超静定刚刚架，并做出内力图.图习题7.6利用对付称性，估计习题5.12图所示各结构的内力，并画直矩图.图习题7.7画出习题5.17图所示各结构直矩图的大概形状.已知各杆EI=常数.图第8章位移法习题解问习题8.1决定用位移法估计图所示结构的基础已知量数目，并画出基础结构.（除证明者中，其余杆的EI为常数.）(a) (b) (c) (d)图习题8.2利害推断(1)位移法基础已知量的个数与结构的超静定次数无关.（）(2)位移法可用于供解静定结构的内力.（）(3)用位移法估计结构由于收座移动引起的内力时，采与与荷载效率时相共的基础结构.（）(4)位移法只可用于供解连绝梁战刚刚架，不克不迭用于供解桁架.（）习题8.3用位移法估计习题6.6图所示连绝梁，做直矩图战剪力图，EI=常数.(1)(2)习题8.4用位移法估计结构，做直矩图，EI=常数.(1)(2)第9章渐近法习题解问习题9.1利害推断题(1)力矩调配法不妨估计所有超静定刚刚架的内力.（）(2)习题7.1(2)图所示连绝梁的蜿蜒刚刚度为EI，杆少为l，杆端直矩M BC<M.（）习题7.1(2)图习题7.1(3)图(3)习题7.1(3)图所示连绝梁的线刚刚度为i，欲使A端爆收逆时针单位转角，需施加的力矩M A>3i.（）习题9.2挖空题(1)习题7.2(1)图所示刚刚架EI=常数，各杆少为l，杆端直矩M AB =________.(2)习题7.2(2)图所示刚刚架EI=常数，各杆少为l，杆端直矩M AB =________.(3)习题7.2(3)图所示刚刚架各杆的线刚刚度为i，欲使结面B爆收逆时针的单位转角，应正在结面B施加的力矩M B =______.习题7.2(1)图习题7.2(2)图习题7.2(3)图(4)用力矩调配法估计习题7.2(4)图所示结构（EI=常数）时，传播系数C BA =________，C BC =________.习题7.2(4)图习题9.3用力矩调配法估计习题7.3图所示连绝梁，做直矩图战剪力图，并供收座B的反力.（1）（2）习题9.4用力矩调配法估计习题7.4图所示连绝梁，做直矩图.（1）（2）习题9.5用力矩调配法估计习题7.5图所示刚刚架，做直矩图.（1）（2）第11章效率线及其应用习题解问习题11.1利害推断题(1)习题8.1(1)图示结构BC杆轴力的效率线应画正在BC杆上.（）习题8.1(1)图习题8.1(2)图(2) 习题8.1(2)图示梁的M C效率线、F Q C效率线的形状如图（a）、（b）所示.(3) 习题8.1(3)图示结构，利用M C效率线供牢固荷载F P1、F P2、F P3效率下M C的值，可用它们的合力F R去代替，即M C= F P1y1+ F P2y2+ F P3y3=F R y.( )习题8.1(3)图(4) 习题8.1(4)图中的（a）所示主梁F Q C左的效率线如图（b）所示.( )习题8.1(4)图(5)习题8.1(5)图示梁F R A的效率线与F Q A左的效率线相共.( )习题8.1(5)图(6) 简收梁的直矩包络图为活载效率下各截里最大直矩的连线.( )习题11.2挖空题(1) 用静力法做效率线时，其效率线圆程是.用机动法做静定结构的效率线，其形状为机构的.(2) 直矩效率线横目标量目是.(3)习题8.2(3)图所示结构，F P=1沿AB移动，M D的效率线正在B面的横标为，F Q D的效率线正在B面的横标为.习题8.2(3)图(4) 习题8.2(4)图所示结构，F P=1沿ABC移动，则M D 效率线正在B面的横标为.习题8.2(4)图(5)习题8.2(5)图所示结构，F P=1沿AC移动，截里B的轴力F N B的效率线正在C面的横标为.习题8.2(5)图习题11.3单项采用题(1)习题8.3(1)图所示结构中收座A左侧截里剪力效率线的形状为( ).习题8.3(1)图(2) 习题8.3(2)图所示梁止家列荷载效率下，反力F R A的最大值为( ).(a) 55kN (b) 50kN (c) 75kN (d) 90kN习题8.3(2)图(3)习题8.3(3)图所示结构F Q C效率线(F P=1正在BE上移动)BC、CD段横标为( ).(a) BC,CD均不为整； (b) BC,CD均为整；(c) BC为整,CD不为整；(d) BC不为整,CD为整.习题8.3(3)图(4)习题8.3(4)图所示结构中，收座B左侧截里剪力效率线形状为( ).习题8.3(4)图(5)习题8.3(5)图所示梁止家列荷载效率下，截里K的最大直矩为( ).(a) 15kN·m(b) 35 kN·m(c) 30 kN·m(d) kN·m习题8.3(5)图习题11.4做习题8.4(a)图所示悬臂梁F R A、M C、F Q C的效率线.习题11.5做习题8.5(a)图所示结构中F N BC、M D的效率线，F P =1正在AE上移动.习题11.6做习题8.6(a)图所示伸臂梁的M A、M C、F Q A 左、F Q A左的效率线.习题11.7做习题8.7(a)图所示结构中截里C的M C、F Q C的效率线.习题11.8(a)图所示静定多跨梁的F R B、M E、F Q B左、F Q B左、F Q C的效率线.习题11.9(a)图所示牢固荷载效率下截里K的内力M K战F Q K左.习题11.10(a)图所示连绝梁M K、M B、F Q B左、F Q B左效率线的形状.若梁上有随意安插的均布活荷载，请画出使截里K爆收最大直矩的荷载安插.第2章仄里体系的机动领会习题解问习题利害推断题(1) 若仄里体系的本质自由度为整，则该体系一定为几许稳定体系.( )(2) 若仄里体系的估计自由度W=0，则该体系一定为无多余拘束的几许稳定体系.( )(3) 若仄里体系的估计自由度W＜0，则该体系为有多余拘束的几许稳定体系.( )(4) 由三个铰二二贯串的三刚刚片组成几许稳定体系且无多余拘束.( )(5) 习题2.1(5) 图所示体系去掉二元体CEF后，结余部分为简收刚刚架，所以本质系为无多余拘束的几许稳定体系.( )习题 2.1(5)图(6) 习题2.1(6)(a)图所示体系去掉二元体ABC后，成为习题2.1(6) (b)图，故本质系是几许可变体系.( )(7) 习题2.1(6)(a)图所示体系去掉二元体EDF后，成为习题2.1(6) (c)图，故本质系是几许可变体系.( )习题 2.1(6)图【解】（1）精确.（2）过失.0W 是使体系成为几许稳定的需要条件而非充分条件.（3）过失.（4）过失.惟有当三个铰不共线时，该题的论断才是精确的.（5）过失.CEF不是二元体.（6）过失.ABC不是二元体.（7）过失.EDF不是二元体.习题挖空(1) 习题2.2(1)图所示体系为_________体系.习题2.2(1)图(2) 习题2.2(2)图所示体系为__________体系.习题 2-2(2)图(3) 习题2.2(3)图所示4个体系的多余拘束数目分别为_______、________、__________、__________.习题 2.2(3)图(4) 习题 2.2(4)图所示体系的多余拘束个数为___________.习题 2.2(4)图(5) 习题 2.2(5)图所示体系的多余拘束个数为___________.习题 2.2(5)图(6) 习题 2.2(6)图所示体系为_________体系，有_________个多余拘束.习题 2.2(6)图(7) 习题 2.2(7)图所示体系为_________体系，有_________个多余拘束.习题 2.2(7)图【解】（1）几许稳定且无多余拘束.安排二边L形杆及大天分别动做三个刚刚片.（2）几许常变.中间三铰刚刚架与大天形成一个刚刚片，其与左边倒L形刚刚片之间惟有二根链杆相联，缺少一个拘束.（3）0、1、2、3.末尾一个启关的圆环（大概框）里里有3个多余拘束.（4）4.表层可瞅做二元体去掉，下层多余二个铰.（5）3.下层（包罗大天）几许稳定，为一个刚刚片；与表层刚刚片之间用三个铰相联，多余3个拘束.（6）里里几许稳定、0.将左上角火仄杆、左上角铰交三角形战下部铰交三角形分别动做刚刚片，根据三刚刚片准则领会.（7）里里几许稳定、3.中围启关的正圆形框为有3个多余拘束的刚刚片；里里铰交四边形可选一对付仄止的对付边瞅做二个刚刚片；根据三刚刚片准则即可领会.对付习题2.3图所示各体系举止几许组成领会.【解】（1）如习题解2.3(a)图所示，刚刚片AB与刚刚片I 由铰A战收杆①相联组成几许稳定的部分；再与刚刚片BC 由铰B战收杆②相联，故本质系几许稳定且无多余拘束.习题解2.3(a)图（2）刚刚片Ⅰ、Ⅱ、Ⅲ由不共线三铰A、B、（Ⅰ，Ⅲ）二二相联，组成几许稳定的部分，如习题解2.3(b)图所示.正在此部分上增加二元体C-D-E，故本质系几许稳定且无多余拘束.习题解2.3(b)图（3）如习题解2.3(c)图所示，将左、左二端的合形刚刚片瞅成二根链杆，则刚刚片Ⅰ、Ⅱ、Ⅲ由不共线三铰（Ⅰ，Ⅱ）、（Ⅱ，Ⅲ）、（Ⅰ，Ⅲ）二二相联，故体系几许稳定且无多余拘束.习题解2.3(c)图（4）如习题解2.3(d)图所示，刚刚片Ⅰ、Ⅱ、Ⅲ由不共线的三铰二二相联，产死大刚刚片；该大刚刚片与天基之间由4根收杆贯串，有一个多余拘束.故本质系为有一个多余拘束的几许稳定体系.习题解2.3(d)图（5）如习题解2.3(e)图所示，刚刚片Ⅰ、Ⅱ、Ⅲ组成几许稳定且无多余拘束的体系，为一个大刚刚片；该大刚刚片与天基之间由仄止的三根杆①、②、③相联，故本质系几许瞬变.习题解2.3(e)图（6）如习题解2.3(f)图所示，由三刚刚片准则可知，刚刚片Ⅰ、Ⅱ及天基组成几许稳定且无多余拘束的体系，设为夸大的天基.刚刚片ABC与夸大的天基由杆①战铰C相联；刚刚片CD与夸大的天基由杆②战铰C相联.故本质系几许稳定且无多余拘束.习题解2.3(f)图第3章静定梁与静定刚刚架习题解问习题利害推断题(1) 正在使用内力图特性画制某受直杆段的直矩图时，必须先供出该杆段二端的端直矩.（）(2) 区段叠加法仅适用于直矩图的画制，不适用于剪力图的画制.（）(3) 多跨静定梁正在附属部分受横背荷载效率时，必会引起基础部分的内力.（）(4) 习题3.1(4)图所示多跨静定梁中，CDE战EF部分均为附属部分.（）习题3.1(4)图【解】（1）精确；（2）过失；（3）精确；（4）精确；EF为第二条理附属部分，CDE为第一条理附属部分；习题挖空(1)习题3.2(1)图所示受荷的多跨静定梁，其定背通联C所传播的直矩M C的大小为______；截里B的直矩大小为______，____侧受推.习题3.2(1)图(2) 习题3.2(2)图所示风载效率下的悬臂刚刚架，其梁端直矩M AB=______kN·m，____侧受推；左柱B截里直矩M B=______kN·m，____侧受推.习题3.2(2)图【解】（1）M C = 0；M C = F P l，上侧受推.CDE部分正在该荷载效率下自仄稳；（2）M AB=288kN·m，左侧受推；M B=32kN·m，左侧受推；习题做图所示单跨静定梁的M图战F图.Q(a) (b)(c) (d)(e) (f)【解】M图（单位：kN·m）F Q图（单位：kN）(a)M图F Q图(b)M图F Q 图(c)M图F Q图(d)M图F Q图(e)M图（单位：kN·m）F Q图（单位：kN）(f)习题做图所示单跨静定梁的内力图.(c) 【解】M图（单位：kN·m）F Q图（单位：kN）(c)习题做图所示斜梁的内力图.【解】M图（单位：kN·m）F Q图（单位：kN）F N图（单位：kN）习题做图所示多跨梁的内力图.(a)【解】M图（单位：kN·m）F Q图（单位：kN）(a)习题3.7 改正图所示刚刚架的直矩图中的过失部分.(a) (b) (c)(d) (e) (f)【解】(a) (b) (c)(d) (e) (f)习题做图所示刚刚架的内力图.(a)(b)【解】M图（单位：kN·m）F Q图（单位：kN）F N图（单位：kN）(a)M图（单位：kN·m）F Q图（单位：kN）F N图（单位：kN）(b)第4章静定拱习题解问习题4.1利害推断题(1) 三铰拱的火仄推力不但是与三个铰的位子有关，还与拱轴线的形状有关.（）(2) 所谓合理拱轴线，是指正在任性荷载效率下皆能使拱处于无直矩状态的轴线. （）(3) 改变荷载值的大小，三铰拱的合理拱轴线形状也将爆收改变. （ ） 【解】（1）过失.从公式0H /C F M f =可知，三铰拱的火仄推力与拱轴线的形状无关；（2）过失.荷载爆收改变时，合理拱轴线将爆收变更； （3）过失.合理拱轴线与荷载大小无关； 习题4.2挖空(1) 习题3.2(3)图所示三铰拱的火仄推力F H 等于.习题3.2(3)图【解】（1）F P /2；习题4.3供图所示三铰拱收反力战指定截里K 的内力.已知轴线圆程24()fy x l x l=-.【解】H H 16kN A B F F ==;VA 8kN()F =↑;V 24kN()B F =↑ 15kN m K M =-⋅;Q 1.9kN K F =;N 17.8kN K F =-第5章 静定仄里桁架习题解问习题5.1 利害推断题(1) 利用结面法供解桁架结构时，可从任性结面启初. （ ） 【解】（1）过失.普遍从仅包罗二个已知轴力的结面启初. 习题5.2挖空(1)习题3.2(4)图所示桁架中有根整杆.习题3.2(4)图【解】（1）11（仅横背杆件中有轴力，其余均为整杆）. 习题5.3 试用结面法供图所示桁架杆件的轴力.(a) (b)【解】 (1)提示：根据整杆判别规则有：N13N430F F ==；根据等力杆判别规则有：N24N46F F =.而后分别对付结面2、3、5列力仄稳圆程，即可供解局部杆件的内力. (2) 提示：根据整杆判别规则有：N18N17N16N27N36N450F F F F F F ======；根据等力杆判别规则有：N12N23N34F F F ==；N78N76N65F F F ==.而后与结面4、5列力仄稳圆程，即可供解局部杆件的内力.习题5.4 推断图所示桁架结构的整杆.(a) (b) (c)【解】(a) (b) (c)提示：(c)题需先供出收座反力后，截与Ⅰ.Ⅰ截里以左为断绝体，由30M =∑，可得N120F =，而后再举止整杆推断. 习题5.5 用截里法供解图所示桁架指定杆件的轴力.(a)(b)【解】(1) N P 32a F F =-；N P 12b F F =；N Pc F F =提示：截与Ⅰ.Ⅰ截里可得到N b F 、N c F ；根据整杆推断规则，杆26、杆36为整杆，则通过截与Ⅱ.Ⅱ截里可得到N a F . (2)N 0a F =；N P b F =；N 0c F =提示：截与Ⅰ.Ⅰ截里可得到N b F ；由结面1可知N 0a F =；截与Ⅱ.Ⅱ截里，与圆圈以内为摆脱体，对付2面与矩，则N 0c F =.第6章 结构的位移估计习题解问习题6.1 利害推断题(1) 变形骸真功本理仅适用于弹性体系，不适用于非弹性体系.（ ）(2) 真功本理中的力状态战位移状态皆是真设的.（ ）(3) 功的互等定理仅适用于线弹性体系，不适用于非线弹性体系.（ ）(4) 反力互等定理仅适用于超静定结构，不适用于静定结构.（ ）(5) 对付于静定结构，有变形便一定有内力.（ ） (6) 对付于静定结构，有位移便一定有变形.（ ） (7) 习题4.1(7)图所示体系中各杆EA 相共，则二图中C 面的火仄位移相等.（ ）(8) M P 图，M 图如习题4.1(8)图所示，EI =常数.下列图乘截止是精确的：4)832(12l l ql EI ⨯⨯⨯ （ ）(9) M P 图、M (9)图所示，下列图乘截止是精确的：033202201111)(1y A EI y A y A EI ++ （ ）(10) (10)图所示结构的二个仄稳状态中，有一个为温度变更，此时功的互等定理不可坐.（ ） 习题 4.1(7)图习题 4.1(8)图 习题 4.1(9)图习题 4.1(10)图【解】（1）过失.变形骸真功本理适用于弹性战非弹性的所有体系.（2）过失.惟有一个状态是真设的. （3）精确.（4）过失.反力互等定理适用于线弹性的静定战超静定结构.（5）过失.譬如静定结构正在温度变更效率下，有变形但是不内力.（6）过失.譬如静定结构正在收座移动效率下，有位移但是稳定形.（7）精确.由桁架的位移估计公式可知.（8）过失.由于与0y 的M 图为合线图，应分段图乘.（9）精确. （10）精确.习题6.2挖空题(1) 习题4.2(1)图所示刚刚架，由于收座B 下重所引起D 面的火仄位移D H =______.(2) 真功本理有二种分歧的应用形式，即_______本理战_______本理.其中，用于供位移的是_______本理.(3) 用单位荷载法估计位移时，假制状态中所加的荷载应是与所供广义位移相映的________.(4) 图乘法的应用条件是：__________且M P 与M 图中起码有一个为直线图形.(5) 已知刚刚架正在荷载效率下的M P 图如习题4.2(5)图所示，直线为二次扔物线，横梁的抗直刚刚度为2EI ，横杆为EI ，则横梁中面K 的横背位移为________.(6) 习题4.2(6)图所示拱中推杆AB 比本安排少度短了，由此引起C 面的横背位移为________；引起收座A 的火仄反力为________.(7) 习题4.2(7)图所示结构，当C 面有F P =1(↓)效率时，D 面横背位移等于(↑)，当E 面有图示荷载效率时，C 面的横背位移为________.(8) 习题 4.2(8)图（a ）所示连绝梁收座B 的反力为)(1611R ↑=B F ，则该连绝梁正在收座B 下重B =1时（如图（b ）所示），D 面的横背位移Dδ=________.习题 4.2(1)图 习题 4.2(5)图习题 4.2(6)图 习题 4.2(7)图习题 4.2(8)图【解】（1）()3∆→.根据公式R ΔF c =-∑估计.（2）真位移、真力；真力 . （3）广义单位力.（4）EI 为常数的直线杆.（5）48.875()EI↓.先正在K 面加单位力并画M 图，而后利用图乘法公式估计.（6）1.5cm ↑；0.C 面的横背位移用公式NΔF l =∆∑估计；制制缺面不会引起静定结构爆收反力战内力.（7）()a∆↑.由位移互等定理可知，C 面效率单位力时，E面沿M 目标的位移为21a∆δ=-.则E 面效率单位力M =1时，C面爆收的位移为12a∆δ=-.（8）11()16↓.对付（a ）、（b ）二个图示状态，应用功的互等定理可得截止.C V .EI为常数.【解】1）供C V习题4.3(1)图（1） 积分法画M P 图，如习题4.3（1）(b)图所示.正在C 面加横背单位力F P =1，并画M 图如习题4.3（1）(c)图所示.由于该二个直矩图对付称，可估计一半，再将截止乘以2.AC 段直矩为12M x =，P P 12M F x =则（2） 图乘法 2)供C V习题4.3(2)图（1） 积分法画M P 图，如习题4.3（2）(b)图所示.正在C 面加横背单位力并画M 图，如习题4.3（2）(c)图所示.以C 面为坐标本面，x 轴背左为正，供得AC 段（0≤x ≤2）直矩为M x =，2P 10(2)M x =⨯+则（2） 图乘法由估计位移的图乘法公式，得3)供C V习题4.3(3)图（1） 积分法画M P 图，如习题4.3（3）(b)图所示.正在C 面加横背单位力并画M 图，如习题4.3（3）(c)图所示.根据图中的坐标系，二杆的直矩（按下侧受推供）分别为 AB 杆12M x =-，2P 142ql M x qx =-CB 杆M x =，P 2ql M x =则（2）图乘法 4)供A习题4.3（4）图（1）积分法画M P 图，如习题4.3（4）(b)图所示.正在A 面加单位力奇并画M 图，如习题4.3（4）(c)图所示.以A 为坐标本面，x 轴背左为正，直矩表白式（以下侧受推为正）为113M x l=-，2P 3122M qlx qx =-则358ql EI=（ ） （2） 图乘法由估计位移的图乘法公式，得358ql EI=（ ） 分别用积分法战图乘法供习题 4.4(a)图所示刚刚架C 面的火仄位移C H .已知EI =常数.【解】1）积分法P M 、M图分别如习题 4.4（b ）、（c ）图所示，修坐坐标系如（c ）图所示.各杆的直矩用x 表示，分别为 CD 杆M x =，P 12M qlx =AB 杆M x =，2P 12M qlx qx =-代进公式估计，得2）图乘法习题 4.5(a)图所示桁架各杆截里均为A =2×103m 2，E ×108kN/m 2，F P =30kN ，d =2m.试供C 面的横背位移V C ∆.D ql lBAC lA B lD CABD C22ql 2ql281ql 2(b)图M P M 图(c)(a)xx1ll【解】画NP F 图，如习题4.5(b)图所示.正在C 面加横背单位力，并画N F 图，如习题4.5(c)图所示. 由桁架的位移估计公式N NP F F Δl EA=∑，供得 第7章 力法习题解问利害推断题（1）习题5.1(1)图所示结构，当收座A 爆收转化时，各杆均爆收内力.（ ）习题5.1(1)图习题5.1(2)图（2）习题 5.1(2)图所示结构，当内中侧均降下t 1℃时，二杆均只爆收轴力.（ ）（3）习题 5.1(3)图(a)战(b)所示二结构的内力相共.（ ）习题5.1(3)图（4）习题 5.1(3)图(a)战(b)所示二结构的变形相共.（ ）【解】（1）过失.BC 部分是静定的附属部分，爆收刚刚体位移，而无内力.（2）过失.刚刚结面会沿左上圆爆收线位移，从而引起所连梁柱的蜿蜒.（3）精确.二结构中梁二跨的抗直刚刚度比值均为1:1，果此二结构内力相共.（4）过失.二结构内力相共，但是图(b)结构的刚刚度是图(a)的一倍，所以变形惟有图(a)的一半.习题7.2 挖空题（1）习题5.2(1) 图(a)所示超静定梁的收座A 爆收转角，若选图(b)所示力法基础结构，则力法圆程为_____________，代表的位移条件是______________，其中1c =_________；若选图(c)所示力法基础结构时，力法圆程为____________，代表的位移条件是______________，其中1c =_________.习题5.2(1)图（2）习题5.2(2)图(a)所示超静定结构，当基础体系为图(b)时，力法圆程为____________________，1P =________；当基础体系为图(c)时，力法圆程为____________________，1P =________.习题5.2(2)图（3）习题5.2(3)图(a)所示结构各杆刚刚度相共且为常数，AB 杆中面直矩为________，____侧受推；图(b)所示结构M BC =________，____侧受推.习题5.2(3)图（4）连绝梁受荷载效率时，其直矩图如习题5.2(4)图所示，则D 面的挠度为________，位移目标为____.习题5.2(4)图【解】（1）1111c 0X δ∆+=，沿X 1的横背位移等于整，－2l ；1111c X δ∆θ+=，沿X 1的转角等于，0.（2）11111P X X k δ∆+=-，458ql EI -；1111P 0X δ∆+=，3242ql q EI k+. （3）28ql ，下侧；2M ，下侧.可利用对付称性简化估计. （4）52EI，背下.选三跨简收梁动做基础结构，正在其上D 面加横背单位力并画M 图，图乘即可.试决定习题5.3图所示结构的超静定次数.图【领会】结构的超静定次数等于其估计自由度的千万于值，大概者使用“排除多余拘束法”直交领会.【解】（a ）1；（b ）2；（c ）5；（d ）3.用力法估计习题5.4图所示各超静定梁，并做出直矩图战剪力图.图【解】（1）本结构为1次超静定结构.采用基础体系如习题解5.4(1)图(a)所示，基础圆程为1111P 0X δ∆+=.系数战自由项分别为114EI δ=，1P 54EI∆=- 解得113.5kN m X =⋅.直矩图战剪力图分别如习题解5.4(1)图(d)战(e)所示. 习题解5.4(1)图用力法估计习题5.5图所示各超静定刚刚架，并做出内力图.图【解】（3）本结构为2次超静定结构.采用基础体系如习题解5.5(3)图(a)所示，基础圆程为系数战自由项分别为112503EI δ=，12210δδ==，226083EI δ=，1P 625EI ∆=，2P 20003EI∆= 解得17.5kN X =-，2 3.29kN X =-.内力图分别如习题解 5.5(3)图(e)~(g)所示. 习题解5.5(3)图利用对付称性，估计习题5.12图所示各结构的内力，并画直矩图.图【解】（2）将本结构所受普遍荷载领会为对付称战阻挡。

第四章 力法4-1 利用对称与反对称条件，简化图4-15所示各平面刚架结构，要求画出简化图及其位移边界条件。

(a)(a)解：对称结构，在对称载荷作用下，在对称轴上反对称内力为零。

由静力平衡条件∑=0X可得23PN =再由两个静力平衡条件，剩余4个未知力，为二次静不定。

本题中通过对称性条件的使用，将6次静不定的问题转化为2次静不定。

PP(b)(b)解：对称结构，在反对称载荷作用下，在对称轴上对称的内力为零。

受力分析如图所示有2根对称轴，结合平衡方程，剩下三个未知数，为3次静不定。

本题中通过对称性条件的使用，将6次静不定问题转化为3次静不定。

(c)(c)解：对称结构，在对称载荷作用下，在对称轴上反对称内力为零。

有一根对称轴，减少了两个静不定度本题中通过对称性条件的使用，将3次静不定问题转化为1次静不定。

4-2图4-16所示桁架各杆的EA均相同，求桁架各杆的内力。

(a)(a)解：1、分析结构静不定次数。

结构有4个结点8个自由度，6根杆6个约束，3个外部约束。

因此结构静不定次数为1，f=1。

2、取基本状态。

切开2-4杆，取<P>,<1>状态，各杆内力如图。

1234P-P √2P<P>1234P<1>11√22√22√22√22计算影响系数∑=∆EAl N N i p P 11()2422222+=⎪⎪⎭⎫ ⎝⎛⨯+⨯=EA Pa P P EA a ∑=EAl N i1211δ()22222142222+=⎪⎪⎭⎫ ⎝⎛⨯⨯+⨯⨯=EA a EA a 列正则方程：()()02242221=+++P X解之()P X 42321-=3、由11N X N N P +=，得()P X N 423220112-=⎪⎪⎭⎫ ⎝⎛-⋅+= ()P X P N 42212113+=⋅+=()P X N 423220114-=⎪⎪⎭⎫ ⎝⎛-⋅+=()P X N 423220123-=⎪⎪⎭⎫ ⎝⎛-⋅+=()P X N 423210124-=⋅+=()P X P N 42122134+-=⎪⎪⎭⎫ ⎝⎛-⋅+-=4、校核。

第1章绪论（无习题）第2章平面体系的机动分析习题解答习题2.1是非判断题(1) 若平面体系的实际自由度为零，则该体系一定为几何不变体系。

( )(2) 若平面体系的计算自由度W=0，则该体系一定为无多余约束的几何不变体系。

( )(3) 若平面体系的计算自由度W＜0，则该体系为有多余约束的几何不变体系。

( )(4) 由三个铰两两相连的三刚片组成几何不变体系且无多余约束。

( )(5) 习题2.1(5) 图所示体系去掉二元体CEF后，剩余部分为简支刚架，所以原体系为无多余约束的几何不变体系。

( )习题2.1(5)图(6) 习题2.1(6)(a)图所示体系去掉二元体ABC后，成为习题2.1(6) (b)图，故原体系是几何可变体系。

( )(7) 习题2.1(6)(a)图所示体系去掉二元体EDF后，成为习题2.1(6) (c)图，故原体系是几何可变体系。

()(a)(b)(c)习题2.1(6)图习题2.2填空(1) 习题2.2(1)图所示体系为_________体系。

习题2.2(1)图(2) 习题2.2(2)图所示体系为__________体系。

习题2-2(2)图(3) 习题2.2(3)图所示4个体系的多余约束数目分别为_______、________、__________、__________。

习题2.2(3)图(4) 习题2.2(4)图所示体系的多余约束个数为___________。

习题 2.2(4)图(5) 习题2.2(5)图所示体系的多余约束个数为___________。

习题 2.2(5)图(6) 习题2.2(6)图所示体系为_________体系，有_________个多余约束。

习题 2.2(6)图(7) 习题2.2(7)图所示体系为_________体系，有_________个多余约束。

习题 2.2(7)图习题2.3 对习题2.3图所示各体系进行几何组成分析。

(a)(b)(c)(d)(e)(f)(h)(g)(i)(j)(k)(l)习题2.3图第3章 静定梁与静定刚架习题解答习题3.1 是非判断题(1) 在使用力图特征绘制某受弯杆段的弯矩图时，必须先求出该杆段两端的端弯矩。

第三章 静定结构的位移计算一、判断题：1、虚位移原理等价于变形谐调条件，可用于求体系的位移。

2、按虚力原理所建立的虚功方程等价于几何方程。

3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下，静定结构不产生内力，但会有位移且位移只与杆件相对刚度有关。

4、求图示梁铰C 左侧截面的转角时，其虚拟状态应取：A.;; B.D.C.M =15、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。

6、已知M p 、M k 图，用图乘法求位移的结果为：()/()ωω1122y y EI +。

M k M p7、图a 、b 两种状态中，粱的转角ϕ与竖向位移δ间的关系为：δ=ϕ 。

8、图示桁架各杆E A 相同，结点A 和结点B 的竖向位移均为零。

9、图示桁架各杆EA =常数，由于荷载P 是反对称性质的，故结点B 的竖向位移等于零。

二、计算题：10、求图示结构铰A 两侧截面的相对转角ϕA ，EI = 常数。

q l l l /211、求图示静定梁D 端的竖向位移∆DV 。

EI = 常数，a = 2m 。

a a a 10kN/m12、求图示结构E 点的竖向位移。

EI = 常数。

l l l /3/3q13、图示结构，EI=常数，M =⋅90kN m , P = 30kN 。

求D 点的竖向位移。

P 3m 3m 3m14、求图示刚架B 端的竖向位移。

ql15、求图示刚架结点C 的转角和水平位移，EI = 常数。

16、求图示刚架中Ｄ点的竖向位移。

EI＝常数。

l/217、求图示刚架横梁中Ｄ点的竖向位移。

EI ＝常数。

18、求图示刚架中D 点的竖向位移。

E I = 常数 。

ql l/219、求图示结构Ａ、Ｂ两截面的相对转角，EI ＝常数。

l/23l/320、求图示结构A 、B 两点的相对水平位移，E I = 常数。

l l21、求图示结构B 点的竖向位移，EI =常数。

l l22、图示结构充满水后，求A 、B 两点的相对水平位移。

飞行器结构力学基础李亚智航空学院·航空结构工程系第4章力法4.1 概述静不定（超静定）结构具有“多余”未知力。

多余未知力（内力或支反力）是由多余约束引起的，也叫做多余约束力。

静不定结构中的多余未知力不能仅由平衡条件求出，而必须引入变形协调条件后才能求解。

力法是计算静不定结构内力和位移的一种基本方法。

力法的基本未知量是力—多余未知力。

4.2 力法原理及力法典型方程力法计算的基本思路：把静不定结构的计算问题转化为静定结构的计算问题，即利用静定结构的计算方法来达到求解静不定结构的目的。

P例1、图示三支点梁A B C一次静不定，有一个多余约束。

B AC P X（2）把多余约束对梁的作用（约束力）用集中力X 表示。

（1）先去掉一个多余约束（譬如可动铰支座B ）。

材料力学的求解方法：去掉多余约束后所得到的静定结构称为力法的基本系统。

本例的基本系统就是一根简支梁。

X 就是多余未知力（多余约束力），只要知道它的大小，就可以应用平衡条件求出原结构系统的支反力和内力（剪力和弯矩）的大小与分布。

A C PB 原系统基本系统A B C PAC X BX∆（3）借助变形几何关系求解多余未知力上式即为力法求解的典型方程（正则方程）。

变形几何关系：0=∆+∆=∆X P B 令为仅在X = 1作用下其作用点的位移，则1δX X ⋅=∆1δ变形几何关系成为：1=⋅+∆X P δA C PB P∆0=∆BP 1P 212例2、二次静不定桁架，共11根杆。

基本系统以两个斜杆1和2的内力作为多余未知力。

解：将两杆切开，等于去掉了两个多余约束，变成静定结构，也就是构成一个基本系统。

12原系统=++P 1P 212原状态P 1P 2载荷状态X 1多余未知力状态1X 2多余未知力状态2外载荷和多余未知力均可看作是作用于基本系统上的外力。

上页图中有以下几层含义：•原结构中多余未知力X1和X2是被动力（由外力引起），而在基本系统中是以主动力（外力）的形式出现的。

静定结构的位移计算习题4—1 (a)用单位荷载法求图示结构B 点的水平位移解：1. 设置虚拟状态选取坐标如图。

2. M P 图和 如图示3. 虚拟状态中各杆弯矩方程为实际状态中各杆弯矩方程为M P =F P x4. 代入公式（4—6）得 △BH =l实际状态1虚拟状态5F P l 15l M P 图图M 图M xM =141012118111EI F EI x F x EI x F x EI dx M M P l l P l P P =⨯⨯+⨯⨯=∑⎰⎰⎰(←)4—1 (b)单位荷载法求图示刚架B 点的水平位移 解：1. 设置虚拟状态选取坐标如图。

2. M P 图和 如图示3. 虚拟状态中各杆弯矩方程为 BD: DC: CA: 实际状态中各杆弯矩方程为 BD: M P =0 DC: M P =40x CA: M P =160+5x 24. 代入公式（4—6）得图M x M =3=M xM-=3△BH =4—2试求图示桁架结点B 的竖向位移，已知桁架各杆的EA =21×104KN 。

1M P 图M 3KN •m340KN •m3KN •m3KN •m)(833.05160)3(40306012401301←=+⨯-+⨯+*=∑⎰⎰⎰⎰cm EI x x x EI x EI x EI dxM M P实际状态虚拟状态解：虚拟状态如图示。

实际状态和虚拟状态所产生的杆件内力均列在表4—1中，根据式4—7可得结点B的竖向位移为表4—1中)(768.010215.16124↓=⨯∙=∆cm KNm KN BV4—3 （a）、（b）试用图乘法求图示结构B 处的转角和C 处的竖向位移。

EI=常数。

M=ql 2M P 图ql 2/81M=1（a ）解：M P 图、单位力偶下作用于B 点的1M 图、单位力下作用于C 点的2M 图EIql ql l ql l EI B 3)21223232221(1222=⨯⨯⨯-⨯⨯⨯=ϕ（ ）（b ）解：M P 图、单位力偶下作用于B 点的1M 图、单位力作用于C 点的2M 图)2183232421(122⨯⨯⨯-⨯⨯⨯=ql l l ql EI B ϕ=ql 3/24EI( ))23242212832232421(1222ql ql l ql ql l ql l ql EI cv ⨯⨯⨯⨯+⨯⨯⨯-⨯⨯⨯⨯=∆)(24)2852232322213221(14222↑-=⨯⨯⨯⨯⨯+⨯⨯⨯-⨯⨯⨯-=∆EI qll ql l ql l l ql l l EI CV= ql4/24EI(↓)（b）ql/2ql2/4l/2（C ）解：M P 图、单位力偶作用于B 点的1M 图、单位力作用于C 点时的2M 图EIl F lF ll EI P P B 12231211322121(12=⨯⨯⨯⨯+⨯⨯⨯⨯-=ϕ( )ll)(12231212232221(12↓=⨯⨯⨯⨯+⨯⨯⨯⨯⨯-=∆EIl F lF l l l F l l EI P P P cv 4—4 （a ）试求图示结构C 点的竖向位移。

第四章 平面机构的力分析题4-7机械效益Δ是衡量机构力放大程度的一个重要指标，其定义为在不考虑摩擦的条件下机构的输出力（力矩）与输入力（力矩）之比值，即Δ=d r d r F F M M //=。

试求图示各机构在图示位置时的机械效益。

图a 所示为一铆钉机，图b 为一小型压力机，图c 为一剪刀。

计算所需各尺寸从图中量取。

（a ） (b) (c)解：(a)作铆钉机的机构运动简图及受力 见下图（a ）由构件3的力平衡条件有：02343=++R R rF F F由构件1的力平衡条件有：04121=++d R R按上面两式作力的多边形见图（b ）得θcot ==∆d r F F（b ）作压力机的机构运动简图及受力图见（c ）由滑块5的力平衡条件有：04565=++R R F F G由构件2的力平衡条件有：0123242=++R R R 其中 5442R R =按上面两式作力的多边形见图（d ），得tF G =∆(c) 对A 点取矩时有 b F a F d r ⋅=⋅ab =∆其中a 、b 为F r 、F d 两力距离A 点的力臂。

tF G =∆(d)(a)(b)drR41F R43F dG题4-8在图示的曲柄滑块机构中，设已知l AB=0.1m，l BC=0.33m，n1=1500r/min（为常数），活塞及其附件的重量G3=21N，连杆质量G2=25N，J S2=0.0425kg·m2，连杆质心S2至曲柄销B的距离l BS2=l BC/3。

试确定在图示位置时活塞的惯性力以及连杆的总惯性力。

解：1) 选定比例尺, mmml005.0=μ绘制机构运动简图。

(图(a) )2）运动分析：以比例尺vμ作速度多边形，如图(b)以比例尺aμ作加速度多边形如图4-1 (c)244.23smcpaaC=''=μ2222100smspaaS=''=μ22215150sBCcnlalaBCtBC=''==μμα3) 确定惯性力活塞3：)(37673333NagGamFCSI=-=-=方向与cp''相反。

西工大2021年4月机考《结构力学》作业试卷总分:100 得分:100答案网叫福到（这四个字的拼音）一、单选题(共20 道试题,共40 分)1.三铰拱的合理轴线为（）。

A.任意荷载下均为合理轴线B.确定荷载下且跨度给定时为合理轴线C.合理轴线的跨度可以任意D.合理轴线时弯矩为零，但剪力不一定为零正确答案:B2.两个共点力可合成一个力，一个力也可分解为两个相交的力。

一个力分解为两个相交的力可以有（）。

A.一个B.两个C.几个D.无穷多3.在力学上把大小相等、方向相反、作用线相互平行的两个力，称为（）。

A.力矩B.力偶C.合力D.平衡力4.在径向均布荷载作用下，三铰拱的合理轴线为（）。

A.圆弧线B.抛物线C.悬链线D.正弦曲线5.三个刚片用（）相连，组成的体系内部几何不变且无多余约束。

A.不互相平行的三根链杆B.六个链杆C.不在同一直线上的三个铰D.不互相平行也不汇交的三链杆6.断开一个刚节点相当于去掉（）个约束。

A.1C.3D.47.三刚片用三个单铰连接，当三个单铰共线时体系为（）。

A.几何可变体系B.几何不变体系C.瞬变体系D.不能确定8.图示多跨静定梁，其基本部分为（）。

A.AB部分B.BC部分C.CD部分D.AB和CD部分9.图示桁架的零杆数目是（）。

A.6B.7C.8D.910.平衡力系是指（）的力系。

A.约束力等于零B.合力等于零C.主动力为零D.合力不为零11.用力法解图所示结构未知量个数是（）。

A.5个B.6个C.9个D.12个12.平面内一点的自由度等于（）。

A.1B.2D.413.A.AB部分B.BC部分C.CD部分D.AB和CD部分14.力法方程实质上是（）条件。

A.位移协调B.平衡C.位移D.变形15.断开一个铰相当于去掉（）个约束。

A.1B.2C.3D.416.力对物体的作用效果取决于（）。

A.力的大小B.力的方向C.力的作用点D.力的大小、方向和作用点17.结构力学将（）作为主要研究对象。