薄膜干涉等厚条纹等倾条纹

17_04 薄膜干涉 —— 等倾干涉1 薄膜等倾干涉折射率为2n ，厚度为h 的薄膜放在折射率为1n 的介质中（12n n <），单色光照射薄膜时，光在上下两个介质面反射后形成两束反射光。

这两束光是从介面同一点A 点分开产生，具有相同的相位，为相干光。

两束光经过不同路径相遇后，发生干涉。

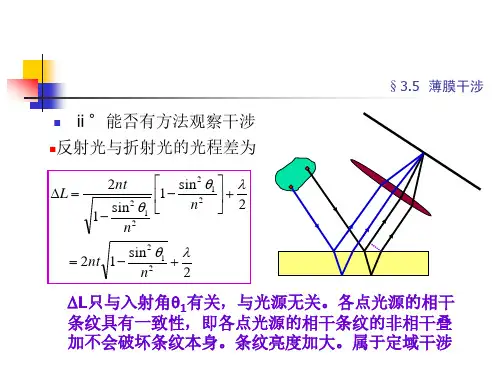
具体可以用一个会聚透镜将两束平行相干光会聚到焦点上，如图XCH004_058所示。

光束1和光束2在透镜焦点S '相遇时的光程差：2121()n AB BC n AD δ=∆-∆=+- —— CD 两点到焦点的光程相等 应用折射定律，同时考虑到半波损失：222cos 2n h i λδ=+—— 上表面的反射光有半波损失，下表面的反射光没有—— S '点的光强I 的取决于两束光的光程差—— 亮条纹和暗条纹满足的条件 2221,2,3,22cos 2(21)1,2,3,2k k n h i k k λλδλ⎧⋅=⎪⎪=+=⎨⎪+⋅=⎪⎩ 干涉相长干涉相消 —— 入射光角度相同的光具有相同的光程差，在相遇点的干涉光强相同2 增透膜和反射膜1) 增透膜 光学玻璃表面蒸镀一层薄膜减少光的反射 —— 增透膜例题01 在照相机的镜头上镀一层MgF 2薄膜，要使该薄膜对550nm λ=的光反射最小，问薄膜的最小厚度为多少？（增透膜），如图XCH004_060所示。

垂直入射时，两个表面反射光的反射光均有半波损失，两束反射在薄膜表面光相遇时的光程差： 22n d δ=要使反射光最小，光程差满足：22(21)0,1,2,32n h k k λδ==+= 镀膜的最小厚度：21004min h nm n λ== —— 0k =—— 如果MgF 2薄膜的折射率23n n > 光程差：222n h λδ=+ —— 存在半波损失要使反射光最小，光程差满足：22(21)0,1,2,322n h k k λλ+=+=22n h k λ=，镀膜的最小厚度：22002min h nm n λ==2) 反射膜 光学玻璃表面蒸镀一层薄膜增加光的反射 —— 反射膜(例如在激光谐振腔的反射镜)例题12 用白光垂直照射置于空气中厚度0.50h mm =的玻璃片。

求等倾干涉条纹公式等倾干涉是光学中一个比较重要的概念，要求等倾干涉条纹公式，咱们得先搞清楚啥是等倾干涉。

咱就说有一束平行光，它照到一个厚度均匀的薄膜上，比如就像那种薄薄的油膜。

这束光一部分会在薄膜的上表面反射，另一部分会穿过薄膜在下表面反射。

这两部分反射光要是相遇了，就可能产生干涉现象。

那啥是等倾干涉呢？就是说在这种干涉中，对于给定的入射光，具有相同倾角的光线会形成一组同心圆环的干涉条纹。

接下来咱们就说说求等倾干涉条纹的公式。

这就得提到光程差这个概念啦。

光程差可以用公式表示为：$\Delta L = 2nh\cos\theta$ 。

这里的$n$ 是薄膜的折射率，$h$ 是薄膜的厚度，$\theta$ 是入射光在薄膜表面的入射角。

当光程差是波长的整数倍时，就会出现亮条纹；当光程差是半波长的奇数倍时，就会出现暗条纹。

具体来说，亮条纹的条件是：$2nh\cos\theta = m\lambda$ ，其中$m$ 是整数；暗条纹的条件是：$2nh\cos\theta = (2m + 1)\frac{\lambda}{2}$ 。

我记得有一次给学生们讲这个知识点的时候，有个学生就特别迷糊，一直问我：“老师，这咋就干涉啦？”我就耐心地给他举例子。

我拿了两块玻璃片，中间夹了一点水，让一束光从侧面照过去，然后在白色的屏幕上真的就出现了一圈一圈的条纹。

我指着那些条纹跟他说：“你看，这就是等倾干涉产生的条纹，就像咱们刚刚讲的那样。

”这孩子眼睛一下子就亮了，好像突然就明白了。

咱们再回过头来看这个公式，在实际应用中，比如在研究薄膜的光学性质、测量薄膜的厚度等方面，这个公式都特别有用。

比如说，知道了薄膜的折射率和厚度，以及观察到的干涉条纹的情况，就可以通过这个公式来计算入射光的波长。

总之，等倾干涉条纹公式虽然看起来有点复杂，但只要咱们理解了它背后的物理原理，再结合实际的观察和实验，就能很好地掌握和运用它。

这样，在解决相关的光学问题时，就能更加得心应手啦！。

迈克尔逊等倾及等厚干涉图样前言：在大学物理实验中，使用的是传统迈克尔逊干涉仪，其常见的实验内容是：观察等倾干涉条纹，观察等厚干涉条纹，测量激光或钠光的波长，测量钠光的双线波长差，测量玻璃的厚度或折射率等。

本文用Mathematica软件数值模拟了迈克尔逊等倾及等厚干涉，并用Origin软件处理数据，得到了等倾及等厚干涉图样。

1. 迈克尔逊千涉仪中等倾等厚干涉条纹1.1迈克尔逊等倾干涉是薄膜干涉的一种。

薄膜此时是均匀的，光线以倾角i入射，上下两条反射光线经过透镜作用汇聚一起，形成干涉。

由于入射角相同的光经薄膜两表面反射形成的反射光在相遇点有相同的光程差，也就是说，凡入射角相同的就形成同一条纹，故这些倾斜度不同的光束经薄膜反射所形成的干涉花样是一些明暗相间的同心圆环.这种干涉称为等倾干涉。

倾角i相同时，干涉情况一样(因此叫做"等倾干涉")h一定时，干涉级数愈高(j愈大)，相当于i2愈小.此外，等倾干涉条纹只呈现在会聚平行光的透镜的焦平面上，不用透镜时产生的干涉条纹应在无限远处，所以我们说等倾干涉条纹定域于无限远处。

2.1.1光程差公式薄膜干涉中两相干光的光程差公式(表示为入射角的函数形式)为式中n为薄膜的折射率;n0为空气的折射率;h为入射点的薄膜厚度;i0为薄膜的入射角;+λ/2为由于两束相干光在性质不同的两个界面(一个是光疏-光密界面，另一是光密-光疏界面)上反射而引起的附加光程差;λ为真空中波长。

薄膜干涉原理广泛应用于光学表面的检验、微小的角度或线度2．1.1干涉图样当光程差为波长整数倍时，形成亮条纹，为半波长奇数倍时是暗条纹。

等倾条纹是内疏外密的同心圆环。

2.2迈克尔逊干涉仪等候干涉图样薄膜干涉分为两种一种叫等倾干涉，另一种称做等厚干涉。

等厚干涉是由平行光入射到厚度变化均匀、折射率均匀的薄膜上、下表面而形成的干涉条纹．薄膜厚度相同的地方形成同条干涉条纹，故称等厚干涉．牛顿环和楔形平板干涉都属等厚干涉．2.2.1基本原理当一束平行光ab入射到厚度不均匀的透明介质薄膜上，在薄膜的表面上会产生干涉现象。

物理教学内容研究案例--等倾干涉和等厚干涉的差别等倾干涉和等厚干涉是干涉现象的两种形式，它们之间有着一定的差别。

本文将分别介绍等倾干涉和等厚干涉的原理、特点、实验方法和应用，并对它们进行比较分析，以便更好地理解它们之间的差别。

首先，我们将介绍等倾干涉和等厚干涉的基本原理。

一、等倾干涉的原理等倾干涉是指两束光波以等角度入射到一块平行双面玻璃或石英玻璃板上，在受到反射后形成干涉条纹的现象。

在等倾干涉实验中，我们可以用一块平行双面玻璃或石英玻璃板将一束光波分为两束，再将这两束光波重新相遇在另一块相同的平行双面玻璃或石英玻璃板上，这时就会观察到明暗交替的干涉条纹。

这是因为在双面玻璃或石英玻璃板上，由于反射和折射的作用，光波在不同位置形成了不同相位的差异，进而产生了干涉现象。

二、等倾干涉的特点等倾干涉具有明显的特点，其中包括以下几点：1.干涉条纹清晰明确，呈现出直线或弧线的条纹模样；2.两个入射光线的夹角恒定，即角度相等或近似相等；3.干涉条件比较宽松，只要入射角度基本相等即可产生干涉现象。

三、等倾干涉的实验方法进行等倾干涉实验时，我们可以采用以下步骤进行：1.准备一块平行双面玻璃或石英玻璃板，通过光源将其照射；2.观察干涉现象，并记录下干涉条纹的分布情况和特点；3.在实验中，我们可以通过改变光源的位置、角度或波长等参数，来观察干涉条纹的变化。

四、等倾干涉的应用等倾干涉在实际应用中有着广泛的应用，其中包括：1.利用等倾干涉可以测量材料的折射率和薄膜厚度；2.可以利用等倾干涉进行光学元件的检测和校准；3.在天文学和地质学中，等倾干涉也被广泛应用于距离和形状的测量等方面。

接下来，我们将介绍等厚干涉的原理、特点、实验方法和应用。

五、等厚干涉的原理等厚干涉是指在两个相距较远的平行面上，由于膜厚的变化所产生的干涉现象。

当两个平行面之间有一薄膜时，在入射光线与薄膜表面发生反射和折射后，在两个平行面上形成了干涉条纹。

这一干涉现象即为等厚干涉。

物理教学内容研究案例--等倾干涉和等厚干涉的差别等倾干涉和等厚干涉是物理教学中常见的两种干涉现象。

它们之间的差别在于干涉产生的原理、特点以及应用方面都有所不同。

本文将详细探讨等倾干涉和等厚干涉的差别，从物理原理、实验现象以及实际应用三个方面进行详细分析。

一、物理原理等倾干涉是指两束相干光通过等倾薄膜或玻璃板后，在干涉图样中观察到的干涉现象。

等倾薄膜是指两片平行的玻璃板之间夹有一层薄膜，当两束光线通过薄膜后，由于薄膜两侧的折射率不同，光线会发生相位差，从而产生干涉现象。

而等厚干涉是指两束相干光通过等厚介质板，也就是两片平行的玻璃板之间没有夹膜的干涉现象。

当两束光线通过等厚介质板时，由于介质板的等厚性，光线在通过介质板后会发生相位差，从而产生干涉现象。

从物理原理上来看，等倾干涉是由于薄膜两侧折射率不同而导致的相位差，而等厚干涉则是由于介质板等厚性导致的相位差。

二、实验现象等倾干涉和等厚干涉在实验现象上也有明显的区别。

在等倾干涉实验中，我们可以观察到明暗条纹交替排列的干涉图样。

这是由于等倾薄膜两侧的折射率不同，导致通过薄膜的光线会发生相位差，从而在干涉图样中形成明暗条纹。

而在等厚干涉实验中，观察到的干涉图样往往是均匀亮暗交替的条纹。

这是由于等厚介质板的等厚性导致通过介质板的光线也会发生相位差，形成均匀的干涉条纹。

实验现象的不同也反映了等倾干涉和等厚干涉在物理性质上的差异。

三、实际应用等倾干涉和等厚干涉在实际应用中有着不同的用途。

等倾干涉常常用于薄膜的测厚和材料的质量检测中。

通过观察等倾干涉图样的明暗条纹，可以测定薄膜的厚度和材料的质量。

而等厚干涉则常常用于非球面透镜的制作和测量中。

由于等厚介质板会产生均匀的干涉条纹，因此可以用于非球面透镜的制作和检验。

在实际应用中，等倾干涉和等厚干涉都发挥着重要的作用，但其应用领域和方法有所不同。

综上所述，等倾干涉和等厚干涉在物理原理、实验现象和实际应用上都有着明显的差异。