下载文档原格式
等厚干涉实验报告等厚干涉实验报告引言：等厚干涉实验是一种基于干涉现象的光学实验，通过观察光的干涉现象来研究光的性质和行为。
在这个实验中，我们使用了一台干涉仪来观察等厚干涉现象，并对其进行了深入的研究和分析。
实验目的：通过等厚干涉实验，我们的目的是探究光的干涉现象，研究光的波动性质，并通过实验结果来验证干涉理论。
实验原理：等厚干涉实验基于的原理是光的干涉现象。
当两束光波相遇时，它们会发生干涉，产生干涉条纹。
在等厚干涉实验中，我们使用了一台干涉仪，它由一个透明的分波镜和两个平行的玻璃板组成。
当光通过分波镜后，被分成两束，分别经过两个平行的玻璃板。
当这两束光波再次相遇时，它们会产生干涉现象。
实验步骤：1. 准备工作：调整干涉仪的光源，使其发出单色光。
2. 调整干涉仪：通过调整干涉仪的分波镜和玻璃板的位置，使得两束光波相遇时形成清晰的干涉条纹。
3. 观察干涉条纹：使用目镜或显微镜观察干涉条纹的形状和颜色，并记录下观察结果。
4. 改变光源：尝试使用不同颜色的光源，观察干涉条纹的变化，并记录下观察结果。
5. 改变玻璃板的厚度：在实验过程中，逐渐改变玻璃板的厚度，观察干涉条纹的变化，并记录下观察结果。
实验结果：通过观察等厚干涉实验的结果，我们可以发现以下几个现象：1. 干涉条纹的形状：干涉条纹呈现出明暗相间的条纹，形状有时呈现出直线，有时呈现出弯曲的形状。
2. 干涉条纹的颜色：干涉条纹的颜色随着光源的改变而变化，不同颜色的光源会产生不同颜色的干涉条纹。
3. 玻璃板厚度的影响：改变玻璃板的厚度会导致干涉条纹的变化，厚度增加时，干涉条纹会变得更加密集。
实验分析：通过对等厚干涉实验的观察和分析，我们可以得出以下结论：1. 光的波动性质：干涉现象表明光具有波动性质，不同光波之间会发生干涉。
2. 光的波长：干涉条纹的间距和颜色的变化可以用来测量光的波长，从而进一步研究光的性质。
3. 玻璃板的厚度：玻璃板的厚度对干涉条纹的形状和密度有着显著的影响，通过改变玻璃板的厚度，我们可以调控干涉条纹的形态。
等厚干涉原理与应用实验报告篇一：等厚干涉实验—牛顿环和劈尖干涉等厚干涉实验—牛顿环和劈尖干涉要观察到光的干涉图象，如何获得相干光就成了重要的问题，利用普通光源获得相干光的方法是把由光源上同一点发的光设法分成两部分，然后再使这两部分叠如起来。
由于这两部分光的相应部分实际上都来自同一发光原子的同一次发光，所以它们将满足相干条件而成为相干光。
获得相干光方法有两种。
一种叫分波阵面法，另一种叫分振幅法。
1．实验目的（1）通过对等厚干涉图象观察和测量，加深对光的波动性的认识。
（2）掌握读数显微镜的基本调节和测量操作。
（3）掌握用牛顿环法测量透镜的曲率半径和用劈尖干涉法测量玻璃丝微小直径的实验方法（4）学习用图解法和逐差法处理数据。
2．实验仪器读数显微镜，牛顿环，钠光灯3．实验原理我们所讨论的等厚干涉就属于分振幅干涉现象。
分振幅干涉就是利用透明薄膜上下表面对入射光的反射、折射，将入射能量(也可说振幅)分成若干部分，然后相遇而产生干涉。
分振幅干涉分两类称等厚干涉，一类称等倾干涉。
用一束单色平行光照射透明薄膜，薄膜上表面反射光与下表面反射光来自于同一入射Rre(a)(b)图9-1 牛顿环装置和干涉图样光，满足相干条件。
当入射光入射角不变，薄膜厚度不同发生变化，那么不同厚度处可满足不同的干涉明暗条件，出现干涉明暗条纹，相同厚度处一定满足同样的干涉条件，因此同一干涉条纹下对应同样的薄膜厚度。
这种干涉称为等厚干涉，相应干涉条纹称为等厚干涉条纹。
等厚干涉现象在光学加工中有着广泛应用，牛顿环和劈尖干涉就属于等厚干涉。
下面分别讨论其原理及应用：（1）用牛顿环法测定透镜球面的曲率半径牛顿环装置是由一块曲率半径较大的平凸玻璃透镜和一块光学平玻璃片(又称“平晶”)相接触而组成的。
相互接触的透镜凸面与平玻璃片平面之间的空气间隙，构成一个空气薄膜间隙，空气膜的厚度从中心接触点到边缘逐渐增加。
如图9-1（a）所示。
当单色光垂直地照射于牛顿环装置时(如图9-1)，如果从反射光的方向观察，就可以看到透镜与平板玻璃接触处有一个暗点，周围环绕着一簇同心的明暗相间的内疏外密圆环，这些圆环就叫做牛顿环，如图9-1（b）所示．在平凸透镜和平板玻璃之间有一层很薄的空气层，通过透镜的单色光一部分在透镜和空气层的交界面上反射，一部分通过空气层在平板玻璃上表面上反射，这两部分反射光符合相干条件，它们在平面透镜的凸面上相遇时就会产生干涉现象。
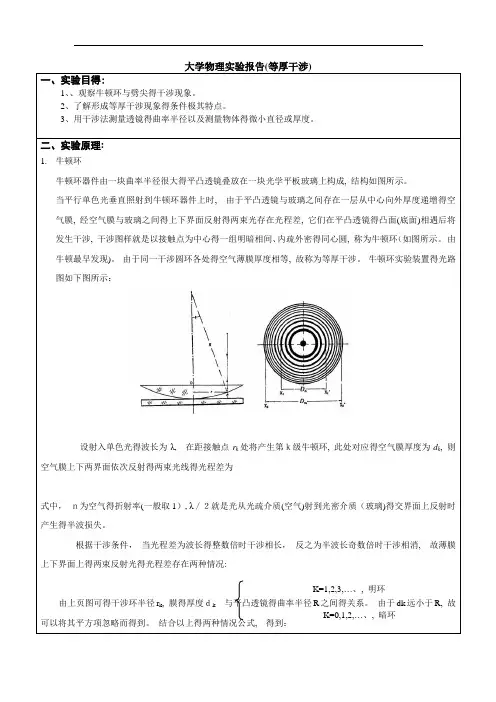
一、实验目得:1、、观察牛顿环与劈尖得干涉现象。
2、了解形成等厚干涉现象得条件极其特点。
3、用干涉法测量透镜得曲率半径以及测量物体得微小直径或厚度。
二、实验原理:1.牛顿环牛顿环器件由一块曲率半径很大得平凸透镜叠放在一块光学平板玻璃上构成, 结构如图所示。
当平行单色光垂直照射到牛顿环器件上时,由于平凸透镜与玻璃之间存在一层从中心向外厚度递增得空气膜, 经空气膜与玻璃之间得上下界面反射得两束光存在光程差, 它们在平凸透镜得凸面(底面)相遇后将发生干涉, 干涉图样就是以接触点为中心得一组明暗相间、内疏外密得同心圆, 称为牛顿环（如图所示。
由牛顿最早发现)。
由于同一干涉圆环各处得空气薄膜厚度相等, 故称为等厚干涉。
牛顿环实验装置得光路图如下图所示：设射入单色光得波长为λ,在距接触点r k处将产生第ｋ级牛顿环, 此处对应得空气膜厚度为d k, 则空气膜上下两界面依次反射得两束光线得光程差为式中，ｎ为空气得折射率(一般取1）, λ／２就是光从光疏介质(空气)射到光密介质（玻璃)得交界面上反射时产生得半波损失。
根据干涉条件，当光程差为波长得整数倍时干涉相长，反之为半波长奇数倍时干涉相消,故薄膜上下界面上得两束反射光得光程差存在两种情况:由上页图可得干涉环半径r k, 膜得厚度ｄk与平凸透镜得曲率半径R之间得关系。
由于dk远小于R, 故可以将其平方项忽略而得到。
结合以上得两种情况公式,得到：K=1,2,3,…、, 明环K=0,1,2,…、, 暗环,由以上公式课件, r k与d k成二次幂得关系,故牛顿环之间并不就是等距得, 且为了避免背光因素干扰, 一般选取暗环作为观测对象。
而在实际中由于压力形变等原因, 凸透镜与平板玻璃得接触不就是一个理想得点而就是一个圆面; 另外镜面沾染回程会导致环中心成为一个光斑, 这些都致使干涉环得级数与半径无法准确测量。
而使用差值法消去附加得光程差,用测量暗环得直径来代替半径,都可以减少以上类型得误差出现。
等厚干涉及其应用实验报告一、实验目的1. 了解等厚干涉的原理和方法。
2. 学习等厚干涉实验的基本技术及注意事项。
3. 掌握等厚干涉的应用。
二、实验仪器和材料1. 干涉仪2. 光源3. 透镜4. 反射镜5. 单色滤光片6. 微调平台7. 测量规等三、实验原理等厚干涉的原理是利用二分法来消除不均匀板材的厚度差异，使板材成为等厚的状况，然后通过干涉仪的干涉检查等厚度情况。
二分法的原理是使用两个不同波长的光源进行光程差测量，通过计算前后两次干涉的相位差，得到样品的厚度。
四、实验步骤1. 调整干涉仪的光源及其它必要的物件，使探测器接收到最强的光。
2. 将样品板安装在微调平台上，调整为初始位置，并将单色滤光片放在光源前方。
3. 调整反射镜使两束光重合并产生干涉条纹。
4. 通过干涉仪镜臂微调，调整测量表计读数。
5. 移动微调平台，使干涉条纹数量增加。
6. 测量板的厚度及其表面情况，记录实验数据。
五、实验结果及分析1. 在不同的干涉条件下，得到的干涉条纹间隔均匀，且随着板材的尺寸变化而变化。
2. 利用等厚干涉可测量厚度小于毫米级别的物体，且精度高、准确度高。
3. 根据所得数据，可计算出板材的等厚度，并结合其它参数进行分析。
六、实验结论本实验通过等厚干涉实验方法，得到了比较准确的板材等厚度测量结果，并且了解到等厚干涉的应用方向及其优点。
该实验方法线性精度高、稳定性效果佳，且可以测量一些薄板或其他一些难以测量的物体，治理误差准确度高，具有较大的应用价值。
七、实验心得在本次实验中，我们通过实际操作了解等厚干涉实验原理与方法，并根据测量数据对所得结果进行了分析和判断。
实验提供了一个有效的方法，可以在行业中用于硬度测量、材料分析等数据处理。
对于我而言，这次实验在技术和实践操作方面都起到了很好的学习和提升作用。
等厚干涉及其应用实验报告嘿，大家好！今天咱们聊聊等厚干，听起来是不是有点高大上，其实呢，它就是一种在材料科学里特别好用的小工具。
等厚干这东西，简单来说就是把材料做得均匀厚度，然后进行各种测试，看看它的性能到底咋样。
你说，这和咱们日常生活有什么关系呢？其实关系可大了！就像咱们吃的蛋糕，切得均匀了，才能每块都好吃嘛！如果你吃到一块特别厚的，那简直就是悲剧。
咱们的实验就是围绕这个“等厚”来展开的。
我们准备了一些样品，材料各不相同，有金属，有塑料，还有那些神秘的合金，简直是五花八门。
然后就开始了我们的大显身手。
为了确保厚度均匀，我们用上了各种仪器，测量得跟精细的厨师做蛋糕一样。
哎呀，那感觉真是紧张兮兮的，生怕一不小心就搞错了。
就像玩游戏打boss一样，稍微出错就得重来。
实验的过程中，我们有个小伙子，叫小明。
他特热衷于用一些生动的比喻来形容这些材料。
小明说，这金属就像个硬汉，强壮得不得了，而塑料就像个柔情似水的姑娘，虽然轻巧但很容易变形。
哈哈，大家都乐了，这比喻真形象！小明每次发言都能把大家逗笑，轻松的氛围让实验也变得更顺利了。
接下来的步骤就是对这些样品进行一系列的测试，看看它们的耐压、耐温和抗腐蚀能力。
我们一边测试，一边讨论，现场气氛那叫一个火热。
测试的时候，有个同学把样品弄掉了，砸到了桌子上，发出“咣当”的一声。
大家瞬间都停下来了，心想这下完了，材料肯定要报废。
结果一看，居然没事，真是个意外之喜，大家都松了一口气。
等我们把所有数据都收集齐后，开始分析结果。
这时候，才真是见证了团队的力量。
每个人都在各自的领域里发挥着作用，像一台高效的机器，转起来就停不下来。
我们用各种图表、公式把数据整合在一起，像拼图一样，慢慢拼出一个个有趣的发现。
最有意思的是，有些材料的表现出乎意料，真是让人大开眼界。
我们总结了一下这次实验的收获。
不仅学到了等厚干的应用，也意识到团队合作的重要性。
就像打麻将，四个人齐心协力，才能赢得漂亮。
等厚干涉原理与应用实验报告.doc 等厚干涉原理与应用实验报告一、实验目的1.理解和掌握等厚干涉原理及基本原理公式；2.学会使用等厚干涉仪器进行实验操作；3.观察等厚干涉现象，分析实验结果；4.应用等厚干涉原理解决实际问题。
二、实验原理等厚干涉是指两束或多束相干光波在一定条件下相遇，产生干涉现象。
其基本原理是当两束光波的相位差等于2π的整数倍时，它们叠加产生亮条纹；相位差为2π的奇数倍时，叠加产生暗条纹。
因此，等厚干涉通常被用于测量表面平整度、薄膜厚度、液体折射率等。
在等厚干涉实验中，通常使用钠灯发出的黄光作为光源，因其相干长度较大，可获得较明显的干涉条纹。
实验中需要将待测表面放置在空气薄膜的一侧，通过调节薄膜厚度，使两束光波在表面反射后产生相干，从而形成等厚干涉条纹。
三、实验步骤1.准备实验器材：钠灯、显微镜、光屏、载物台、测微目镜、尺子、待测表面（如平面玻璃）。
2.将钠灯放置在显微镜的聚光器下，调整显微镜和钠灯的距离，使光源通过显微镜后照射到待测表面上。
3.将待测表面放置在显微镜的载物台上，调整显微镜的焦距，使其清晰地观察到干涉条纹。
4.将光屏放置在显微镜的侧面，使其与显微镜的出射光路平齐，从而能够接收干涉条纹。
5.调节显微镜的焦距和光屏的角度，使干涉条纹清晰可见。
此时可通过观察测微目镜或尺子测量干涉条纹的间距。
6.根据测量的结果计算待测表面的平整度或薄膜厚度。
四、实验结果与分析1.在本次实验中，我们成功观察到了等厚干涉条纹。
通过调节显微镜和光屏的角度，使条纹清晰可见。
我们发现，当显微镜和光屏之间的距离增加时，条纹之间的间距变小；反之，间距变大。
这表明条纹间距与显微镜和光屏之间的距离成反比关系。
2.通过测量条纹间距，我们计算出了待测表面的平整度。
具体来说，我们首先计算了相邻亮条纹之间的距离d（单位为毫米），然后根据公式平整度=d/2n（n为折射率），计算出平整度（单位为毫米）。
结果表明，待测表面的平整度较高。
大物实验等厚干涉实验报告一、实验目的1、观察等厚干涉现象，加深对光的波动性的理解。
2、掌握用牛顿环测量平凸透镜曲率半径的方法。
3、学会使用读数显微镜。
二、实验原理1、等厚干涉当一束平行光垂直入射到厚度不均匀的透明薄膜上时，在薄膜的上、下表面反射的两束光将会产生干涉现象。
由于薄膜厚度不同，两束反射光的光程差也不同，在某些位置两束光相互加强，出现亮条纹；在另一些位置两束光相互削弱，出现暗条纹。
这种因薄膜厚度相同的地方形成相同干涉条纹的现象称为等厚干涉。
2、牛顿环将一块曲率半径较大的平凸透镜放在一块平面玻璃上，在透镜的凸面与玻璃之间形成一空气薄层。
当平行单色光垂直入射时，在空气薄层的上、下表面反射的两束光将产生干涉。
由于空气薄层的厚度从中心到边缘逐渐增加，所以在反射光中形成以接触点为中心的一系列明暗相间的同心圆环，称为牛顿环。
3、曲率半径的计算设透镜的曲率半径为＄R$，在空气薄膜厚度为＄e$ 处，两束反射光的光程差为＄＼Delta ＝ 2e ＋＼frac{＼lambda}｛2}＄，其中＄＼lambda$ 为入射光的波长。
当光程差为波长的整数倍时，出现亮条纹，即：＼2e ＋＼frac{＼lambda}｛2} ＝ k\lambda ＼quad （k ＝ 1, 2, 3, ＼cdots)＼当光程差为半波长的奇数倍时，出现暗条纹，即：＼2e ＋＼frac{＼lambda}｛2} ＝（2k ＋ 1)＼frac{＼lambda}｛2} ＼quad （k ＝ 0, 1, 2, 3, ＼cdots)＼在牛顿环中，中心处（＄k ＝ 0$）的干涉条纹是暗纹。
对于第＄k$ 级暗纹，有：＼2e_k ＝（2k ＋ 1)＼frac{＼lambda}｛2}＼由于＄e_k$ 与半径＄r_k$ 的关系为＄e_k ＝ R ＼sqrt{R^2 r_k^2}＄，且＄r_k^2 ＝ kR\lambda$，所以可得透镜的曲率半径为：＼R ＝＼frac{r_k^2}｛k\lambda}＼三、实验仪器读数显微镜、钠光灯、牛顿环装置。
一、实验目的1. 了解等厚干涉的原理和现象。
2. 掌握等厚干涉实验的原理和方法。
3. 学习使用干涉仪进行等厚干涉实验，并观察干涉条纹。
4. 了解等厚干涉在光学测量中的应用。
二、实验原理等厚干涉是指两束相干光在厚度不同的介质中传播时，由于光程差的不同，导致干涉条纹的分布规律。
在等厚干涉实验中，通过调节干涉仪的装置，使两束相干光在薄膜上产生干涉，观察干涉条纹的分布情况。
等厚干涉实验的原理如下：1. 当一束单色光垂直照射到厚度不均匀的薄膜上时，光在薄膜的上下表面反射，形成两束相干光。
2. 由于薄膜的厚度不均匀，两束光的光程差也随之变化，从而产生干涉现象。
3. 当光程差为整数倍波长时，干涉条纹为亮条纹；当光程差为半整数倍波长时，干涉条纹为暗条纹。
三、实验仪器与材料1. 干涉仪2. 干涉片3. 准直器4. 单色光源5. 平面镜6. 秒表四、实验内容1. 安装干涉仪，调整光源、准直器和平面镜，使光束垂直照射到干涉片上。
2. 观察干涉条纹的分布情况，记录干涉条纹的形状、间距和颜色。
3. 通过改变干涉片的厚度，观察干涉条纹的变化，分析等厚干涉现象。
4. 使用干涉仪测量干涉条纹的间距，计算薄膜的厚度。
五、实验步骤1. 安装干涉仪，调整光源、准直器和平面镜，使光束垂直照射到干涉片上。
2. 观察干涉条纹的分布情况，记录干涉条纹的形状、间距和颜色。
3. 调节干涉仪的装置，使干涉片在垂直方向上移动，观察干涉条纹的变化。
4. 记录干涉条纹的间距，使用干涉仪测量干涉条纹的间距。
5. 根据干涉条纹的间距和光程差的关系，计算薄膜的厚度。
六、实验结果与分析1. 通过观察干涉条纹的分布情况，可以观察到干涉条纹的形状、间距和颜色。
在干涉条纹中，亮条纹和暗条纹的分布规律与薄膜的厚度有关。
2. 通过改变干涉片的厚度，可以观察到干涉条纹的变化。
当干涉片的厚度增加时，干涉条纹的间距减小；当干涉片的厚度减小时，干涉条纹的间距增大。
3. 通过测量干涉条纹的间距，可以计算出薄膜的厚度。
大物等厚干涉实验报告一、实验目的1、观察等厚干涉现象，加深对光的波动性的理解。
2、掌握用牛顿环测量平凸透镜曲率半径的方法。
3、学会使用读数显微镜。
二、实验原理1、等厚干涉当一束平行光垂直照射到厚度不均匀的透明薄膜上时，在薄膜表面会产生干涉现象。
这种干涉条纹是由同一厚度处的反射光相干叠加形成的，因此称为等厚干涉。
2、牛顿环将一块曲率半径较大的平凸透镜放在一块平面玻璃上，在两者之间形成一空气薄层。
当单色光垂直入射时，在透镜表面会形成一组以接触点为中心的明暗相间的同心圆环，称为牛顿环。
设平凸透镜的曲率半径为 R，入射光波长为λ，在第 k 级暗环处，空气薄膜的厚度为 dk，则有：＼d_k ＝＼frac{k ＼lambda}｛2}＼由于 dk 远小于 R，所以可以近似认为 dk 等于第 k 级暗环半径 rk 的平方除以 2R，即：＼d_k ＝＼frac{r_k^2}｛2R}＼联立可得：＼r_k^2 ＝ kR\lambda＼通过测量第 k 级暗环的半径 rk，就可以计算出平凸透镜的曲率半径R。
三、实验仪器1、读数显微镜2、钠光灯3、牛顿环装置四、实验步骤1、调节读数显微镜（1）将显微镜镜筒大致调至水平。
（2）调节目镜，使十字叉丝清晰。
（3）将牛顿环装置放在显微镜载物台上，调节物镜，直至看清牛顿环。
2、测量牛顿环直径（1）转动测微鼓轮，使十字叉丝从牛顿环中心向左移动，依次测量第 15 到第 5 级暗环的位置，并记录数据。
（2）继续转动测微鼓轮，使十字叉丝越过中心向右移动，测量第 5 到第 15 级暗环的位置，并记录数据。
3、数据处理（1）计算各级暗环的直径。
（2）利用逐差法处理数据，计算平凸透镜的曲率半径 R 及其不确定度。
五、实验数据记录｜暗环级数｜左侧位置（mm）｜右侧位置（mm）｜直径（mm）｜｜｜｜｜｜｜ 15 ｜＿____ ｜＿____ ｜＿____ ｜｜ 14 ｜＿____ ｜＿____ ｜＿____ ｜｜ 13 ｜＿____ ｜＿____ ｜＿____ ｜｜ 12 ｜＿____ ｜＿____ ｜＿____ ｜｜ 11 ｜＿____ ｜＿____ ｜＿____ ｜｜ 10 ｜＿____ ｜＿____ ｜＿____ ｜｜ 9 ｜＿____ ｜＿____ ｜＿____ ｜｜ 8 ｜＿____ ｜＿____ ｜＿____ ｜｜ 7 ｜＿____ ｜＿____ ｜＿____ ｜｜ 6 ｜＿____ ｜＿____ ｜＿____ ｜｜ 5 ｜＿____ ｜＿____ ｜＿____ ｜六、数据处理1、计算各级暗环的直径：＼D_k ＝｜右侧位置左侧位置｜＼2、采用逐差法计算：＼＼Delta D ＝（D_{15} ＋ D_{11} ＋ D_{7} ＋ D_{3}）（D_{14} ＋ D_{10} ＋ D_{6} ＋ D_{2}）＼＼R ＝＼frac{（＼Delta D)＾2}｛4(10\lambda)｝＼3、计算不确定度：（1）测量暗环位置的不确定度：＼＼Delta x ＝＼Delta ＼text{仪器} ＝ 0005 ＼text{mm}＼＼＼Delta D_k ＝＼sqrt{2}＼Delta x＼（2）计算 R 的不确定度：＼＼Delta R ＝＼frac{＼Delta D}｛4(10\lambda)｝＼sqrt{＼left(＼frac{＼Delta D}｛D}＼right)＾2 ＋＼left(＼frac{＼Delta ＼lambda}｛＼lambda}＼right)＾2}＼七、实验结果与讨论1、实验结果计算得到平凸透镜的曲率半径 R ＝＿____ ±＿____ mm。
