统计学第五版第十四章统计指数
- 格式:docx
- 大小:47.91 KB
- 文档页数:7

第14章 指 数一、单项选择题1.考察总体中个别现象或个别项目数量变动的相对数称为( )。
A.个体指数B.总指数C.简单指数D.加权指数【答案】A【解析】个体指数是考察总体中个别现象或个别项目数量变动的相对数,如某种产品的产量指数、某种商品的价格指数等。
个体指数是计算总指数的基础。
2.反映数量指标变动程度的相对数称为( )。
A.数量指标指数B.质量指标指数C.简单指数D.加权指数【答案】A【解析】数量指标指数是反映数量指标变动程度的相对数,如商品销售量指数、工业产品产量指数等,数量指标通常采用实物计量单位。
3.综合反映多种项目数量变动的相对数称为( )。
A.数量指数B.质量指数C.个体指数D.总指数【答案】D【解析】总指数是综合反映多种项目数量变动的相对数,如多种产品的产量指数、多种商品的价格指数等。
4.拉氏指数方法是指在编制综合指数时( )。
A.用基期的变量值加权B.用报告期的变量值加权C.用固定某一时期的变量值加权D.选择有代表性时期的变量值加权【答案】A【解析】拉氏指数是1864年德国学者Laspeyres提出的一种价格指数计算方法,它在计算综合指数时将作为权数的同度量因素固定在基期。
5.帕氏指数方法是指在编制综合指数时( )。
A.用基期的变量值加权B.用报告期的变量值加权C.用固定某一时期的变量值加权D.选择有代表性时期的变量值加权【答案】B【解析】帕氏指数是1874年德国学者Paasche 提出的一种指数计算方法,它在计算综合指数时将作为权数的同度量因素固定在报告期。
6.拉氏指数的特点是( )。
A .权数固定在基期,不同时期的指数可以比较B .权数固定在基期,不同时期的指数不能比较C .权数固定在报告期,不同时期的指数可以比较D .权数固定在报告期,不同时期的指数不能比较【答案】A【解析】拉氏指数的特点是以基期变量值为权数,可以消除权数变动对指数的影响,从而使不同时期的指数具有可比性。

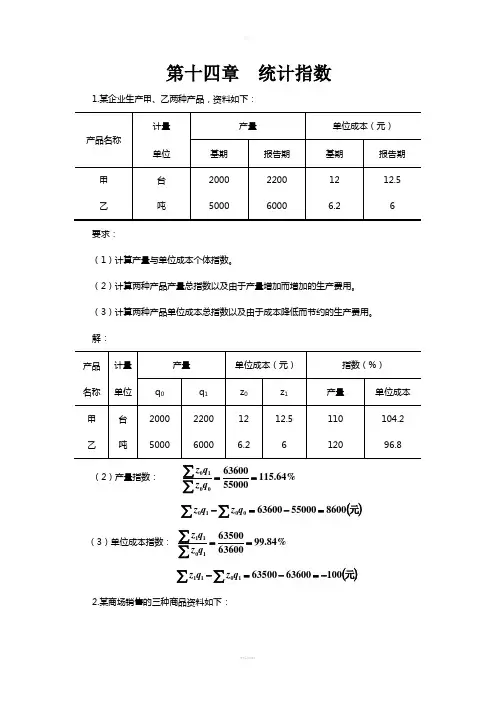
第十四章 统计指数1.某企业生产甲、乙两种产品,资料如下:要求:(1)计算产量与单位成本个体指数。
(2)计算两种产品产量总指数以及由于产量增加而增加的生产费用。
(3)计算两种产品单位成本总指数以及由于成本降低而节约的生产费用。
解:(2)产量指数:%64.1155500063600010==∑∑qz q z()∑∑=-=-元860055000636000010qz q z(3)单位成本指数:%84.9963600635001011==∑∑qz q z()∑∑-=-=-元10063600635001011qz q z2.某商场销售的三种商品资料如下: 要求:(1)计算三种商品的销售额总指数。
(2)分析销售量和价格变动对销售额影响的绝对值和相对值。
解:(1)销售额总指数:%06.1212600031475011==∑∑qp q p()∑∑=-=-元547526*********011qp q p(2)价格的变动:%29.10928800314751011==∑∑qp q p()∑∑=-=-元267528800314751011qp q p销售量的变动:%77.1102600028800010==∑∑qp q p()∑∑=-=-元280026000288000010qp q p3.试根据下列资料分别用拉氏指数和帕氏指数计算销售量指数及价格指数。
解:价格指数: %5.924804441011==∑∑qp q p %765003800001==∑∑q p q p销售量指数 %965004800010==∑∑qp qp %8.1163804440111==∑∑q p q p4.某公司三种产品的有关资料如下表,试问三种产品产量平均增长了多少,产量增长对产值有什么影响?解:%125260325601001006050.110010.110025.10000010001==++⨯+⨯+⨯===∑∑∑∑p q p q q q p q p q k q()∑∑=-=-万元652603250010qp q p三种产品产量平均增长了25%,由于产量增长使得产值也相应增长了25%,绝对额增加65万元。


第十四章 统计指数1.某企业生产甲、乙两种产品,资料如下:要求:(1)计算产量与单位成本个体指数。
(2)计算两种产品产量总指数以及由于产量增加而增加的生产费用。
(3)计算两种产品单位成本总指数以及由于成本降低而节约的生产费用。
解:(2)产量指数:%64.1155500063600010==∑∑qz q z()∑∑=-=-元860055000636000010qz q z(3)单位成本指数:%84.9963600635001011==∑∑qz q z()∑∑-=-=-元10063600635001011qz q z2.某商场销售的三种商品资料如下:要求:(1)计算三种商品的销售额总指数。
(2)分析销售量和价格变动对销售额影响的绝对值和相对值。
解: (1)销售额总指数:%06.1212600031475011==∑∑q p q p()∑∑=-=-元547526*********011qp q p(2)价格的变动:%29.10928800314751011==∑∑qp q p()∑∑=-=-元267528800314751011qp q p销售量的变动:%77.1102600028800010==∑∑qp q p()∑∑=-=-元280026000288000010qp q p3.试根据下列资料分别用拉氏指数和帕氏指数计算销售量指数及价格指数。
解: 价格指数:%5.924804441011==∑∑qp q p%76500380001==∑∑qp q p 销售量指数%965004800010==∑∑qp q p %8.116380444111==∑∑qp q p 4.某公司三种产品的有关资料如下表,试问三种产品产量平均增长了多少,产量增长对产值有什么影响?解:%125260325601001006050.110010.110025.10000010001==++⨯+⨯+⨯===∑∑∑∑p q pq q q p q p q k q ()∑∑=-=-万元652603250010qp q p三种产品产量平均增长了25%,由于产量增长使得产值也相应增长了25%,绝对额增加65万元。

STATISTICS (第三版第三版)作者:张占贞青岛科技大学经济与管理学院作者:张占贞青岛科技大学经济与管理学院STATISTICS (第三版第三版)作者:张占贞青岛科技大学经济与管理学院作者:张占贞青岛科技大学经济与管理学院STATISTICS (第三版第三版)作者:张占贞青岛科技大学经济与管理学院作者:张占贞青岛科技大学经济与管理学院2.3.4.STATISTICS (第三版第三版)作者:张占贞青岛科技大学经济与管理学院作者:张占贞青岛科技大学经济与管理学院§14.1加权指数14.1.1 加权综合指数14.1.2 加权平均指数统计学STATISTICS (第三版第三版)作者:张占贞青岛科技大学经济与管理学院作者:张占贞青岛科技大学经济与管理学院(index number )1.2.3.多个项目综合变动4.狭义的指数STATISTICS (第三版第三版)作者:张占贞青岛科技大学经济与管理学院作者:张占贞青岛科技大学经济与管理学院STATISTICS (第三版第三版)作者:张占贞青岛科技大学经济与管理学院作者:张占贞青岛科技大学经济与管理学院(weighted aggregative index number)1.加权2.3.STATISTICS (第三版第三版)作者:张占贞青岛科技大学经济与管理学院作者:张占贞青岛科技大学经济与管理学院(Laspeyres index)固定在基期∑STATISTICS (第三版第三版)作者:张占贞青岛科技大学经济与管理学院作者:张占贞青岛科技大学经济与管理学院(Paasche index)报告期∑统计学作者:张占贞青岛科技大学经济与管理学院作者:张占贞青岛科技大学经济与管理学院16002001501500150120统计学STATISTICS(第三版第三版)作者:张占贞青岛科技大学经济与管理学院作者:张占贞青岛科技大学经济与管理学院(例题分析)STATISTICS(第三版第三版)作者:张占贞青岛科技大学经济与管理学院作者:张占贞青岛科技大学经济与管理学院(例题分析)结论∶平均上涨STATISTICS(第三版第三版)作者:张占贞青岛科技大学经济与管理学院作者:张占贞青岛科技大学经济与管理学院(例题分析)结论∶平均上涨统计学STATISTICS(第三版第三版)作者:张占贞青岛科技大学经济与管理学院作者:张占贞青岛科技大学经济与管理学院(比较)可以消除销售量变动对价格指数的影响不能反映出消费结构的变化不能消除权数变动对价格指数的影响但帕氏指数可以同时反映出价格和消费结构的变化,具有比较明确的经济意义,因此,在实际应用中,常采用帕氏公式统计学STATISTICS(第三版第三版)作者:张占贞青岛科技大学经济与管理学院作者:张占贞青岛科技大学经济与管理学院统计学STATISTICS(第三版第三版)作者:张占贞青岛科技大学经济与管理学院作者:张占贞青岛科技大学经济与管理学院(weighted average index number)销售额为权数p 0q 0p 1q 11统计学作者:张占贞青岛科技大学经济与管理学院作者:张占贞青岛科技大学经济与管理学院1.201.051.14STATISTICS(第三版第三版)作者:张占贞青岛科技大学经济与管理学院作者:张占贞青岛科技大学经济与管理学院(例题分析)结论∶种产品的价格平均STATISTICS(第三版第三版)作者:张占贞青岛科技大学经济与管理学院作者:张占贞青岛科技大学经济与管理学院(例题分析)结论∶种产品的价格平均统计学STATISTICS(第三版第三版)作者:张占贞青岛科技大学经济与管理学院作者:张占贞青岛科技大学经济与管理学院§14.2几种常用的价格指数14.2.1 零售价格指数14.2.2 消费价格指数14.2.3 股票价格指数STATISTICS (第三版第三版)作者:张占贞青岛科技大学经济与管理学院作者:张占贞青岛科技大学经济与管理学院(retail price index)1.2.3.4.分层抽样在全国选择不同经济区域和分布合理的地区、以及有代表性的商品作为样本,对市场价格进行经常性目前,国家级抽选出的调查市、县226个STATISTICS (第三版第三版)作者:张占贞青岛科技大学经济与管理学院作者:张占贞青岛科技大学经济与管理学院(编制过程)经济区域和地区分布合理大、中、小城市和县调查地区包括集调查点STATISTICS (第三版第三版)作者:张占贞青岛科技大学经济与管理学院作者:张占贞青岛科技大学经济与管理学院(编制过程)消费量大、价格变动有代表性市场供应保持稳所选的代表STATISTICS (第三版第三版)作者:张占贞青岛科技大学经济与管理学院作者:张占贞青岛科技大学经济与管理学院(编制过程)派员直接社会商品零售额STATISTICS (第三版第三版)作者:张占贞青岛科技大学经济与管理学院作者:张占贞青岛科技大学经济与管理学院(consumer price index)1.2.3.编制过程与零售价格指数类似,不同的是它包括消费品价格和服务项目价格权数的确定STATISTICS (第三版第三版)作者:张占贞青岛科技大学经济与管理学院作者:张占贞青岛科技大学经济与管理学院(作用)统计学作者:张占贞青岛科技大学经济与管理学院作者:张占贞青岛科技大学经济与管理学院序列和居进统计学作者:张占贞青岛科技大学经济与管理学院作者:张占贞青岛科技大学经济与管理学院02000040000600008000010000012000014000016000019119219319419519619719819920020120220304年份国内生产总值国内生产总值(GDP)缩减后的GDPSTATISTICS (第三版第三版)作者:张占贞青岛科技大学经济与管理学院作者:张占贞青岛科技大学经济与管理学院(stock price index)1.2.(point )3.发行量为权数进行加权综合。
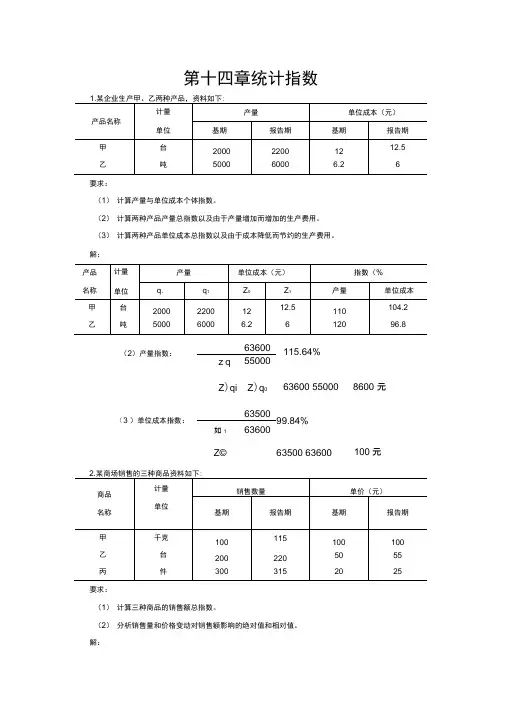
第十四章统计指数要求:(1)计算产量与单位成本个体指数。
(2)计算两种产品产量总指数以及由于产量增加而增加的生产费用。
(3)计算两种产品单位成本总指数以及由于成本降低而节约的生产费用。
解:(2)产量指数:63600 115.64%z°q°55000Z)qi Z)q0 63600 55000 8600 元(3 )单位成本指数:6350099.84% 如1 63600Z© 63500 63600 100元要求:(1)计算三种商品的销售额总指数。
(2)分析销售量和价格变动对销售额影响的绝对值和相对值。
解:(1)销售额总指数:P21 31475 121.06%P °q ° 26000Piq P °q ° 31475 260005475 元(2)价格的变动:pq 31475 109.29%P °q 128800Piqip °q i 31475 28800 2675 元销售量的变动:28800110.77%P °q °26000P 0q iP o q 。
28800 260002800 元3.试根据下列资料分别用拉氏指数和帕氏指数计算销售量指数及价格指数。
价格指数:一迪 444 —Piq0 鰹 P o q i 480P o q o 5004.某公司三种产品的有关资料如下表, 试问三种产品产量平均增长了多少, 产量增长对产值有什么影响?P 0q 1 P 0q 0 325 260 65万元三种产品产量平均增长了 25%由于产量增长使得产值也相应增长了25%绝对额增加65万元。
5. 三种商品销售资料如下,通过计算说明其价格总的变动情况。
q i销售量指数Po5 480 P o q o 50096%pg 444P i q o 380116.8%q 。
P 0q i P 0q 01.25 100 1.10 100 1.50 60 325q- -125%迪P °q 11 pqk p8634 144 26487 78%86 34 144 300. 760.90. 950. 8512.22%,绝对额减少 36.76万元。

统计学原理——统计指数统计指数是一项重要的统计学原理,它用于评估和比较不同群体或变量之间的相对差异。
通过统计指数,我们可以对数据进行更深入的分析,了解不同群体的差异以及其对总体的贡献。
在统计学中,常用的统计指数有多种,其中包括平均数、标准差、相关系数、协方差等。
这些指数可以帮助我们从不同角度对数据进行分析和解释。
首先,平均数是最常见的统计指数之一、它用于衡量一组数据的集中趋势和中心位置。
平均数可以通过将所有数据值相加并除以数据的个数来计算得到。
通过计算平均数,我们可以了解数据的总体特征和整体水平。
其次,标准差是用于衡量数据的离散程度和波动性的指数。
它衡量数据的每个数据点与平均数之间的距离,并计算这些距离的平均值。
标准差越大,表示数据的分布越分散;标准差越小,表示数据的分布越集中。
另外,相关系数是用于衡量两个变量之间相关性的指数。
它可以告诉我们两个变量之间的线性相关程度,取值范围从-1到1、当相关系数为正时,表示两个变量之间存在正相关关系;当相关系数为负时,表示两个变量之间存在负相关关系;当相关系数接近于0时,表示两个变量之间几乎没有相关性。
此外,协方差是用于衡量两个变量之间总体变化趋势的指数。
它可以告诉我们两个变量之间的总体变化方向和程度。
当协方差为正时,表示两个变量之间存在正相关关系;当协方差为负时,表示两个变量之间存在负相关关系;当协方差接近于0时,表示两个变量之间几乎没有线性关系。
这些统计指数对于统计学原理的应用非常重要。
通过计算和分析这些指数,我们可以从不同的角度深入了解数据的特征和关系,从而更好地进行数据的解释和应用。
在实际应用中,统计指数可以帮助我们研究不同群体之间的差异,并为决策提供依据。
例如,我们可以使用平均数和标准差来比较两个地区的人均收入水平和收入分布情况;我们可以使用相关系数和协方差来研究两个变量之间的相关性,如广告投资和销售额之间的关系。
总之,统计指数是统计学原理中重要的一部分,它可以帮助我们对数据进行更深入的分析和解释。


《统计学》补充作业第十四章补充作业1.考察总体中个别现象或个别项目数量变动的相对数称为()。
A.个体指数 B.总指数C.简单指数D加权指数2.反映数量指标变动程度的相对数称为()A.数量指标指数 B.质量指标指数C.简单指数D加权指数3.综合反映多种项目数量变动的相对数称为()A、数量指数B、质量指数C、个体指数D、总指数4.拉氏指数方法是指在编制综合指数时()A用基期的变量值加权 B用报告期的变量值加权C用固定某一时期的变量值加权 D选择有代表性时期的变量值加权5.帕氏指数方法是指在编制综合指数时()A用基期的变量值加权 B用报告期的变量值加权C用固定某一时期的变量值加权 D选择有代表性时期的变量值加权6.拉氏指数的特点是( )A .权数固定在基期,不同时期的指数可以比较。
B .权数固定在基期,不同时期的指数不能比较。
C .权数固定在报告期,不同时期的指数可以比较。
D .权数固定在报告期,不同时期的指数不能比较7.设p 为商品价格,q 为销售量,则指数∑∑010q p q p 的实际意义是综合反映( )。
A .商品销售额的变动程度B .商品价格变动对销售额的影响程度C .商品销售量变动对销售额的影响程度D .商品价格和销售量变动对销售额的影响程度8.使用基期价格作权数计算的商品销售量指数( ) A .包含了价格变动的影响 B .包含了价格和销售量变动的影响 C .消除了价格变动的影响 D .消除了价格和销售量变动的影响9.下列指数公式中哪个是拉氏数量指数公式( )A.∑∑0111q p q p B. ∑∑0001q p q p C. ∑∑0010q p q p D. ∑∑0011q p q p10.下列指数公式中哪个是帕氏价格指数公式( )A. ∑∑0011q p q p B. ∑∑1011q p q p C. ∑∑0001q p q p D. ∑∑0111q p q p11.在由三个指数构成的综合指数体系中,两个因素指数中的权数必须固定在()A. 报告期B. 基期C. 同一时期D. 不同时期12.由两个不同时期的总量对比形成的指数称为( ) A.总量指数 B.综合指数 C.加权综合指数 D.加权平均指数13.在指数体系中,总量指数与各因素指数之间的数量关系是( ) A.总量指数等于各因素指数之和 B.总量指数等于各因素指数之差 C.总量指数等于各因素指数之积 D.总量指数等于各因素指数之商14.某商店商品销售资料如下:表中所缺数值()A.105和125B.95和85C.85和80D.95和8015.某百货公司今年同去年相比,所有商品的价格平均提高了10%,销售量平均下降了10%,则商品销售额()A.上升B.下降C.保持不变D.可能上升也可能下降16.某地区2005的零售价格指数为105%,这说明()A.商品销售量增长了5%B.商品销售价格增长了5%C.由于价格变动使销售量增长了5%D.由于销售量变动使价格增长了5%17.某商场今年与去年相比,销售量增长了15%,价格增长了10%,则销售额增长了()A 4.8%B 26.5%C 1.5%D 4.5%18.某商店2005年与2006年相比,商品销售额增长了16%, 销售量增长了18%, 则销售价格增减变动的百分比为( )。

第十四章 统计指数1.某企业生产甲、乙两种产品,资料如下:要求:(1)计算产量与单位成本个体指数。
(2)计算两种产品产量总指数以及由于产量增加而增加的生产费用。
(3)计算两种产品单位成本总指数以及由于成本降低而节约的生产费用。
解:(2)产量指数:%64.1155500063600010==∑∑qz q z()∑∑=-=-元860055000636000010qz q z(3)单位成本指数:%84.9963600635001011==∑∑qz q z()∑∑-=-=-元10063600635001011qz q z2.某商场销售的三种商品资料如下: 要求:(1)计算三种商品的销售额总指数。
(2)分析销售量和价格变动对销售额影响的绝对值和相对值。
解:(1)销售额总指数:%06.1212600031475011==∑∑qp q p()∑∑=-=-元547526*********011qp q p(2)价格的变动:%29.10928800314751011==∑∑qp q p()∑∑=-=-元267528800314751011qp q p销售量的变动:%77.1102600028800010==∑∑qp q p()∑∑=-=-元280026000288000010qp q p3.试根据下列资料分别用拉氏指数和帕氏指数计算销售量指数及价格指数。
解: 价格指数:%5.924804441011==∑∑qp q p %765003800001==∑∑q p q p销售量指数%965004800010==∑∑qp q p %8.1163804440111==∑∑q p q p4.某公司三种产品的有关资料如下表,试问三种产品产量平均增长了多少,产量增长对产值有什么影响?解:%125260325601001006050.110010.110025.10000010001==++⨯+⨯+⨯===∑∑∑∑p q p q q q p q p q k q()∑∑=-=-万元652603250010qp q p三种产品产量平均增长了25%,由于产量增长使得产值也相应增长了25%,绝对额增加65万元。
应用统计学教案-统计指数第一章:统计指数概述1.1 指数的概念与分类1.1.1 复习指数的概念1.1.2 区分算术指数与几何指数1.1.3 引出统计指数的概念1.2 统计指数的性质与作用1.2.1 阐述统计指数的基本性质1.2.2 解释统计指数在经济学、社会学科等领域的应用1.2.3 强调统计指数在数据分析与决策中的重要性1.3 统计指数的编制方法1.3.1 介绍拉氏指数与帕氏指数的编制方法1.3.2 分析两种指数的优缺点及其适用场景1.3.3 演示编制简单统计指数的实例第二章:个体指数与综合指数2.1 个体指数的概念与计算2.1.1 引出个体指数的概念2.1.2 讲解个体指数的计算方法2.1.3 举例说明个体指数在实际应用中的作用2.2 综合指数的概念与计算2.2.1 介绍综合指数的概念2.2.2 阐述综合指数的计算方法2.2.3 分析综合指数在分析现象总体变动中的作用2.3 指数体系与同度量因素2.3.1 讲解指数体系的概念与构成2.3.2 阐释同度量因素的作用与选择原则2.3.3 举例说明同度量因素在实际应用中的重要性第三章:统计指数的计算与应用3.1 平均数指数的计算3.1.1 引出平均数指数的概念3.1.2 讲解平均数指数的计算方法3.1.3 演示计算平均数指数的实例3.2 链式指数的计算与应用3.2.1 介绍链式指数的概念与计算方法3.2.2 阐述链式指数在分析现象长期变动中的作用3.2.3 举例说明链式指数在实际应用中的重要性3.3 统计指数在实际应用中的案例分析3.3.1 分析消费者价格指数(CPI)的计算与作用3.3.2 讲解生产者价格指数(PPI)的计算与作用3.3.3 探讨统计指数在其他领域的应用实例第四章:统计指数的分析与评价4.1 统计指数分析的方法与技巧4.1.1 引出统计指数分析的方法与技巧4.1.2 讲解比较分析、因素分析等方法在统计指数分析中的应用4.1.3 演示统计指数分析的实例4.2 统计指数评价的标准与原则4.2.1 阐述统计指数评价的标准与原则4.2.2 分析评价标准与原则在实际应用中的重要性4.2.3 讨论评价标准与原则的局限性与改进方向4.3 统计指数在政策制定与决策中的应用4.3.1 讲解统计指数在政策制定与决策中的作用4.3.2 分析统计指数在国民经济核算、价格调控等领域的应用实例4.3.3 探讨统计指数在决策过程中的优化与改进第五章:统计指数的拓展与应用5.1 统计指数与经济预测5.1.1 引出统计指数在经济预测中的应用5.1.2 讲解经济预测方法与统计指数的结合5.1.3 演示统计指数在经济预测中的实例5.2 统计指数与大数据分析5.2.1 介绍大数据时代统计指数的新发展5.2.2 阐述大数据分析技术与统计指数的结合5.2.3 探讨大数据时代统计指数在决策支持中的作用与挑战5.3 统计指数在其他领域的应用5.3.1 分析统计指数在社会科学、环境科学等领域的应用实例5.3.2 讲解统计指数在其他领域的拓展与应用5.3.3 展望统计指数在未来发展中的前景与挑战第六章:指数平滑法在统计指数中的应用6.1 指数平滑法的基本原理6.1.1 引出指数平滑法6.1.2 讲解指数平滑法的基本原理6.1.3 演示计算指数平滑法的实例6.2 指数平滑法在统计指数中的应用6.2.1 介绍指数平滑法在统计指数中的应用6.2.2 阐述指数平滑法在时间序列预测中的优势6.2.3 举例说明指数平滑法在实际应用中的重要性6.3 指数平滑法的拓展与改进6.3.1 讲解指数平滑法的拓展与改进6.3.2 分析拓展与改进在提高预测精度中的作用6.3.3 探讨指数平滑法在实际应用中的局限性与改进方向第七章:多元统计指数分析7.1 多元统计指数的概念与分类7.1.1 引出多元统计指数的概念7.1.2 区分不同类型的多元统计指数7.1.3 阐述多元统计指数在分析多因素变动中的作用7.2 多元统计指数的计算方法7.2.1 讲解多元统计指数的计算方法7.2.2 分析各种计算方法的优缺点及其适用场景7.2.3 演示计算多元统计指数的实例7.3 多元统计指数在实际应用中的案例分析7.3.1 分析多元统计指数在市场分析、产品质量评价等领域的应用实例7.3.2 讲解多元统计指数在实际应用中的重要性7.3.3 探讨多元统计指数在解决实际问题中的局限性与改进方向第八章:统计指数与国民经济核算8.1 国民经济核算体系与统计指数8.1.1 引出国民经济核算体系与统计指数的关系8.1.2 讲解国民经济核算体系的基本概念与方法8.1.3 阐述统计指数在国民经济核算中的应用8.2 国内生产总值(GDP)的统计指数分析8.2.1 介绍国内生产总值(GDP)的概念与计算方法8.2.2 分析统计指数在GDP计算与分析中的应用8.2.3 举例说明统计指数在GDP分析中的重要性8.3 国民经济其他指标的统计指数分析8.3.1 分析消费价格指数(CPI)、生产价格指数(PPI)等指标的统计指数应用8.3.2 讲解统计指数在其他国民经济指标分析中的应用实例8.3.3 探讨统计指数在国民经济分析中的局限性与改进方向第九章:统计指数在金融领域的应用9.1 统计指数在金融市场分析中的应用9.1.1 引出统计指数在金融市场分析中的应用9.1.2 讲解金融市场指数的编制与分析方法9.1.3 阐述统计指数在金融市场分析中的重要性9.2 统计指数在金融风险管理中的应用9.2.1 介绍统计指数在金融风险管理中的应用9.2.2 分析统计指数在风险评估、预警等方面的作用9.2.3 举例说明统计指数在金融风险管理中的重要性9.3 统计指数在其他金融领域的应用9.3.1 分析统计指数在信用评级、资产定价等领域的应用实例9.3.2 讲解统计指数在其他金融领域的应用与价值9.3.3 探讨统计指数在金融领域发展的局限性与改进方向第十章:统计指数在未来发展趋势与挑战10.1 统计指数发展的新趋势10.1.1 引出统计指数发展的新趋势10.1.2 讲解大数据、等技术对统计指数发展的影响10.1.3 分析新趋势下统计指数的发展机遇与挑战10.2 统计指数在应对现实挑战中的应用10.2.1 介绍统计指数在应对现实挑战中的应用10.2.2 分析统计指数在解决社会经济问题中的作用10.2.3 举例说明统计指数在应对现实挑战中的重要性10.3 统计指数在未来发展的思考与展望10.3.1 讲解统计指数在未来发展中的机遇与挑战10.3.2 探讨统计指数在理论与实践创新中的方向10.3.3 展望统计指数在未来发展中的前景重点解析本文教案主要介绍了统计指数的基本概念、分类、计算方法以及在各个领域的应用。
统计学容许度指数-概述说明以及解释1.引言1.1 概述概述统计学容许度指数是一种用于衡量数据的可靠性和误差程度的指标。
在统计学中,我们常常需要对收集到的数据进行分析和解释,而统计学容许度指数提供了一种衡量数据准确性的方法。
在数据收集和分析过程中,难免会面临各种误差和偏差。
这些误差和偏差可能来自于样本选择的随机性、测量工具的精确度、观察者的主观偏见等等。
因此,我们需要一种客观的指标来评估数据的可靠性,以便更好地理解和利用这些数据。
统计学容许度指数是一种通过对数据进行统计分析、计算和比较的方法来评估数据的准确性和稳定性的指标。
它可以帮助我们衡量数据的误差程度,并确定数据的可靠程度和可信度。
通过统计学容许度指数,我们可以了解数据的可靠性对于分析和决策的影响。
如果数据的容许度指数较高,表示数据的误差较小,我们可以更加自信地使用这些数据进行分析和推断。
相反,如果数据的容许度指数较低,表示数据的误差较大,我们需要对数据进行进一步的检验和修正,以确保分析结果的准确性和可靠性。
在本文中,我们将介绍统计学容许度指数的定义和计算方法,并探讨其应用的价值和未来的发展方向。
通过深入理解和应用统计学容许度指数,我们能够更好地利用统计学的方法和工具,提高数据分析的准确性和可靠性,为决策提供更有效的依据。
1.2 文章结构文章结构部分的内容大致如下:文章结构部分旨在介绍本文的整体组织架构,让读者对文章的内容有一个清晰的概念。
本文共包括引言、正文和结论三个部分。
引言部分将提供对统计学容许度指数的背景和意义进行概述,介绍统计学容许度指数的定义、计算方法以及其在实际应用中的价值和意义。
引言部分还会明确本文的目的,即通过探讨统计学容许度指数的概念和应用,提供一种新的统计分析工具和决策参考。
正文部分将详细阐述统计学的基本概念,包括统计学的定义、原则和基本方法等内容,为读者建立起对统计学基础知识的理解。
接着,本文将专注于统计学容许度指数的定义和计算方法,并介绍其在实际问题中的具体应用。
第十四章 统计指数
1.某企业生产甲、乙两种产品,资料如下:
要求:
(1)计算产量与单位成本个体指数。
(2)计算两种产品产量总指数以及由于产量增加而增加的生产费用。
(3)计算两种产品单位成本总指数以及由于成本降低而节约的生产费用。
解:
(2)产量指数:
%64.11555000
63600
01
0==
∑∑q
z q z (3)单位成本指数:
%84.9963600
63500
1
011==
∑∑q
z q z 2.某商场销售的三种商品资料如下:
要求:
(1)计算三种商品的销售额总指数。
(2)分析销售量和价格变动对销售额影响的绝对值和相对值。
解: (1)销售额总指
数
:
%06.12126000
31475
01
1==
∑∑q
p q p
(2)价格的变动
:
%29.10928800
31475
1
011==
∑∑q
p q
p 销售量的变动:
%77.11026000
28800
01
0==
∑∑q
p q p 3.试根据下列资料分别用拉氏指数和帕氏指数计算销售量指数及价格指数。
解:
价格指数:
%5.92480
444
1
011==
∑∑q
p q p
%76500
380
001==
∑∑q
p q p
销售量指数
%965004800
01
0==
∑∑q
p q p %8.116380
4440111==∑∑q p q p 4.某公司三种产品的有关资料如下表,试问三种产品产量平均增长了多少,产量增长对产值有什么影响
解:
三种产品产量平均增长了25%,由于产量增长使得产值也相应增长了25%,绝对额增加65万元。
5.三种商品销售资料如下,通过计算说明其价格总的变动情况。
价格总指数 %78.8776
.300264
85
.014495.0349.08614434861
1
11
11
011==+
+++=
=
=
∑∑∑∑q
p k q p q
p q p k p
p
三种商品价格平均下降%,绝对额减少万元。
6.某商场上期销售收入为525万元,本期要求达到万元。
在规定销售价格下调%的条件下,该商场商品销售量要增加多少,才能使本期销售达到原定的目标
∴销售量指数%83.108%4.97%1060
01
0=÷==
∑∑q
p q p k q
该商场商品销售量要增加%才能使本期销售达到原定的目标。
7.某地区2003年平均职工人数为万人,比2002年增加2%;2003年工资总额为167076万元,比2002年多支出9576万元。
试推算2002年职工的平均工资。
2002年平均职工人数 = ÷ = 225(万人)
2002年工资总额 = 167076—9576 = 157500(万元)
2002年职工的平均工资=工资总额÷平均职工人数=157500÷225=700元
8.某电子生产企业2003年和2002年三种主要产品的单位生产成本和产量资料如下:
要求:
(1)计算三种产品的产值总指数和产值增减总额。
(2)以2003年的产量为权数计算三种产品的加权单位产品成本综合指数,以及因单位成本变动的产值增减额。
(3)以2002年单位产品成本为权数计算三种产品的加权产量综合指数,以及由于产量变动的产值增减额。
解:
(1)三种产品的产值总指数
%
87.123105150
130250
01
1==
∑∑q
z q
z
产值增减总额
∑∑-=-10
1302500
01
1q
z q z
(2)单位产品成本综合指数
%28.112116000
130250
1
011==
∑∑q
z q z
因单位成本变动的产值增减额()∑∑=-=-元142501160001302501011q z q z (3)三种产品产量综合指数
%32.110105150
116000
01
0==
∑∑q
z q z
由于产量变动的产值增减额()∑∑=-=-元108501051501160000010q z q z
9.某工厂有三个生产车间,基期和报告期各车间的职工人数和劳动生产率资料如下:试分析该企业劳动生产率的变动及其原因。
解: 总水平指
数
:
9732
.618
.60
01
110
1==
=
∑∑∑∑f
f x f f
x x x
组水平变动指数:
%66.10202
.618
.61
1
01
11假定
1
==
=∑∑∑∑f
f x f f x x x 结构变动指数:
%25.9532.602
.60
假定==x x 总水平指数=组水平变动指数×结构变动指数 %=%×%
= + ()
计算结果表明,该企业的劳动生产率报告期比基期下降了2,。
22%,减少1400元,是由于企业结构发生了变动,使得公司的劳动生产率下降%,平均每车间减少3500元;由于各车间劳动生产率的提高,使企业劳动生产率提高了%,平均增加2100元共同作用的结果。
10.某市限购令前后的房价如下:
要求:
(1)计算价格指数。
(2)房价是上升了还是下降了为什么
(1)价格指数
%89.1089000000
9800000
600100002001500060011000200160001
011==⨯+⨯⨯+⨯=
∑∑q
p q p
(2)限购令后该市的房价不但没有下降,反而上升了%,主要原因是均价较低的郊区商品房成交套数增加,并且占全部成交套数的比重由2010年的50%上升到2011年的75%,而均价较高的市区商品房成交套数减少,并且占全部成交套数的比重由2010年的50%下降到2011年的25%。
结构的变化带来该市商品房平均价格下降250元的现象。