应用统计学(第四版)第10章 统计指数

第10章习题答案一、思考题（略）二、选择题1、A；2、B；3、B；4、D；5、A；6、A；7、AB；8、CD；9、CD；10、CD。

三、计算题1、（1）计量单位甲乙丙双件双（2）三种商品的销售额指数与增加额分别为:132.3%与767600元；（3）三种商品物价综合指数为113.13%，由于物价变动对销售额的影响365000元；（4）三种商品的销售量综合指数为116.94，,由于销售量变动对销售额的影响402600元。

2、调和平均数形式计算。

三种商品的综合物价指数为106.5%。

3、销售量增长了15.8%。

4、物价指数为112.36%。

5、今年和去年相比，该市零售总额指数：149.88%；零售价指数：111.5%； 零售量指数：134.42%。

零售量变动对零售额的影响为2960万元；零售价变动对零售额的影响为1330万元。

6、（１）零售物价上涨了7.3%；（２）为维持上年的消费水平，由于零售物价上涨消费者多支出了396亿元； （３）若零售物价保持不变，消费者因提高消费水平导致零售量增长而增加的零售额为475亿元。

7、物价上涨使食品销售额增加510.77万元；食品销售量变化使销售额增加273.31万元。

8、该地区3种水果的价格指数为：96.09%；由于价格变动使居民开支减少5.29万元。

9、解：编制计算表如下表10-7（a ）所示。

表10-7（a ） 某厂成本指数计算表４５ ５２ 产品的总平均成本(z )=[∑产品单位成本（z ）×产品产量(q)]/∑产品产量(q) 产品的总平均成本指数=产品结构变动指数×产品单位成本变动指数1110111111000000110z q q z q q z q q z z q qz q q z q qz ==⨯∑∑∑∑∑∑∑∑∑∑∑∑48.1853000110057500110053000110051.393700072037000720575001100==⨯93.96%=101.71%×92.18%从产品单位成本变动水平看：产品的总平均成本变动=产品结构变动对产品总平均成本的影响+产品单位成本变动对产品总平均成本的影响110001001101101111()()z q z q z q z q z q z q z z q qq qq q -=-=-+-∑∑∑∑∑∑∑∑∑∑∑∑53000370005750037000530005750048.1851.39()()1100720110072011001100-=-=-+- －3.21 = 0.89 +（－4.10）评价：该公司的产品总平均成本报告期比基期降低了6.24%，平均每件单位成本下降了3.21元。

第十章统计指数一、填空题1．狭义指数是反映复杂现象总体变动的2.指数按其所反映的对象范围的不同，分为指数和指数。

3.指数按其所标明的指标性质的不同，分为指数和指数。

4.指数按其采用基期的不同，分为指数和指数。

5. 指数是在简单现象总体条件下存在的，指数是在复杂现象总体的条件下进行编制的。

6.总指数的计算形式有两种，一种是指数，一种是指数。

7.按照一般原则，编制数量指标指数时，同度量因素固定在，编制质量指标指数时，同度量因素固定在。

8.在编制质量指标指数时，指数化指标是指标，同度量因素是与之相联系的指标。

9.综合指数编制的特点，一是选择与指标相联系的同度量因素，二是把同度量因素的时期。

10.拉氏指数对于任何指数化指标的同度量因素都固定在，派氏指数对于任何指数化指标的同度量因素都固定在。

11.编制指数的一般方法是：指数是按拉氏指数公式编制的；指数是按派氏指数公式编制的。

12．综合指数的编制方法是先后。

13．编制综合指数时，与指数化指标相联系的因素称，还可以称为。

14.平均指数的计算形式为指数和指数。

15.平均指数是先计算出数量指标或质量指标的指数，然后再进行计算，来测定现象的总变动程度。

16.在编制平均指数时，算术平均数指数多用为权数，调和平均数指数多用为权数。

17.数量指标的算术平均数指数，在采用为权数的特定条件下，和一般综合指数的计算结论相同；而质量指标的调和平均数指数，在采用为权数的特定条件下，计算结果和综合指数一致。

18.编制数量指标平均指数，一是掌握，二是掌握。

19.编制质量指标平均指数，一是掌握，二是掌握。

20.在零售物价指数中，K表示，W表示。

21.平均指数既可依据资料编制，也可依据资料编制，同时还可用估算的权数比重进行编制计算。

22.因素分析包括数和数分析。

23.总量指标二因素分析是借助于来进行，即当总量指标是两个原因指标的时，才可据此进行因素分析。

24指数体系中，指数之间的数量对等关系表现在两个方面：一是结果指数等于因素指数的，二是结果指数的分子分母之差等于各因素指数的。

《应用统计学》教学大纲一、课程简介统计学是农林经济管理本科专业的一门学科基础必修课。

本课程采取理论讲授与实验操作交替进行的方式，理论讲授部分主要包括统计数据的收集、整理、分析及预测，重点讲授各种统计方法，如参数估计、假设检验、方差分析、时间序列分析、统计指数、相关与回归分析等；实验操作部分包括统计工作过程的实验、Excel等电子表格在统计分析中的应用、统计学知识的综合应用三个实验。

二、教学大纲1.教学目的开设此课旨在培养学生数据收集、处理和分析能力。

通过本课程的学习，学生掌握统计学基本理论、方法及在Excel等统计软件中的运用，达到能应用统计方法分析问题和解决问题的目的。

2.教学要求（1）对教师的要求教师要积极备课，认真准备实验，对课程内容要融会贯通，切忌照本宣科。

授课在多媒体教室，结合典型实用案例和相关统计软件，理论讲授与上机操作交替进行。

做到授课内容与大纲相符，注重全程考核，最终成绩由考勤、调查方案设计、实验报告撰写、调查报告撰写、上机测试及期末考试构成，成绩评价体系标准真实、严谨、公平、公正、公开，提升学生学习积极性。

（2）对学生的要求学生能系统地掌握各种统计方法，并理解各种统计方法中所包含的统计思想；能运用统计方法分析和解决实际问题的能力；能够熟练应用Excel等统计软件进行数据分析。

3.预备知识或先修课程要求先修课程包括《概论论与数理统计》、《微观经济学》、《宏观经济学》、《管理学原理》等。

4.教学方式课程包括理论讲授和实验操作两部分。

理论授课32学时，教师讲授与课堂讨论相结合；实验操作24学时，包括统计工作过程实验、Excel等统计软件的运用及统计学知识的综合运用，以学生上机操作为主，教师引导、实地调查为辅。

5.实验环境和设备1)硬件环境：每个学生一台微型计算机。

2)软件环境：Windows 7、Office 2007（或以上版本）（Excel需安装数据分析及规划求解功能）软件包、卓越班学生还需SPSS、DPS软件包。

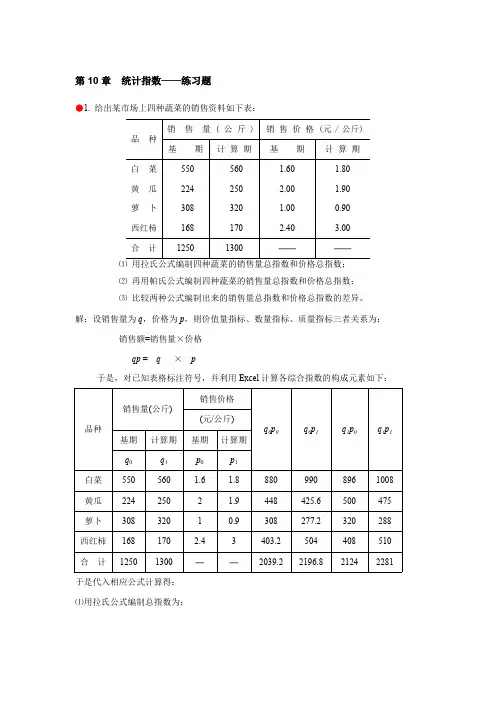
第10章统计指数——练习题●1. 给出某市场上四种蔬菜的销售资料如下表：销售量 ( 公斤 )销售价格 (元/公斤)品种基期计算期基期计算期白菜550560 1.60 1.80黄瓜224250 2.00 1.90萝卜308320 1.000.90西红柿168170 2.40 3.00合计12501300────⑴用拉氏公式编制四种蔬菜的销售量总指数和价格总指数；⑵再用帕氏公式编制四种蔬菜的销售量总指数和价格总指数；⑶比较两种公式编制出来的销售量总指数和价格总指数的差异。

解：设销售量为q，价格为p，则价值量指标、数量指标、质量指标三者关系为：销售额=销售量×价格qp = q×p于是，对已知表格标注符号，并利用Excel计算各综合指数的构成元素如下：销售价格销售量(公斤)(元/公斤)q0p0q0p1q1p0q1p1品种基期计算期基期计算期q0q1p0p1白菜550560 1.6 1.88809908961008黄瓜2242502 1.9448425.6500475萝卜30832010.9308277.2320288西红柿168170 2.43403.2504408510合计12501300──2039.22196.821242281于是代入相应公式计算得：⑴用拉氏公式编制总指数为：四种蔬菜的销售量总指数 10002124104.16% ,2039.2q q p L q p===∑∑四种蔬菜的价格总指数12196.8107.73%2039.2p q p L q p===∑∑ ⑵ 用帕氏公式编制总指数：四种蔬菜的销售量总指数为 1112281103.83%2196.8q q p P q p===∑∑四种蔬菜的价格总指数为 1112281107.39%2124pq p P q p===∑∑⑶ 比较两种公式编制出来的销售量总指数和价格总指数，可见：拉氏指数＞帕氏指数 在经济意义上，拉氏指数将同度量因素固定在基期。

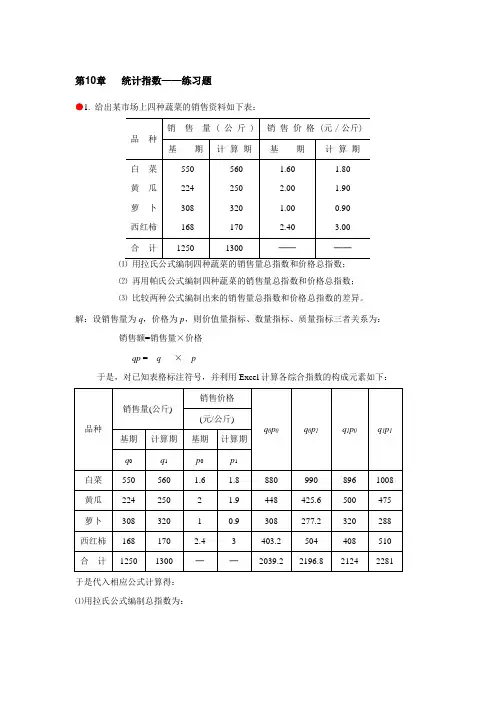
第10章统计指数——练习题●1. 给出某市场上四种蔬菜的销售资料如下表：⑵再用帕氏公式编制四种蔬菜的销售量总指数和价格总指数；⑶比较两种公式编制出来的销售量总指数和价格总指数的差异。

解：设销售量为q，价格为p，则价值量指标、数量指标、质量指标三者关系为：销售额=销售量×价格qp = q×p于是，对已知表格标注符号，并利用Excel计算各综合指数的构成元素如下：于是代入相应公式计算得：⑴用拉氏公式编制总指数为：四种蔬菜的销售量总指数 10002124104.16% , 2039.2q q p L q p===∑∑四种蔬菜的价格总指数 0102196.8107.73%2039.2p q p L q p===∑∑⑵ 用帕氏公式编制总指数：四种蔬菜的销售量总指数为 11012281103.83% 2196.8q q p P q p===∑∑四种蔬菜的价格总指数为 1112281107.39%2124pq p P q p===∑∑ ⑶ 比较两种公式编制出来的销售量总指数和价格总指数，可见：拉氏指数＞帕氏指数 在经济意义上，拉氏指数将同度量因素固定在基期。

销售量总指数说明消费者为保持与基期相同的消费价格，因调整增减的实际购买量而导致实际开支增减的百分比；价格总指数说明消费者为购买与基期相同数量的四种蔬菜，因价格的变化而导致实际开支增减的百分比。

帕氏指数将同度量因素固定在计算期。

销售量总指数说明消费者在计算期购买的四种蔬菜，因销售量的变化而导致实际开支增减的百分比；价格总指数说明消费者在计算期实际购买的四种蔬菜，因价格的变化而导致实际开支增减的百分比。

●2.依据上题的资料，试分别采用埃奇沃斯公式、理想公式和鲍莱公式编制销售量指数；然后，与拉氏指数和帕氏指数的结果进行比较，看看它们之间有什么关系。

解：采用埃奇沃斯公式编制销售量指数为：1011011101()()212422814405103.9896%2039.22196.84236q q pp q p q p E q pp q p q p++==+++===+∑∑∑∑∑∑采用理想公式编制销售量指数为：103.994869%q F ===采用鲍莱公式编制销售量指数为：1011000111()()22104.16%103.83%104.00%2q q q q p q p B L P q p q p =+=++==∑∑∑∑与拉氏销售量指数和帕氏销售量指数的结果进行比较，它们之间的关系是： q q q q q L B F E P >>>>即拉氏销售量指数最大，鲍莱销售量指数次大，理想销售量指数居中，埃奇沃斯销售量指数较小，帕氏销售量指数最小。

应用统计学教案-统计指数第一章：统计指数概述1.1 指数的概念与分类1.1.1 复习指数的概念1.1.2 区分算术指数与几何指数1.1.3 引出统计指数的概念1.2 统计指数的性质与作用1.2.1 阐述统计指数的基本性质1.2.2 解释统计指数在经济学、社会学科等领域的应用1.2.3 强调统计指数在数据分析与决策中的重要性1.3 统计指数的编制方法1.3.1 介绍拉氏指数与帕氏指数的编制方法1.3.2 分析两种指数的优缺点及其适用场景1.3.3 演示编制简单统计指数的实例第二章：个体指数与综合指数2.1 个体指数的概念与计算2.1.1 引出个体指数的概念2.1.2 讲解个体指数的计算方法2.1.3 举例说明个体指数在实际应用中的作用2.2 综合指数的概念与计算2.2.1 介绍综合指数的概念2.2.2 阐述综合指数的计算方法2.2.3 分析综合指数在分析现象总体变动中的作用2.3 指数体系与同度量因素2.3.1 讲解指数体系的概念与构成2.3.2 阐释同度量因素的作用与选择原则2.3.3 举例说明同度量因素在实际应用中的重要性第三章：统计指数的计算与应用3.1 平均数指数的计算3.1.1 引出平均数指数的概念3.1.2 讲解平均数指数的计算方法3.1.3 演示计算平均数指数的实例3.2 链式指数的计算与应用3.2.1 介绍链式指数的概念与计算方法3.2.2 阐述链式指数在分析现象长期变动中的作用3.2.3 举例说明链式指数在实际应用中的重要性3.3 统计指数在实际应用中的案例分析3.3.1 分析消费者价格指数（CPI）的计算与作用3.3.2 讲解生产者价格指数（PPI）的计算与作用3.3.3 探讨统计指数在其他领域的应用实例第四章：统计指数的分析与评价4.1 统计指数分析的方法与技巧4.1.1 引出统计指数分析的方法与技巧4.1.2 讲解比较分析、因素分析等方法在统计指数分析中的应用4.1.3 演示统计指数分析的实例4.2 统计指数评价的标准与原则4.2.1 阐述统计指数评价的标准与原则4.2.2 分析评价标准与原则在实际应用中的重要性4.2.3 讨论评价标准与原则的局限性与改进方向4.3 统计指数在政策制定与决策中的应用4.3.1 讲解统计指数在政策制定与决策中的作用4.3.2 分析统计指数在国民经济核算、价格调控等领域的应用实例4.3.3 探讨统计指数在决策过程中的优化与改进第五章：统计指数的拓展与应用5.1 统计指数与经济预测5.1.1 引出统计指数在经济预测中的应用5.1.2 讲解经济预测方法与统计指数的结合5.1.3 演示统计指数在经济预测中的实例5.2 统计指数与大数据分析5.2.1 介绍大数据时代统计指数的新发展5.2.2 阐述大数据分析技术与统计指数的结合5.2.3 探讨大数据时代统计指数在决策支持中的作用与挑战5.3 统计指数在其他领域的应用5.3.1 分析统计指数在社会科学、环境科学等领域的应用实例5.3.2 讲解统计指数在其他领域的拓展与应用5.3.3 展望统计指数在未来发展中的前景与挑战第六章：指数平滑法在统计指数中的应用6.1 指数平滑法的基本原理6.1.1 引出指数平滑法6.1.2 讲解指数平滑法的基本原理6.1.3 演示计算指数平滑法的实例6.2 指数平滑法在统计指数中的应用6.2.1 介绍指数平滑法在统计指数中的应用6.2.2 阐述指数平滑法在时间序列预测中的优势6.2.3 举例说明指数平滑法在实际应用中的重要性6.3 指数平滑法的拓展与改进6.3.1 讲解指数平滑法的拓展与改进6.3.2 分析拓展与改进在提高预测精度中的作用6.3.3 探讨指数平滑法在实际应用中的局限性与改进方向第七章：多元统计指数分析7.1 多元统计指数的概念与分类7.1.1 引出多元统计指数的概念7.1.2 区分不同类型的多元统计指数7.1.3 阐述多元统计指数在分析多因素变动中的作用7.2 多元统计指数的计算方法7.2.1 讲解多元统计指数的计算方法7.2.2 分析各种计算方法的优缺点及其适用场景7.2.3 演示计算多元统计指数的实例7.3 多元统计指数在实际应用中的案例分析7.3.1 分析多元统计指数在市场分析、产品质量评价等领域的应用实例7.3.2 讲解多元统计指数在实际应用中的重要性7.3.3 探讨多元统计指数在解决实际问题中的局限性与改进方向第八章：统计指数与国民经济核算8.1 国民经济核算体系与统计指数8.1.1 引出国民经济核算体系与统计指数的关系8.1.2 讲解国民经济核算体系的基本概念与方法8.1.3 阐述统计指数在国民经济核算中的应用8.2 国内生产总值（GDP）的统计指数分析8.2.1 介绍国内生产总值（GDP）的概念与计算方法8.2.2 分析统计指数在GDP计算与分析中的应用8.2.3 举例说明统计指数在GDP分析中的重要性8.3 国民经济其他指标的统计指数分析8.3.1 分析消费价格指数（CPI）、生产价格指数（PPI）等指标的统计指数应用8.3.2 讲解统计指数在其他国民经济指标分析中的应用实例8.3.3 探讨统计指数在国民经济分析中的局限性与改进方向第九章：统计指数在金融领域的应用9.1 统计指数在金融市场分析中的应用9.1.1 引出统计指数在金融市场分析中的应用9.1.2 讲解金融市场指数的编制与分析方法9.1.3 阐述统计指数在金融市场分析中的重要性9.2 统计指数在金融风险管理中的应用9.2.1 介绍统计指数在金融风险管理中的应用9.2.2 分析统计指数在风险评估、预警等方面的作用9.2.3 举例说明统计指数在金融风险管理中的重要性9.3 统计指数在其他金融领域的应用9.3.1 分析统计指数在信用评级、资产定价等领域的应用实例9.3.2 讲解统计指数在其他金融领域的应用与价值9.3.3 探讨统计指数在金融领域发展的局限性与改进方向第十章：统计指数在未来发展趋势与挑战10.1 统计指数发展的新趋势10.1.1 引出统计指数发展的新趋势10.1.2 讲解大数据、等技术对统计指数发展的影响10.1.3 分析新趋势下统计指数的发展机遇与挑战10.2 统计指数在应对现实挑战中的应用10.2.1 介绍统计指数在应对现实挑战中的应用10.2.2 分析统计指数在解决社会经济问题中的作用10.2.3 举例说明统计指数在应对现实挑战中的重要性10.3 统计指数在未来发展的思考与展望10.3.1 讲解统计指数在未来发展中的机遇与挑战10.3.2 探讨统计指数在理论与实践创新中的方向10.3.3 展望统计指数在未来发展中的前景重点解析本文教案主要介绍了统计指数的基本概念、分类、计算方法以及在各个领域的应用。