对称分量法

对称分量法公式摘要：一、对称分量法简介1.对称分量法的概念2.应用背景二、对称分量法公式推导1.基本概念与定义2.公式推导过程三、对称分量法的应用1.在电力系统中的应用2.在其他领域的应用四、对称分量法的优缺点1.优点2.缺点五、结论正文：对称分量法是一种分析电气工程、信号处理等领域中复杂系统的方法，通过分解系统中的对称分量，简化问题，从而更好地理解和处理问题。

对称分量法广泛应用于电力系统的故障分析、保护装置设计和运行控制等领域。

1.对称分量法的概念对称分量法是将复杂系统中各变量分解为正、负、零三个对称分量。

正分量表示变量在正序方向上的分量，负分量表示变量在负序方向上的分量，零分量表示变量在零序方向上的分量。

通过分解对称分量，可以简化系统模型，便于分析和处理问题。

2.应用背景对称分量法主要应用于电力系统，包括发电、输电、配电和用电等环节。

在电力系统中，对称分量法可以帮助分析系统中的不对称故障，如两相或三相短路等，并为保护装置的设计和运行提供依据。

此外，对称分量法还应用于信号处理、自动控制、通信等领域。

3.对称分量法公式推导对称分量法的公式推导主要包括基本概念与定义以及公式推导过程。

首先，根据系统中的变量和其正、负、零序分量的关系，可以得到对称分量法的定义。

然后，通过对称分量法的定义，推导出各个分量的计算公式。

4.对称分量法的应用对称分量法在电力系统中的应用主要包括故障分析、保护装置设计和运行控制等。

在故障分析中，通过计算系统中的对称分量，可以判断故障的类型和位置。

在保护装置设计中，根据系统中的对称分量，可以设计出合适的保护装置。

在运行控制中，通过对称分量法，可以实现对电力系统的实时监控和控制。

5.对称分量法的优缺点对称分量法的优点在于能够简化复杂系统的分析过程，便于理解和处理问题。

然而，对称分量法也存在一定的缺点，如在实际应用中，可能需要根据具体情况对对称分量法进行修正。

对称分量法一、什么是对称分量法对称分量法（Symmetrical Component Method，简称SCM）是一种用于解决三相电力系统中不平衡故障问题的分析方法。

在电力系统中，由于各种原因（例如电力负载变化、设备故障等），电源产生的三相电流和电压可能会失去平衡，从而引发各种故障。

对称分量法通过将不平衡信号分解为对称和非对称分量，可以准确地计算电力系统中发生的不平衡故障。

二、对称分量法的基本原理2.1 对称分量的定义在对称分量法中，将三相电源的电压和电流分解为正序、负序和零序三个互相独立的分量。

正序分量表示电压和电流的幅值和相位全都相同，负序分量表示电压和电流的幅值相同但相位互差120度，零序分量表示电压和电流的幅值都为零。

2.2 不平衡故障的分析利用对称分量法，可以将不平衡故障分解为正序、负序和零序三个分量。

通过分析这三个分量在电力系统中的传输和变化，可以准确地确定故障的发生位置和类型。

2.3 对称分量的计算方法对称分量的计算主要基于对称分量正负序的定义和性质。

对于三相对称装置，其中包括电源和电路中没有接地的中性点，正序分量可以通过直接测量获得；负序分量可以通过将三相电流线电压和120度相位互差的关系应用于电压计算得到；零序分量可以通过将三相电压和电流进行相加、平均得到。

三、对称分量法的应用3.1 故障分析与检测对称分量法广泛应用于电力系统中不平衡故障的分析与检测。

通过分析电力系统中各个节点的对称分量，可以判断故障的类型、发生位置以及对系统的影响程度。

这对于保护装置的及时动作以及减小故障对电力系统的影响具有重要意义。

3.2 故障定位与隔离利用对称分量法，可以准确地定位和隔离电力系统中的故障。

通过分析故障点处不同分量的幅值和相位变化，可以确定故障的位置，并采取相应的措施进行隔离和修复。

这可以减少故障造成的停电时间和电力系统的恢复成本。

3.3 电力系统设计和优化对称分量法对于电力系统的设计和优化也具有重要意义。

对称分量法对称分量法是一种强大的数学工具，它可以用来解决各种数学问题，既可以解决大型线性方程组也可以解决高阶非线性方程组。

它的历史可以追溯到古希腊时期，但它的最初形式可以追溯到17世纪的苏格兰数学家詹姆斯拉瓦锡（James Gregory）和英格兰数学家伯纳德罗比（Bernard Robins）。

这种方法的基本思想是用一组标准的的符号，可以用来表示不同的数学结构，这样就可以用不同的语言来解释不同的数学模型。

基本上就是找到一组可以表示和解释不同物理或数学结构的符号。

在一维空间中，只需要表示一个结构，在多维空间中，就需要多个符号来表示。

对称分量法的优点是可以用简单的符号语言来描述各种复杂的几何结构，它可以将模型简化，使其易于推理和理解。

由于它可以通过几何结构定义来表示不同的数学模型，因此它可以用来研究各种大型系统，包括力学、热力学和流体力学等，从而更好地描述和分析它们。

同时，对称分量法也可以用来解决更简单的问题，比如最优化问题和矩阵方程组。

它可以根据解的精度来改变相应的迭代阶数，从而获得最佳的解。

例如，可以用来解决高阶多项式的求根问题，也可以用来解决线性规划问题，这是由于它可以根据精度改变迭代步骤，这样可以使解更具有准确性。

另外，对称分量法也可以提供一种更有效的数值计算方法。

通过它可以实现更快的计算速度，因此可以解决更复杂的问题，比如解决多维的线性或非线性方程组。

总之，对称分量法是一种强大的数学工具，它可以用来解决各种复杂的数学问题，包括大型线性方程组、非线性方程组和最优化问题等。

它可以通过几何结构定义将复杂的模型简化，从而使模型易于推理和理解，并使计算更加高效。

此外，由于它可以根据解的精度来改变迭代步骤，因此可以提供有效的数值计算方法。

因此，对称分量法在许多领域都具有重要的理论意义和应用价值。

对称分量法公式摘要：一、对称分量法简介1.对称分量法的概念2.对称分量法在工程中的应用二、对称分量法公式推导1.基本电路分析2.对称分量法的推导过程3.对称分量法公式三、对称分量法应用实例1.三相电路分析2.发电机和变压器分析3.其他应用场景四、对称分量法的优缺点1.优点2.缺点正文：一、对称分量法简介对称分量法是一种电路分析方法，主要用于解决不对称三相电路的问题。

该方法将三相电路分解为三个独立的单相电路，通过对每个单相电路的分析，可以得到三相电路中各相的电流和电压。

对称分量法广泛应用于电力系统、自动化控制等领域。

二、对称分量法公式推导1.基本电路分析首先，我们分析一个简单的不对称三相电路，包含三个相电压U1、U2、U3 和一个中性线N。

我们用矢量表示电压和电流：U1、U2、U3 和I1、I2、I3。

2.对称分量法的推导过程为了方便分析，我们将电压和电流分解为正序和负序两个分量。

正序分量表示三相电压和电流的平衡部分，负序分量表示三相电压和电流的不平衡部分。

正序分量和负序分量的关系如下：U1p = U1 + U2 + U3I1p = I1 + I2 + I3U1n = U1 - U2 - U3I1n = I1 - I2 - I3其中，U1p、I1p 表示正序分量的电压和电流，U1n、I1n 表示负序分量的电压和电流。

3.对称分量法公式根据对称分量法，我们可以得到以下公式：U1p = U1 + jU2 + jU3I1p = I1 + jI2 + jI3U1n = U1 - jU2 - jU3I1n = I1 - jI2 - jI3其中，j 表示虚数单位。

三、对称分量法应用实例1.三相电路分析通过对称分量法，我们可以将复杂的不对称三相电路分解为三个简单的单相电路。

这样，我们可以分别分析每个单相电路，从而简化电路分析过程。

2.发电机和变压器分析对称分量法广泛应用于发电机和变压器的分析。

通过分解发电机和变压器的不对称电流和电压，我们可以了解设备的运行状态，及时发现故障，保证电力系统的稳定运行。

对称分量法(零序,正序,负序)的理解与计算对称分量法（零序，正序，负序）的理解与计算1）求零序分量：把三个向量相加求和。

即A相不动，B相的原点平移到A相的顶端（箭头处），注意B相只是平移，不能转动。

同方法把C相的平移到B相的顶端。

此时作A相原点到C相顶端的向量（些时是箭头对箭头），这个向量就是三相向量之和。

最后取此向量幅值的三分一，这就是零序分量的幅值，方向与此向量是一样的。

2）求正序分量：对原来三相向量图先作下面的处理：A相的不动，B相逆时针转120度，C相顺时针转120度，因此得到新的向量图。

按上述方法把此向量图三相相加及取三分一，这就得到正序的A相，用A相向量的幅值按相差120度的方法分别画出B、C两相。

这就得出了正序分量。

3）求负序分量：注意原向量图的处理方法与求正序时不一样。

A相的不动，B 相顺时针转120度，C相逆时针转120度，因此得到新的向量图。

下面的方法就与正序时一样了。

对电机回路来说是三相三线线制，Ia+Ib+Ic=0，三相不对称时也成立；当Ia+Ib+Ic≠0时必有一相接地，对地有有漏电流；对三相四线制则为Ia+Ib+Ic+Io=0成立，只要无漏电，三相不对称时也成立；因此，零序电流通常作为漏电故障判断的参数。

负序电流则不同，其主要应用于三相三线的电机回路；在没有漏电的情况下（即Ia+Ib+Ic=0），三相不对称时也会产生负序电流；负序电流常作为电机故障判断；注意了：Ia+Ib+Ic=0与三相对称不是一回事；Ia+Ib+Ic=0时，三相仍可能不对称。

注意了：三相不平衡与零序电流不可混淆呀！三相不平衡时，不一定会有零序电流的；同样有零序电流时，三相仍可能为对称的。

（这句话对吗?）前面好几位把两者混淆了吧！正序、负序、零序的出现是为了分析在系统电压、电流出现不对称现象时，把三相的不对称分量分解成对称分量（正、负序）及同向的零序分量。

只要是三相系统，一般针对三相三线制的电机回路，就能分解出上述三个分量（有点象力的合成与分解，但很多情况下某个分量的数值为零）。

对称分量法之宇文皓月创作正序：A相领先B相120度，B相领先C相120度，C相领先A 相120度。

负序：A相落后B相120度，B相落后C相120度，C相落后A 相120度。

零序：ABC三相相位相同，哪一相也不领先，也不落后。

三相短路故障和正常运行时，系统里面是正序。

单相接地故障时候，系统有正序、负序和零序分量。

两相短路故障时候，系统有正序和负序分量。

两相短路接地故障时，系统有正序、负序和零序分量称分量法基本概念和简单计算正常运行的电力系统，三相电压、三相电流均应基本为正相序，根据负荷情况（感性或容性），电压超前或滞后电流1个角度（Φ），如图1。

图1：正常运行的电力系统电压电流矢量图对称分量法是分析电力系统三相不服衡的有效方法，其基本思想是把三相不服衡的电流、电压分解成三组对称的正序相量、负序相量和零序相量，这样就可把电力系统不服衡的问题转化成平衡问题进行处理。

在三相电路中，对于任意一组分歧错误称的三相相量（电压或电流），可以分解为3组三相对称的分量。

图2：正序相量、负序相量和零序相量（以电流为例）当选择A相作为基准相时，三相相量与其对称分量之间的关系（如电流）为：IA=Ia1+Ia2+Ia0――――――――――――――――――――――――――○1IB=Ib1+Ib2+Ib0=α2Ia1+αIa2 + Ia0――――――――――○2IC=Ic1+Ic2+Ic0=α Ia1+α2 Ia2+Ia0―――――――――――○3对于正序分量：Ib1=α2 Ia1 ，Ic1=αIa1对于负序分量：Ib2=αIa2 ，Ic2=α2Ia2对于零序分量：Ia0= Ib0 = Ic0 式中，α为运算子，α=1∠120°有α2＝1∠240°, α3＝1, α+α2+1=0 由各相电流求电流序分量：I1=Ia1= 1/3(IA +αIB +α2 IC) I2=Ia2= 1/3(IA +α2IB +αIC) I0=Ia0= 1/3(IA +IB +IC) 以上3个等式可以通过代数方法或物理意义（方法）求解。

对称分量法
一、概述
1918年，加拿大电气学家Charles LeGeyt Fortescue发明对称分量法（method of symmetrical components），对称分量法（method of symmetrical components）将一个不对称的三个相量，分解为三组对称的相量：正序分量、负序分量和零序分量，对称分量法广泛应用于三相交流电参量的不对称程度分析。

二、计算
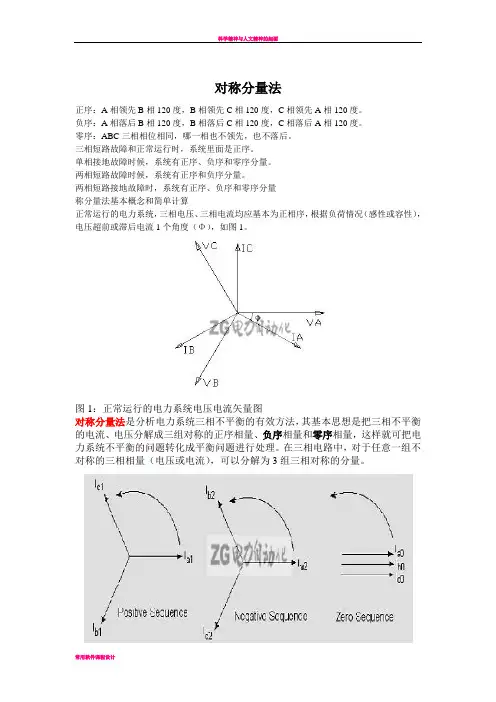
下图的图a、b、c分别表示三组对称的三相相量：
1、不对称分量的合成
幅值相等，相位依次差120°，称为正序分量；
幅值相等，相位依次差120°，相序与正序分量相反，称为负序分量；
幅值和相位均相等，称为零序分量。

将上述三组对称的三相相量相加，得到一组不对称的三相相量，不对称的三相相量的数学表达式为：
( 1)
由对称性，参见图a、图b、图c，可知：
(2)
式(2)代入式(1)可得：
(3)
2、不对称分量的分解
式(3)的逆关系为：
上式说明三个不对称的相量可以唯一地分解成为三组对称的相量，即对称分量:正序分量、负序分量和零序分量。

三、应用
对称分量法常用于电力系统的三相不对称分析，国标《GB/T15543-2008电能质量三相电压不平衡》定义的三相电压不平衡度就是采用三相电压的负序分量与正序分量的比值或零序分量与正序分量的比值表示。

WP4000变频功率分析仪依据国标要求，求解三相电参量的基波分量的三相不平衡度。

为了简便运算，国际上还有另外一些相关标准对不平衡度计算采取其它的更为简化的运算方式。

详细请参见银河百科：三相不平衡度。

对称分量法正序：A相领先B相120度，B相领先C相120度，C相领先A相120度。

负序：A相落后B相120度，B相落后C相120度，C相落后A相120度。

零序：ABC三相相位相同，哪一相也不领先，也不落后。

三相短路故障和正常运行时，系统里面是正序。

单相接地故障时候，系统有正序、负序和零序分量。

两相短路故障时候，系统有正序和负序分量。

两相短路接地故障时，系统有正序、负序和零序分量称分量法基本概念和简单计算正常运行的电力系统，三相电压、三相电流均应基本为正相序，根据负荷情况（感性或容性），电压超前或滞后电流1个角度（Φ），如图1。

图1：正常运行的电力系统电压电流矢量图对称分量法是分析电力系统三相不平衡的有效方法，其基本思想是把三相不平衡的电流、电压分解成三组对称的正序相量、负序相量和零序相量，这样就可把电力系统不平衡的问题转化成平衡问题进行处理。

在三相电路中，对于任意一组不对称的三相相量（电压或电流），可以分解为3组三相对称的分量。

图2：正序相量、负序相量和零序相量（以电流为例）当选择A相作为基准相时，三相相量与其对称分量之间的关系（如电流）为：IA=Ia1+Ia2+Ia0――――――――――――――――――――――――――○1IB=Ib1+Ib2+Ib0=α2Ia1+αIa2 + Ia0――――――――――○2IC=Ic1+Ic2+Ic0=α Ia1+α2Ia2+Ia0―――――――――――○3对于正序分量：Ib1=α2 Ia1 ，Ic1=αIa1对于负序分量：Ib2=αIa2 ，Ic2=α2Ia2对于零序分量：Ia0= Ib0 = Ic0式中，α为运算子，α=1∠120°有α2＝1∠240°, α3＝1, α+α2+1=0由各相电流求电流序分量：I1=Ia1= 1/3(IA +αIB +α2 IC)I2=Ia2= 1/3(IA +α2IB +αIC)I0=Ia0= 1/3(IA +IB +IC)以上3个等式可以通过代数方法或物理意义（方法）求解。

对称分量法对称分量法（method of symmetrical components）电工中分析对称系统不对称运行状态的一种基本方法。

广泛应用于三相交流系统参数对称、运行工况不对称的电气量计算。

电力系统正常运行时可认为是对称的，即各元件三相阻抗相同，各自三相电压、电流大小相等，具有正常相序。

电力系统正常运行方式的破坏主要与不对称故障或者断路器的不对称操作有关。

由于整个电力系统中只有个别点是三相阻抗不相等，所以一般不使用直接求解复杂的三相不对称电路的方法，而采用更简单的对称分量法进行分析。

任何不对称的三相相量A，B，C 可以分解为三组相序不同的对称分量：①正序分量A1，B1，C1，②负序分量A2，B2，C2，③零序分量A，B，C。

即存在如下关系：（1）每一组对称分量之间的关系为（2）式中，复数算符．．．．a＝e j120。

将（２）代入（１）可得；（3）式中系数矩阵是非奇异的，其逆矩阵存在，所以有（4）任意不对称的电压、电流都可以用式（4）求出它们的正序、负序和零序电压、电流分量。

已知三序分量时，又可用式（3）合成三相向量。

在计算电力系统不平衡情况下引用了对称分量法，即任何三相不平衡的电流、电压或阻抗都可以分解成为三个平衡的相量成分即正相序（UA1、UB1、UC1）、负相序（UA2、UB2、UC2）和零相序（UA0、UB0、UC0），即有：UA=UA1+UA2+UA0，UB=UB1+UB2+UB0，UC=UC1+UC2+UC0，其正相序的相序（顺时方向）依次为UA1、UB1、UC1，大小相等，互隔120度；负相序的相序（逆时方向）依次为UA2、UB2、UC2，大小相等，互隔120度；零相序大小相等且同相，各相序都是按逆时针方向旋转。

在对称分量法中引用算子a ，其定义是单位相量依逆时针方向旋转120度，则有：UA0=1/3（UA+UB+UC ），UA1=1/3（UA+aUB+aaUC ），UA2=1/3（UA+aaUB+aUC ）注意以上都是以A 相为基准，都是矢量计算。

对称分量法对称分量法(SymmetricComponentMethod，SCM)是一种复杂现实系统分析方法。

它广泛应用于计算机、软件工程、机器人控制以及其他工业领域的系统分析和控制研究。

它的基本思想是分析一个系统的不同部分，把这些部分归纳为六大类：位置、运动、动力、接口、能量和信息。

这些类别的组合就形成了系统的多层模型，它们能够帮助科学家、工程师、程序员和其他研究者更好地理解和控制现实世界中复杂系统的行为。

系统分析中，对称分量法是用来描述和分析实际系统的一种有效方法。

它假定实际系统可以划分为六个基本部分，即位置、运动、动力、接口、能量和信息。

这样做的优点是，它可以将系统的复杂性减少到六个维度，这样用户就可以对系统进行更容易理解、更加准确的分析。

首先，对位置分量进行分析，即系统中各单元及其连接形式的描述。

其次，对运动分量进行分析，其包括各单元之间的动态关系、各单元的运动特性。

第三，对动力分量进行分析，它能够描述系统中不同部件之间的力学关系，如摩擦力、弹性力等。

第四，对接口分量进行分析，它包括系统的不同单元之间的物理接口，如接头、接线等。

第五，对能量分量进行分析，它能够描述系统中的能量流动，如电信号、声音等。

最后，对信息分量进行分析，它能够描述系统中不同单元之间的信息流动，如指令、数据等。

对称分量法在计算机、软件工程、机器人控制及其他工业领域扮演着重要的角色，它帮助人们更好地理解和控制复杂现实世界中的系统行为。

此外，它还能够帮助用户更准确地建立计算机系统结构、软件设计、机器人控制等，从而更好地满足现有的实际需求。

对称分量法的应用随着科学技术的进步而不断发展，它将会为计算机系统、软件设计、机器人控制等提供更完善的分析和控制方法，从而为科学技术的进步继续做出积极的贡献。

对称重量法（零序，正序，负序）的了解与计算之公保含烟创作1）求零序重量：把三个向量相加求和.即A相不动，B相的原点平移到A相的顶端（箭头处），注意B相只是平移，不能转动.同办法把C相的平移到B相的顶端.此时作A相原点到C相顶端的向量（些时是箭头对箭头），这个向量就是三相向量之和.最后取此向量幅值的三分一，这就是零序重量的幅值，方向与此向量是一样的.2）求正序重量：对原来三相向量图先作下面的处置：A相的不动，B相逆时针转120度，C相顺时针转120度，因此失掉新的向量图.按上述办法把此向量图三相相加及取三分一，这就失掉正序的A相，用A相向量的幅值按相差120度的办法辨别画出B、C两相.这就得出了正序重量.3）求负序重量：注意原向量图的处置办法与求正序时纷歧样.A 相的不动，B相顺时针转120度，C相逆时针转120度，因此失掉新的向量图.下面的办法就与正序时一样了.对电机回路来说是三相三线线制，Ia+Ib+Ic=0，三相分歧毛病称时也成立；当Ia+Ib+Ic≠0时必有一相接地，对地有有漏电流；对三相四线制则为Ia+Ib+Ic+Io=0成立，只要无漏电，三相分歧毛病称时也成立；因此，零序电流通常作为漏电故障判断的参数.负序电流则分歧，其主要应用于三相三线的电机回路；在没有漏电的情况下（即Ia+Ib+Ic=0），三相分歧毛病称时也会发作负序电流；负序电流常作为电机故障判断；注意了：Ia+Ib+Ic=0与三相对称不是一回事；Ia+Ib+Ic=0时，三相仍能够分歧毛病称.注意了：三相不服衡与零序电流不成混杂呀！三相不服衡时，纷歧定会有零序电流的；同样有零序电流时，三相仍能够为对称的.（这句话对吗?）前面好几位把两者混杂了吧！正序、负序、零序的呈现是为了剖析在系统电压、电流呈现分歧毛病称现象时，把三相的分歧毛病称重量分解成对称重量（正、负序）及同向的零序重量.只要是三相系统，一般针对三相三线制的电机回路，就能分解出上述三个重量（有点象力的分解与分解，但很多情况下某个重量的数值为零）.关于理想的电力系统，由于三相对称，因此负序和零序重量的数值都为零（这就是我们常说正常状态下只有正序重量的原因）.当系统呈现故障时，三相变得分歧毛病称了，这时就能分解出有幅值的负序和零序重量度了（有时只有其中的一种），因此通过检测这两个不应正常呈现的重量，就可以知到系统出了毛病（特别是单相接地时的零序重量）.下面再介绍用作图法复杂得出各重量幅值与相角的办法，先决条件是已知三相的电压或电流（矢量值），当然实际工程上是直接测各重量的.由于上不了图，请年夜家按文字说明在纸上画图.从已知条件画出系统三相电流（用电流为例，电压亦是一样）的向量图（为看很清楚，不要画成太极端）.总之，零序电流通常作为漏电故障判断的参数；负序电流常作为电机故障判断；正序电流对电机运行质量是一种评估.注意了：Ia+Ib+Ic=0与三相对称不是一回事；Ia+Ib+Ic=0时，三相仍能够分歧毛病称.三相不服衡与零序电流不成混杂呀！三相不服衡时，纷歧定会有零序电流的；同样有零序电流时，三相仍能够为对称的.两者不能混杂！三相四线电路中，三相电流的相量和等于零，即Ia+Ib+IC=0 如果在三相四线中接入一个电流互感器，这时感应电流为零.当电路中发作触电或漏电故障时，回路中有漏电电流流过，这时穿过互感器的三相电流相量和不等零，其相量和为：Ia+Ib+Ic=I(漏电电流）这样互感器二次线圈中就有一个感应电压，此电压加于检测局部的电子缩小电路，与呵护区装置预定举措电流值相比拟，如年夜于举措电流，即使灵敏继电器举措，作用于执行元件掉闸.这里所接的互感器称为零序电流互感器，三相电流的相量和不等于零，所发作的电流即为零序电流.发作零序电流的两个条件:1、无论是纵向故障、还是横向故障、还是正常时和异常时的分歧毛病称，只要有零序电压的发作；2、零序电流有通路.以上两个条件缺一不成.因为缺少第一个，就无源泉；缺少第二个，就是我们通常讨论的“有电压是否一定有电流的问题.零序公式:3U0=UA+UB+UC,3I0=IA+IB+IC弥补：正序、负序、零序的呈现是为了剖析在系统电压、电流呈现分歧毛病称现象时，把三相的分歧毛病称重量分解成对称重量（正、负序）及同向的零序重量.只要是三相系统，就能分解出上述三个重量（有点象力的分解与分解，但很多情况下某个重量的数值为零）.关于理想的电力系统，由于三相对称，因此负序和零序重量的数值都为零（这就是我们常说正常状态下只有正序重量的原因）.当系统呈现故障时，三相变得分歧毛病称了，这时就能分解出有幅值的负序和零序重量度了（有时只有其中的一种），因此通过检测这两个不应正常呈现的重量，就可以知到系统出了毛病（特别是单相接地时的零序重量）.三相电路分歧毛病称时，电流均可分解正序、负序和零序电流.正序指正常相序的三相交流电(即A、B、C三相空间差120度，相序为正常相序），负序指三相相序与正常相序相反（三相仍差120度，仍平衡），零序指（A、B、C电流分解出来三个年夜小相同、相位相同的相量.零序电流互感器套在三芯电缆上，三相不服衡时在外部就表现出零序电流（因为相量相同增强）正常电流（理想情况）：只有正序电流单相接地短路：故障相正序、负序、零序电流相等两相短路：故障点零序电流为零，正序和负序电流互为相反数两相短路接地：故障点正序、负序、零序电流均有三相对称短路：只有正序三相对称接地短路：有正序和零序三相分歧毛病称短路：有正序和负序三相分歧毛病称接地短路：有正序负序和零序一相断线：断口电流有正序、负序和零序两相断线：断口上各序电流相等上述观念仅作参考，欢送各位持续讨论！。

对称分量法（零序，正序，负序）的理解与计算1）求零序分量：把三个向量相加求和。

即A相不动，B相的原点平移到A相的顶端（箭头处），注意B相只是平移，不能转动。

同方法把C相的平移到B相的顶端。

此时作A相原点到C相顶端的向量（些时是箭头对箭头），这个向量就是三相向量之和。

最后取此向量幅值的三分一，这就是零序分量的幅值，方向与此向量是一样的。

2）求正序分量：对原来三相向量图先作下面的处理：A相的不动，B相逆时针转120度，C 相顺时针转120度，因此得到新的向量图。

按上述方法把此向量图三相相加及取三分一，这就得到正序的A相，用A相向量的幅值按相差120度的方法分别画出B、C两相。

这就得出了正序分量。

3）求负序分量：注意原向量图的处理方法与求正序时不一样。

A相的不动，B相顺时针转120度，C相逆时针转120度，因此得到新的向量图。

下面的方法就与正序时一样了。

对电机回路来说是三相三线线制，Ia+Ib+Ic=0，三相不对称时也成立；当Ia+Ib+Ic≠0时必有一相接地，对地有有漏电流；对三相四线制则为Ia+Ib+Ic+Io=0成立，只要无漏电，三相不对称时也成立；因此，零序电流通常作为漏电故障判断的参数。

负序电流则不同，其主要应用于三相三线的电机回路；在没有漏电的情况下（即Ia+Ib+Ic=0），三相不对称时也会产生负序电流；负序电流常作为电机故障判断；注意了：Ia+Ib+Ic=0与三相对称不是一回事；Ia+Ib+Ic=0时，三相仍可能不对称。

注意了：三相不平衡与零序电流不可混淆呀！三相不平衡时，不一定会有零序电流的；同样有零序电流时，三相仍可能为对称的。

（这句话对吗?）前面好几位把两者混淆了吧！正序、负序、零序的出现是为了分析在系统电压、电流出现不对称现象时，把三相的不对称分量分解成对称分量（正、负序）及同向的零序分量。

只要是三相系统，一般针对三相三线制的电机回路，就能分解出上述三个分量（有点象力的合成与分解，但很多情况下某个分量的数值为零）。

对称分量法正序：A相领先B相120度，B相领先C相120度，C相领先A相120度。

负序：A相落后B相120度，B相落后C相120度，C相落后A相120度。

零序：ABC三相相位相同，哪一相也不领先，也不落后。

三相短路故障和正常运行时，系统里面是正序。

单相接地故障时候，系统有正序、负序和零序分量。

两相短路故障时候，系统有正序和负序分量。

两相短路接地故障时，系统有正序、负序和零序分量称分量法基本概念和简单计算正常运行的电力系统，三相电压、三相电流均应基本为正相序，根据负荷情况（感性或容性），电压超前或滞后电流1个角度（Φ），如图1。

图1：正常运行的电力系统电压电流矢量图对称分量法是分析电力系统三相不平衡的有效方法，其基本思想是把三相不平衡的电流、电压分解成三组对称的正序相量、负序相量和零序相量，这样就可把电力系统不平衡的问题转化成平衡问题进行处理。

在三相电路中，对于任意一组不对称的三相相量（电压或电流），可以分解为3组三相对称的分量。

图2：正序相量、负序相量和零序相量（以电流为例）当选择A相作为基准相时，三相相量与其对称分量之间的关系（如电流）为：IA=Ia1+Ia2+Ia0――――――――――――――――――――――――――○1IB=Ib1+Ib2+Ib0=α2 Ia1+αIa2 + Ia0――――――――――○2IC=Ic1+Ic2+Ic0=α Ia1+α2 Ia2+Ia0―――――――――――○3对于正序分量：Ib1=α2 Ia1 ，Ic1=αIa1对于负序分量：Ib2=αIa2 ，Ic2=α2Ia2对于零序分量：Ia0= Ib0 = Ic0式中，α为运算子，α=1∠120°有α2＝1∠240°, α3＝1, α+α2+1=0由各相电流求电流序分量：I1=Ia1= 1/3(IA +αIB +α 2 IC)I2=Ia2= 1/3(IA +α2 IB +αIC)I0=Ia0= 1/3(IA +IB +IC)以上3个等式可以通过代数方法或物理意义（方法）求解。

对称分量法（零序，正序，负序)的理解与计算1）求零序分量：把三个向量相加求和。

即A相不动，B相的原点平移到A相的顶端（箭头处)，注意B相只是平移，不能转动。

同方法把C相的平移到B相的顶端。

此时作A相原点到C相顶端的向量(些时是箭头对箭头），这个向量就是三相向量之和.最后取此向量幅值的三分一，这就是零序分量的幅值,方向与此向量是一样的。

2）求正序分量：对原来三相向量图先作下面的处理：A相的不动,B相逆时针转120度，C 相顺时针转120度,因此得到新的向量图。

按上述方法把此向量图三相相加及取三分一，这就得到正序的A相，用A相向量的幅值按相差120度的方法分别画出B、C两相.这就得出了正序分量。

3）求负序分量：注意原向量图的处理方法与求正序时不一样。

A相的不动，B相顺时针转120度，C相逆时针转120度，因此得到新的向量图.下面的方法就与正序时一样了.对电机回路来说是三相三线线制，Ia+Ib+Ic=0，三相不对称时也成立；当Ia+Ib+Ic≠0时必有一相接地，对地有有漏电流；对三相四线制则为Ia+Ib+Ic+Io=0成立，只要无漏电，三相不对称时也成立；因此，零序电流通常作为漏电故障判断的参数。

负序电流则不同，其主要应用于三相三线的电机回路;在没有漏电的情况下（即Ia+Ib+Ic=0）,三相不对称时也会产生负序电流；负序电流常作为电机故障判断；注意了：Ia+Ib+Ic=0与三相对称不是一回事；Ia+Ib+Ic=0时，三相仍可能不对称。

注意了：三相不平衡与零序电流不可混淆呀！三相不平衡时，不一定会有零序电流的；同样有零序电流时，三相仍可能为对称的.（这句话对吗？）前面好几位把两者混淆了吧！正序、负序、零序的出现是为了分析在系统电压、电流出现不对称现象时，把三相的不对称分量分解成对称分量（正、负序)及同向的零序分量。

只要是三相系统，一般针对三相三线制的电机回路，就能分解出上述三个分量(有点象力的合成与分解，但很多情况下某个分量的数值为零）。

对称分量法公式【实用版】目录1.对称分量法公式的概念2.对称分量法公式的推导3.对称分量法公式的应用4.对称分量法公式的优点与局限性正文对称分量法公式是一种电气工程中常用的公式，主要用于三相电路的分析和计算。

它的基本思想是将三相电路中的三个独立电压或电流分解为三个对称分量的叠加，这样可以简化电路的分析过程。

下面将对称分量法公式的概念、推导、应用以及优点与局限性进行详细介绍。

1.对称分量法公式的概念对称分量法公式指的是将三相电路中的电压或电流分解为正序分量、负序分量和零序分量的叠加。

正序分量表示三相电压或电流的平衡部分，负序分量表示三相电压或电流的失衡部分，零序分量表示三相电压或电流的共模部分。

2.对称分量法公式的推导对称分量法公式的推导过程较为复杂，涉及到傅里叶级数和三角函数的运用。

简单来说，通过对三相电压或电流进行傅里叶变换，可以将其分解为三个独立的傅里叶级数，再通过三角函数的变换，可以将这三个傅里叶级数转化为正序分量、负序分量和零序分量。

3.对称分量法公式的应用对称分量法公式在电气工程中有广泛的应用，主要包括以下几个方面：（1）电力系统的故障分析：通过对称分量法公式，可以分析出电力系统中的各种故障，如相间短路、单相接地等。

（2）电力系统的保护设计：通过对称分量法公式，可以设计出各种保护装置，如过电流保护、过电压保护等。

（3）电力系统的控制策略：通过对称分量法公式，可以提出各种控制策略，如矢量控制、直接转矩控制等。

4.对称分量法公式的优点与局限性对称分量法公式的优点主要体现在以下几个方面：（1）简化电路分析：通过对称分量法公式，可以将复杂的三相电路简化为三个独立的单相电路，降低了分析难度。

（2）适用范围广泛：对称分量法公式适用于各种三相电路，无论是平衡电路还是不平衡电路，都可以使用对称分量法公式进行分析。

然而，对称分量法公式也存在一定的局限性：（1）对于非对称故障，对称分量法公式的计算结果会有误差。